基于模型预测控制的混合动力船舶能量控制策略
2018-07-04高迪驹张伟王旭阳潘海邦
高迪驹, 张伟, 王旭阳, 潘海邦
(上海海事大学航运技术与控制工程交通行业重点实验室,上海 201306)
0 引 言
为了改善船舶的燃油经济性,许多船舶开始采用混合动力系统[1-3]。混合动力船舶能量控制策略对提高混合动力系统燃油经济性十分关键,是一直以来研究的热点。常见的混合动力船舶的能量控制策略主要有:基于规则的控制策略(包括基于模糊逻辑和确定规则的控制策略)和基于优化理论的控制策略(包括基于全局优化和基于瞬时优化的控制策略),以及一些智能方法(如神经网络模型控制、基于遗传算法或最优控制算法的策略、动态规划等[4-6])。基于规则的控制策略不能应对混合动力船舶多种运行状况和实际船舶负荷需求的动态变化(即适应能力不足),不能达到最优控制;基于全局优化的控制策略适用范围存在局限性且计算复杂,因此很难应用到混合动力船舶的实际控制中;基于瞬时优化的控制策略不必事先获得船舶将来运行的工况数据,不受给定循环工况的约束,计算量小,容易实现。
常用的基于瞬时优化的控制策略有基于等效油耗最低(equivalent consumption minimization strategy, ECMS)和基于模型预测控制(model predictive control, MPC)的能量控制策略。基于ECMS的能量控制策略通常忽略动力电池组电荷状态(state of charge, SOC)的动态变化,是基于柴油机状况相同对动力电池组SOC进行补偿的策略,不能确保全局最优。基于MPC的能量控制策略在实时辨识船舶动态优化参数的基础上,将船舶燃油经济性的全局最优控制转变为预测情况下的局部最优控制,利用预测模型在预测时域内对船舶的需求功率进行预测,采用智能算法对混合动力船舶的柴油发电机组与锂电池组的功率分配比进行优化,获得混合动力船舶较高的燃油经济性;该策略具有基于模型的预测、滚动优化和反馈校正的特点,使得它可以更好地处理多目标、多约束、非线性等更复杂多变的问题,对混合动力船舶的能量控制优化具有很好的适用性[7-8]。当前国内外对基于MPC的能量控制策略的研究主要体现在混合动力汽车的能量管理策略上:文献[9]提出了基于马尔科夫链的混合动力汽车MPC;文献[10]提出了运用指数函数预测车轮扭矩的方法,并将MPC与动态规划算法相结合,建立了基于MPC且以油耗最少为目标进行滚动优化的控制策略;文献[11]将随机MPC与动态规划相结合,提出了基于MPC且以油耗最少为目标进行滚动优化的控制策略,在MATLAB/Simulink平台上搭建了仿真模型,并与逻辑门限控制策略进行对比仿真。目前国内将基于MPC的能量控制策略应用到混合动力船舶上的研究相对较少。
本文首先建立船舶混合动力系统结构和能源运行模式;然后介绍MPC的基本原理及其控制过程,采用马尔科夫模型对船舶的需求功率进行预测,结合动态规划算法,以油耗最少为目标对船舶油耗进行优化;最后根据仿真结果,与基于模糊逻辑控制策略的油耗作对比。
1 混合动力船舶动力系统模型
1.1 船舶混合动力系统结构
本文选择串联式混合动力系统开展对能量优化问题的研究,该系统结构见图1。两种动力源分别为柴油发电机组和动力电池组,前者产生的交流电通过AC/DC装置传输到直流母线,来自后者的直流电通过DC/DC装置传输到直流母线;再通过逆变器供电给推进电机,带动螺旋桨运转[12]。
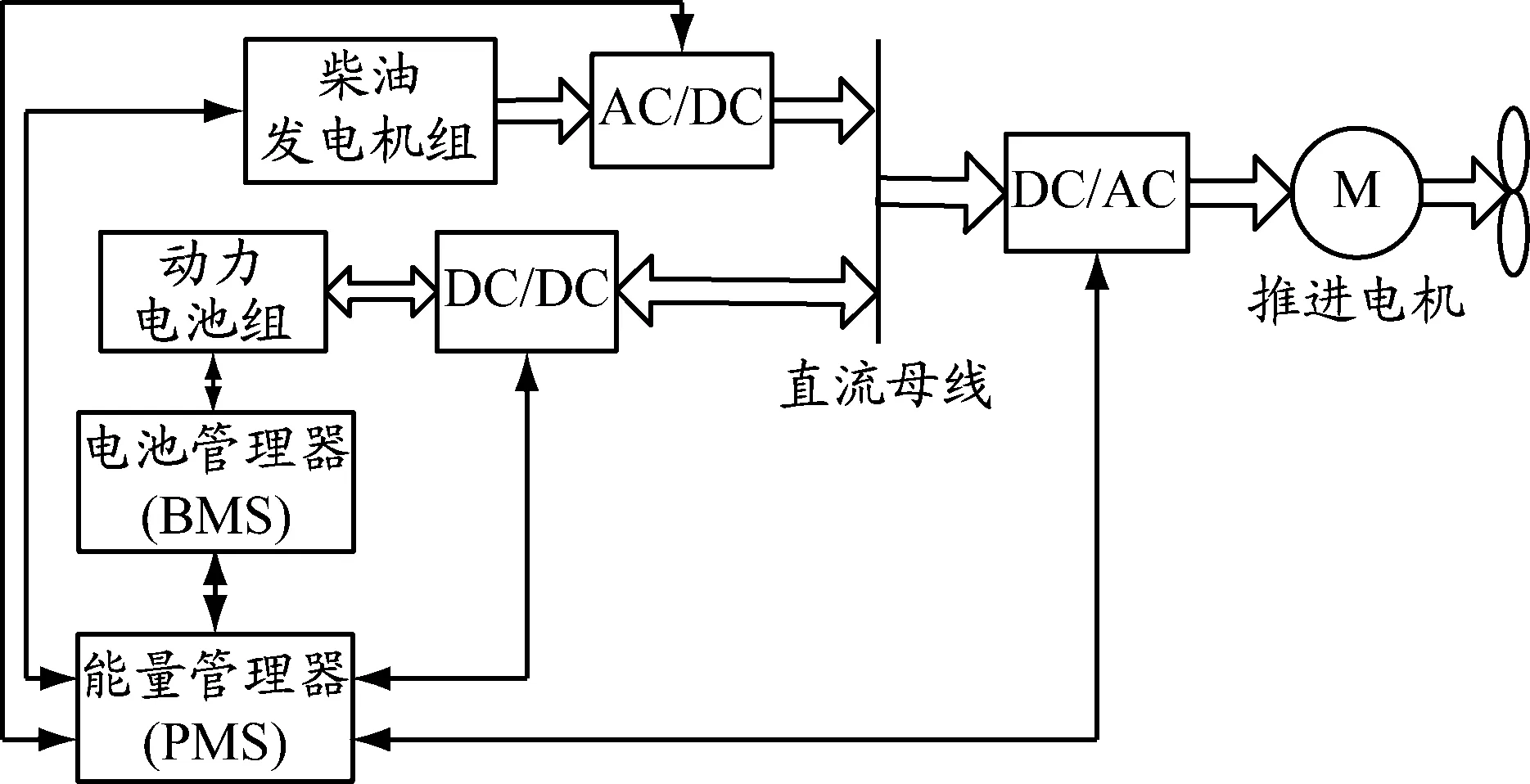
图1 船舶串联式混合动力系统结构
1.2 船舶混合动力系统能源运行模式
按照船舶运行工况下的功率需求,把串联式混合动力船舶的动力源优化组合为多种运行模式,通过切换到最优的运行模式来减少油耗。本文研究的串联式混合动力船舶能量管理系统包括动力电池组和柴油发电机组两种动力源,可根据能源使用情况将其运行模式分为3种:动力电池组单独供电模式、柴油发电机组单独供电模式和混合供电模式。不同运行模式下动力源输出功率与船舶需求功率的关系见表1。
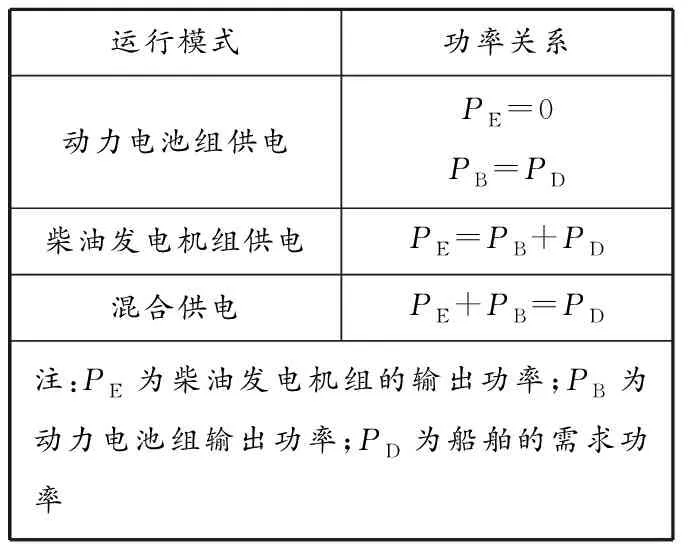
表1 船舶混合动力系统各运行模式下的功率关系
当动力电池组单独供电时,动力电池组单独工作来满足船舶负载功率需求,此时柴油机输出功率为0。当柴油发电机组单独供电时,柴油发电机组输出电能,再通过多路变换器为船舶推进电机提供电能和日常用电;此时柴油发电机组的输出功率PE大于推进电机的需求功率PD,剩余的功率则由动力电池组吸收为PB。在船舶负载功率需求较大或者动力电池组受温度影响较大等情况下需要柴油发电机组和动力电池组混合供电,维持船舶航行以及保证船舶日常用电。这种运行模式既能够保证船舶的动力需求,又可以达到减少油耗、减少排放的目标[13]。
2 基于MPC的功率分配
2.1 MPC原理
MPC可视为一种控制器,它将被控系统的当前状态作为初始状态,通过预测模型预测未来一段时间(预测时域)内的船舶需求功率,并通过优化算法得到该预测时域内的最佳柴油发电机组和动力电池组的功率分配控制序列,然后将其第一组柴油发电机组和动力电池组功率分配值用于船舶,在下一时刻重复上述过程。MPC的基本原理可以归结为模型预测、滚动优化(区别于传统最优控制的根本点)和反馈校正等3个主要部分,其原理[14]见图2。

图2 MPC原理
2.2 需求功率预测模型的建立
将基于MPC的能量控制策略运用到船舶能量控制优化中,首先要寻找合适的预测模型对船舶未来需求功率进行预测。本研究利用马尔科夫模型对船舶未来需求功率进行预测;将船舶的未来需求功率看作是一种概率分布,建立随机马尔科夫模型,而船舶未来需求功率值的概率分布可以从以往的航行数据中总结得出。将需求功率离散为有限数值,令T为船舶需求功率的集合,则定义T={z1,z2,…,zs},混合动力船舶需求功率预测模型由转移概率矩阵PM定义:
tab=P[τ(k+i+1)=b|τ(k+i)=a],
tab∈R
式中:tab是转移概率矩阵PM的第a行第b列元素,a,b∈T;P[τ(k+i+1)=b|τ(k+i)=a]表示k+i时刻的船舶需求功率a在k+i+1时刻变化到b的概率。
预测船舶需求功率,即描述转移概率矩阵PM。转移概率可以从以往的航行记录中提取归纳,令P(k+i)=(Pz1(k+i),Pz2(k+i),…,Pzs(k+i)),式中:Pzi(k+i)表示在k+i时刻船舶需求功率值为zi的概率。可以得出下列关系式:
P(k+n-1)=P(k+n-2)PM=P(k)(PM)n-1
由于在k时刻船舶需求功率值τ(k)已知,所以P(k)已知。利用上述公式可以求出船舶需求功率在预测时域内各预测点处的分布概率。最后选取各预测点k+i处概率最大的需求功率值作为该时刻预测的船舶需求功率值,至此完成马尔科夫预测模型的建立。
2.3 目标函数及约束
基于MPC的能量控制优化的目标是:在预测时域内使混合动力系统的总油耗最少。总油耗包括柴油发电机组的油耗和电池组电量的等效油耗。定义系统阶段指标函数是在k时刻的总油耗:
Fk=FEk+FBk
(1)
(2)
式中:Fk为k时刻总的等效油耗;FEk为k时刻柴油发电机组的油耗;FBk为k时刻电池组电量的等效油耗;PEk和PBk分别为柴油发电机组和动力电池组在k时刻的输出功率;q为柴油发动机组油耗率;Tec为柴油发动机冷却水温;S为等效油电平均转换效率;e通常取3.1;ηchg和ηdis分别为电池的充电、放电效率;ηm为等效推进电机的平均效率;ηe为等效柴油发动机平均效率;H为等效燃油的低热值;ηq为等效油电转换支路的机械传动效率平均值。系统在预测时域t内的总油耗为
因此,系统目标函数就是系统在预测时域内的总油耗最少,即
基本约束条件如下:
(1)柴油发电机组的输出功率限制:
式中:PE min和PE max分别为柴油发电机组的最小和最大输出功率。
(2)电池组充放电功率和SOC值限制。电池组充放电功率限制如下:
-Pchg max≤PBk≤Pdis max
式中:Pchg max和Pdis max分别为电池组最大充电功率和最大放电功率。动力电池组SOC值限制如下:在k时刻动力电池组的SOC值要介于电池组的最小与最大电荷值之间。
(3)负载需求功率响应条件。为确保混合动力船舶完成工作任务,负载需求功率响应的约束条件可以写成:
PEk+PBk≥PDk
式中:PDk为船舶在k时刻的负载需求功率。
2.4 目标函数的求解
本文采用贝尔曼动态规划的方法在有限时域内对油耗最少目标函数进行求解。选取电池组的SOC值作为系统状态量,这是因为其基本可以反映出各个时刻系统的能量状态。将动态规划过程分为n个时段进行求解,步骤为:(1)将SOC在允许的范围内进行离散化;(2)逆向求解每个时段、每个SOC离散点的最优控制量;(3)正向寻找各个时段的最优控制量。这里,逆向求解过程描述如下:
第n-1个时段:
第k个时段(1≤k≤n-2):

首先采用从第n个时段开始直到第1个时段结束的逆向求解方式,计算各阶段每个SOC离散值上的最优解及从该时段到第n个时段的最小代价函数,在后面的正向寻优过程中会用到。
给定初始SOC值后,采用正向寻优的方式确定最佳控制路径。从第1个时段开始,已知当前时段的SOC值,从之前逆向求解的结果中寻找到该时段、该状态下的最优控制量,并将该最优控制量作为当前时段的控制量发送给船舶,计算下一时段的SOC值,进入下一时段寻优过程;依此类推,直到n-1个时段正向寻优过程结束。
正向计算完成后,整个动态规划过程结束,这样即可获得整个过程的最优控制序列及电池组SOC值变化轨迹[15]。
2.5 基于MPC的能量控制流程
基于MPC的能量控制策略基本步骤[16]可以归纳如下:
①获取当前时刻(k时刻)的混合动力船舶的负载需求功率和电池组的SOC值。
②在当前时刻根据马尔科夫预测模型预测在k到k+t时域内的船舶负载需求功率,每隔时间Δt预测一次,其中Δt与控制周期相同。
③用动态规划算法计算目标函数在预测时域内的最优值,由此得到在k到k+t时域内的柴油发电机组和动力电池组的最佳功率分配解集。
④将第3步计算得出的最佳功率分配解集中的第1组柴油发电机组功率和动力电池组功率作为控制变量发送给相应控制器。
⑤在下一个控制循环过程中,重复以上步骤向前优化。
由上述步骤可以看出,基于MPC的能量控制策略结合动态规划算法的最优控制策略在k时刻仅计算k到k+t时域内的柴油发电机组和动力电池组的最佳功率分配序列,到k+1时刻同样只计算k+1到k+1+t时域内的柴油发电机组和动力电池组的功率分配解集,如此向前滚动优化。这样可以使得每次计算区域远小于整个航行区域,大大降低了动态规划的计算量,提高了效率。
3 试验与分析
之前的航行数据是通过混合动力船舶试验平台获得的,该试验平台配备了16组总容量为100 A·h的动力性磷酸铁锂电池、2组额定功率为30 kW的柴油发电机、2组额定输出功率为35 kW的推进电机。船舶参数为:排水量92 t,阻力因数694.2,螺旋桨直径0.8 m,螺旋桨转速1 500 r/min。
此外,为验证MPC优化策略的控制效果,将其与基于模糊逻辑控制策略的油耗进行对比研究,模糊逻辑控制策略是在逻辑门限策略的基础上,采用与模糊逻辑算法相结合的改进策略作为控制策略的,通过机桨模型预测得出下一时刻推进电机的需求功率PD,其与当前推进电机测得的实际功率PR之差ΔP和电池组SOC值进行模糊化处理后作为模糊控制器的输入,通过模糊运算得出柴油发电机组的功率调节因数α,再根据推进电机功率计算模块得出发电机组在下一时刻的输出功率,进而通过需求功率与发电机组输出功率之差得出电池组的输出功率,对电池组的充放电状态进行控制,从而调节电池组的SOC值[17],得到电池组和柴油发电机组的功率分配。可通过上述功率与油耗的关系式得出预测时域内的油耗,采用模糊逻辑控制策略在一定程度上可以减少油耗和排放。
在仿真中,船舶在整个航行周期中的运行工况包括启动、加速、全速前进、减速和停止。采用的预测时域为3 s,控制周期为60 ms,即预测50个状态点,n=50。图3是在两种控制策略下整个仿真过程的SOC值变化曲线。图4是在两种控制策略下发电机组油耗对比,其中:MPC策略是在一个预测时域3 s内,每隔60 ms用马尔科夫模型预测一次船舶负载需求功率(即在一个预测时域内预测50个状态点,取前一时刻的预测值作为下一个时刻的负载需求功率)。将得到的负载需求功率在预测时域内用动态规划的方法计算最优值(即得到柴油发电机组和电池组的功率解集)。运用式(1)可得到各个时刻的柴油发电机组油耗随时间变化的曲线,基于模糊逻辑控制策略的油耗曲线也是根据上述基于模糊逻辑控制策略的功率解集计算得到的。图5为在两种控制策略下电池组等效油耗随时间变化的曲线,是通过以上方法得到电池组功率分配,进而通过式(2)计算得出的。经研究,仿真结果与理论分析较吻合。

图3 SOC值变化对比
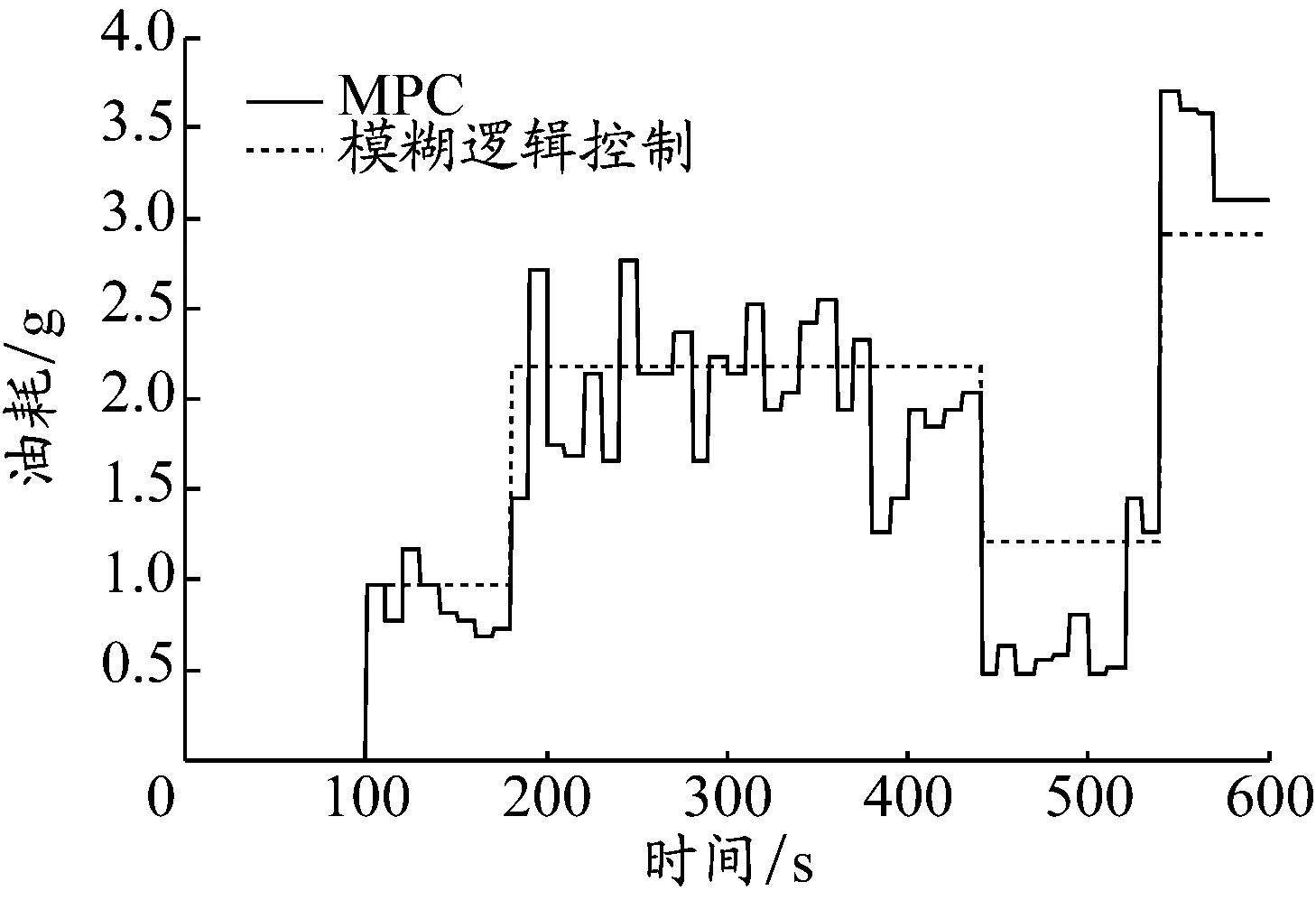
图4 发电机组油耗对比
用MATLAB/Simulink对两种控制策略进行仿真的结果见表2。
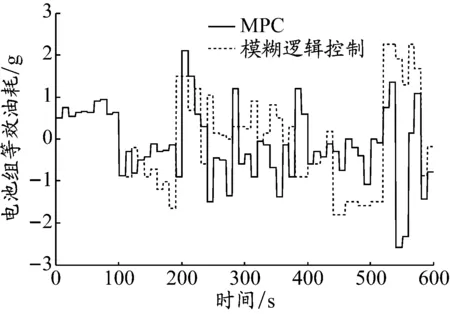
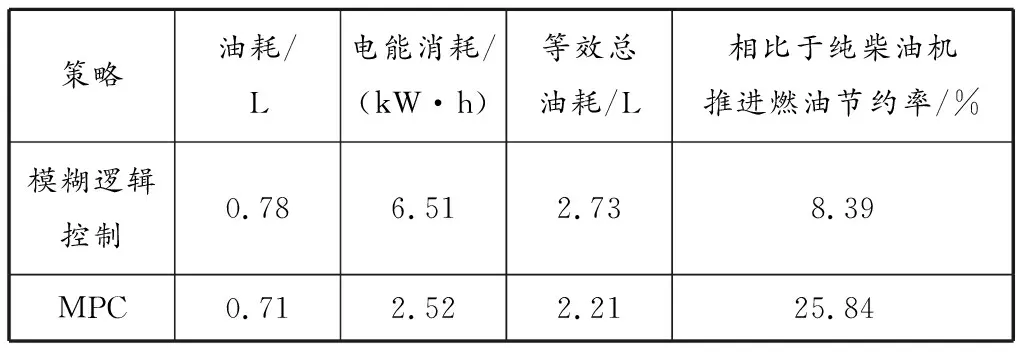
图5 电池组等效油耗对比表2 两种策略仿真结果对比
策略油耗/L电能消耗/(kW·h)等效总油耗/L相比于纯柴油机推进燃油节约率/%模糊逻辑控制0.786.512.738.39MPC0.712.522.2125.84
从图3中可以看出,基于模糊逻辑控制策略的电池组电量波动幅度较大,且在整个试验周期中动力电池组电量消耗较大,SOC末值比初值减少了18%,表明模糊逻辑控制策略比MPC策略更多地采用了电力驱动。再将图3与图4和5结合起来看,在启动过程中SOC曲线下降很快,发动机的油耗几乎为0,说明在此过程中船舶的功率需求基本是由电池组满足的。从表2的电能消耗看,整个试验周期中采用模糊逻辑控制策略比采用MPC策略的电能消耗多出3.99 kW·h。从图4可以看出,基于模糊逻辑控制策略的油耗略大于基于MPC策略的油耗。从表2可以看出整个试验周期内采用MPC的策略能节约油耗0.07 L。图5中纵坐标为负数表示电池吸收能量,不提供动力,此时柴油发电机组提供的功率一部分驱动船舶航行,一部分给电池充电,这种情况下等效的总油耗即为发动机的油耗。在整个试验周期内,基于MPC策略比基于模糊逻辑控制策略的等效油耗节约了0.99 L,燃油经济性有明显提高。此外,从表2中还可以看出,混合动力船舶比纯柴油机驱动的船舶油耗明显减少,基于MPC策略和基于模糊逻辑控制策略的混合动力船舶比纯柴油机驱动的船舶燃油经济性分别提高了25.84%和8.39%。对比两种控制策略,在此仿真测试工况下,基于MPC策略比基于模糊逻辑控制策略的燃油经济性也提高了19.05%。
4 结束语
本文将模型预测控制(MPC)算法应用到混合动力船舶能量控制优化过程中,提出了一种基于马尔科夫链的预测模型对船舶未来负载功率进行预测,并用动态规划的方法计算得到柴油发电机组与动力电池组的最佳功率分配。由试验结果对比可以看出,采用MPC策略能够在一定程度上提升混合动力船舶的燃油经济性,具有一定实际工程的应用开发前景。
参考文献:
[1] FERRY M, WB W N, MFAHMAD,etal. Comparative study of hybrid catamaran versus diesel monohull boat as ferry for short distance routes[J]. Indonesian Journal of Naval Architecture, 2013, 1(1): 30-36.
[2] WIEDEBACK N J, JOHNSON B K, HESS H L,etal. A PSCAD/EMTDC model of a marine vehicle propulsion system[C]//IEEE Transmission and Distribution Conference and Exposition (T & D), IEEE, 2012: 1-8.
[3] 俞万能, 李丹, 郑为民. 太阳能游览船能量控制系统研发[J]. 中国造船, 2013, 54(3): 177-183.
[4] BERNARD J, DELPRAT S, GUERRA T M,etal. Fuel efficient power management strategy for fuel cell hybrid powertrains[J]. Control Engineering Practice, 2010, 18(4): 408-417.
[5] KANELLOS F D, TSEKOURAS G J, HATZIARGYRIOU N D. Optimal demand-side management and power generation scheduling in an all-electric ship[J]. IEEE Transactions on Sustainable Energy, 2014, 5(4): 1166-1175. DOI: 10.1109/TSTE.2014.2336973.
[6] TANI A,CAMARA M B, DAKYO B. Energy management in the decentralized generation systems based on renewable energy-ultracapacitors and battery to compensate the wind/load power fluctuations[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1817-1827. DOI: 10.1109/TIA.2014.2354737.
[7] 赵秀春, 郭戈. 混合动力电动汽车能量管理策略研究综述[J]. 自动化学报, 2016, 42(3): 321-334. DOI: 10.16383/j.aas.2016.c150477.
[8] 李书臣, 徐心和, 李平. 预测控制最新算法综述[J]. 系统仿真学报, 2004, 16(6): 1314-1319.
[9] 孟凡博, 黄开胜, 曾祥瑞, 等. 基于马尔科夫链的混合动力汽车模型预测控制[J]. 中国机械工程, 2014, 25(19): 2692-2697. DOI: 10.3969/j.issn.1004—132X.2014.19.025.
[10] 赵韩, 吴迪. ISG混合动力汽车模型预测控制策略研究[J]. 合肥工业大学学报(自然科学版), 2014, 37(1): 1-5. DOI: 10.3969/j.issn.1003-5060.2014.01.001.
[11] 赵韩, 吴迪. 基于随机模型预测控制的并联式混合动力汽车控制策略研究[J]. 汽车工程, 2014, 36(11): 1289-1294.
[12] 魏伟, 褚建新, 王帆. 串联式混合动力船舶能源系统运行模式切换策略[J]. 船舶工程, 2016, 38(4): 26-30. DOI: 10.13788/j.cnki.cbgc.2016.04.026.
[13] 高迪驹, 沈爱弟, 褚建新, 等. 混合动力船舶的能量管理与控制策略[J]. 上海海事大学学报, 2015, 36(1): 70-74. DOI: 10.13340/j.jsmu.2015.01.013
[14] 樊娟娟. 基于预测控制的并联式混合动力汽车能量管理策略研究[D]. 济南: 山东大学, 2012.
[15] 张洁丽. 基于模型预测控制的插电式混合动力客车能量管理策略研究[D]. 北京: 北京理工大学, 2016.
[16] 曾祥瑞, 黄开胜, 孟凡博. 具有实时运算潜力的并联混合动力汽车模型预测控制[J]. 汽车安全与节能学报, 2012, 3(2): 165-172. DOI: 10.3969/j.issn.1676-8484.2012.02.010.
[17] 孙彦琰, 高迪驹, 褚建新. 混合动力电动船舶模糊逻辑控制策略[J]. 船舶工程, 2014, 36(3): 67-70. DOI: 10.13788/j.cnki.cbgc.2014.0079.
