低碳环境下电动汽车车辆路径问题

梁凤婷， 胡坚堃， 黄有方

(上海海事大学物流科学与工程研究院， 上海 201306)

0 引 言

交通运输业的快速发展带来了严重的环境问题和能源问题。为解决这些问题，世界各国都开始发展 “低碳经济”，以实现经济和社会的可持续发展。在“低碳经济”理论指导下的新能源汽车转型已成为我国低碳城市建设的重要工作之一[1]。与传统燃油汽车相比，电动汽车具有能耗低、污染小以及国家政策支持的优势，并且随着电池和充电技术的快速发展，其逐步成为物流领域重要的新能源交通工具。自2009年起，我国政府相继颁布了《电动汽车科技发展“十二五”专项计划》《节能与新能源汽车产业发展规划(2012—2020年)》等，以促进电动汽车的普及和应用。

为响应国家政策的号召以及减少企业成本，许多企业经营者和学者对低碳环境下燃油汽车和电动汽车的车辆路径问题(vehicle routing problem, VRP)进行研究，以减少碳排放量和降低运输成本。MOLINA等[2]基于契比雪夫方法提出了关于异质车辆的多目标VRP模型，以期在降低内部成本的同时减少CO2和空气污染物的排放，并且设计了与模型对应的C&W节约算法求解模型，最后通过实例验证了模型和算法的实用性。ZHANG等[3]将碳排放成本和燃油成本加入到传统的配送路径优化模型中，采用禁忌搜索算法获得了较优的解，但没有考虑车辆装载量和车速变化对碳排放的影响。钟聪儿等[4]通过将碳排放货币化，建立了综合考虑碳排放和运输费用的配送路径优化模型，并通过遗传算法进行求解，结果表明在传统运输路径中存在很大的碳排放改善空间。张如云等[5]提出了综合考虑低碳、节能和节约成本的城市车辆配送问题(emission-time dependent vehicle routing problem，E-TDVRP)模型，并使用基于客户实数编码方式的改进遗传算法对模型进行求解，但没有考虑车辆装载量的影响。LIN等[6]综合考虑时间成本、燃料成本以及电动汽车数量，提出了电动汽车路径问题(electric vehicle routing problem，EVRP)的通用模型，并通过实例分析发现，电动汽车的燃料成本低，但是其时间成本较大导致其总成本高于传统燃油汽车的总成本。FELIPE等[7]通过考虑部分再充电和多种充电技术，将原来的GVRP(green VRP)模型拓展为GVRP-MTPR(GVRP with multiple technologies and partial recharges)模型，并提出了与本地搜索相结合的启发式算法对模型进行求解。AFRODITI等[8]提出了含有时间窗的EVRP模型，但是无法直接观察到电动汽车对经济和环境的影响。杨珺等[9]针对电动汽车的换电站选址和配送路径优化问题，建立了相应的整数规划模型，并设计了基于禁忌搜索和改进的C&W节约算法的两阶段启发式算法求解模型，发现总成本随着装载量和电池续航里程的增加而显著降低。揭婉晨等[10]针对含有时间窗的EVRP，建立了相应的混合整数规划模型，通过设计基于列生成的分支定价算法求解，并使用CPLEX对模型和算法结果的准确性进行了验证。

当前国内针对电动汽车的研究还比较少，在已有的研究中很少考虑车辆能源消耗问题和能源转化率问题，在燃油汽车与电动汽车的对比研究中也很少将车辆的经济性与节能减排的效果结合起来分析。目前电动汽车的续航能力大多在100～200 km[10]，无法满足里程要求，需要在配送过程中进行充电，这导致配送里程和时间成本增加。针对以上问题，本文在考虑车辆能源转化率的基础上，分别建立低碳环境下传统汽油车VRP模型和EVRP模型，将企业的经济效益与环境效益结合起来，以包含时间成本、燃料成本和碳排放成本的总成本最小为目标函数。通过实例分别求得两种模型下的最小总成本和碳排放量，并对结果进行比较分析，同时对电池容量、充电时间、电费进行灵敏度分析，了解其变化对电动汽车配送成本和碳排放量的影响，以期为未来物流企业车辆转型政策的制定提供理论依据。

1 问题描述

本文考虑由一个配送中心向多个客户进行配送的情况，配送中心拥有足够数量的同质车辆。当有运输任务时，车辆从配送中心出发，完成任务后返回配送中心。在传统的VRP网络中，网络节点集是所有客户节点和配送中心的集合，其中所有客户节点都要被访问且只能被访问一次，而在EVRP网络中还要包含所有的充电站节点。要求配送中心合理设计每辆车的运输任务以及相应的路线，降低运输过程中产生的时间成本、燃料成本以及碳排放成本，使得运输总成本最低、经济效益最大。

集合和参数：N为所有节点的集合，N={1,2…,n}，其中1为配送中心;N0为所有客户节点的集合，N0={2,3,…,m}；N′为除配送中心外所有节点的集合，N′={2,3,…,n}，在传统燃油汽车的路径模型中N′=N0；C为所有充电站的集合，C={m+1,m+2,…,n} ；K为配送中心所有车辆的集合，K={1,2,…,M} ；s为司机工资，元/h；dij为节点i与j之间的距离，km；cf为单位体积的燃料成本(算例中采用93#汽油价格)，元/L；ce为单位质量的CO2成本(算例中采用碳排放交易价格)，元/kg；ct为单位电耗成本，元/(kW·h)；H为车辆每天的最长工作时间，h；Q为车辆的载质量，kg；E为电动汽车的电池容量，kW·h；v为车辆的行驶速度，km/h；qi为客户节点i的需求，kg，∀i∈N0；qr为客户节点r的需求，kg，∀i∈N0；p为电池的充电率，为一常数；ρ*和ρ0分别为传统汽油车满载和空载时的油耗率，L/km。

决策变量：xijk为0-1变量，若车辆k从节点i行驶到节点j则为1，否则为0；xrik为0-1变量，若车辆k从节点r行驶到节点i则为1，否则为0；xirk为0-1变量，若车辆k从节点i行驶到节点r则为1，否则为0；xrjk为0-1变量，若车辆k从节点r行驶到节点j则为1，否则为0；lij为节点i与j之间的装载量，kg；lir为节点i与r之间的装载量，kg；lrj为节点r与节点j之间的装载量，kg；tij为节点i与j之间的行驶时间，h；ρij为节点i与j之间的油耗率，L/km；δij为节点i与j之间的单位距离耗电量，kW·h/km；τij为车辆从与节点j相连的节点i出发的时刻；τjr为车辆从与节点r相连的节点j出发的时刻；eik为车辆k在节点i的剩余电量，kW·h；ejk为车辆k在节点j的剩余电量，kW·h。

2 模型构建

本文综合考虑物流运输中的经济效益和环境效益，将追求低成本的经济目标与降低碳排放的社会责任结合起来，以时间成本、燃料成本和碳排放成本之和最小为目标函数，分别求出低碳环境下传统汽油车VRP模型和EVRP模型的最优成本和最佳路径安排。由于当前电池技术的限制，电动汽车存在行驶里程较短的问题，需要在配送过程中充电以增加行驶里程。本文采用基于社会充电网络的EVRP模型，并假设社会充电网络已经建设完善。此外，电动汽车虽然在运输过程中不会产生碳排放，但由于其使用电能，而中国当前以火力发电为主，所以EVRP模型中仍要考虑电力生产过程中的碳排放。本文碳排放成本以征收碳税的方法计算。

2.1 低碳环境下传统汽油车VRP模型

为便于分析和求解，对模型进行假设和简化。假设1：所有节点的位置以及客户需求量已知，且每个客户只能被同一辆车访问一次。假设2：所有车辆以某一恒定速度匀速行驶。假设3：车辆为同质车，且车辆数量已知。假设4：车辆每天的工作时间为8 h。假设5：车辆从配送中心出发，并最终回到配送中心。假设6：不考虑卸货和退货。假设7：车辆在每两个节点之间的路径上没有停留。假设8：不考虑客户服务的时间窗约束。假设9：每辆车只使用一次。假设10：只考虑装载量和里程对车辆的油耗率和碳排放的影响。

模型的目标函数(包括时间成本、燃料成本和碳排放成本)为

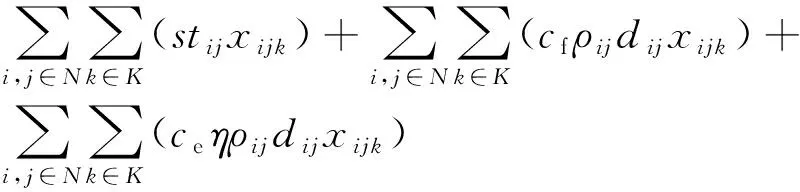
(1)

式中：η为碳排放量与油耗之间的换算系数；ρij的计算公式[11]为

ρij=(ρ0+(ρ*-ρ0)lij/Q)/ζ1

(2)

其中ζ1为传统汽油车的能源转化效率。

模型的约束条件为

式(3)表示所有配送车辆的起点和终点都是配送中心；式(4)表示所有客户的需求都要被满足，并且每个客户只能被一辆车服务一次；式(5)表示到达某个客户节点的车辆必须从该节点离开；式(6)表示每条配送路线上所有客户的总需求不超过车辆的载质量；式(7)表示每个客户的需求量等于在前一节点出发时的装载量减去在当前节点出发时的装载量；式(8)表示在每一节点的出发时刻等于在上一节点的出发时刻加上在两节点间行驶时间；式(9)表示车辆行驶时间应小于等于车辆工作时间；式(10)～(13)为参数与变量的取值约束。

2.2 EVRP模型

本文使用的模型是根据LIN等[6]提出的通用EVRP模型拓展而来的。前提假设除包含低碳环境下传统汽油车VRP模型中的假设1、 2、 4、 5、 7、 8和9外，还有：充电站已经建设完成，配送中心也为充电站之一，同一个充电站可以同时给多辆车充电，同一辆车可以在同一个充电站多次充电；电池的充电率是常量，电池离开每一个充电站时的电量是满的；车辆的单位距离耗电量仅考虑装载量的影响。

模型的目标函数(包括时间成本、燃料成本和碳排放成本)为

(14)

式中：λ为碳排放量与电耗之间的换算系数；参考文献[12]，可得

δij=(αij(w+lij)+βv2)/ζ2

(15)

其中:αij=a+gsinθij+gCrcosθij;β=0.5CdAρ;ζ2为电动汽车的能源转化效率;w为电动汽车的整备质量。这里,a为加速度，g为重力加速度，θij为道路角度，Cr为无单位滚动阻力，Cd为无阻抗系数滚动阻力，A为车辆的正表面积，ρ为空气密度。

模型的约束条件为

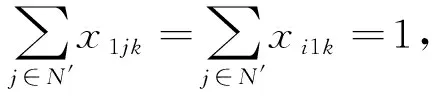
(16)

(17)

(18)

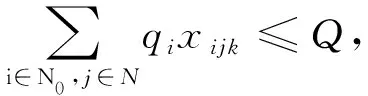
(19)

(20)

H(xijk-1)≤τij+tij-τjr≤H(1-xijk),

∀r,i∈N;j∈N0;k∈K

(21)

H(1-xijk),∀r,i∈N;j∈C;k∈K

(22)

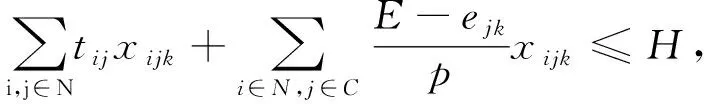
(23)

E(xijk-1)≤eik-ejk-δijdij≤E(1-xijk),

∀i∈N;j∈N;k∈K

(24)

E(xijk-1)≤E-ejk-δijdij≤E(1-xijk),

∀i∈C∪{0};j∈N0;k∈K

(25)

eik-δijdij≥0, ∀i∈N0;j∈C;k∈K

(26)

dij=vtij, ∀i,j∈N

(27)

0≤lij≤Q, ∀i,j∈N

(28)

0≤eik≤E, ∀i∈N;k∈K

(29)

0≤qi≤Q, ∀i∈N0

(30)

τ1j=0, ∀i∈N′

(31)

xijk∈{0,1}, ∀i,j∈N;k∈K

(32)

式(16)表示所有配送车辆的起点和终点都是配送中心；式(17)表示所有的客户需求都要被满足，并且每个客户只能被一辆车服务一次；式(18)表示到达某个节点的车辆必须从该节点离开；式(19)表示每条配送路径上所有客户的总需求不超过车辆的载质量；式(20)表示每个客户的需求量等于从前一节点出发时的装载量减去从当前节点出发时的装载量；式(21)和(22)分别表示从客户节点和充电站节点出发的时刻等于从上一节点出发的时刻加上在两节点间行驶的时间；式(23)表示车辆行驶时间加上总充电时间不超过每天的工作时间；式(24)和(25)表示每个节点上汽车的剩余电量等于从前一节点出发时的剩余电量减去在两节点之间消耗的电量，且从充电站出发时电量是满的；式(26)表示剩余电量应足够使汽车到达最近的充电站；式(27)～(32)为参数与变量的取值约束。

2.3 遗传算法设计

本文研究的重点在于构建EVRP模型，并与传统汽油车VRP模型的优化结果进行对比。由于遗传算法具有很强的全局寻优能力和实用性，能够满足本文模型求解和结果比较的需要，所以本文采用遗传算法对提出的EVRP模型和传统汽油车VRP模型进行求解，并对结果进行比较分析。算法步骤如下：

步骤1编码。采用自然数编码方式，对于有n个节点、M辆运输车的VRP，染色体的长度为n+M，则一个由1，2，…，n+M-2构成的随机排列和2个配送中心节点编号组成的序列即为一条合法的染色体。例如对于有10个节点、2辆运输车的VRP，(1 5 4 7 1 3 6 8 10 2 9 1)就是一条合法的染色体，其中1代表配送中心。

步骤2种群初始化。随机产生长度为n+M-2的随机排列，将其中大于n的数字转化为车辆分隔点1，分隔点前后的节点由不同的车辆配送[5]。最后在序列的最前端和最后端补上1[13]，就构成了一条初始染色体。如此重复，直到满足种群规模。对于EVRP模型，在产生一条染色体后，要从第一个节点开始计算消耗的电量之和，当到达节点i时，若剩余电量无法让运输车到达下一个节点或者无法从下一个节点到达最近的充电站，则要在节点i后面插入与此节点最近的充电站编号，如此反复直到循环到最后一个节点。

步骤3适应度函数确定。一般根据具体问题来确定适应度函数，本文采用目标函数的倒数作为适应度函数。考虑车辆载质量限制，在计算目标值时，采用惩罚函数对其加以约束，将车辆载质量约束作为目标函数的一部分[13]。

步骤4选择操作。采用随机遍历抽样方式进行个体选择。根据计算出的适应度值，求出每个个体被选择的概率(个体适应度值与适应度值之和的比值)，然后产生一个0与1之间的随机数，若个体被选择的概率大于这个随机数，则个体就被选择。这种方式能够保证最优个体进入下一代，并且适应度值越大的个体被选择的概率越大。

步骤5交叉操作。采用部分映射杂交的方式进行交叉操作。先确定交叉的父代，再随机生成交叉点，之后将两个父代进行交叉。交叉完成后，新生成的子代中可能出现重复的节点编号，对于有冲突的编号采用部分映射的方法消除冲突[14]。

步骤6变异操作。进行变异操作时，首先产生两个随机自然数确定变异的位置，选择位置所对应的节点编号进行交换。

步骤7进化逆转操作。为提高遗传算法的局部搜索能力，在遗传操作完成后进行进化逆转操作。首先产生两个随机整数确定两个位置，然后将这两个位置之间的所有节点编号进行逆转，例如个体A=(1 5 2 3 7 4 6 1)，产生的随机整数为4和6，则逆转后的个体为A=(1 5 2 4 7 3 6 1)。[14]只有适应度值提高的逆转操作才是有效的。之后进入下一代操作，直至满足设定的最大遗传代数。

3 算例实现

3.1 参数设置

本文所使用的需求节点的坐标来源于文献[13]，所选用的车辆为雷诺KANGOO Van和KANGOO Z E[15]，两种车型具有相同的规格，车辆的载质量为650 kg，客户的需求服从车辆载质量的10%和15%的均匀分布，车辆行驶速度为40 km/h，电动汽车的充电时间为1.5 h，司机工资为25元/ h。其他参数的值见表1。

表1 电动汽车各参数取值

3.2 运算结果及分析

采用遗传算法分别对传统汽油车VRP模型和EVRP模型进行求解。设置算法的迭代次数为1 000，种群规模为100，交叉概率为0.9，变异概率为0.05。分别运算30次后，各取目标值最小的结果作为两种模型下对应的最优解以及最优路径，见表2和3。

根据计算结果可以得到如下结论：

表2 传统汽油车VRP模型的优化结果

表3 EVRP模型的优化结果

(1)电动汽车配送的总成本和碳排放量均低于传统汽油车配送的总成本和碳排放量。电动汽车相对于传统汽油车，虽然行驶里程增加了9.12%，但成本降低了29.32%，碳排放量减少了32.22%。

(2)使用电动汽车不仅可以降低运输成本，还可以减少能源消耗，但要额外考虑时间成本。从成本的构成看:在传统汽油车VRP模型中，能源成本大于时间成本;在EVRP模型中，时间成本远大于能源成本，碳排放成本在两种模型中所占的比例都比较小。与传统汽油车VRP模型相比，EVRP模型中的能源成本降低了80.40%，但时间成本增加了37.18%。电动汽车的充电次数和时间，主要受电池容量和充电时间的影响，由于当前电池和充电技术的限制，充电时间过长，电动汽车的时间成本过高。

综上可知，在发展低碳物流的过程中，企业使用纯电动汽车，不仅可以降低配送成本，而且可以减少环境污染，降低能源消耗，并且随着技术的发展，电动汽车的运输成本将会进一步降低。

3.3 灵敏度分析

通过以上分析可以发现，电动汽车配送成本主要由时间成本和能源成本构成，影响时间成本的因素主要有电池容量和充电时间，影响能源成本的因素有能源价格(电费)，这3个因素的变化会直接影响本文模型的计算结果。因此，有必要对这3个因素进行灵敏度分析，分别求出各因素取不同值时的配送成本和碳排放量。计算结果见表4。

表4 各因素变化对配送成本和碳排放量的影响

从表4可以看出:随着充电时间的减少、电池容量的增加，电动汽车配送成本总体降低;随着电费的下降,配送成本出现了一定范围的波动,说明充电时间和电池容量对配送成本有较大影响,而电费对配送成本的影响相对较小;当这3个因素变化时,行驶里程和碳排放量均出现波动，并且二者的变化趋势大致相同，说明碳排放量与行驶里程有较大关系，而与充电时间、电费、电池容量等因素没有直接关系。因此，当充电时间减少、电费下降、电池容量增加时，所取得的经济效益要远大于环境效益。企业在追求配送成本最小化时，可以通过路径优化降低配送里程和碳排放量。

这3种因素中对电动汽车配送成本影响最大的是电池容量，随着电池容量的增加，电动汽车的续航里程增加，充电次数减少，直接影响电动汽车的配送路径，行驶里程和时间成本都会降低，碳排放量也会随着里程的降低而降低。当电池容量足够大时，就不再需要充电，EVRP问题就转化成了传统汽油车的VRP问题，没有了因充电产生的时间成本，配送成本就会大幅降低。充电时间的减少降低了配送的时间成本，但因为无法改变电动汽车续航里程受限的问题，不能直接影响配送路径，所以行驶里程出现波动，碳排放量也随之波动。电费的变化只能影响到能源成本的变化，因此它的变化对行驶里程和碳排放量不能产生直接的影响，又因为能源成本在电动汽车的配送成本中所占比例较小，所以电费的变化对电动汽车配送成本的影响较小。因此，电池容量的增加相对于充电效率的增加和电费的降低更能有效地降低电动汽车配送成本。

为保证结论的普遍性，从文献[13]中选取3种不同规模的实例进行测试，测试结果见表5。表5中体现出来的各因素变化的影响与前述结论一致，而且实例规模越大，因素变化的影响也越大。

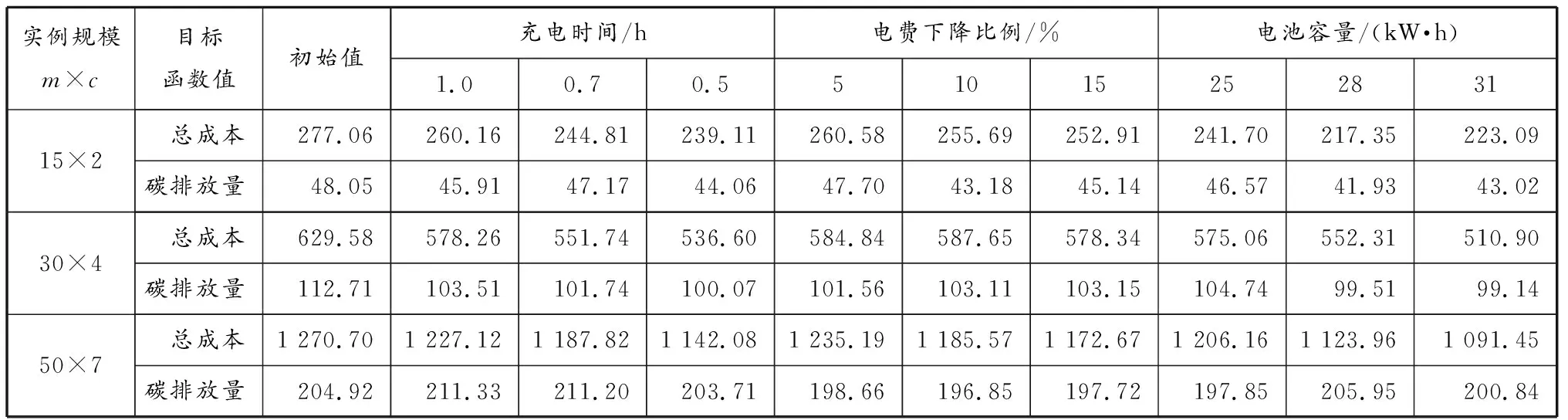
表5 不同规模实例中各因素变化对配送成本和碳排放量的影响

4 结 论

本文研究在社会充电网络已经建设好的情况下，考虑低碳环境下的电动汽车路径问题(EVRP)。从单次配送的角度出发，在考虑车辆能源转化效率的基础上，分别建立综合考虑碳排放和运输费用的传统汽油车VRP模型和EVRP模型，并使用遗传算法对算例进行求解。从两者的优化结果可以看出：在发展低碳物流的过程中，物流企业使用电动汽车虽然会增加配送里程，但能够降低企业的经济负担，明显减少环境污染和能源消耗；对充电时间、电费、配送里程的灵敏度分析发现，充电效率的提高、电池容量的增大可以有效降低企业的经济成本，对碳排放量没有直接影响，但是可以通过路径优化降低配送里程，进而降低碳排放量。未来电池和充电技术的发展会进一步降低电动汽车的配送成本，而环境和能源问题的进一步加剧必然会推动物流企业从使用传统汽油车向使用电动汽车的转型。

本文仅从单次配送的角度出发研究配送成本，没有探究较长时期的成本变化，没有考虑对电动汽车有重要影响的购买成本、维护成本和政府补贴等因素，没有分析车辆生命周期的全部成本。因此，未来的研究内容可以是两种车型整个生命周期内总成本的比较，也可以是同时考虑时速和装载量影响的电动汽车在实际交通网络中的配送模型，以及不确定需求下的电动汽车的配送模型。

参考文献：

[1] 施晓清, 李笑诺, 杨建新. 低碳交通电动汽车碳减排潜力及其影响因素分析[J]. 环境科学, 2013, 34(1): 385-394.

[2] MOLINA J C, EGUIA I, RACERO J,etal. Multi-objective vehicle routing problem with cost and emission functions[J]. Procedia - Social and Behavioral Sciences, 2014, 160: 254-263. DOI: 10.1016/j.sbspro.2014.12.137.

[3] ZHANG Jianghua, ZHAO Yingxue, XUE Weili,etal. Vehicle routing problem with fuel consumption and carbon emission[J]. International Journal of Production Economics, 2015, 170: 234-242. DOI: 10.1016/j.ijpe.2015.09.031.

[4] 钟聪儿, 邱荣祖. 综合考虑碳排放与运输费用的配送路径优化[J]. 数学的实践与认识, 2016, 46(21): 89-94.

[5] 张如云, 刘清. 考虑低碳的城市配送车辆路径优化模型研究[J]. 工业工程与管理, 2015, 20(4): 29-34.

[6] LIN J, ZHOU W, WOLFSON O. Electric vehicle routing problem[J]. Transportation Research Procedia, 2015, 12: 508-521. DOI: 10.1016/j.trpro.2016.02.007.

[8] AFRODITI A, BOILE M, THEOFANIS S,etal. Electric vehicle routing problem with industry constraints: trends and insights for the future research[J]. Transportation Research Procedia, 2014, 3: 452-459. DOI: 10.1016/j.trpro.2014.10.026.

[9] 杨珺, 冯鹏祥, 孙昊, 等. 电动汽车物流配送系统的换电站选址与路径优化问题研究[J]. 中国管理科学, 2015, 23(9): 87-96. DOI: 10.16381/j.cnki.issn1003-207x.2015.09.011.

[10] 揭婉晨, 杨珺, 陆坚毅. 基于分支定价算法的电动汽车车辆路径问题[J]. 运筹与管理, 2016, 25(4): 93-100.

[11] XIAO Yiyong, ZHAO Qiuhong, KAKU I,etal. Development of a fuel consumption optimization model for the capacitated vehicle routing problem[J]. Computers & Operations Resurch, 2013, 39: 1419-1431. DOI: 10.1016/j.cor.2011.08.013.

[13] 占焱发. 基于遗传算法的物流配送车辆路径问题研究[D]. 西安: 长安大学, 2010. DOI: 10.7666/d.Y1729718.

[14] 郁磊, 史峰, 王辉, 等. 智能算法[M]. 2版. 北京: 北京航空航天大学出版社, 2015: 38-49.

[15] RENAULT. Kangoo-brochure[EB/OL]. (2017-01-01)[2017-02-11].http://brochures.renault.co.uk/?moicodes=K62.

[16] AKÇELIK R, BESLEY M. Operating cost, fuel consumption, and emission models in aaSIDRA and aaMOTION[C]//Conference of Australian Institute of Transport Research. Australia: University of South Australia, 2003.

[17] GENTA G. Motor vehicle dynamics: modelling and simulation[M].Singapore: World Scientific Publishing, 1997: 379-421.

[18] GIANNELLI R A, NAM E K, HELMER K,etal. Heavy-duty diesel vehicle fuel consumption modeling based on road load and power train parameters[J]. Center for Environmental Research & Technology, 2005: 1-16. DOI: 10.4271/2005-01-3549.

[19] TESLA WEBSITE. Battery charging and discharging losses[EB/OL].(2011-07-21)[2017-02-11]. https://forums.tesla.com/it_IT/forum/forums/battery-charging-and-discharging-losses.

[20] 中国碳排放交易网. 2014年4月9日国内碳排放交易价格[EB/OL]. (2014-04-09)[2017-02-11]. http://www.tanpaifang.com/tanshichang/201404/0930834.html.

[21] STATISTA. Global average electricity price by key country 2015[EB/OL]. (2015-12-17)[2017-02-11]. https://www.statista.com/statistics/477995/global-prices-of-electricity-by-select-country.

[22] 江苏省环境监测中心. 碳排放量计算[EB/OL]. (2012-06-07)[2017-02-11]. http://www.jshb.gov.cn:8080/pub/shczx/jcxbk/dtcx/201607/t20160711_361527.html.

[23] INTERNATIONAL ENERGY AGENCY IEA. CO2emissions from fuel combustion[EB/OL]. (2016-11-16)[2017-02-11]. http://www.iea.org/media/statistics/CO2Highlights.XLS.