电动汽车充电站分层递进式选址方法研究*

任其亮，吴丽霞，靳旭刚，苏莉晓

(重庆交通大学 交通运输学院，重庆 400074)

0 引 言

截至2015年底，全国机动车保有量达2.79亿辆，机动车石油消耗量高达全国石油总产量的85%。面对大量汽柴油车导致的日益严重环境污染和能源消耗问题，高效、节能、零排放的电动汽车越来越受到关注。然而，电动汽车的推广速度却很缓慢，其主要原因与充电站等电动汽车发展配套基础设施不够完善息息相关。因此，拥有一套科学合理的充电站选址规划方法，对推动城市电动汽车发展、降低环境污染和节约能源均具有重要的现实意义。

目前，国内外众多学者对电动汽车充电站选址的研究，主要是充电站建设原则、影响因素、可行性、选址模型及算法求解的研究。C.E.HATTON等[1]阐述了充电设施对电动汽车普及发展的重要性及充电设施建设模式等，给出了建设各种充电设施需要满足的条件；居勇[2]根据当前电动汽车发展需求及充电站布局影响因素的分析，从多个角度论述充电站建设的效益；鲁莽等[3]详细介绍了国内外充电设施发展情况，对充电设施运营的3种商业模式优缺点进行评价研究；WANG Hengsong、高赐威等[4-5]通过选址影响因素的综合考虑，建立了充电站选址规划模型；李菱等[6]通过对电动汽车总量及分布的预测，建立了充电站的年建设总成本最低模型，并运用遗传算法对其求解；张国亮[7]对不同等级充电站特点的分析，提出了充电站建设成本和用户行驶成本总成本之和最小的数学模型，并利用改进的禁忌搜索算法求解；何战勇[8]建立了充电站运行成本和用户充电成本之和最小的数学模型，并给出了模型求解算法。

现有研究多是充电站选址的理论研究，定量建模选址研究不多，还未形成一套系统、完整的选址方法。笔者先考虑交通、环境、土地、电力等因素，利用熵权模糊物元法对选址影响因素进行量化，确定充电站初选位置，然后在初步选址基础上以充电站总建设成本最小为目标建立数学模型用于精确选址。通过定性、定量分析相结合方法对充电站进行分层递进式选址，形成一套较为系统、完善的充电站选址方法。

1 电动汽车充电站选址条件

充电站选址涉及的因素较为复杂，根据评价指标选取原则和相关因素分析，从交通因素、环境因素、电力因素、规划因素、土地因素以及成本6个方面分析，建立充电站选址评价指标体系，该体系共3层，第1层为目标层，确定充电站的选址评价指标体系；第2层为准则层，包含交通、环境、电力、规划、土地、以及成本因素6个影响选址的主要因素；第3层为次准则层，分别为交通便利性、道路网状况、社会环境影响性、对电网的影响等14个评价指标，运用层次分析法建立评价指标体系如图1。

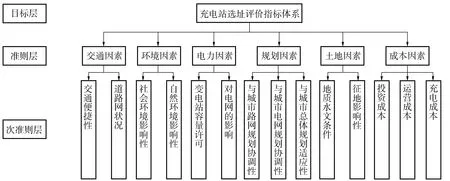
图1 充电站选址评价指标体系Fig. 1 Evaluation index system of Charging station site selection

2 基于熵权模糊物元法的充电站初步选址

传统的充电站选址方法很难确定这些因素的权系数或有较强的主观臆断性，笔者引入熵权模糊物元法进行初步选址，可以有效避免主观因素带来的影响，使权重计算更为科学、合理。具体方法如下：

1) 构造复合模糊物元

若建立的评价指标体系U有u个待评指标C1，C2，…，Cu，及相对应的模糊量值为x1，x2，…，xu，此时称R为u维模糊物元。当Rvu表示v个待评事物的u维复合模糊物元，则xji称为第j个样本的第i项指标的模糊量值(j=1，2，…，v；i=1，2，…，u)。

2) 计算从优隶属度

从优隶属度指各单项评价指标相应的模糊量值与标准样本评价指标对应的模糊量值的接近程度，以此为原则建立从优隶属度关系。

3) 标准模糊物元和差平方模糊物元

建立u维标准模糊物元R0u，由复合模糊物元Rvu中待评价指标从优隶属度中的最大、最小值确定R0u值，Δji(j=1，2，…，v；i=1，2，…，u)为标准模糊物元R0u和复合模糊物元Rvu中各元素的差的平方，由此得到差平方复合模糊物元RΔ。

4) 确定熵权

由各评价指标值组成的判断矩阵决定各指标权重，提高评价结果精确性。其计算步骤如下：

① 建立v个事物u个评价指标的判断矩阵：

R=(xji)vu， (j=1，2，…，v；i=1，2，…，u)

(1)

② 将判断矩阵归一化处理，得矩阵B，矩阵B的元素为：

对于越小越优型指标为

(2)

对于越大越优型指标为

(3)

式(2)、式(3)中，在相同的评价指标体系下，minxji表示最不满意，maxxji表示最为满意。

③ 定义熵。在v个评价事物u个评价指标中，第i个评价指标的熵Hi为

(4)

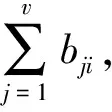
(5)

④ 计算评价指标熵权Wi为

(6)

⑤ 欧式贴近度计算。通过贴近度值对备选点进行筛选，确定候选站点。笔者采用(*，+)算法，即先乘再加法构造欧式贴近度的复合模糊物元RPH：

(7)

式中：

(8)

3 充电站精确选址模型

3.1 模型假设

在建立模型时做如下假设：

1) 充电站的选址点都考虑了需求分布，并符合充电站建设的环境和安全条件；

2) 每个需求点处的需求量表示该区域内电动汽车充电需求数量；

3) 电动汽车剩余电量足够到达充电站；

4) 充电用户熟悉充电站位置，均去最近点充电；

5) 充电用户充电费用与行驶距离为线性关系，且行驶距离为欧氏距离。

3.2 目标函数

笔者建立的精确选址模型主要从充电站建设方与充电用户方两个方面考虑[9-10]。以充电站总建设总成本最小为目标，具体模型为

minf=f1+f2

(9)

式中：f1为充电站建设成本函数，包括不同等级充电站建设初期固定投资成本，充电站的运行成本(充电站日常的维系保养费、材料费等)；f2为用户充电成本函数，主要是电动汽车用户去充电站路上的行驶成本。

(10)

(11)

式中：i为需求点；j为候选点；Em为m等级充电站建设初期固定投资费用；r为贴现率；t为资金回收期；α为充电站运行成本与初期固定投资成本的折算系数；λ为用户充电电价；k为道路侧曲折系数；Di为需求点i处的需求量；dij需求点i到候选点j的距离。

将式(10)、式(11)代入到式(9)中，可得：

(12)

3.3 约束条件

(13)

Zij≤Xjm∀i∈I，j∈J，m∈M

(14)

(15)

(16)

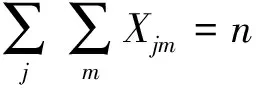
(17)

dij≤dmax

(18)

Xjm=0，1 ∀j∈J，m∈M

(19)

Zij=0，1 ∀i∈I，∀j∈J

(20)

式中：I为所有充电需求点的集合；J为所有候选点的集合；约束(13)表示一个需求点只到一个充电站充电；约束(14)表示只有在候选点建设充电站才能提供充电服务；约束(15)表示充电需求必须在充电站服务能力范围内，其中Cm为m等级的充电站日服务车辆数；约束(16)表示每个候选点处只建立一种等级充电站；约束(17)表示候选点中选择n个建立充电站；约束(18)表示用户的充电距离不能大于充电站的服务半径；约束(19)、(20)为两个0-1决策变量，Xjm={0，1}，在候选点j处建立m级充电站等于1，否则为0；Zij={0，1}，在候选点j接受服务等于1，否则为0。

3.4 遗传算法求解模型

笔者建立的充电站精确选址模型参变量多，约束条件也较为复杂，使用传统算法难以在较短时间内得到模型最优解，因此笔者运用遗传算法对模型进行优化求解。

1) 确定适应度函数

适应度函数由选址模型中求最小值的目标函数决定的，本文目标函数f(x)到个体适应度函数F(x)的转换方法如式(21)，其中Amax为当前f(x)的最大值。

(21)

2) 遗传算法求解过程

Step0：随机产生初始种群；

Step1：将初始种群带入适应度函数(21)中计算，得到每个个体适应度值，按照从大到小顺序排序；

Step2：从初始种群中按照0.3概率选择较优解复制到下一代中；剩余的初始种群再运用轮盘赌法选择操作；

Step3：按照相应的交叉，变异概率产生新的个体；

Step4：当交叉变异产生新的种群后，再转入Step1；

Step5：当交叉变异达到最大迭代次数时，算法终止。

4 算例分析

4.1 算例描述

从40×40平面内随机产生20个充电需求点和8个备选站点，假设每个充电需求点的需求量在(25，45)内，即每个充电需求点处有25～45辆车有充电需求。充电需求点及备选充电站的平面位置分布如图2，需求点的位置、需求量及备选站点分布如表1、表2，假设共有4种等级的充电站，对每种等级充电站服务能力及建设成本进行合理假设，如表3。

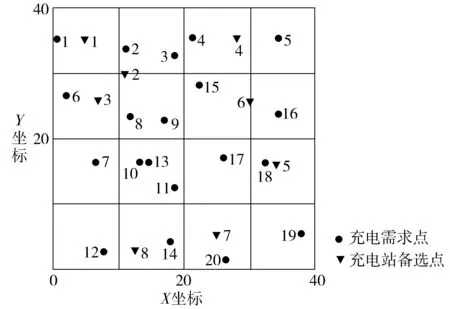
图2 充电站需求点及备选点分布Fig. 2 Distribution map of demand and alternative point about charging station locations

4.2 初步选址

根据电动汽车充电需求及分布，现已确定了8座备选充电站，首先初选5座充电站。再根据相关政策及充电站服务能力等确定最终充电站建设数量。采用专家咨询法筛选指标，最终建立了6个事物，14个评价指标的复合模糊物元。8座备选充电站的基本情况如表4。

表1 充电站需求点位置及需求量Table 1 Location and demand of charging station demand point

表2 备选站点位置Table 2 Alternative site location

表3 不同等级充电站建设成本Table 3 Construction cost of charging stations with different grades

表4 备选充电站的基本情况Table 4 Basic situation of alternative charging station

根据表4建立评价指标，构建复合模糊物元，通过计算得8座备选充电站的欧式贴近度RPH值：

根据欧式贴近度RPH结果可得各备选充电站的排序为：2>4>6>8>7>3>1>5，因此，初选后的5座候选站分别为：2、4、6、7、8号。初选后候选点和充电需求点位置如图3。

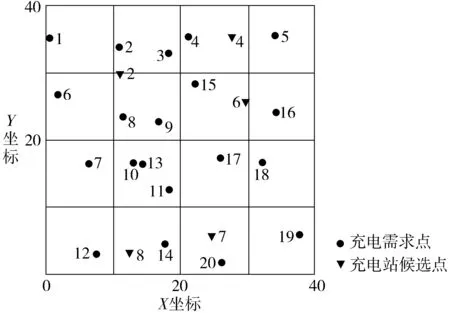
图3 初步选址后分布Fig. 3 Distribution map after preliminary site

4.3 精确选址

根据充电站建设相关政策、用户充电需求分布及充电站建站数目对成本和服务能力的影响分析，最终选择3个候选点进行充电站建设，以总建设成本最小为目标建立精确选址模型，利用遗传算法求解模型，具体参数取值如表5。

表5 参数取值Table 5 Parameter selection

根据上述算法，利用MATLAB进行编程，参数设置为：种群大小为50、交叉概率为0.6、变异概率为0.008、最大迭代次数为150，A取较大值，使F(x)均为正值，本文A取40 000，对该假设算例独立运行30次，充电站最终选址和服务区域划分平面示意如图4。

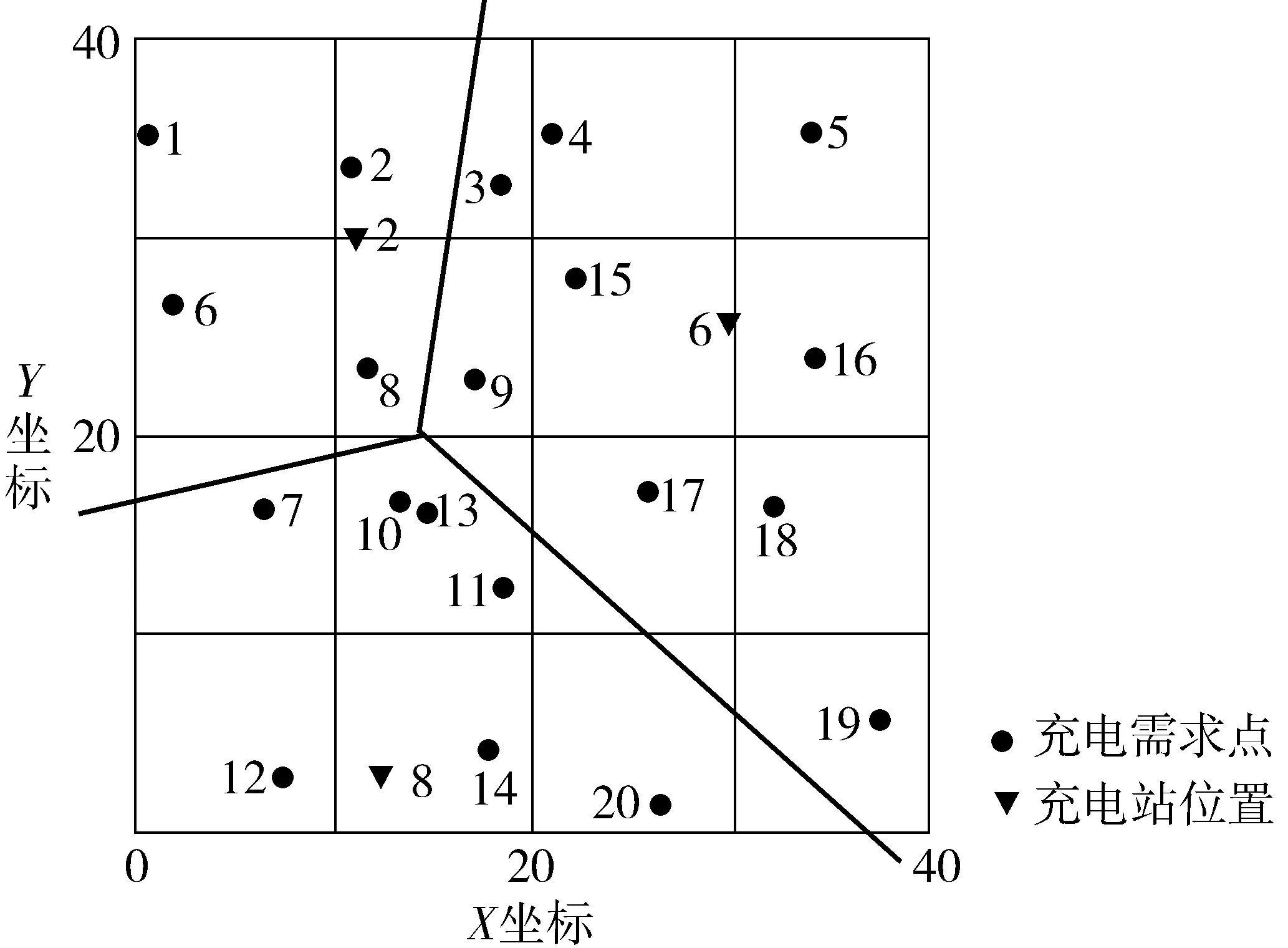
图4 充电站位置及服务区域划分Fig. 4 Construction location of charging station and its service area division

由图4可以看出，最终选择2、6和8号作为充电站建设点，其中各站点的建设等级、建设总成本和服务需求点如表6。

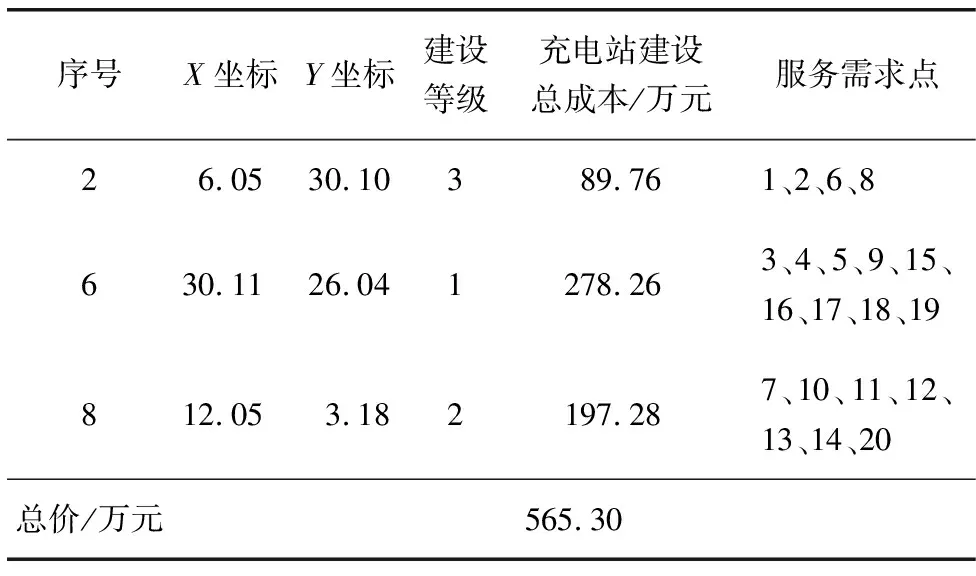
表6 充电站选址结果Table 6 Results of charging stations site selection

5 结 论

笔者采用分层递进式方法进行充电站选址，首先运用熵权模糊物元法初步选址，然后在初步选址的基础上建立数学模型精确选址。确定充电站建设最优位置及建设等级。研究成果主要有以下几点：

1) 充分考虑影响电动汽车充电站选址的交通、环境、电力、规划等因素，构建充电站选址指标体系，运用熵权模糊物元法初步选址，可以有效避免因指标权重主观臆断带来的影响，且量化了选址结果，使初选结果更加清晰。

2) 确定充电站候选站址后，建立基于充电站建设方和充电用户总成本最小的精确选址模型，利用遗传算法进行最终建设方案的求解，验证了该方法的可行性、合理性。

参考文献(References)：

[1] HATTON C E，BEELLA S K，BREZET J C，et al.Charging stations for Urban Settings the design of a product platform for electric vehicle infrastructure in Dutch cities[J].WorldElectricVehicleJournal，2009，1(1)：0134-0146.

[2] 居勇.建设电动汽车充电站的约束条件及综合效益分析[J].华东电力，2011，39(4)：547-550.

JU Yong.Electric vehicle charging station constraint conditions and comprehensive benefit analysis[J].EastChinaElectricPower，2011，39(4)：547-550.

[3] 鲁莽，周小兵，张维.国内外电动汽车充电设施发展状况研究[J].华中电力，2010，23(5)：16-30.

LU Mang，ZHOU Xiaobin，ZHANG Wei.Research on development of charging facilities for electric[J].CentralChinaElectricPower，2010，23(5)：16-30.

[4] WANG H，HUANG Q，ZHANG C，et al.A novel approach for the layout of electric vehicle charging station[C]//InternationalConferenceonApperceivingComputingandIntelligenceAnalysis.[S.l.] ：IEEE，2010：64-70.

[5] 高赐威，张亮，薛飞，等.考虑集中型充电站定址分容的电网规划研究[J].中国电机工程学报，2012，32(7)：40-46.

GAO Ciwei，ZHANG Liang，XUE Fei，et al.Grid planning considering capacity and site of large-scale centralized charging stations[J].ProceedingsoftheCSEE，2012，32(7)：40-46.

[6] 李菱，李燕青，姚玉海，等.基于遗传算法的电动汽车充电站的布局规划[J].华东电力，2011，39(6)：1004-1006.

LI Ling，LI Yanqing，YAO Yuhai，et al.Layout planning of electric vehicle charging stations based on genetic algorithm[J].EastChinaElectricPower，2011，39(6)：1004-1006.

[7] 张国亮.城市内和城市间电动汽车充电站的选址布局研究[D].天津：天津大学，2012.

ZHANG Guoliang.ResearchontheLocationProblemofElectricVehicleChargingStationIntra-CityandInter-City[D].Tianjin：Tianjin University，2012.

[8] 何战勇.电动汽车充电站规划方法及运营模型研究[D].北京：北京交通大学，2012.

HE Zhanyong.ResearchonPlanningMethodandOperationModeofElectricVehicleChargingStation[D].Beijing：Beijing Jiaotong University，2012.

[9] 宋志成，王勋，伦利，等.基于收益最大化的电动汽车充电站选址规划[J].华东交通大学学报，2014，31(1)：50-55.

SONG Zhicheng，WANG Xun，LUN Li，et al.Planning of site selection of electric vehicle charging stations based on the maximum profits[J].JournalofEastChinaJiaotongUniversity， 2014，31(1)：50-55.

[10] 张国亮，李波，王运发.多等级电动汽车充电站的选址与算法[J].山东大学学报(工学版)，2011，41(6)：136-142.

ZHANG Guoliang，LI Bo，WANG Yunfa.Location and algorithm of multi-level electric vehicle charging stations[J].JournalofShandongUniversity(EngineeringScience)，2011，41(6)：136-142.