EPS系统在路面激励下的汽车操纵稳定性响应研究*

李志鹏，史松卓

(东北林业大学 交通学院，黑龙江 哈尔滨 150040)

0 引 言

电动助力转向系统(electric-power-steering system简称EPS)与传统液压助力转向系统相比具有节能环保、助力大小便于调整和能够提供更加准确的“路感”信息的优点，已成为汽车必备零部件。电动助力转向系统的助力转矩由电动机提供，助力转矩数值与电机电流成正比例关系。对电机目标电流良好的跟随特性是EPS系统稳定工作的保证。车辆处于转向工况时会遇到路面随机冲击影响使车辆产生振动，影响车辆的操作稳定性和转向平顺性。因此，研究路面随机冲击对车辆转向操作稳定性和平顺性的影响尤为重要。

转向系统的振动主要分为由系统自身阻尼作用和黏滞作用产生的共振、由路面冲击产生的振动和在怠速工况下由发动机产生的振动，文献[1]通过软件建模计算出EPS系统振动的固有频率，通过优化整车参数，避免发动机在怠速工况下与EPS转向系统产生共振；文献[2]设计了一种电流补偿算法，以折算到小齿轮上的路面冲击力为依据计算电机补偿电流，以减轻路面冲击对电动助力转向系统性能的影响；文献[3]针对车辆转向时轮胎产生振动的现象，提出了一种抑制轮胎振动的控制算法，该算法通过估算电机的振动频率，通过阻尼作用控制电机角速度，达到降低轮胎振动对转向性能产生不良影响的目的。

笔者的研究重点为在整车动力学模型的基础上将路面随机激励作为车辆振动的主要振动源，通过仿真比较整车动力学模型中表征车辆运动特性的参数值，将基于趋近率的滑膜控制算法应用于EPS系统并分析该控制算法对于车辆操纵稳定性的影响。

1 整车12自由度模型[4-5]

牛顿经典运动学理论分别列出车辆在纵向、侧向、垂向、侧倾、横摆、俯仰6个自由度的动力学方程、车辆垂向动力学方程以及转向盘转角与车轮转角的换算方程。

1) 车辆纵向运动方程

(FxFL+FxFR)cosδ-(FyFL+FyFR)sinδ-FxRL-FxRR

(1)

式中：m为整车质量，kg；ms为悬挂质量，kg；Fxi为车轮纵向力，N；Fyi为车轮侧向力，N；δ为车轮转角,(°)。

2) 车辆侧向运动方程

FxFR)sinδ+(FyFL+FyFR)cosδ+FxRL+FxRR

(2)

3) 车辆垂向运动方程

ksFL(zsFL-zuFL)-ksFR(zsFR-zuFR)-ksRL(zsRL-zuRL)-

(3)

式中：ksi为悬架弹簧刚度,(N·m-1)；csi为悬架减震器阻尼系数,(N·m·s·rad-1)；zsi为悬挂质量位移，m；zui为非悬挂质量位移，m。

4) 车辆横摆运动方程

dF[(FxFL-FxFR)cosδ+(FyFL-FyFR)sinδ] +dR(FxRL-

FxRR)+lF[(FxFL+FxFR)sinδ+(FxFL+FxFR)cosδ] -

lR(FxRL+FxRR)

(4)

式中：Iz为整车绕z轴的转动惯量，(kg·m2)；Ixs为整车绕x轴的转动惯量，(kg·m2)。

5) 车辆侧倾运动方程

ksFR(zsFR-zuFR)dF-ksRL(zsRL-zuRL)dR+ksRR(zsRR-

(5)

式中：Ixu为悬挂质量绕x轴的转动惯量,(kg·m2)；Ixzu为悬挂质量绕x、z轴的惯性积,(kg·m2)；Iys为悬挂质量绕y轴的转动惯量,(kg·m2)；Izs为悬挂绕z轴的转动惯量,(kg·m2)。

6) 车辆俯仰运动方程

zuFL)cF+ksFR(zsFR-zuFR)cF-ksRL(zsRL-zuRL)cR+

(6)

路面随机激励产生的垂向位移会影响车辆的垂向受力，引入车辆垂向动力学方程；车辆垂向运动方程分别为

(7)

(8)

(9)

(10)

驾驶员通过施加力到转向盘上，使转向盘产生相应的转角，通过转向系统将转向盘的转角转换为车轮的转角，实现车辆的转向。由于转向传动机构和轮胎回正力矩的存在转向盘转角与前轮转角存在相应的换算关系，式(11)给出了转向盘转角与前轮转角的换算关系式。

转向盘转角与前轮转角关系式：

(11)

式(1)～式(11)中的变量分别为：δ为前轮转向角，(°)；mt1、mt2、mt3、mt4为非悬挂质量,kg;ks1、ks2、ks3、ks4为悬架刚度系数;v为车辆水平方向速度,(m·s-1)；kt1、kt2、kt3、kt4为轮胎刚度;xr1、xr2、xr3、xr4为路面激励输入，m;xt1、xt2、xt3、xt4为非簧载质量位移;xs1、xs2、xs3、xs4为悬挂质量与悬架连接处的位移，m;n为转向系总传动比；ms为悬架质量,kg;k为转向系刚度；Ml1、Ml2为车辆左、右前轮回正力矩，(N·m)；cs1、cs2、cs3、cs4为左前、左后、右前、右后车轮等效阻尼系数，(N·m·s·rad-1)。

2 EPS系统动力学模型

笔者以转向柱式电动助力转向系统为例，系统由ECU控制器、助力电机、涡轮蜗杆减速机构、转向管柱、扭矩传感器和齿轮齿条转向机构组成，如图1。

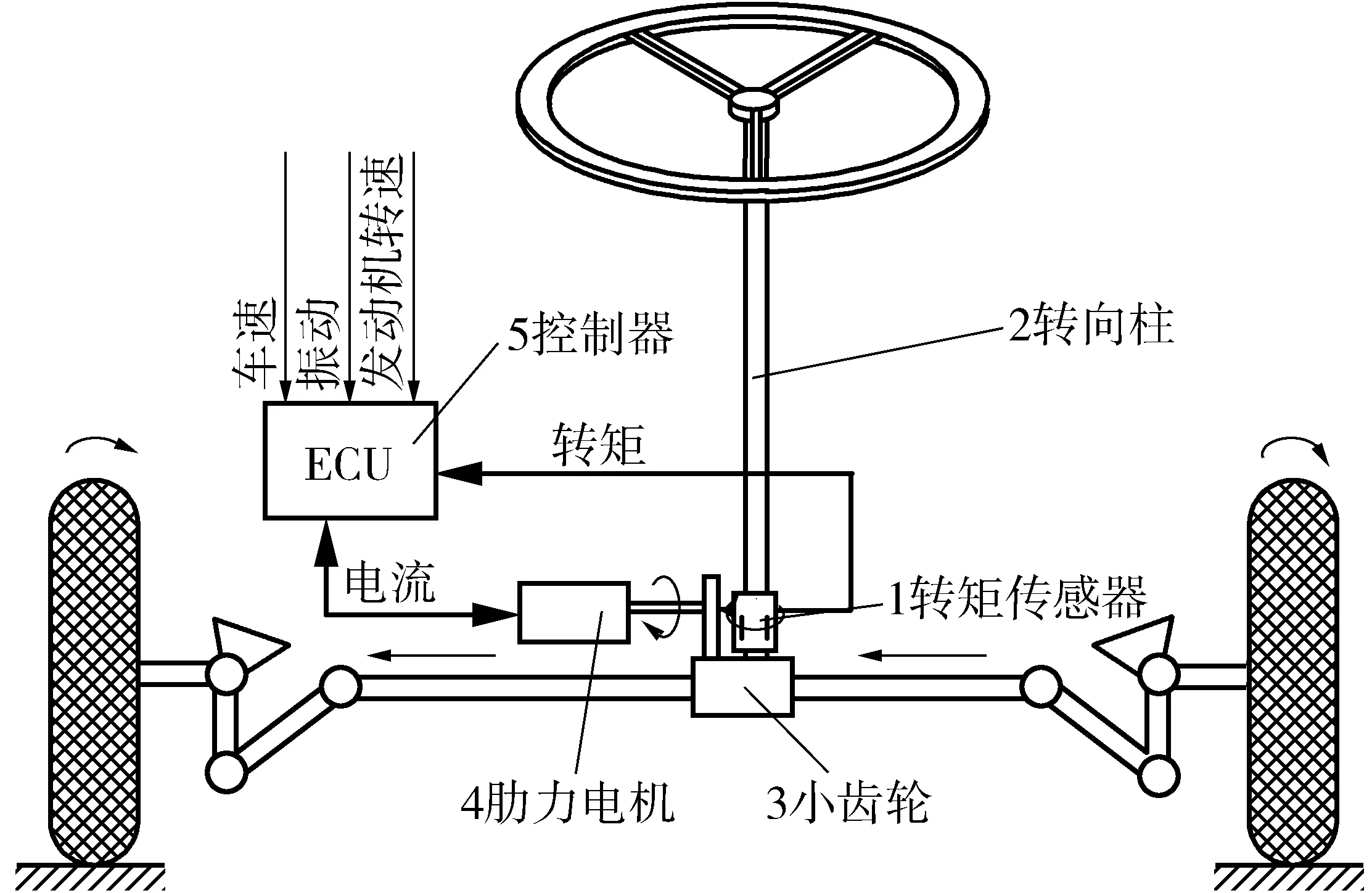
图1 电动助力转向系统组成框图Fig. 1 Diagram of electric power steering system

转向系统动力学方程[7]。

转向柱：

(12)

扭矩传感器值：

Ts=ks(θs-θe)

输出轴：

(13)

齿条：

(14)

电动机机械特性：

(15)

电机数学模型：

(16)

电机助力力矩：

Ta=kmG(θm-Gθe)

(17)

(18)

D=[0]

式中：Jm为电机转动惯量,(kg·m2)；Bs为转向柱阻尼系数,(N·m·s·rad-1)；Be为减速机构阻尼系数,(N·m·s·rad-1)；Bm为电机阻尼系数,(N·m·s·rad-1)；θs为管柱输入轴转角,(°)；θe为管柱输入轴转角,(°)；Ts为扭矩传感器检测值,(N·m)；ks为扭矩传感器刚度系数；km为电机转矩系数；Tm为电机电磁转矩,(N·m)；Ta为电机助力转矩,(N·m)；Td为转向盘输入转矩,(N·m)；xr为齿条位移,m；r为小齿轮半径,m；im为电机电流,A；mr为小齿轮与齿条总质量,kg；br为齿条长黏滞系数；L为电机等效电感,H；R为电机等效电阻,Ω；Kf为电机反电动势系数；G为减速机构传动比；U为电机电压,V；Tw为轮胎于路面作用力,(N·m)；Js为转向柱转动惯量,(kg·m2)；Je为减速机构转动惯量,(kg·m2)。

不考虑轮胎与转向系统之间的力传递特性，将轮胎的回正力矩传递到转向输出轴上。

3 轮胎模型

转向盘转角与前轮转角换算关系中需要用到轮胎的回正力矩，有必要引入轮胎力学模型。由于轮胎的受力受多方面因素如轮胎材质、胎压以及轮胎的定位参数等因素的影响，建立相对完善的轮胎模型较为复杂，同时考虑到转向系统机械特性和轮胎定位参数的影响笔者引用摆振系统中的轮胎力学模型[8]，本轮胎模型的建立是根据轮胎经验和半经验模型，假设轮胎在小形变的情况下是线性系统的前提下建立的。

(19)

(20)

式中：Fy为前轮侧向力,N；Kc为轮胎侧向刚度；α为主销后倾角,(°)；R为轮径,m；θ为前轮转角,(°)；Y为悬架与地面距离,m；h为轮心与地面距离,m；φx为前桥绕X轴摆角,(°)；V为车速,(m·s-1)；Ks为轮胎外倾刚度；KP为轮胎侧偏刚度；A为车轮前束角，(°)；Kε为轮胎外倾刚度；ε0为车辆外倾角，(°)。

4 路面不平度时域模型

假设路面随机激励产生的垂向位移无损失的通过轮胎传递到车辆的减震-阻尼系统，基于白噪声建立路面随机激励输入模型如式(21)[6]。

(21)

式中：qi(t)为第i车轮受到的路面不平度随机激励；V为车速，(m·s-1)；α为与路面等级相关的常数；w(t)为白噪声随机信号。

5 基于趋近率的滑模变结构控制器设计

基于趋近率的滑模控制[9]可使系统状态在有限时间内收敛为0，突破了普通滑模控制在线性滑模面条件下状态渐进收敛的特点，系统的动态性能优于普通滑模控制，相对于传统线性滑模控制，可有效的消除抖振。

5.1 滑模控制律的设计

滑模面函数为s=cx，式(22)为系统电流误差：

x=im-i

(22)

将式(16)带入式(22)得趋近率表达式(23)：

(23)

整理得控制器输入量U表达式如式(24)：

(24)

5.2 控制系统稳定性证明

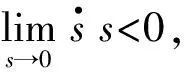
6 仿真计算与结果分析

通过实际测量得到实车仿真参数和EPS系统仿真参数，分别如表1和表2。

表1 某车实测部分仿真参数Table 1 Simulation parameters of car

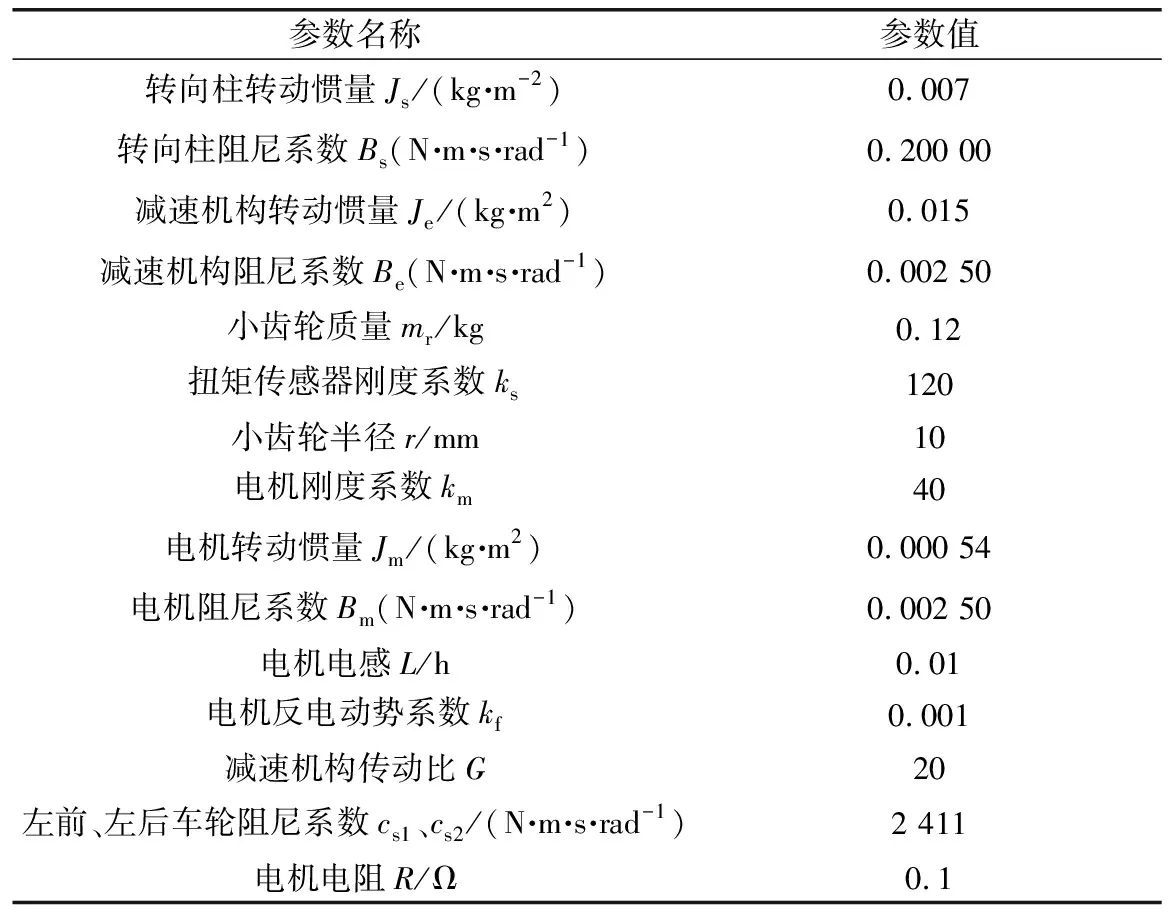
表2 EPS系统参数Table 2 EPS system parameters

以左前轮为例，路面输入激励源为白噪声，路面等级为B级，图2为车轮在路面随机激励下的响应曲线。

图2 轮胎路面激励响应Fig. 2 Tire pavement excitation response

图3和图4为增加滑膜控制器前后系统对电机目标电流跟踪的响应曲线。系统目标电流峰值为±16 A。从图中可以看出增加滑膜控制器后系统对电机目标电流的跟踪响应精度显著提高抖动明显消除，说明滤波器可以有效滤除路面随机激励对控制系统的影响，提高系统的控制精度。

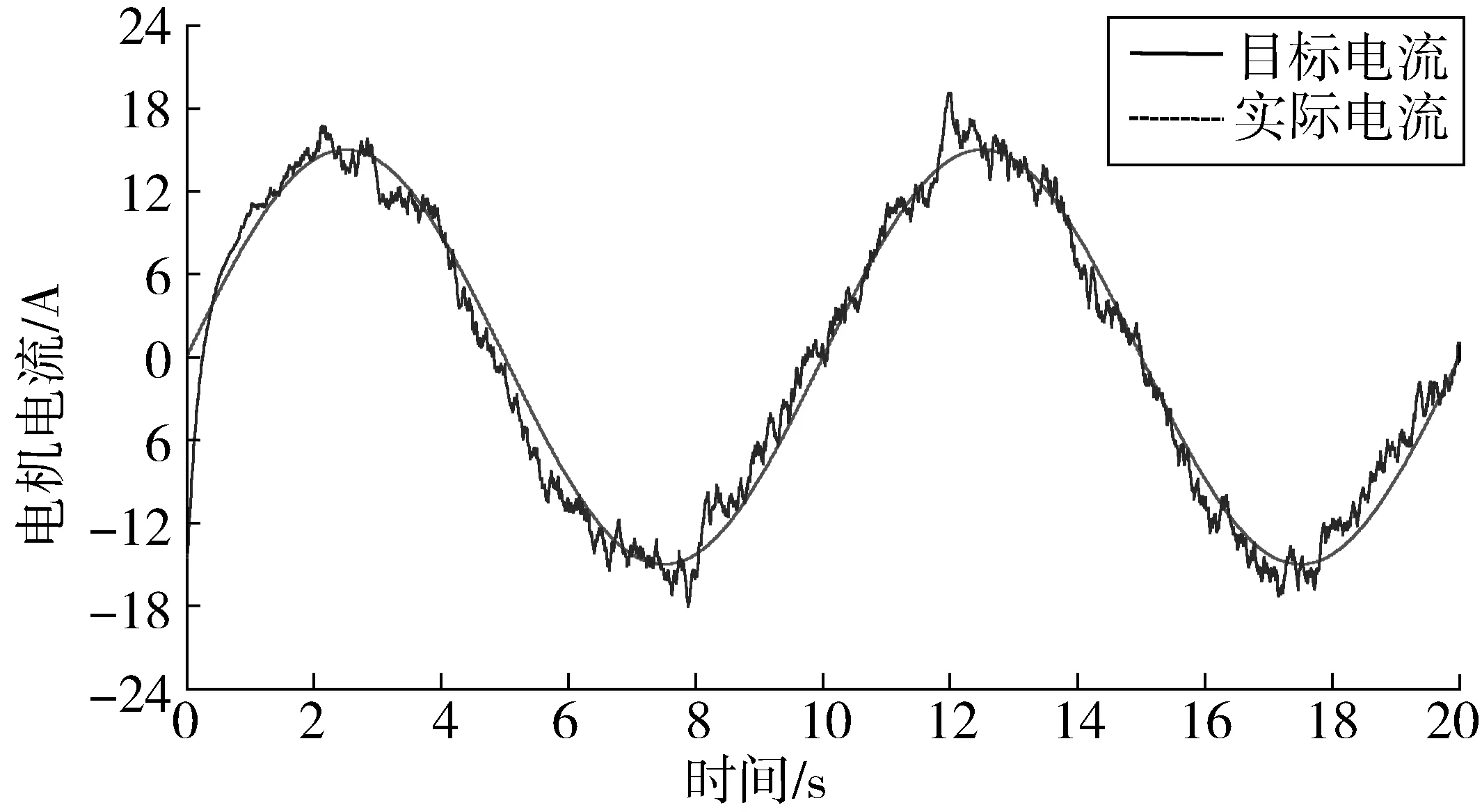
图3 加滑模控制前电流跟踪曲线Fig. 3 Without Sliding mode control current tracking curve

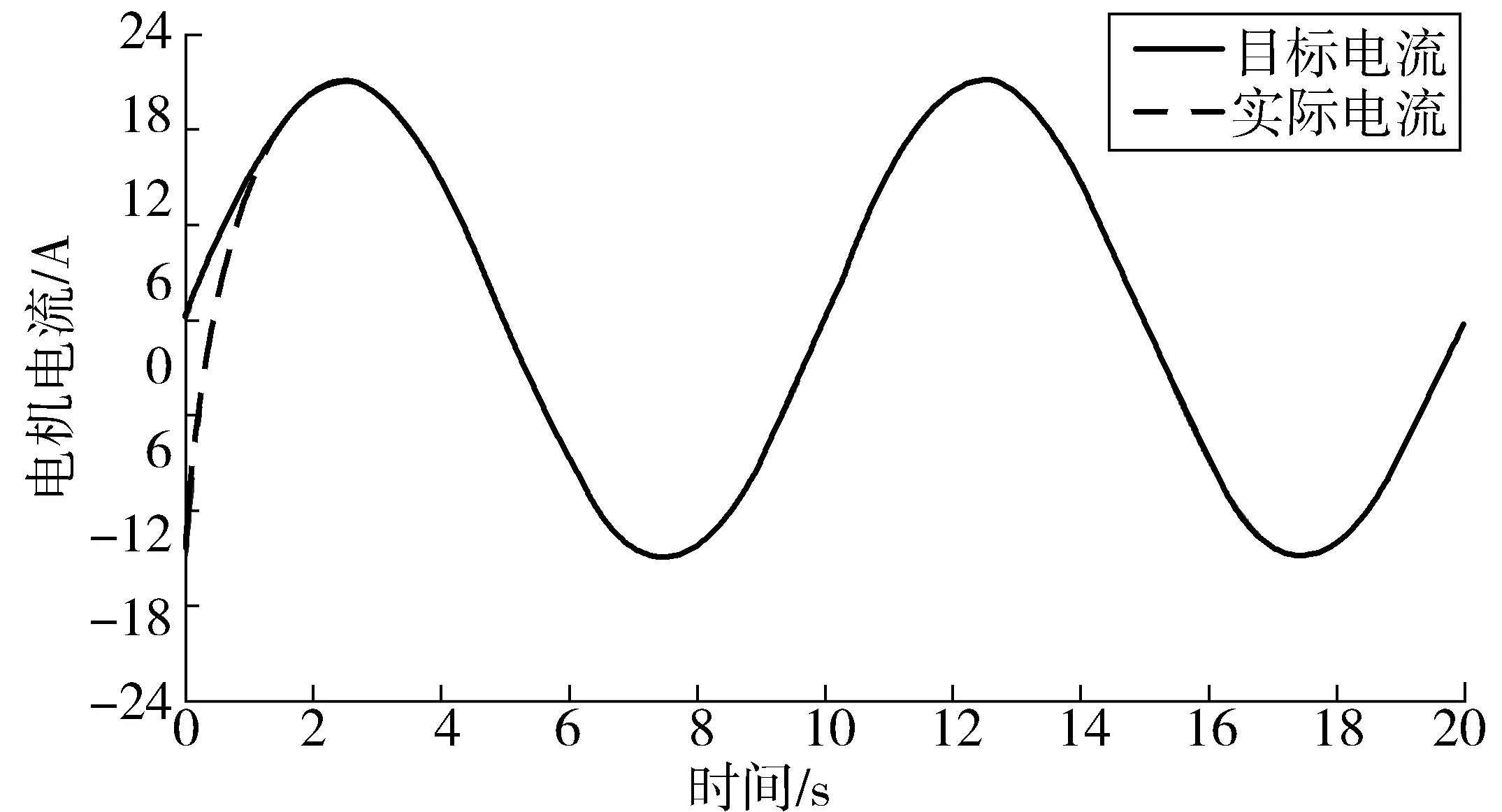
图4 加滑模控制后电流跟踪曲线Fig. 4 With sliding mode control current tracking curve

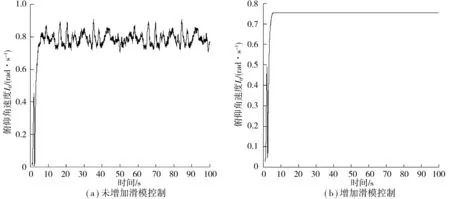
图5 车辆俯仰角速度响应(V=50 km/h)Fig. 5 Vehicle pitch angular velocity response (V=50 km/h)

图6 车辆俯仰角速度响应(V=10 km/h)Fig. 6 Vehicle pitch angular velocity response (V=10 km/h)

由图5和图6可知，随着车速的提高车辆的俯仰角速度逐渐减小，同时增加滑模控制器后在一定程度上减弱了路面冲击对车辆俯仰角速度的影响，车辆的俯仰角速度最终为0.37°；由图7和图8可知，随着车速的提高车辆的侧倾角速度逐渐增大，增加滑模控制器后在一定程度上减弱了路面冲击对车辆侧倾角速度的影响，侧倾角速度最终保持为恒定值，增强了车辆的操纵稳定性。

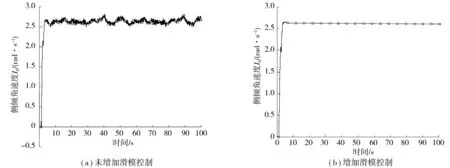
图7 车辆侧倾角速度响应(V=50 km/h)Fig. 7 Vehicle side slope velocity response (V=50 km/h)

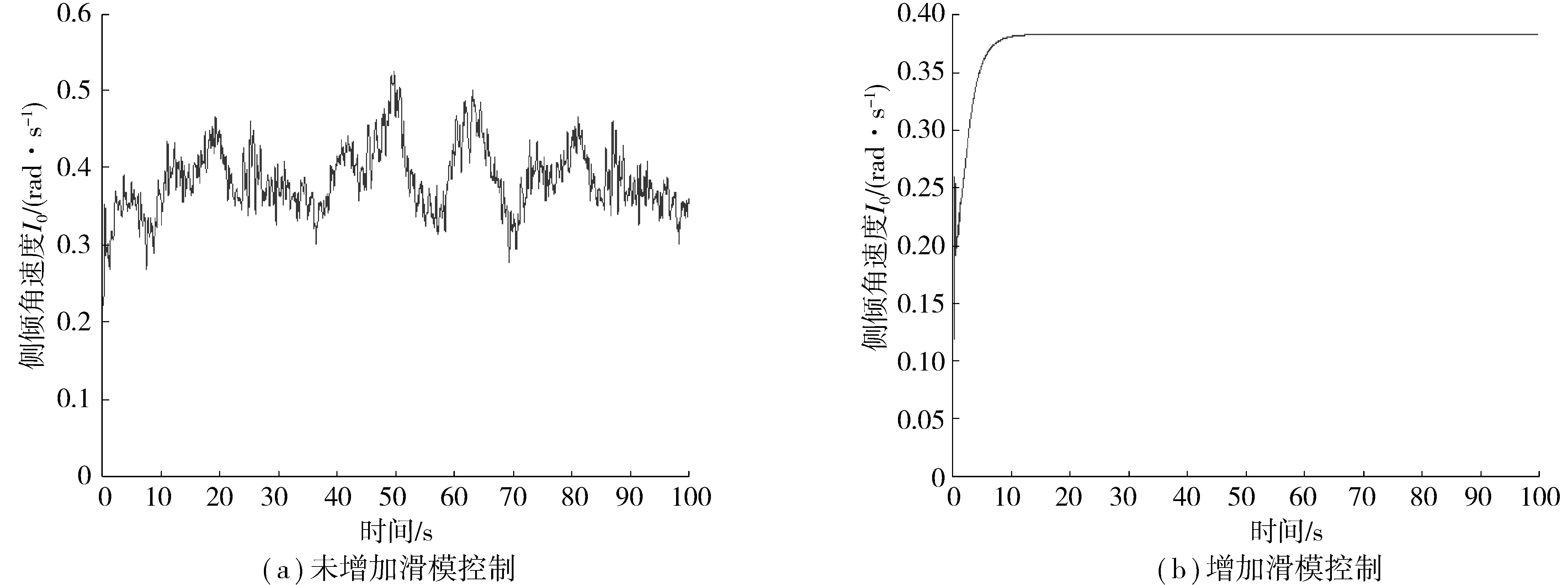
图8 车辆侧倾角速度响应(V=10 km/h)Fig. 8 Vehicle side slope velocity response (V=10 km/h)

图9所示为V=50 km/h、转向盘输入转角为±10°，从图中可知增加滑模控制器后减小了路面激励对转向盘的转矩产生不良影响，基本消除了转向盘在转动过程中产生抖动，增加了转向过程的平顺性。

图9 转向盘转角与转矩响应曲线Fig. 9 Steering wheel angle and torque response curve

7 结 论

1) 建立了包含EPS系统在内的12自由度整车模型。以整车模型为平台研究EPS系统，能够更加真实、可靠的反应当车辆处于转向工况时车辆的俯仰角速度和侧倾角速度，为改善车辆转向系统的操纵稳定性提供理论依据。

2) 在整车模型中引入路面激励模型，将路面的不确定干扰与EPS系统紧密联系起来，为进一步研究路面不平度对EPS系统的影响奠定基础。

3) 基于趋近率的滑膜控制器能够使EPS系统的助力电机快速响应不同的转向工况，在有路面激励输入的情况下，有效减弱路面激励对车辆操纵稳定性产生的冲击，对提高车辆转向的稳定性具有重要的工程实践意义。

参考文献(References)：

[1] 周磊磊.汽车电动助力转向系统振动特性分析[D].合肥：合肥工业大学，2012.

ZHOU Leilei.VibrationCharacteristicsAnalysisonElectricPowerSteeringSystem[D]. Hefei：Hefei University of Technology，2012.

[2] 李绍松，宗长富，何磊.衰减转向盘冲击力矩的电动助力转向控制[J].吉林大学学报(工学版)，2013，43(4)：849-853.

LI Shaosong，ZONG Changfu，HE lei.Control method for electric power steering to reduce impact torque on steering wheel[J].JournalofJilinUniversity(EngineeringandTechnologyEdition)，2013，43(4)：849-853.

[3] SUGIYAMA A，KURISHIGE M，HAMADA H，et al.An EPS control strategy to reduce steering vibration associated with disturbance from road wheels[C]//Sae World Congress & Exhibition，2006.

[4] CROLLA D，喻凡.车辆动力学及其控制[M].北京：人民交通出版社，2004.

CROLLA D，YU Fan.VehicleDynamicsandControl[M].Beijing：China Communications Press，2004.

[5] 崔胜民，肖利寿.汽车操纵动力学十八自由度模型仿真研究[J].汽车工程，1998，20(4)：212-219.

CUI Shengmin，XIAO Lishou.A research on computer simulation for vehicle handling dynamics with 18 DOFs[J].AutomotiveEngineering，1998，20(4)：212-219.

[6] 方浩，李晓宾，王璐.基于路面随机激励的8自由度整车动力学仿真[J].中国工程机械学报，2007，5(2)：168-173.

FANG Hao，LI Xiaobin，WANG Lu.Dynamical simulation of 8-DOF vehicle suspension based on stochastic road surface excitation[J].ChineseJournalofConstructionMachinery，2007，5(2)：168-173.

[7] 王其东，杨孝剑，陈无畏.电动助力转向系统的建模及控制[J].农业机械学报，2004，35(5)：1-4.

WANG Qidong YANG Xiaojian CHEN Wuwei.Modeling and Simulation of Electric Power Steering System[J].TransactionsoftheChineseSocietyforAgriculturalMachinery， 2004，35(5)：1-4.

[8] 陈旻.汽车前轮摆振的研究[D].南京：南京林业大学，2000.

CHEN Min.TheStudyoftheVehiclefrontWheelShimmy[D].Nanjing：Nanjing Forestry University，2000.

[9] 刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2000.

LIU Jinkun.MATLABSimulationforSolidingModelControl[M].Beijing：Tsinghua University Press，2000.