基于NSGA-Ⅱ算法的逆向可变车道信号配时优化*
2018-07-03谢忠金陈科全
刘 伟,谢忠金,陈科全
(重庆交通大学 交通运输学院,重庆 400074)
0 引 言
城市道路车辆的不断增加导致交通拥堵不断加剧,交叉口作为城市道路网络通行能力的瓶颈,是道路拥挤的常发地点,交叉口的运行情况直接影响着整个道路网络的运行。因此,合理地组织管理交叉口能有效的降低城市拥堵。目前在我国城市道路交叉口中,大部分是单点信号控制。针对单点信号交叉口优化,一般分为信号配时优化和交叉口设计优化,信号配时优化方面,F. V. WEBSTER[1]最早将延误作为信号配时优化目标,提出交叉口优化模型,在此之后,众多学者对F. V. WEBSTER提出的延误配时方法做出了改进[2-5],现阶段信号配时多采用多目标优化模型[6-8];交叉口设计方面,最初为了保证车辆有序行驶设计的安全岛和导流车道线等,随着道路交通量的增加,尤其是左转车道交通量增加,出现了左转弯待转区和进口道拓宽设计。赵靖等[9]针对左转车流较大提出一种Exit Lanes For Left-turn 设计,商振华[10]提出了逆向可变车道设计。Exit Lanes For Left-turn和逆向可变车道表达的是同一种设计,针对于城市道路左转车流较大的信号交叉口,在出口道闲置的信号相位阶段时,利用出口道部分车道作为进口道左转车道,通过信号灯控制车辆进入逆向可变车道,如图1。逆向可变车道的设计具有时空互补的优点,同一个周期不同的信号相位充分利用出口道,增加左转进口道车道数,而且改造小,但针对于逆向可变车道的信号交叉口信号配时研究较为简单,将结合逆向可变车道的特点,建立以交叉口通行能力和交叉口控制延误作为目标的优化模型,从整体上对设计逆向可变车道的交叉口进行信号配时优化。

图1 逆向可变车道的进口道功能和出口道功能Fig. 1 Entrance function and exit function of reversing variable lane
1 逆向可变车道分析
1.1 逆向可变车道的设置条件
逆向可变车道可以设置在交叉口左转流量大的进口,位于其相邻出口车道上。一个交叉口多个进口道可同时设置逆向可变车道,但需要满足一些苛刻的条件。逆向可变车道设计直观上增加了左转进口道,可以提高通行能力,但会影响右转进入出口道的车辆行驶,且设置需要对车道精细化的控制和驾驶行为的适应。只有当交叉口左转交通量较大、饱和度较高、拥堵严重,且出口车道通行能力富余时,在确保安全设计的条件下,可设置逆向可变车道。商振华[10]提出设置逆向可变车道的饱和度需超过0.8。在4相位交叉口的一个信号周期内,出口道的出口功能只使用了2个相位时间,可利用另外2个相位时间,将出口道的一条或者多条车道作为与该出口道紧挨着进口道的左转车道,即左转入逆向可变车道等候时,可变车道进口道功能启用,出口道功能关闭,出口道对应的相位处于红灯,此时对相序要求是需要进口道左转相位的上一个相位是与之相交直行相位。为了满足右转进入出口道和逆向可变车道功能同时起作用,出口道至少为2车道。所以逆向可变车道设置条件为:
1) 进口道饱和度较高且左转交通量较大,不能采用空间渠化增加车道来缓解左转交通压力。
2) 有左转车道配时的4相位信号交叉口。
3) 与左转相位相交的直行相位在设置逆向可变车道的左转相位之前放行,典型逆向可变车道相位相序如图2。
4) 出口道车道数至少为2。
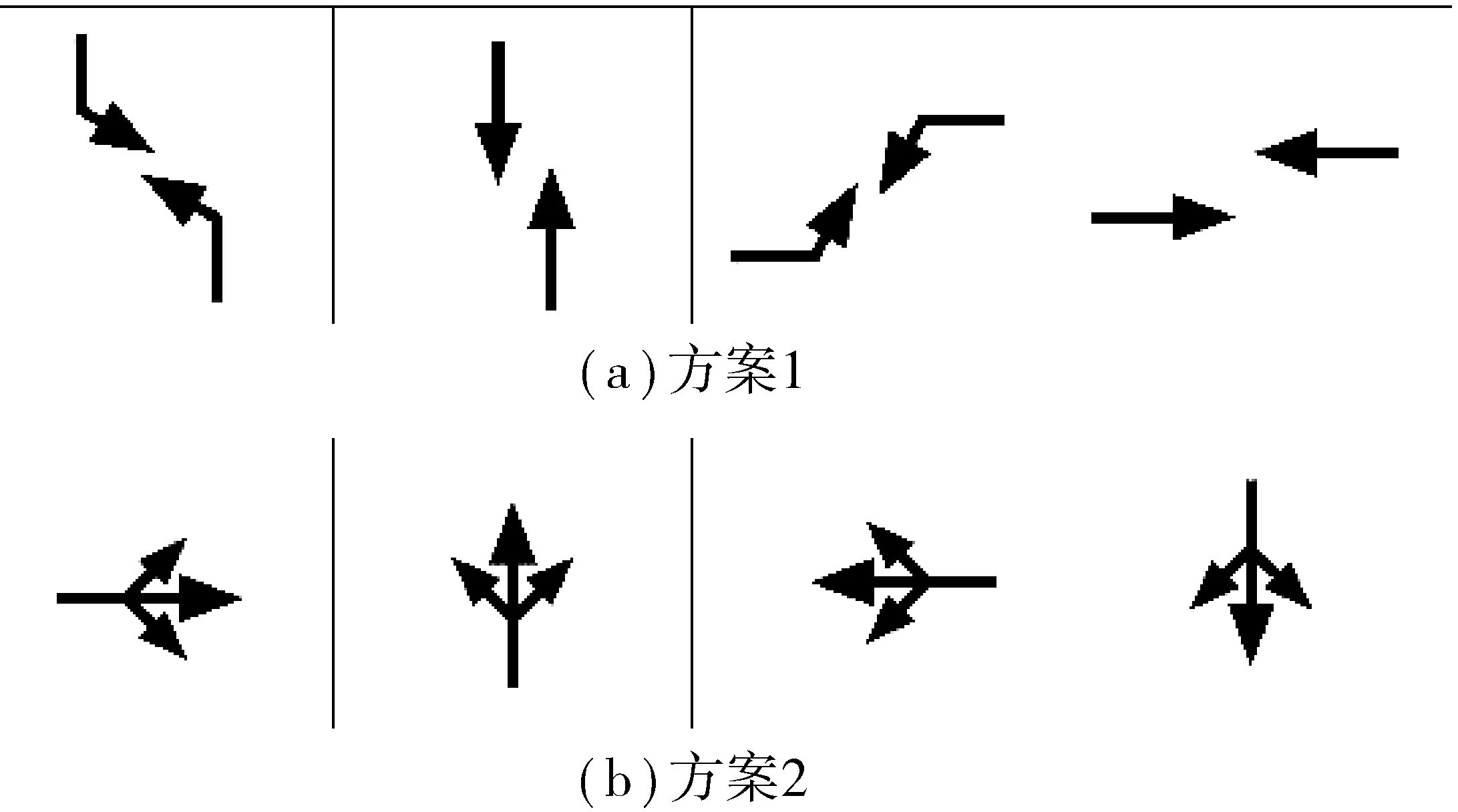
图2 典型逆向可变车道相位相序Fig. 2 Diagram of typical phase and phase sequence of reversing variable lane
1.2 逆向可变车道车辆运行过程分析
1.2.1 进入过程
进入过程需要变逆向可变车道的出口功能为左转进口道功能,即逆向可变车道上出口功能车辆完全清空,除了右转进入出口道有车外,其余都没有进入该出口道的车辆,逆向可变车道出口车辆清空后,逆向可变车道信号灯变绿,逆向可变车道开启时间应在相交直行前一相位(相交方向的左转或者对向直行车辆)之后,并且保证出口道能够清空该相位放行的车辆。令清空长度为L逆+L交叉口,L逆为逆向可变车道的长度(m),L交叉口为使用逆向可变车道出口道功能车辆通过交叉口的长度(m)。假设相交直行为绿灯时,相交直行前一相位的车辆以匀速从交叉口驶向出口道,速度为V开(m/s),可通过实地测量取平均值。则逆向可变车道在相交直行绿灯开启t开时间后开启:
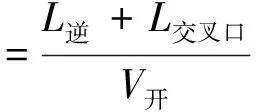
(1)
1.2.2 等待过程
等待过程,车辆逐渐进入逆向可变车道,此时逆向可变车道的车辆受主信号的控制。
1.2.3 离开过程
进入逆向可变车道的信号关闭过早,不能充分利用左转相位时间资源,影响逆向可变车道的通行能力,关闭过晚将导致逆向车道不能腾空,与下一相位对向直行或者相交左转车辆形成冲突。为保证逆向可变车道由进口道功能转化为出口道功能,在左转信号灯变红之前需要清空逆向可变车道上左转的车辆,最后一辆进入逆向可变车道的车辆到驾驶出逆向可变车道的时间为t关(s),距离为L逆(m),视为匀速运动,速度为V关,可通过实地测速取平均值确定具体数值,逆向可变车道信号绿灯相比该左转信号绿灯结束至少要提前t关:
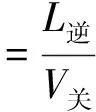
(2)
根据以上叙述,可用信号灯时间变化过程描述逆向可变车道车辆的运行过程,如图3。
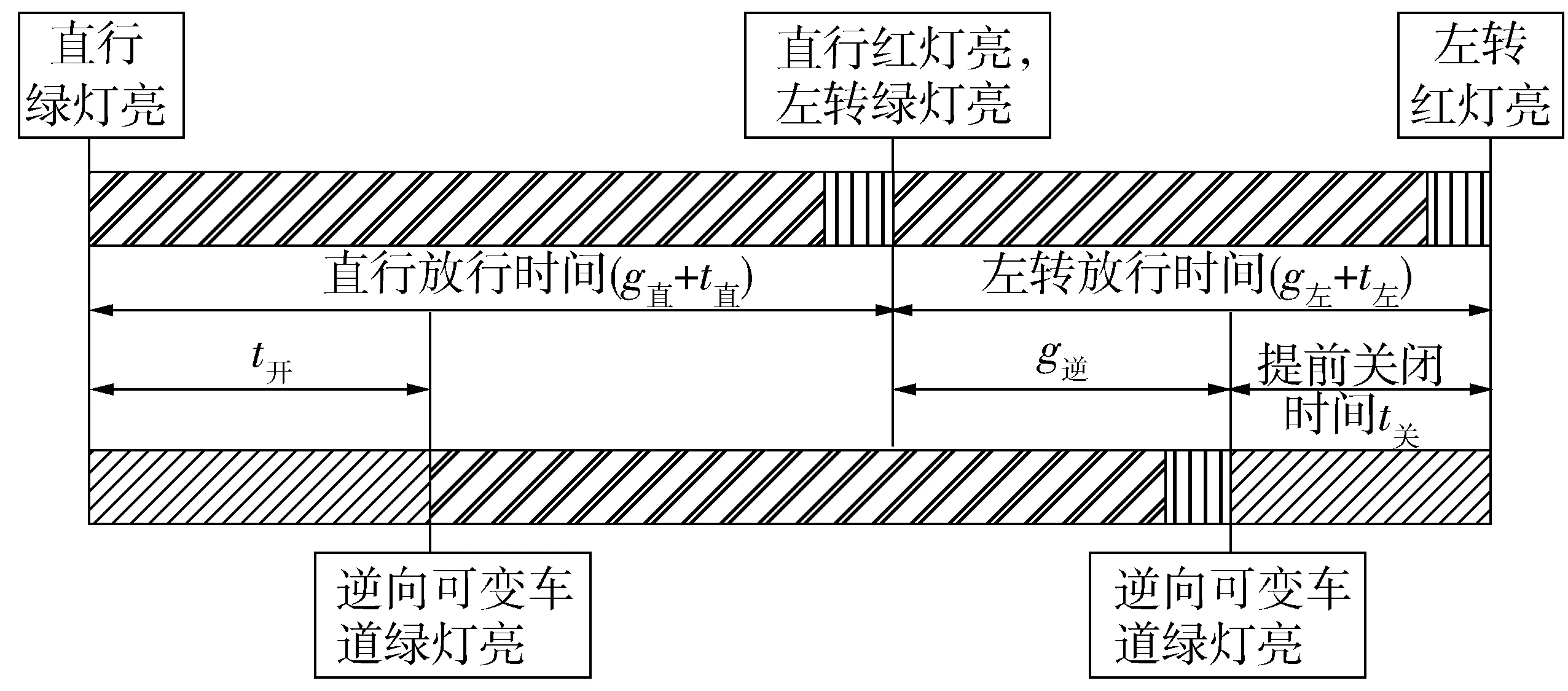
图3 逆向可变车道信号控制过程Fig. 3 Reversing variable lane signal control process
在直行相位绿灯开启t开时间后,逆向可变车道绿灯开启,左转相位红灯开启t关时间前逆向可变车道红灯开启,逆向可变车道的有效绿灯时间g逆=g左+t开-t关。
2 基于NSGA-Ⅱ算法的信号配时优化模型
2.1 通行能力
饱和流率法是计算信号控制交叉口通行能力的主流方法,是采用饱和流率乘以绿信比的方法计算信号控制交叉口的通行能力[11],采用饱和流率实测法中的车头视距法。该方法首先记录各排队车辆通过停止线的车头时距,然后剔除最初几辆车的数据以避免绿灯初损失时间的影响,最后取平均车头时距的倒数即为饱和流率。某车道组的通行能力可表述为
(3)
式中:CA为所要计算车道组的通行能力;h为计算车道组对应的实测车头视距;g为计算车道组对应的有效绿灯时间;C为整个交叉口的周期;N为计算车道组对应的车道数。
交叉口的通行能力CA总等于所有车道组的通行能力之和:
(4)
式中:CAk为第k个车道组的通行能力;n为交叉口所有进口道划分的车道数。
2.2 交叉口延误
交通流间断而损失的车辆行驶时间,目前应用最广的交叉口延误计算方法为美国道路通行能力手册HCM2010的数学分析模型[12]。车道组控制延误等于均匀延误、增量延误和初始排队延误之和,而交叉口延误等于交叉口所有车道组的延误之和。车道组每车的延误估算公式如式(5):
d=d1+d2+d3
(5)
式中:d为控制延误;d1为均匀延误;d2为增量延误,d3为初始排队延误。
d1和d2计算公式见式(6)和式(7),假设初始没有排队,d3=0。
(6)
(7)
式中:C为周期;g为有效绿灯时间;T为分析持续的时间;X为车道组的饱和度;K为感应控制的增量延误修正,对于固定周期K取0.5;I为按上游信号灯车辆换道和调节的增量延误修正(对于独立交叉口I取1);CA为车道组的通行能力。
将逆向可变车道单独作为一个车道组,其他交叉口车道按照正常的车道组分组,逆向车道组的通行能力和延误公式分别为
(8)
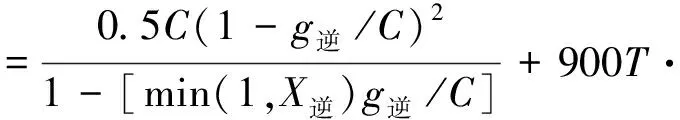
(9)
2.3 目标函数
在一定的道路条件下,信号控制交叉口的通行能力受信号周期时长的影响。在正常的周期时长范围内,周期时长越长,通行能力越大,但车辆延误及油耗等也随之增长。交叉口通行能力越大,延误越小,交叉口运行状况越好。对设置逆向可变车道交叉口的信号配时优化是根据各个相位各车道组的交通量,以各相位有效绿灯和逆向可变车道的长度为变量,使得目标函数交叉口通行能力越大,车辆交叉口控制延误越小。
(10)
约束条件
(11)
条件①:最短绿灯gmin限制,必须保证行人在绿灯时间内能通过在信号交叉口,最短绿灯时间与步行速度vp、人行道长度Lp有关,见约束条件①。
条件②:信号周期等于各个进口道有效绿灯gi与总延误L之和,见约束条件②。
条件③:对于非饱和的车道组,避免浪费绿灯时间,第i个车道组饱和度xi下限大于0.7,为避免出现拥堵,饱和度上限应小于0.9,对于过饱和车道组,饱和度上限可以大于1,见约束条件③。
2.4 NSGA-Ⅱ算法设计
针对通行能力最大和延误最小的双目标模型,NSGA-Ⅱ是目前运用较好的多目标进化算法之一[13],它降低了非劣排序遗传算法的复杂性,解集收敛性好,运行速度快,为其他多目标优化算法提供参考。NSGA-Ⅱ算法是K.DEB等[14]于2002年在 NSGA 的基础上提出的,相比NSGA算法:采用了快速非支配排序算法,计算复杂度降低;使准Pareto域中个体能扩展到整个Pareto域,并均匀分布,保持了种群的多样性;引入了精英策略,扩大了采样空间,防止最佳个体的丢失,提高了算法的运算速度和鲁棒性。过程如下(图4):
步骤1:参数设定,设种群规模为N,t为当前进化代数,T为最大进化代数,TF为适应度函数值偏差。
步骤2:编码,常用的编码有二进制、格雷码和实数编码等。根据所研究的通行能力和延误选择实数编码。
步骤3:初始种群P0,t=0,随机产生初始种群。
步骤4:选择,使用锦标赛选择法从Pt中选择N个个体进入交配池,选择操作是基于序值和拥挤距离的,对于两个个体,序值小的个体被选中,当序值相同时,拥挤距离越大,种群多样性越好,选中拥挤距离大的个体。并对交配池中的个体实施交叉和变异操作,产生新种群Ht,与Pt合并为Rt。
步骤5:对Rt实施环境选择,生成下一代种群Pt+1,维持种群规模为N。
步骤6:结果判断,判断是否满足种群结束条件T,如果t 图4 NSGA-Ⅱ算法的计算流程Fig. 4 Calculation process of NSGA-Ⅱ algorithm 选取重庆市龙山路—天竺路交叉口为分析对象,交叉口为标准的四路十字交叉,南进口直左车道和右转车道,东进口左、直、直右车道,北进口左、直、右车道,西进口左、直、直右车道,交叉口几何现状如图5,单车道宽度为3.5 m,相位相序如图2中的方案(2),交叉口参数见表1。 表1 龙山路-天竺路交叉口参数Table 1 Parameters of longshan-tianzu intersection 图5 交叉口几何现状Fig. 5 Shape of intersection 该交叉口为四相位定时控制交叉口,南进口直左车道左转流量较大,饱和度大于1,南进口道满足设置逆向可变车道的条件。不改变现有相位相序,先将交叉口划分车道组,假定每个相位的损失时间都为4 s,以4个相位的有效绿灯时间和逆向可变车道长度为自变量,交叉口通行能力最大(为方便编程处理,将以通行能力负值最小)和分析持续时间T=0.25 h的交叉口控制延误最小为优化目标,利用NSGA-Ⅱ算法进行优化,设置种群规模为100,遗传代数200,交叉概率0.7,变异概率0.1,求得30组pareto解及最优目标,如图6。图6表明,交叉口通行能力越大延误越大,交叉口通行能力最大和延误最小不能在同一个点达到,考虑到此交叉口各个车道组的交通量较大,饱和度都较高,信号配时方案选取一组通行能力相对占优的pareto解,其取值为g南进口=35 s、g东进口=40 s、g北进口=20 s、g西进口=60 s、l逆=38.3 m,作为交叉口控制的优化方案,并进行计算。 图6 NSGA-Ⅱ算法计算结果Fig. 6 Calculation result of NSGA-Ⅱ algorithm 上述优化结果中,g南进口=35 s、g东进口=40 s、g北进口=20 s、g西进口=60 s、l逆=38.3 m表示当南、东、北、西进口道有效绿灯时间分别为35、40、20、60 s,逆向可变车道长度为38.3 m时,交叉口通行能力尽可能大而交叉口控制延误尽可能小。同时开始设定每个相位的损失时间都为4 s,包括黄灯3 s,则南、东、北、西进口道有绿灯时间分别为36、41、21、61 s,红灯时间分别为139、134、154、114 s。 对交叉口做了交叉口优化设计和信号配时优化,针对具有左转相位和左转流量较大的进口道,设置了逆向可变车道,并对逆向可变车道重新进行配时优化。表2对现状控制方案、设置逆向可变车道方案与设置逆向可变车道后,运用NSGA-Ⅱ算法优化控制配时方案,通行能力与交叉口控制延误结果进行对比。 表2 交叉口优化前后对比Table 2 Comparison of intersections before and after optimization 对于左转流量较大的,交通量方向分布不均衡的单点信号控制交叉口,当交通量趋于饱和时,在交叉口的几何空间许可的条件下,设置逆向可变车道对信号设计与交通优化有较明显的效果。信号方案的优化可建立一个以相位有效绿灯时间、饱和度和逆向可变车道长度为约束条件,交叉口平均延误时间最小、交叉口通行能力最大的双目标函数模型,并运用NSGA-Ⅱ双目标优化算法,对目标函数进行优化,得到一组通行能力目标相对占优的信号配时。以重庆某交叉口为例,对比现状配时方案、逆向车道设置后(配时不变)以及基于逆向可变车道设计信号配时优化方案(配时改变)3种状况下的通行能力和延误,得出逆向可变车道设计并通过优化方法得到的方案能够提升交叉口的通行能力和降低控制延误。案例中以15 min的数据进行分析,增加逆向车道方案后通行能力提高232 pcu/h,交叉口控制延误降低98 s。采用优化模型对配时进行优化,交叉口通行能力进一步提升,交叉口控制延误显著降低。 参考文献(References): [1] WEBSTER F V.TrafficSignalSettings[R].London:HMSO,1958. [2] 杨晓光,杨佩昆.信号灯控制交叉口停车线车辆延误模拟算法[J].同济大学学报(自然科学版),1993,21(1):67-73. YANG Xiaoguan,YANG Peikun.Simulative models on signalized intersection stop-line delay[J].JournalofTongjiUniversity(NaturalScience),1993,21(1):67-73. [3] 杨锦冬,杨东援.城市信号控制交叉口信号周期时长优化模型[J].同济大学学报(自然科学版),2001,29(7):789-794. YANG Jindong,YANG Dongyuan.Optimized signal time model in signaled intersection[J].JournalofTongjiUniversity(NaturalScience),2001,29(7):789-794. [4] 孙超,徐建闽.基于Synchro的单点交叉口信号8配时优化研究[J].公路交通科技,2009,26(11):117-122. SUN Chao,XU Jianmin. Study on traffic signal timing optimization for single point intersection based on synchro software system[J].JournalofHighwayandTransportationResearchandDevelopment,2009,26(11):117-122. [5] 李丽丽,姚荣涵,周红媚,等.渠化可变导向车道交叉口预设信号配时优化模型[J].吉林大学学报(工学版),2015,45(1):75-81. LI Lili,YAO Ronghan,ZHOU Hongmei,et al.Optimization model for pretimed signals at an intersection with reversible approach lanes[J].JournalofJilinUniversity(EngineeringandTechnologyEdition),2015,45(1):75-81. [6] 李瑞敏,唐瑾.过饱和交叉口交通信号控制动态规划优化模型[J].交通运输工程学报,2015,15(6):101-109. LI Ruimin,TANG Jin.Traffic signal control optimization model of over saturated intersection based on dynamic programming[J].JournalofTrafficandTransportationEngineering,2015,15(6):101-109. [7] 首艳芳,徐建闽.信号交叉口多目标动态决策模型及其优化方法[J].公路交通科技,2012,29(11):92-97. SHOU Yanfang,XU Jianmin.Multi-objective dynamic decision-making model of signalized intersection and its optimization method[J].JournalofHighwayandTransportationResearchandDevelopment,2012,29(11):92-97. [9] ZHAO J,MA W,ZHANG H,et al.Increasing the capacity of signalized intersections with dynamic use of exit lanes for left-turn traffic[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard,2013,2355:49-59. [10] 商振华.逆向可变车道在城市平面交叉口中的设置方法[D].西安:长安大学,2013. SHANG Zhenhua.SettingMethodoftheReverseVariableLaneintheUrbanIntersections[D] .Xi’an:Chang’an University,2013. [11] 杨晓光,赵靖,马万经,等.信号控制交叉口通行能力计算方法研究综述[J].中国公路学报,2014,27(5):148-157. YANG Xiaoguang,ZHAO Jin,MA Wangjin,et al.Reviews on calculation method for signaled intersection capacity[J].ChinaJournalofHighwayandTransport,2014,27(5):148-157. [12] MANUAL H C.HCM2010[M].Washington,D.C.:Transportation Research Board,2010. [13] 王超学,田利波.一种改进的多目标合作型协同进化遗传算法[J].计算机工程与应用,2016,52(2):18-23. WANG Chaoxue,TIAN Libo.Improved cooperative coevolutionary genetic algorithm for multi-objective[J].ComputerEngineeringandApplications,2016,52(2):18-23. [14] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multi objective genetic algorithm:NSGA-Ⅱ[J].IEEETransactionsonEvolutionaryComputation,2002,6(2):182-197.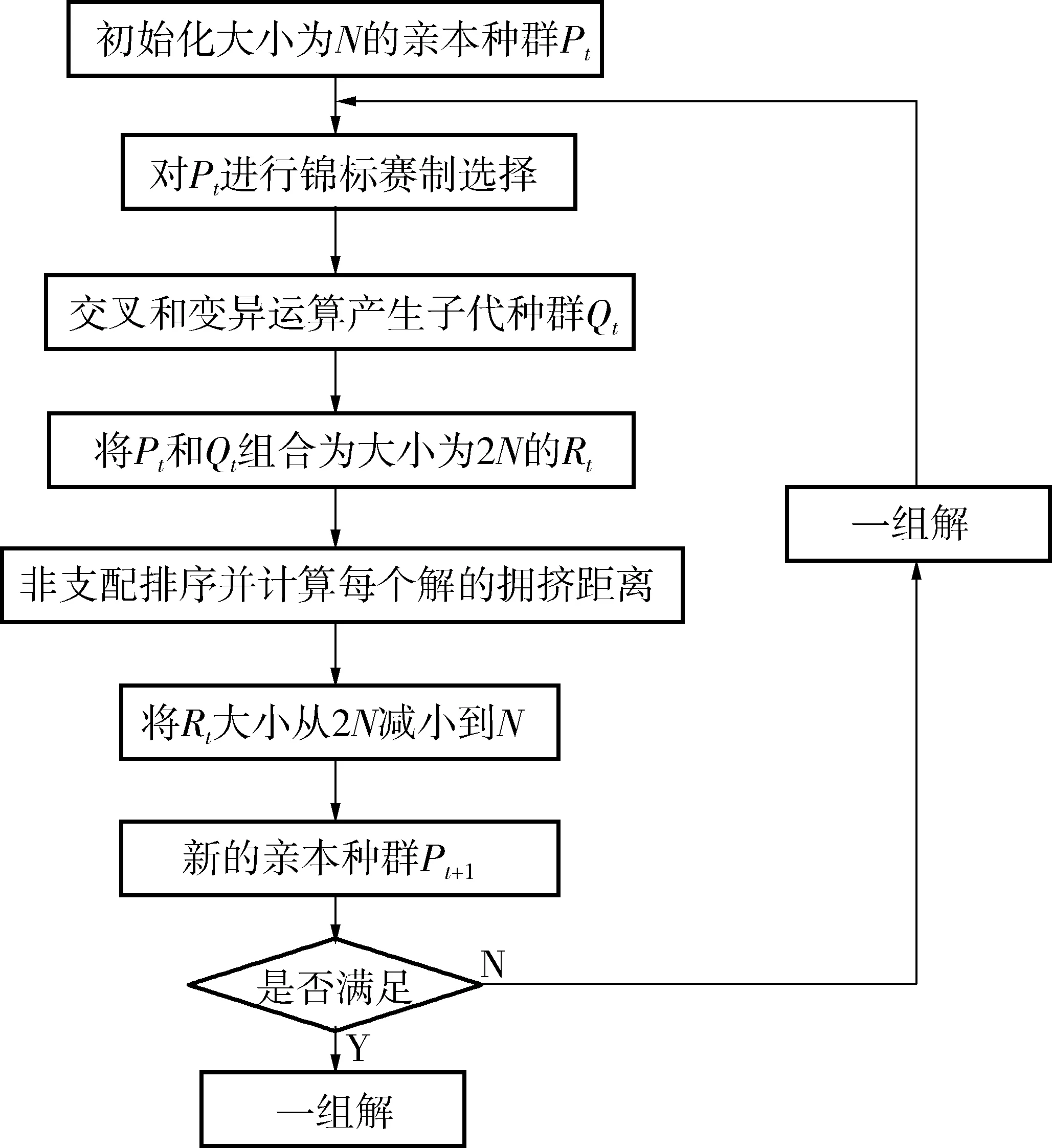
3 实例运用
3.1 路口现状

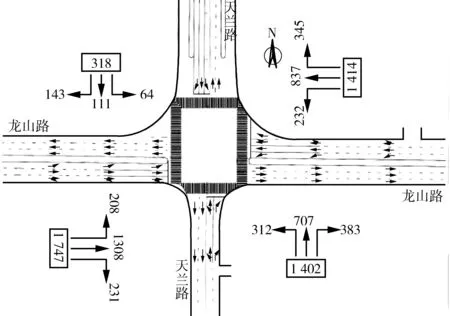
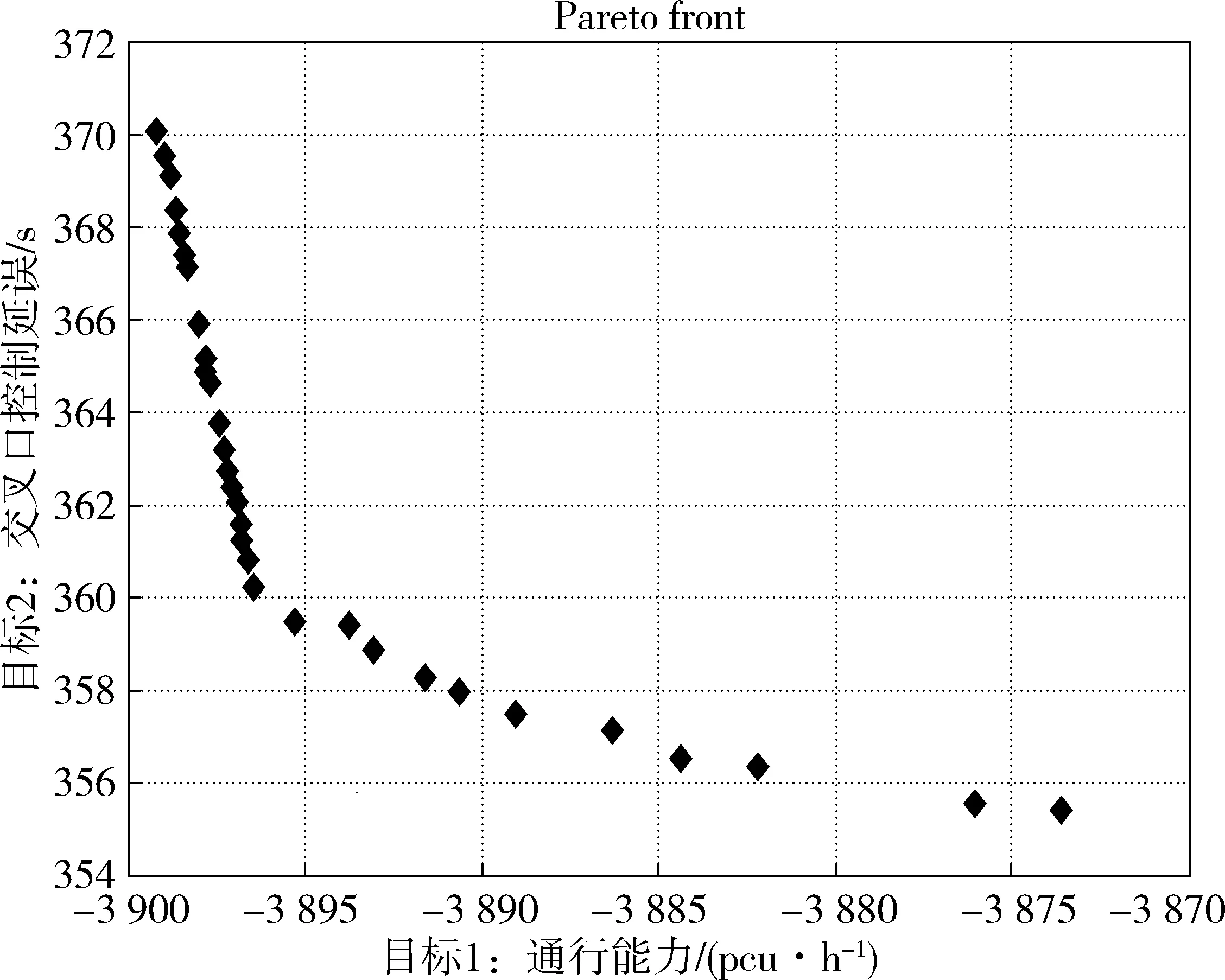
3.2 结果分析

4 结 语
