考虑管冷的大体积混凝土水化热初期温度场研究*

李之达，孙绪涛

(武汉理工大学 交通学院，湖北 武汉 430063)

1 工程概况

武汉市四环线武湖至吴家山段，位于四环线北部区域，也称武汉北四环线。北四环TJ-06-1工段，设府河特大桥一座，起讫里程K57+407～K58+619 (0#—29#墩)，长1 212 m，其中主桥及跨堤连续梁桥一共3联。跨堤桥1#、2#、22#、23#承台尺寸为横桥向15.2 m×顺桥向8.2 m×高3 m，采用C30混凝土，单个承台混凝土体积373.92 m3。混凝土结构物实体最小几何尺寸不小于1 m的大体量混凝土，或预计会因混凝土中胶凝材料水化引起的温度变化和收缩而导致有害裂缝产生的混凝土，称之为大体积混凝土[1]。所以该桥墩承台属于大体积混凝土构件，需要进行水化热温度场研究及监测。

2 温度场计算原理

2.1 水管冷却等效热传导方程

大体积混凝土浇筑完成后的温度场可视为以水化热作用作为内部热源的空间不稳定温度场，其温度场的计算实际上是对空间不稳定温度场的热传导方程在给定的初始条件和边界条件下的求解。实际工程中，混凝土表面与空气或水接触，在冷却过程中，水管冷却的作用与外界温度变化的影响是同时存在的，因此，采用水管冷却等效热传导方程计算这种实际的温度场[2-6]，热传导方程为

(1)

a=λ/cρ

(2)

式中：T为混凝土温度，℃；T0为混凝土初温，℃；Tw为冷管入水温度，℃；τ为时间，h；a为导温系数，m2/h；φ(τ)为水冷函数，其表达式形式可参考文献[2] ；θ0为τ→∞时的最终水化热，kJ/kg；φ(τ)为水冷温升函数，根据所选用的绝热温升函数类型计算得到，具体可参考文献[2] ；λ为导热系数，kJ/(m·h·℃)。

2.2 边值条件

满足热传导方程的解有无限多，要确定需要的温度场，还应知道初始条件和边界条件。初始条件为在初始瞬时物体内部的温度分布规律，边界条件为混凝土表面与周围介质(如空气或水)之间温度相互作用的规律[2，7-8]。边界条件可分为4类，笔者主要用到第3类边界条件，即假定经过混凝土表面的热流量与混凝土表面温度T和气温Ta之差成正比，即

q=β(T-Ta)

(3)

其中：

(4)

式中：q为当混凝土与空气接触时，经过混凝土表面的热流量，kJ/(m·h)；n为表面外法线方向。

2.3 热传导方程的有限元解法

考虑上述边界条件，对式(1)在空间域用有限元离散，得

(5)

(6)

(7)

(8)

对式(5)在时间域用后向差分法离散，得到：

([C]+[K]Δτ){T}n+1=[C]n{T}+Δτ{F}n+1

(9)

通过式(9)，利用n时段的节点温度值和热荷载向量{F}即可求出n+1时段的节点温度值。

3 承台温度传感器的布置

承台内从下到上布置3个测试断面，依次为A、B、C断面，如图1(b)。每个断面布置温度传感器7个，分别布置于1/2对角线和1/2宽度范围内，如图1(a)。总计布置21个温度测点。因为混凝土浇筑体的外表温度，宜为混凝土外表以内50 mm处的温度，混凝土浇筑体底面的温度，宜为混凝土浇筑体底面上50 mm处的温度，所以以C断面测点的温度作为承台外表温度，以A断面测点的温度作为承台底面温度。

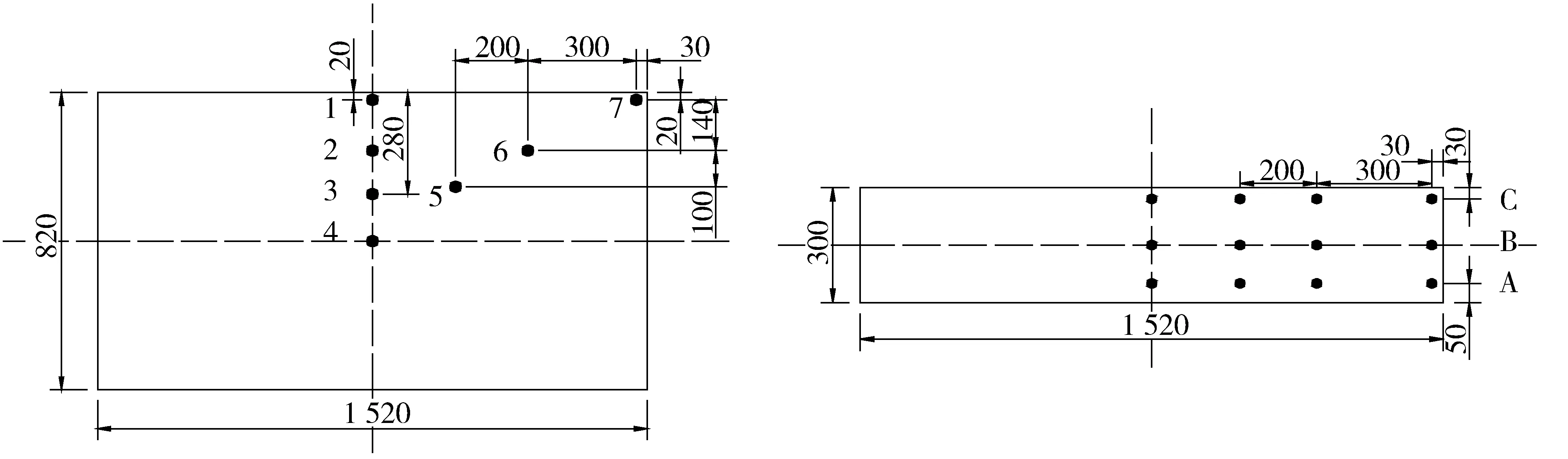
图1 温度传感器布置(单位：cm)Fig. 1 Layout of temperature sensor

4 承台温度场模拟

4.1 参数选取

根据GB 50496—2009《大体积混凝土施工规范》计算得模型中的相关参数。部分参数如表1。

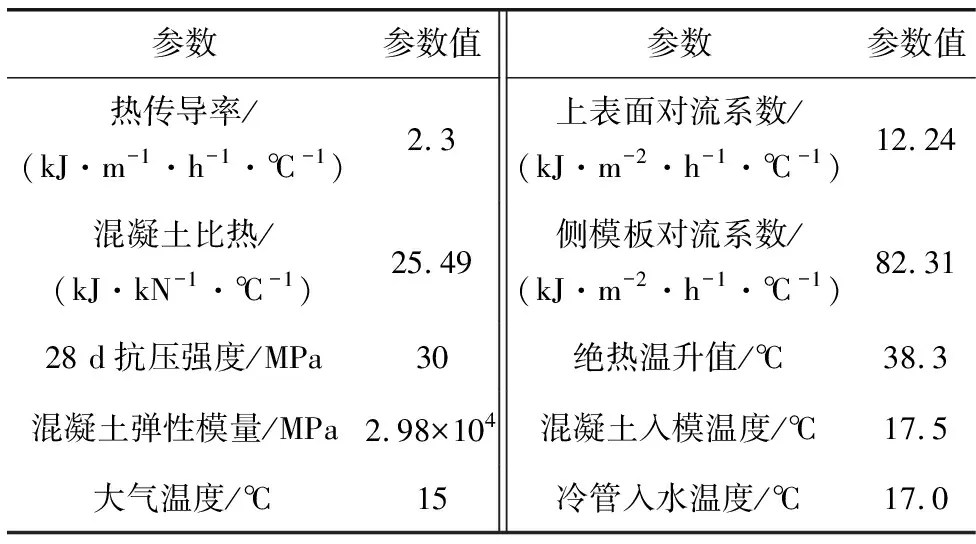
表1 部分参数取值Table 1 The values of several parameters

4.2 承台有限元模型建立

采用Midas/Civil模拟承台温度场，考虑到承台和内部埋设管冷的对称性，取结构的1/2进行分析，原来桩基础采用等效地基处理，如图2。

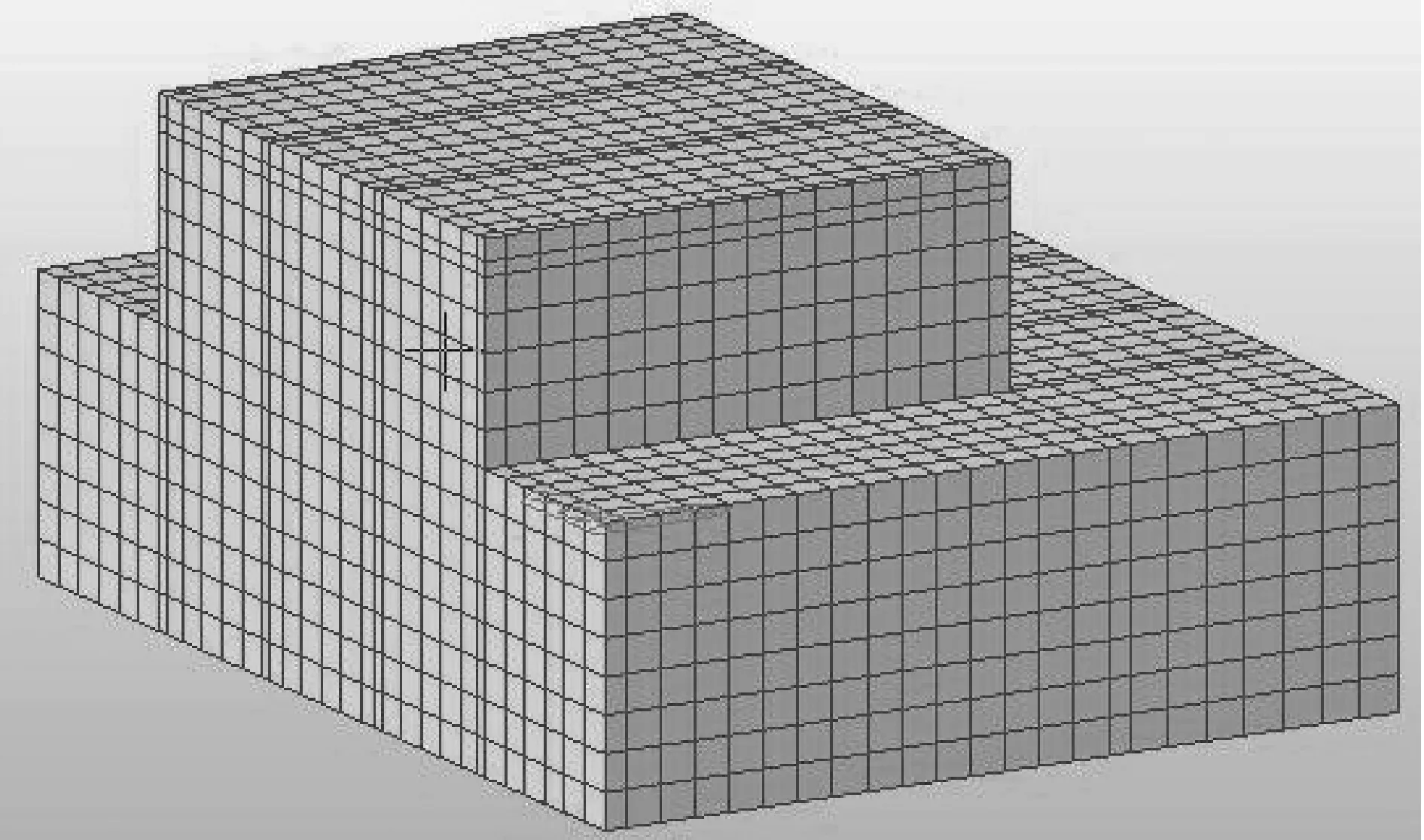
图2 温度场分析模型Fig. 2 Analysis model of temperature field

计算模型单元采用八节点空间等参元，该模型共有9 627个节点，8 128个单元。

4.3 温度场分析

不同龄期承台混凝土的温度场分布云图如图3。3个监测断面各温度测点的温度时程曲线如图4。

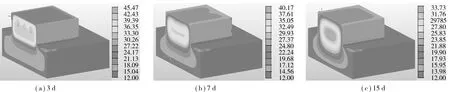
图3 承台温度场云图(单位：℃)Fig. 3 Bearing platform’s temperature field contours

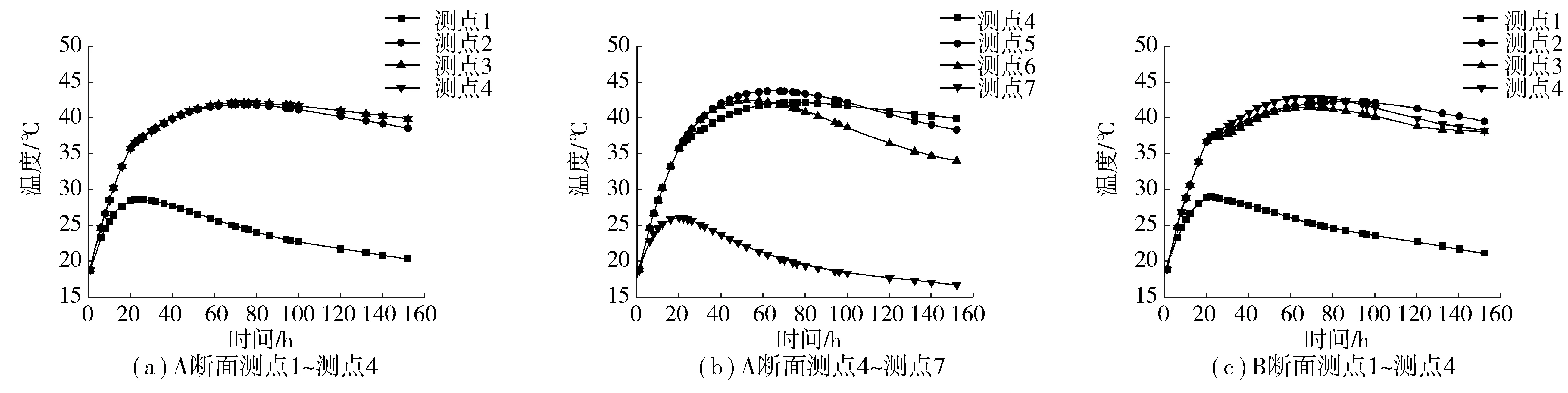
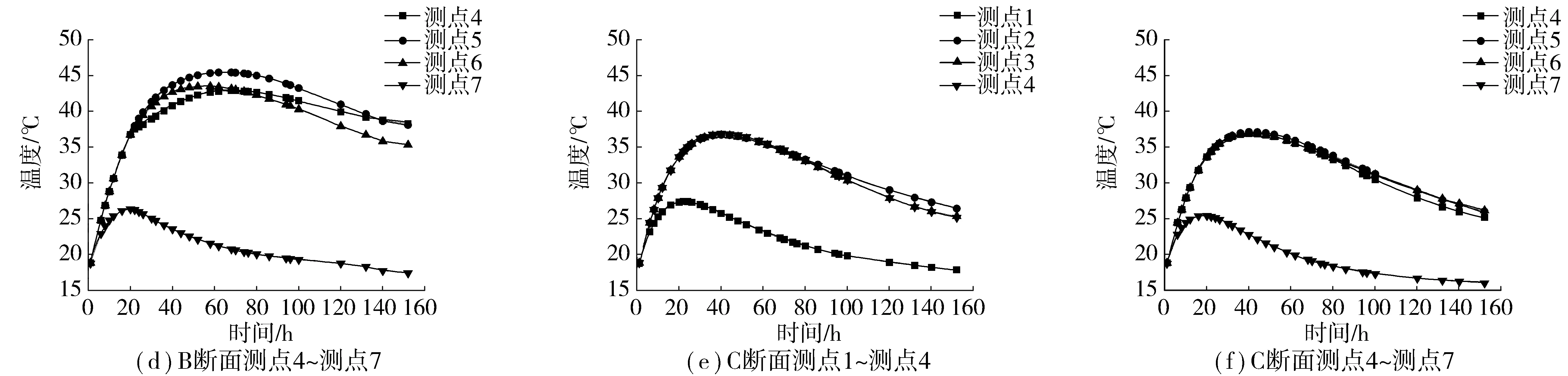
图4 断面测点计算温度时程曲线Fig. 4 Calculated temperature-time curve of measuring points

由图3、图4可得：

1) 因混凝土体积大，导热性差，随着水泥水化作用的进行，承台中心处水化热不断积蓄，温度场急剧变化，承台内部温峰出现在浇筑后60～70 h，最高温度为45.5 ℃。达到温峰后开始降温，冷管在20～120 h通水，所以在120 h之前承台内部温度下降速率大，承台内部最大降温速率为3.1 ℃/d，出现在C断面测点3附近，120 h后停止通水，承台内部开始慢速降温，降温速率小于2.0 ℃/d。

2) C断面测点及A、B断面上的1号、7号测点均靠近承台表面，更易向环境中散热，故温度变化与中心处差别较大，混凝土经急剧升温后，所达到的温度峰值比中心处低，且峰值持续时间短，之后很快进入降温阶段，并在很短的时间内达到较稳定状态。因此，承台表面必须采取充分的保温措施以控制内外温差。

3) 承台上表面温峰出现在第40 h左右，最高温度为37.5 ℃。承台侧面温峰出现在第20 h左右，最高温度为28 ℃。由温度场云图也可看出，承台侧面与上表面温差最高可达9.1 ℃。因为承台上表面覆盖塑料薄膜及土工布，而侧面采用的钢模板未做保温处理，承台侧面可以更快的向环境中散热，所以侧面温峰出现较早且数值低于上表面温峰值。

4) 温度的绝对值并不影响大体积混凝土的开裂，开裂与否主要与内部的温度梯度有关，温度梯度越大，开裂的可能性越高。由温度场云图可看出，承台表面以下1 m范围内的温度梯度较大，内部其他区域温度分布较为均匀。

5 承台温度监测结果

5.1 监测结果

3个监测断面各温度测点的实测温度曲线如图5。

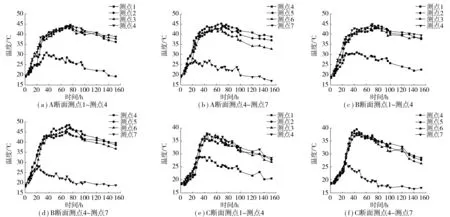
图5 断面测点实测温度曲线Fig. 5 Measured temperature-time curve of measuring points

5.2 结果分析

1) 实测温度时程曲线走势与计算结果基本相符，但在温度数值和温峰出现时间方面有所差别。这是因为计算时采用理论绝热温升曲线，并对相关边界条件适当简化，水流假设为均匀流动，而实际水流是不均匀流动，且实际入水温度随气温有小幅波动，并不是恒定值，同时，现场浇筑混凝土也存在自然条件变化(包括日照、风速变化等)，冷管通水过程中因停电和器械问题而出现数次间断，所以温度场实测值与计算值有差异，实测温度曲线呈锯齿状，而计算温度曲线均十分光滑。实际施工时混凝土由下向上浇筑，上层混凝土迟于底部混凝土开始水化热反应，而在计算时假定混凝土一次浇筑完成，各高度混凝土同时开始水化热反应，所以实测温度曲线与计算温度曲线在温峰出现时间上存在时间差。

2) A断面实测最高温度45.2 ℃，计算最高温度43.8 ℃，计算误差3.1%；B断面实测最高温度48.4 ℃，计算最高温度45.5 ℃，计算误差6.0%；C断面实测最高温度39.6 ℃，计算最高温度37.1 ℃，计算误差6.3%。

3) 承台内部温峰出现在浇筑后70～80 h，与计算结果相比延后约10 h；承台上表面温峰出现在第40 h左右，承台侧面温峰出现在20～25 h，与计算结果基本相符。

4) 由A、B断面测点温度曲线可看出，在0～160 h内，承台温度随龄期的发展经历了升温-缓慢降温-快速降温3个阶段，具有一般大体积混凝土水化热初期温度变化的典型特征。

5) 与A、B断面相比，C断面浇筑较晚，所以在0～20 h，C断面测点温度上升较慢，在25 h左右温度开始急剧上升，因C断面靠近承台表面，向环境中散热速度较快，在达到峰值后随即开始降温，且降温速率较A、B断面大，C断面承台内部最大降温速率为3.4 ℃/d，与C断面计算结果基本相符。

综上所述，温度场的计算误差大小在可接受范围内，所建立的有限元模型可以较好的模拟大体积混凝土水化热初期温度场变化特征，为工程应用提供参考。

6 承台保温加强

由实测温度时程曲线可知，A断面承台内部最大降温速率为3.2 ℃/d，B断面承台内部最大降温速率为2.9 ℃/d，C断面承台内部最大降温速率为3.4 ℃/d，均超出了规范中要求的2.0 ℃/d，并且3个断面上靠近承台表面的1号、7号节点受环境温度影响大，温度曲线波动幅度大，这均说明承台表面保温措施不充分，温度下降过快。由承台混凝土第4 d温度应力云图(图6)也可看出，承台表面拉应力数值超出相应龄期的混凝土抗拉强度标准值，这说明承台表面附近温度梯度过大，从内到外温度变化剧烈，产生了很大的拉应力。因此，有必要对承台加强保温。

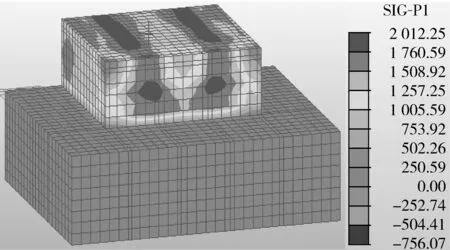
图6 承台第4天温度应力云图(单位：kN/m2)Fig. 6 Bearing platform’s temperature contour on the 4th day

当混凝土表面有模板或保温层时，仍按第3类边界条件计算，可用混凝土表面模板或保温层的放热系数β来等效对流换热系数。

承台上表面保温措施由覆盖1 cm厚土工布加塑料薄膜改为覆盖5 cm厚土工布，计算得其对流系数为2.77 kJ/(m2·h·℃)；承台侧面模板外由不保温改为覆盖4 cm厚土工布，计算得其对流系数为3.46 kJ/(m2·h·℃)。

经计算得承台不同龄期的温度应力云图如图7。

图7 承台温度应力云图(单位：kN/m2)Fig. 7 Bearing platform’s thermal stress contours

将承台表面拉应力超出混凝土相应龄期抗拉强度标准值的区域定义为表面高拉应力区，比较承台加强保温前后表面高拉应力区面积占承台表面积的百分比，如表2。

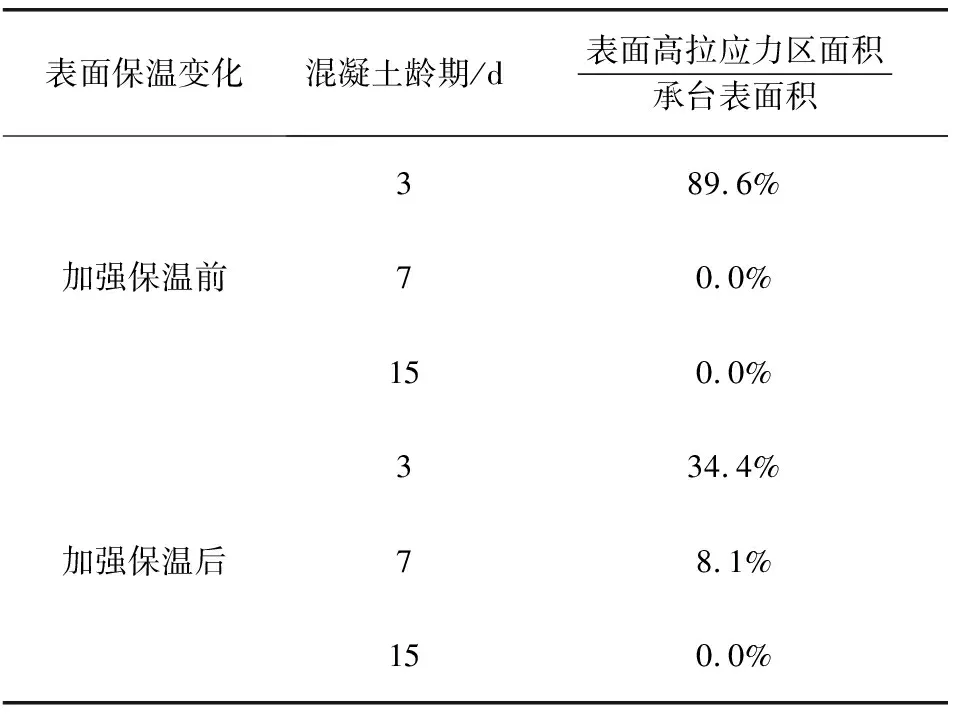
表2 表面高拉应力区面积占比Table 2 Percentage of high tensile stress areas on surface

由图7和表2可看出，承台加强保温后表面拉应力分布得到改善，第3 d时承台表面高拉应力区面积占比由89.6%降至34.4%，且超出混凝土相应龄期抗拉强度标准值的拉应力分布更浅，深度不超过20 cm，考虑到承台表面以下3 cm处布置了直径8 mm的防裂钢筋网片，承台表面开裂的可能性已非常小，但在承台边缘区域仍要注意加强保温和养护。

7 冷管入水温度的影响研究

承台加强保温后，在入水温度为8～30 ℃共21个工况下模拟承台温度场，分析承台最高温度和管边混凝土最大拉应力与入水温度的关系。结果如图8～图10。

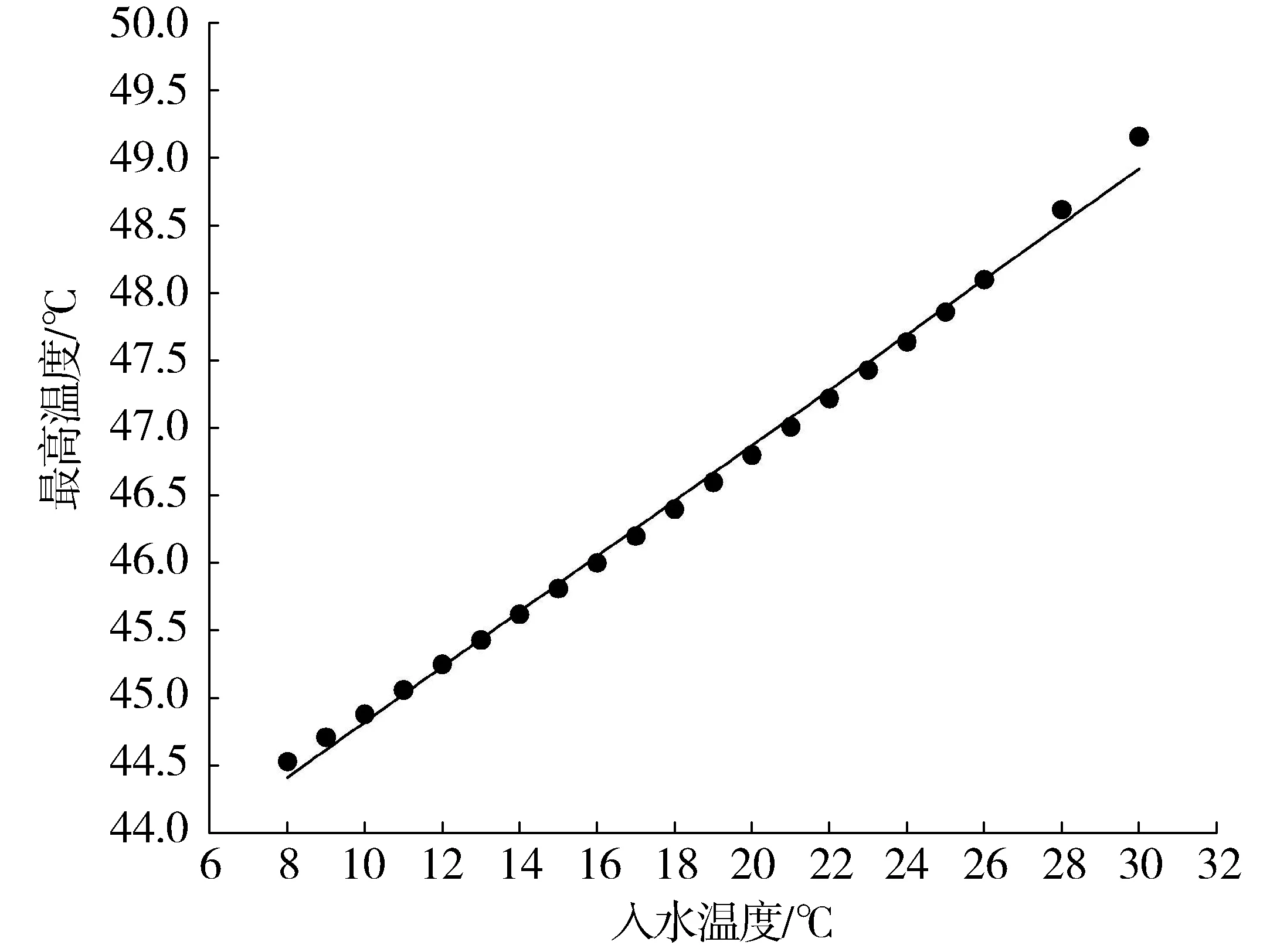
图8 承台最高温度拟合曲线Fig. 8 Fitting curve of bearing platform’s maximum temperature

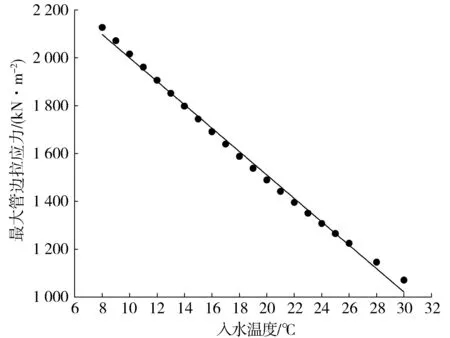
图9 管边最大拉应力拟合曲线Fig. 9 Fitting curve of maximum tensile stress near pipe

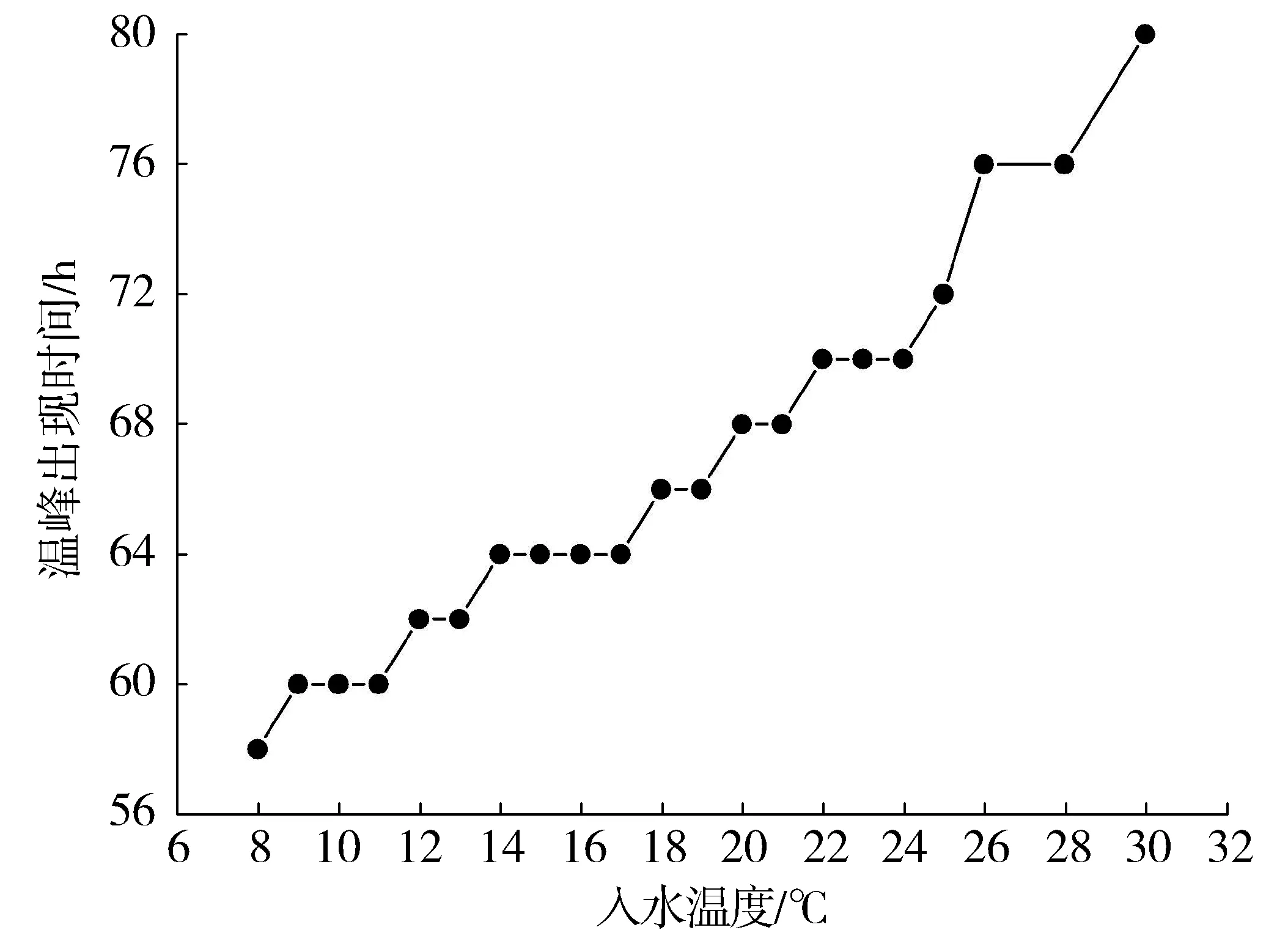
图10 温峰出现时间曲线Fig. 10 Curve of occurrence time of maximum temperature

根据以上结果，降低冷管入水温度可有效降低混凝土内部最高温度，并可在较短时间内使承台达到最高温度进而开始降温，但也有不利影响：在冷管开始通水时，冷管周围混凝土温度急剧下降，形成冷击，由于混凝土结构本身的互相约束，会产生相当大的拉应力。并且在冷管通水后，承台整体温度急剧下降，混凝土徐变不能充分发展，与天然冷却相比，会产生较大的拉应力[2]。

因此，实际工程中冷管入水温度最好可以根据承台内部最高温度做出相应调节。混凝土最高温度通常出现在龄期2～4 d，根据计算结果，管边混凝土最大拉应力也均出现在此期间，应将管边混凝土最大拉应力作为入水温度的控制条件。根据GB 50496—2009《大体积混凝土施工规范》，计算得第3 d时混凝土的抗拉强度是1 207 kN/m2，由图9可知，入水温度在26～27 ℃时可保证最大管边混凝土拉应力不超过混凝土抗拉强度，此时混凝土最高温度与冷管入水温度相差约22 ℃。

所以在冷却初期应充分利用混凝土弹性模量小、徐变大、松弛作用大的优点，可加大通水流量以降低内部高温区的温度，但要将冷却水与混凝土之间的温差控制在22 ℃以内，以防止水管周围混凝土拉应力超过允许拉应力；后期混凝土弹性模量已较高，此时则应降低通水流量，以控制降温速率，防止承台内部出现过大的温度梯度，减小温度应力的不利影响。

8 结 论

笔者结合武汉府河大桥跨堤桥22#承台施工，根据水管冷却等效热传导方程，利用有限元软件模拟承台温度场，并在承台浇筑后进行了持续6 d的温度监测，对比分析有限元计算结果和温度监测结果，得到如下结论：

1) 监测结果和计算结果吻合良好，实测温度时程曲线走势与计算结果基本相符，但在温度数值和温峰出现时间方面有所差别。3个监测断面的温峰值最大计算误差为6.3%，实际温峰出现时间与计算温峰出现时间最大相差约10 h，承台内部最大降温速率计算误差为11.8%，所建立的有限元模型可以较好的模拟大体积混凝土早期水化热温度场变化特征，为工程应用提供参考。

2) 根据实测温度时程曲线和计算所得的温度应力云图可看出，承台表面保温措施不够充分，在对承台侧面添加保温层，对顶面加厚保温层后，按第3类边界条件求得对流换热系数，代入有限元模型中计算，根据所得计算结果，承台加强保温后表面拉应力分布得到改善，在混凝土龄期为第3 d时表面高拉应力区占比由89.6%降至34.4%，超出混凝土相应龄期抗拉强度标准值的拉应力分布更浅，深度不超过20 cm。

3) 对冷管入水温度的影响做出研究，承台温度场最高温度和冷管入水温度呈线性正相关，冷管入水口附近的管边最大拉应力和冷管入水温度呈线性负相关，随着入水温度升高，温峰出现时间会向后推迟。降低冷管入水温度可有效降低混凝土内部最高温度，并可在较短时间内使承台达到最高温度进而开始降温，但也有不利影响。实际工程中冷管入水温度最好可以根据承台内部最高温度做出相应调节，将冷却水与混凝土之间的温差控制在22 ℃以内。

参考文献(References)：

[1] 中国冶金建设协会.GB 50496—2009 大体积混凝土施工规范[S].北京：中国计划出版社，2009：7-8.

China Metallurgical Construction Association.CodeforConstructionofMassConcrete[S].Beijing：China Planning Press，2009：7-8.

[2] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京：中国电力出版社，1999.

ZHU Bofang.TemperatureStressandTemperatureControlofMassConcrete[M].Beijing：China Electric Power Press，1999.

[3] 朱伯芳，王同生，丁宝瑛，等.水工混凝土结构的温度应力与温度控制[M].北京：水利电力出版社，1976.

ZHU Bofang，WANG Tongsheng，DING Baoying，et al.TemperatureStressandTemperatureControlofHydraulicConcreteStructure[M].Beijing：Water Resources and Electric Power Press，1976.

[4] 朱伯芳.有内部热源的大块混凝土用埋设水管冷却的降温计算[J].水利学报，1957(4)：87-106.

ZHU Bofang.Calculation of temperature in mass concrete with internal source of heat，cooled by embedded pipes[J].JournalofHydraulicEngineering，1957(4)：87-106.

[5] 朱伯芳.考虑水管冷却效果的混凝土等效热传导方程[J].水利学报，1991，22(3)：28-34.

ZHU Bofang.Equivalent equation of heat conduction in mass concrete considering the effect of pipe cooling[J].JournalofHydraulicEngineering，1991，22(3)：28-34.

[6] 朱伯芳.考虑外界温度影响的水管冷却等效热传导方程[J].水利学报，2003，34(3)：51-56.

ZHU Bofang.The equivalent heat conduction equation of pipe cooling in mass concrete considering influence of external temperature[J].JournalofHydraulicEngineering，2003，34(3)：51-56.

[7] 朱伯芳.论混凝土坝的水管冷却[J].水利学报，2010，41(5)：505-513.

ZHU Bofang.On pipe cooling of concrete dams[J].JournalofHydraulicEngineering，2010，41(5)：：505-513.

[8] 朱伯芳.混凝土坝水管冷却仿真计算的复合算法[J].水利水电技术，2003，34(11)：47-50.

ZHU Bofang.Compound methods for computing the effect of pipe cooling in concrete dams[J].WaterResourcesandHydropowerEngineering，2003，34(11)47-50.