正规矩阵的性质注记*
2018-07-03何锐琴任芳国
何锐琴,任芳国
(陕西师范大学数学与信息科学学院,陕西 西安 710062)
正规矩阵的性质和特征在矩阵理论及其实际应用中具有重要作用.王桂松等[1]研究了矩阵的奇异值与特征值的关系,R Grone等[2]、L Elsner等[3]研究了正规矩阵的若干等价条件.笔者拟借助文献[4-6]和正规矩阵的基本性质、特征[7-9],并利用矩阵的特征值与奇异值的关系[10-12],来获取有关正规矩阵的新性质.

引理1[1]设A和B为任意n阶复方阵,λ(AB)为AB的任一特征值,σi(A)和σi(B)分别为A和B的奇异值,且σ1(A)≥σ2(A)≥…≥σn(A),σ1(B)≥σ2(B)≥…≥σn(B),则σn(A)σn(B)≤|λ(AB)|≤σ1(A)σ1(B).
引理2[5]设A为正规矩阵当且仅当A的奇异值为{|λ1|,…,|λn|}.
引理3[4]如果A可对角化,那么与A相似的任一对角矩阵的各对角元必须是A的具有适当重数的特征值.
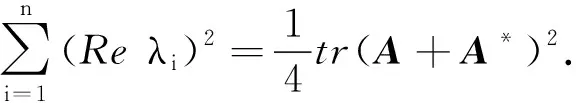
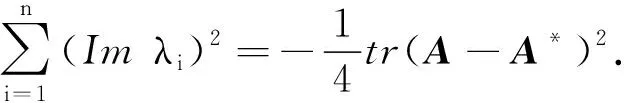
定理1设A是正规矩阵,则对于任意的酉矩阵U(U∈Mn),

定理2设A是一个n阶方阵,则对于任意的单位向量x(x∈Cn),|(Ax,x)|2≤(|A|2x,x).此外,A正规当且仅当|(Ax,x)|≤(|A|x,x),∀x∈Cn.
证明|(Ax,x)|≤‖Ax‖·‖x‖,而‖x‖=1,(|A|2x,x)=(A*Ax,x)=(Ax,Ax)=‖Ax‖2,于是|(Ax,x)|2≤(|A|2x,x).


当n>2时,由归纳法可得.
定理3设A是一个正规矩阵,若存在正整数k使得Ak=I,则A是酉矩阵.

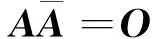


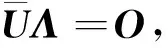
定理5设A是一个非奇异矩阵,M=A-1A*,则A是正规矩阵当且仅当M是酉矩阵.
证明必要性.因为A是正规矩阵,所以
MM*=A-1A*(A-1A*)*=A-1A*A(A-1)*=A-1AA*(A*)-1=I,
M*M=(A-1A*)*(A-1A*)=A(A-1)*A-1A*=AA-1(A-1)*A*=I,
从而M是酉矩阵.
充分性.由M是酉矩阵有M*=M-1,即(A-1A*)*=(A-1A*)-1,故A(A-1)*=(A*)-1A,左乘A*,右乘A*,即A*A=AA*,从而A是正规矩阵.
定理6A正规等价于存在一个置换σ(σ∈Sn),使得δ(A)={αj+iβσ(j)|j=1,…,n}.
证明必要性.若A正规,则A的特征向量是H和K的特征向量,即存在同一个酉矩阵U,使得

推论1A正规等价于Reδ(A)={α1,…,αn}.
定理7A正规等价于Imδ(A)={β1,…,βn}.

定理8A正规等价于存在一个置换σ(σ∈Sn),使得δ(A)={ujρσ(j)|j=1,…,n}.
证明必要性.若A是正规矩阵,则由引理2可知结论成立.充分性.A*A=P*V*VP=P*P=P2,故A的奇异值为{ρ1,…,ρn}.因为U是酉矩阵,所以|uj|=1,|δ(A)|={ρ1,…,ρn},可知结论成立.
推论2A正规等价于mod(δ(A))={ρ1,…,ρn}.
定理9AB*和BA*都是正规矩阵当且仅当存在酉矩阵V和W(V,W∈Mn),使得A=VΣW*和B=VΛW*(其中Σ,Λ∈Mn,是对角矩阵).
证明必要性.只要考虑A=Σ是非负矩阵又是对角矩阵的情形.将Σ的相同对角元排在一起,不妨设ρ1>ρ2>…>ρr,即
由ΣB*是正规矩阵有
ΣB*BΣ*=BΣ*ΣB*.
(1)
比较(1)式两边的(1,1)元素,得
(2)
由B*Σ是正规矩阵有
B*ΣΣ*B=Σ*BB*Σ.
(3)
比较(3)式两边的(1,1)元素,得
(4)



充分性.由A=VΣW*,B=VΛW*,A*B=WΣ*ΛW*,B*A=WΛ*ΣW*,得(A*B)(A*B)*=WΣ*ΛΛ*ΣW*(A*B)*(A*B)=WΛ*ΣΣ*ΛW*.因为Σ,Λ是对角矩阵,所以(A*B)(A*B)*=(A*B)*(A*B).同理可得B*A是正规矩阵.
定理10设A是厄密特矩阵,B是斜厄密特矩阵,C=A+B,则下列条件等价:(ⅰ)C是正规矩阵;(ⅱ)AB=BA;(ⅲ)AB是斜厄密特矩阵.
证明首先证明(ⅰ)⟺(ⅱ).C正规⟺CC*=A2+BA-AB-B2=A2-BA+AB-B2=C*C⟺AB=BA.其次证明(ⅱ)⟺(ⅲ).AB=BA⟺(AB)*=B*A*=-BA=-AB.因此这3个条件互相等价.
定理11设A,B(A,B∈Mn)是给定的方阵,若A⊗B是正规矩阵,则B⊗A也是正规矩阵.
证明因为B⊗A=PT(A⊗B)P=P*(A⊗B)P,所以若A⊗B是正规矩阵,则B⊗A也是正规矩阵.
参考文献:
[1] 王桂松,吴密霞,贾忠贞.矩阵不等式[M].北京:科学出版社,2006:23-56.
[2] GRONE ROBERT,JOHNSON CHARLES R,SA EDUARDO M,et al.Normal Matrices[J].Linear Algebra and Its Applications,1987,87:213-225.
[3] ELSNER L,IKRAMOV KH D.Normal Matrices:An Update[J].Linear Algebra and Its Applications,1998,285(1/2/3):291-303.
[4] HORN ROGER A,JOHNSON CHARLES R.Matrix Analysis[M].Cambridge:Cambridge University Press,1985:47-80.
[5] HORN ROGER A,JOHNSON CHARLES R.Topics in Matrix Analysis[M].Cambridge:Cambridge University Press,1991:67-89.
[6] ZHANG Fuzhen.Matrix Theory:Basic Results and Techniques[M].Berlin:Spinger,2011:26-76.
[7] SUI Xuefang,GONDOLO PAOLO.Factorizations into Normal Matrices in Indefinite Inner Product Spaces[J].Linear Algebra and Its Applications,2016,516(17):143-166.
[8] MEHL CHRISTIAN,RODMAN LEIBA.Classes of Normal Matrices in Indefinite Inner Products[J].Linear Algebra and Its Applications,2001,336(1/2/3):71-98.
[9] BLEHER PAVEL M,KUIJLAARS ARNO B J.Orthogonal Polynomials in the Normal Matrix Model with a Cubic Potential[J].Advances in Mathematics,2012,230(3):1 272-1 321.
[10] CHAU LING-LIE,ZABORONSKY OLEG.On the Structure of Correlation Functions in the Normal Matrix Model[J].Communications in Mathematical Physics,1998,196(1):203-247.
[11] RUHE AXEL.Closest Normal Matrix Finally Found[J].BIT Numerical Mathematics,1987,27(4):585-598.
[12] HOFFMAN A J,WIELANDT H W.The Variation of the Spectrum of a Normal Matrix[J].Duke Mathematical Journal,1953,20(1):37-39.
