一组非奇异H-矩阵的新判据*

张林娟，莫宏敏

(吉首大学数学与统计学院，湖南 吉首 416000)

H-矩阵是特殊矩阵中最重要的一类矩阵，在计算数学、经济数学、物理学电力系统理论和控制论中都有广泛的应用.笔者拟在文献[1-4]的基础上给出一组判定非奇异H-矩阵的方法.

1 相关定义

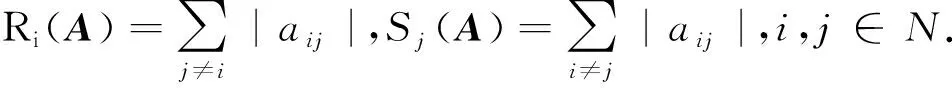
定义2[5]设A=(aij)n×n∈Cn×n，若存在α∈(0，1]，对于∀i∈N，有|aii|>αRi(A)+(1-α)Si(A)，则称A为严格的α-对角占优矩阵；若存在正对角矩阵D使得AD为严格的α-对角占优矩阵，则称A为广义的α-对角占优矩阵.

为了叙述方便，引入下列划分：

N1={i∈N:0<|aii|=αRi(A)+(1-α)Si(A)}，

N2={i∈N:0<|aii|<αRi(A)+(1-α)Si(A)}，

N3={i∈N:|aii|>αRi(A)+(1-α)Si(A)}.

显然，N=N1⊕N2⊕N3.

定义

2 主要结果及其证明

引理1[6]设A=(aij)∈Cn×n，若A为广义的α-对角占优矩阵，则A为非奇异H-矩阵.

引理2[7]设A=(aij)∈Cn×n，若A为不可约的α-对角占优矩阵，或A为具有非零元素链的α-对角占优矩阵，则A为非奇异H-矩阵.

定理1设A=(aij)∈Cn×n，若存在α∈(0，1]，对于∀i∈N2，有

(1)

则A为非奇异H-矩阵.

证明由r和δi(A)的定义可知δi(A)≤r，i∈N3且0≤r<1.对于∀i∈N1，记

对于∀i∈N2，记

αRi(A)+(1-α)Si(A)>Pi(A)i∈N1.

(2)

设

(3)

(4)

构造正对角矩阵X=diag(x1，x2，…，xn)，其中

令B=(bij)n×n=AX，对于∀i，j∈N，有bij=xjaij.现只要证明B为严格的α-对角占优矩阵即可.

又由N3的定义可知，对于∀i∈N3，有

于是对于∀i∈N3，有

即|bii|>αRi(B)+(1-α)Si(B).

综合(ⅰ)—(ⅲ)可知，对于∀i∈N，有|bii|>αRi(B)+(1-α)Si(B),即B为严格的α-对角占优矩阵.由B=AX可知A为广义的α-对角占优矩阵，再由引理1可知A为非奇异H-矩阵.

定理2设A=(aij)∈Cn×n，A不可约，若存在α∈(0，1]，对于∀i∈N2，有

(5)

且至少有1个不等式是严格成立的，则A为非奇异H-矩阵.

证明因为A不可约，所以存在正对角矩阵X使得AX不可约.令B=(bij)n×n=AX，bij=xjaij，∀i，j∈N，则B也不可约.

下面证明B为不可约的α-对角占优矩阵.因为对于∀i∈N2，(5)式中至少有1个不等式严格成立，不妨设j∈Jk⊂N2，所以

构造正对角矩阵X=diag(x1，x2，…，xn)，其中

(ⅰ)对于∀i∈N1，有|bii|>αRi(B)+(1-α)Si(B).

(ⅱ)对于∀i∈N2Jk，有

对于∀i∈Jk⊂N2，有

(ⅲ)对于∀i∈N3，有

(1-α)δi(A)Si(A)>(1-α)(1-δi(A))Si(A)≥0.

综合(ⅰ)—(ⅲ)可知，对于∀i∈N，有|bii|≥αRi(B)+(1-α)Si(B)，B不可约且至少有1个不等式严格成立，即B为不可约的α-对角占优矩阵.由引理2可知B为非奇异H-矩阵，再由引理1可知A为非奇异H-矩阵.

定理3设A=(aij)∈Cn×n，若存在α∈(0，1]，满足以下条件：

且对于∀i∈K(A)，存在非零元素链aij1aj1j2…ajk-1jk使得jk∈NK(A)；

(ⅱ)对于∀i∈N2，有

则A为非奇异H-矩阵.

证明同定理1，略.

3 数值实例

设

取α=1，根据文献[1],N的划分为N1=Ø，N2={1，4}，N3={2，3，5}.因a11=5，a22=100，a33=100，a44=15，a55=30,故R1(A)=10，R2(A)=92，R3(A)=94，R4(A)=22，R5(A)=6.于是，

无法用文献[1]中的定理1进行判定.

无法用文献[5]中的定理1进行判定.

由定理1可判定A为非奇异H-矩阵.

参考文献：

[1] 黄延祝.非奇H矩阵的简捷判据[J].计算数学，1993，15(3):318-328.

[2] 江 如.广义对角占优矩阵的新判据[J].华南师范大学学报(自然科学学版)，2010(1): 24-27.

[3] 高慧敏，陆 全，徐 仲，等.非奇H-矩阵的一组含参数迭代判定准则[J].高校应用数学学报，2012，27(4):439-448.

[4] 刘建州，吕振华，李 林，等.一组非奇异H-矩阵的实用判据[J].湖南文理学院学报(自科版)，2015，27(2):3-4；13.

[5] 江 如.非奇异H-矩阵的新判据[J].工程数学学报，2011，28(3)：393-400.

[6] 李继成，张文修.H矩阵的判定[J].高等学校计算数学学报，1999，21(3)：264-268.

[7] 孙玉祥.广义对角占优矩阵的充分条件[J].高等学校计算数学学报，1997，19(3):216-223.