人参小气候因子对净光合强度影响的线性回归分析

赵红梦，刘馨蔓，刘春明，杜宇静

人参是名贵中药材，具有极高的药用价值。近年来，大面积的人工栽培人参已成为人参市场的主要来源，模拟自然环境的林下栽培是一个不断探索的过程，因此，研究影响人参小气候因子及其这些因子对净光合强度等的影响是一个很重要的问题。聂绍荃、何双等[1]用原始数据建立了回归模型对此问题进行研究，赵红梦等[2]对影响人参小气候因子进行了主成分分析[3]，将影响人参小气候的多个因子用主成分表示,减少影响因子的个数，又不会减少信息量。本文主要利用原始数据和主成分得分分别建立回归模型，并对两种结果作对比分析。

1 模型的建立

根据聂绍荃、何双等[1]给出的1号观测点数据可知，此原始数据共有6个变量，X1为气温、X2为光强、X3为空气相对湿度、X4为5 cm地温、X5为10 cm地温、X6为15 cm地温，规定时间段为8时、10时、12时、14时、16时。 赵红梦等[2]对变量进行主成分分析,对这6个变量得到的两个主成分分别为Z1和Z2，主成分Z1、Z2是气温、光强、空气相对湿度、5 cm地温、10 cm地温、15 cm地温这些变量的线性组合，主成分得分关系式如下：

Z1=0.472X1+0.238X2+0.186X3+0.455X4+0.499X5+0.48X6

Z2=0.169X1-0.635X2+0.655X3-0.311X4-0.015X5+0.204X6

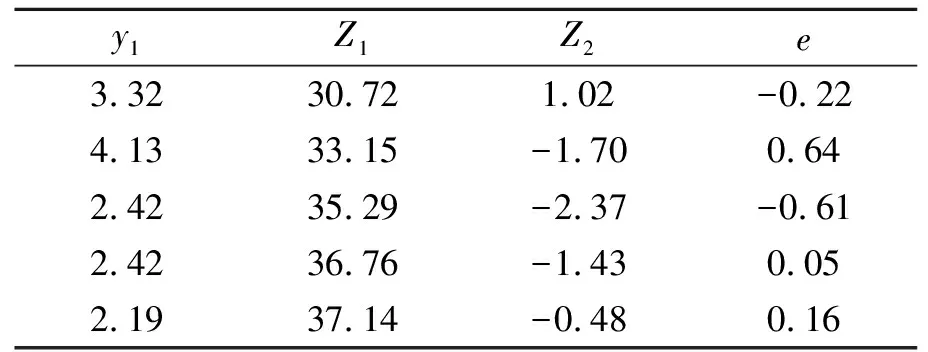
表1 净光合强度、主成分得分值及残差值

根据气温X1、光强X2、空气相对湿度X3、5 cm地温X4、10 cm地温X5、15 cm地温X6的原始数据，可以得到主成分Z1和第二主成分Z2的得分。设净光合强度为y1,y1的原始数据以及第一主成分Z1和第二主成分Z2的得分值见表1。

首先根据以上数据建立线性回归模型:

y1=β0+β1Z1+β2Z2+ε

(1)

2 模型基本假定条件的检验

对多元线性回归模型(1)来说，数据(Zi,y1i),i=1,2,…,5，均满足

y1i=β0+β1Z1i+β2Z2i+εi.

模型基本假定条件为

如果这些假定条件成立，那么只要用最小二乘估计得到模型的参数的估计，然后对回归方程进行显著性检验。但是实际问题中这些假定条件往往不能满足，需要进行检验和处理。首先检验是否存在多重共线性，因为变量Z1和Z2之间简单相关系数很小，所以此线性模型不存在多重共线性。下面对此模型是否存在异方差性和自相关性进行检验。

2.1 异方差性检验

异方差性是指随机误差项的方差不全相等，如果出现异方差性，参数的显著性检验失效，同时回归方程的应用效果不理想，所以要对回归模型(1)的异方差性进行检验，可以根据残差图检验(见图1)。

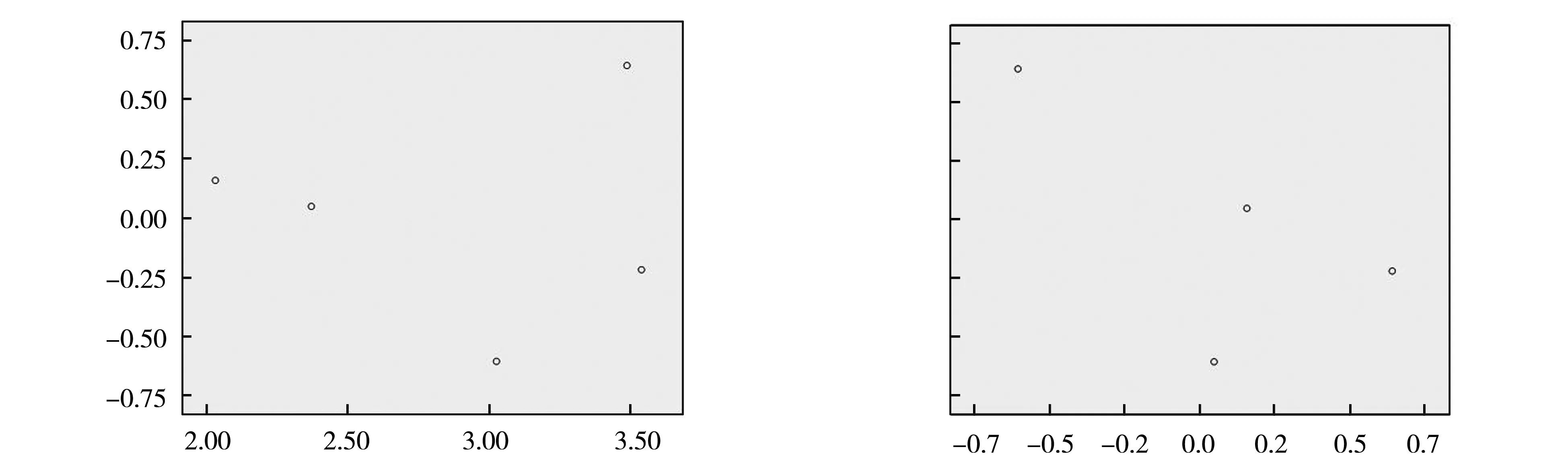
图1 残差图 图2 自相关性检验图

从图1可以看出无异方差性.另外，可以根据等级相关系数进行判定，残差值见表1，用SPSS软件计算|e|与Z1等级相关系数为-0.2,P值为0.747，|e|与Z2等级相关系数为-0.6,P值为0.285，结果显示不存在异方差性。

2.2 自相关性检验

得到回归方程为:

(2)

对回归方程(2)的显著性检验用F检验法，得到的方差分析表如表2。

表2 方差分析表

由表2结果可知，F检验统计量为166.533,P值为0.05,通过了回归模型的显著性检验.

3 结果对比分析

聂绍荃、何双等[1]用原始数据分别建立了两个多元线性回归模型，得到的方程如下：

y1=40.444-0.107X1-0.318X2-53.438X3，
y1=-136.25+9.813X4-29.812X5+29.437X6.

此种方法是人参生理指标净光合强度y1与气温X1、光强X2、空气相对湿度X3建立回归模型,然后人参生理指标净光合强度y1与地温之间建立第二个回归模型,结果显示第一个式子是在不考虑地温的情况下，人参的净光合强度y1与气温X1、光强X2、空气相对湿度X3呈负相关，第二个式子说明不考虑气温、光强和空气相对湿度时人参的净光合强度y1与10 CM地温呈负相关，而与5 CM地温和15 CM地温呈正相关，但是分析时只是分别考虑一部分因素对净光合强度的影响，而没有考虑到其他因素在同一模型中起的

作用。从相关性的角度来看，两种分析方法得到的结论基本是一致的，例如研究y1与气温X1关系，由-0.332Z1+0.045Z2可知X1的系数为-0.08，所以负相关的关系成立，它表示当其它元素不变时气温对净光合强度的影响程度，这样把各种因素综合在一起考虑，分析更全面、更有说服力。

参考文献：

[1] 聂绍荃,何小比,石福臣,周丹. 人参生理生态的研究[J].植物研究,1992(04):417-432.

[2] 赵红梦，刘馨蔓，刘春明,等.影响人参栽培的小气候因子的主成分分析 [J].赢未来，2017(07)： 382-383.

[3] 何晓群.多元统计分析[M].北京：中国人民大学出版社.2015.