转动惯量未知的再入飞行器姿态容错控制
2018-07-03刘伟星耿云海吴宝林
刘伟星,耿云海,吴宝林
(哈尔滨工业大学卫星技术研究所,哈尔滨 150080)
0 引 言
升力式再入飞行器以高超声速再入大气,在整个再入滑翔飞行过程中,大气密度变化剧烈,速度和高度的变化很大,飞行环境恶劣;且大气模型和飞行器再入动力学系统参数都存在着不确定性[1]。因此,再入飞行器的姿态控制系统的设计面临着强耦合、非线性、系统不确定性以及外部干扰等问题的挑战[2]。目前为止,再入飞行器的姿态控制已经得到了较为广泛的研究,主要有滑模控制,模糊控制,最优控制等。文献[3-4]基于X-33模型引入滑模控制,设计了双回路的结构控制系统,该系统分别设计内外环滑模面,将控制系统在滑模运动状态下实现内环角速度和外环姿态角的解耦,并考虑了转动惯量不确定性,外部干扰等因素的影响。耿洁等[5]提出一种最优自适应积分滑模控制方法。文献[6-7]以大升阻比再入飞行器为研究对象,应用非线性动态逆的方法(Nonlinear dynamic inversion,NDI)设计了反馈线性化控制器。由于反馈线性化技术会带来模型误差,而且鲁棒性不强。因此再入飞行器姿态控制系统的研究以非线性控制和自适应控制为主,以增强控制器的鲁棒性和自适应性,如文献[8]将NDI技术和神经网络结合,文献[9]把模型预测控制(Model predictive control,MPC)与反馈线性化(Feedback linear,FBL)结合,文献[10]借鉴线性系统前馈控制思想,提出一种基于模糊前馈的模糊鲁棒跟踪控制方法,文献[11]结合滑模控制和非线性广义预测控制方法,提高了非线性广义预测控制的鲁棒性。
再入飞行器从大气层外进入,恶劣的飞行环境使得飞行器发生故障的概率大大提高,故障会影响飞行器系统的稳定性,可靠性和安全性,甚至使控制系统失效,导致再入任务失败。目前,对再入飞行器的姿态容错控制的研究有一些成果,但还不太成熟。Shen等[12]考虑了传感器的故障,并用T-S建模,设计自适应模糊观测器,能够快速地估计出故障信息,Qi等[13]针对执行器故障运用T-S模糊控制技术设计了再入飞行器的容错控制方案。林常青等[14]利用结合控制分配的方法,当发生故障时,利用冗余的执行器使飞行器安全完成任务。文献[15]设计了自适应动态滑模控制方案,也能较好地应对执行器故障问题。文献[16]针对副翼、升降舵和方向舵几种类型的故障分别设计了积分滑模控制器,但对于严重的故障效果不佳。文献[17]结合被动容错、反步法与滑模控制设计了一种自适应滑模控制,取得了较为满意的效果。
目前再入飞行器的姿态控制器都需要用到转动惯量矩阵,但是转动惯量矩阵的测量会存在着一定的误差,而且在再入的过程中,随着燃料的消耗,防热涂层的烧蚀等过程的进行,飞行器的质量和转动惯量都会发生变化,这会影响需要转动惯量信息的控制系统的性能,因此有必要研究适用于转动惯量不确定性较大,甚至转动惯量未知的情况下的控制方法。针对上述问题,在转动惯量信息未知的条件下,本文针对飞行器再入段发生执行机构故障的情况设计一种姿态容错控制。本文的主要创新之处在于,本文所提的控制方法,控制器中不含转动惯量的信息,对转动惯量信息并不敏感。该控制方法采用反步法的思想:第一步根据运动学模型,先设计期望的参考角速度作为运动学的虚拟控制量,第二步根据动力学设计期望力矩控制器跟踪期望角速度。在第二步的设计中,本文采用的方法不需要转动惯量的信息,将转动惯量,干扰等其它量作为一个综合干扰,用一个估计值对其估计,引入到控制器中。最后对该控制律进行了仿真校验,结果表明该控制律能够应对所提故障,具有较快的收敛速度和较强的抗干扰能力。
1 再入飞行器姿态动力学模型
本文以升力式再入飞行的再入段姿态系统为研究对象,采用文献[9]给出的运动学模型,其模型如下:
(1)
式中:α为攻角,β为侧滑角,σ为倾侧角;θ和φ分别为经纬度,γ和ψ分别为路径角和航向角,在姿态系统中,经纬度变化率,路径角和航向角的变化率都很小;ωE为地球自转角速率,也是一个小量;p,q,r分别为角速度在体坐标系下的三个分量。将运动学写成矩阵的形式,有
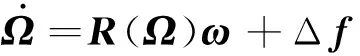
(2)
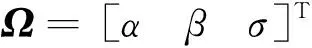
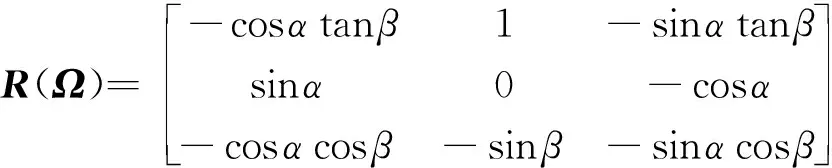
(3)
(4)
姿态动力学模型如下:
(5)
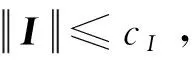
式(2)和式(5)描述了飞行器无故障情况下的模型,考虑执行机构的乘性故障[15]和加性故障得到故障下的动力学模型如下
(6)
式中:ρ(t)=diag(ρ1(t),ρ2(t),ρ3(t))为乘性故障项系数矩阵,表示执行机构剩余的有效执行力,且假设三个通道的剩余有效执行力全不为零,即0<ρi(t)≤1,(i=1,2,3),当ρi(t)=1时,表示无故障,定义其损失的有效执行力为Δρ(t)=E-ρ(t),其中E∈R3×3表示单位矩阵;F∈R3为加性故障项,并假设该项是有界的。当执行机构卡死时,比如舵面卡死在某一个位置,则会产生一个持续的输出,在动力学模型上即表现为加性故障。
2 容错控制律设计
根据上述故障模型,本文的主要目标在于设计一个控制器,使得在发生故障时,控制系统能够使飞行器稳定地跟踪参考气动角。该控制律根据反步法的思想,先设计期望角速度,将期望角速度作为运动学的虚拟控制量,接着设计动力学的控制量,使飞行器跟踪期望角速度。
2.1 期望角速度的设计
令运动学跟踪的参考气动角为Ωc,跟踪误差定义为Ωe=Ω-Ωc,则误差模型如下:
(7)
取虚拟控制量的形式如下:
(8)
式中:K是设计参数,为一个对角阵,且对角线上的元素都大于零,即K是一个正定的对角阵。
注1. 式中Δf为质心旋转运动与质心平移运动耦合的小量,它是一个与轨迹状态量和地球自转角速度相关的函数,由于这些量都是可测的或已知的,因此Δf也是可以计算出来的,多数文献将其当作干扰量,本文将其作为已知量补偿掉。
定理1. 对于系统(7),采用虚拟控制律(8),则定义的气动角跟踪误差Ωe渐近收敛到零。
证.取Lyapunov函数如下:
(9)
对式(9)求导,得
(10)
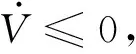
2.2 期望力矩的设计
首先,作如下假设:
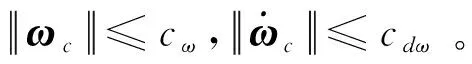
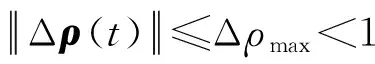
定义角速度误差为ωe=ω-ωc,根据式(6)可以得到误差模型如下:
(11)
根据上述假设,有
(12)
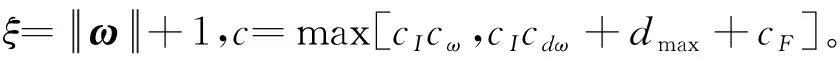
控制力矩指令设计如下:
(13)
(14)
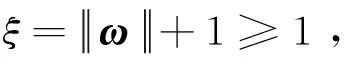
(15)
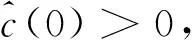
(16)
为了分析所设计的控制系统的稳定性,取Lyapunov函数如下:
(17)
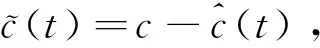
(18)
(19)
根据式(12)和式(19),由式(18)可得
(20)
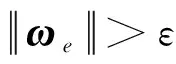
(21)
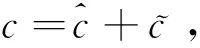
(22)
(23)
因此,只要设计参数kv,κ和α2的关系满足
(24)
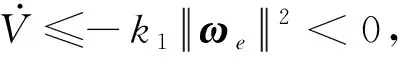
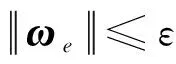
(25)
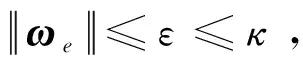
(26)
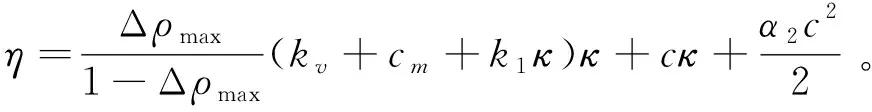
(27)
由此,可以得到如下定理:
定理2. 对于系统(11),采用控制律(13),当选择的控制参数满足式(24)时,则误差最终会收敛到一个包含零点的区域Uω内,且:
(28)
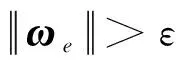
3 仿真校验
本节以X-33飞行器模型作六自由度的再入数学仿真,以验证本文提出的控制方案。六自由度的数学仿真包括质心平移运动和质心旋转运动,质心平移运动模型是制导方面的内容,质心旋转运动是姿态控制的内容。本文对制导内容不做详述,仿真的过程是先求取参考轨迹,采用LQR调节器跟踪参考轨迹得到期望制导指令,然后采用本文所提的控制律跟踪期望制导指令。
X-33飞行器再入过程的转动惯量矩阵为[3]
飞行器再入初始高度为60 km,初始速度为7000 m/s。假设在再入点时的初始角速度为ω(t0)=[0 0 0]T°/s,初始气动角为Ω(t0)=[18° 10° 50°]T,跟踪指令Ωc(t)为六自由度仿真制导回路中生成的制导指令,其中侧滑角的期望值为零。
式(8)中,期望角度的设计参数为K=diag(1,1,1),容错控制其它参数分别为α1=104,α2=10-5,k1=2.5×104以及kv=1.5×104,κ=0.002,Δρmax=0.6。在1000 s处添加常值加性故障F,在80 s处添加的乘性故障ρ(t),ρ(t)和外部干扰d(t)及F的表达式如下
103Nm。
仿真中,初始位置偏差设置如下:
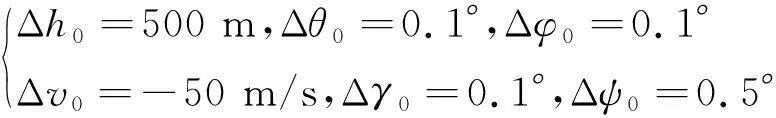
仿真结果图见图1~8。图1中为高度,速度以及经纬度的跟踪轨迹,图中的轨迹与离线规划的轨迹基本重合,本文主要关注点在于对姿态的跟踪,因此与轨迹相关的其它曲线图在此省略。
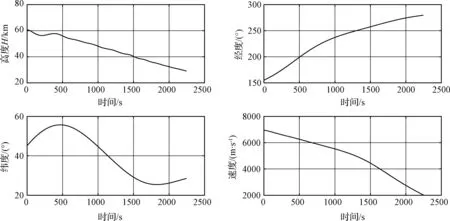
图1 部分轨迹跟踪曲线Fig.1 Part of trajectory tracking state
图2~4为飞行器对制导指令的跟踪曲线,分别为攻角、倾侧角和侧滑角,在仿真中给气动角一个初始误差,从图2~4可以看出,本文设计的姿态控制律可以较快地调整气动角,跟上期望的制导指令,误差在10 s左右就达到较小值。这一点也可以从图5的误差曲线中看出。
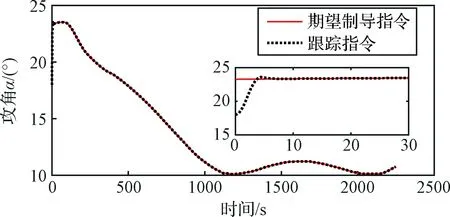
图2 攻角跟踪曲线Fig.2 Attack angle tracking
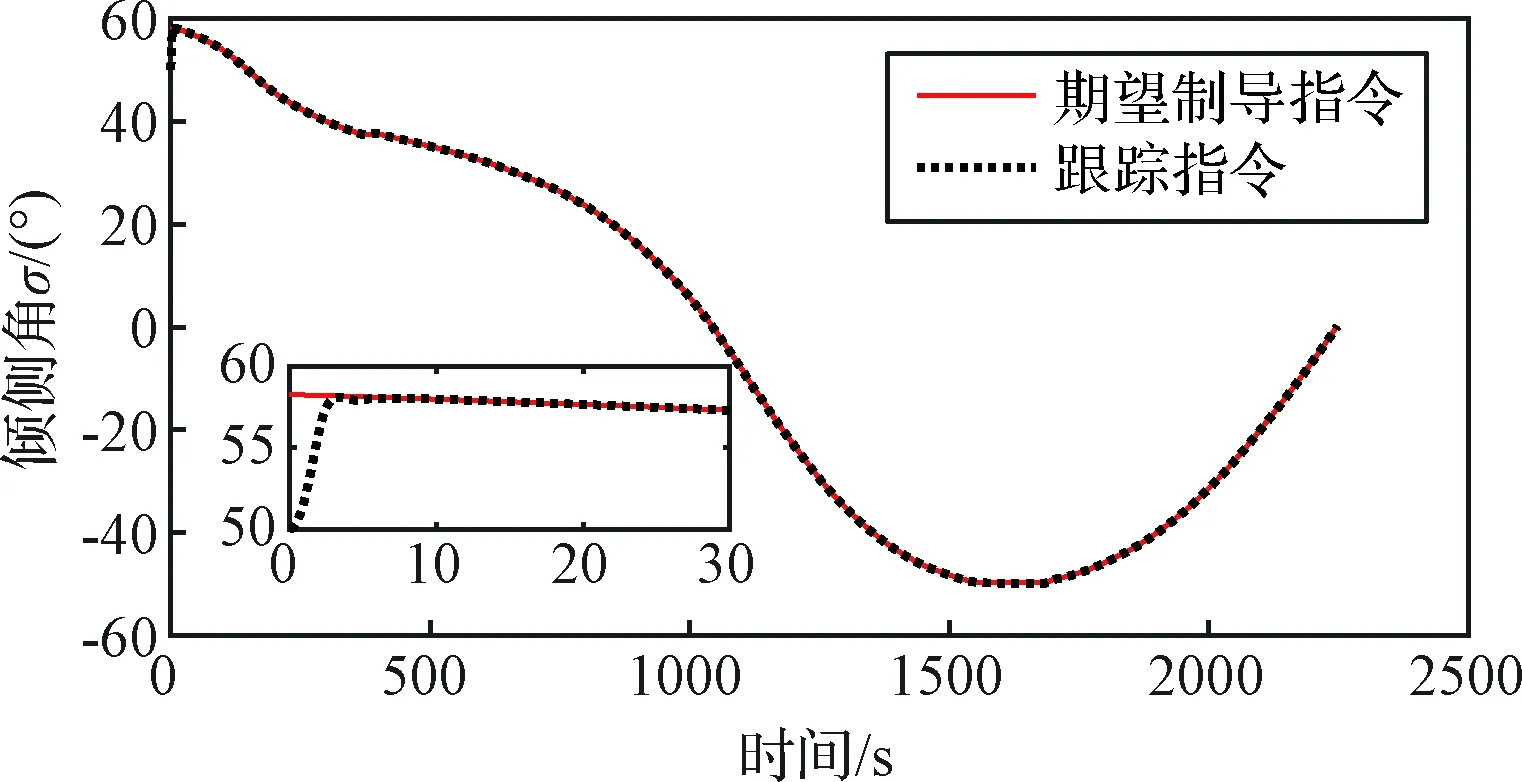
图3 倾侧角跟踪曲线Fig.3 Bank angle tracking
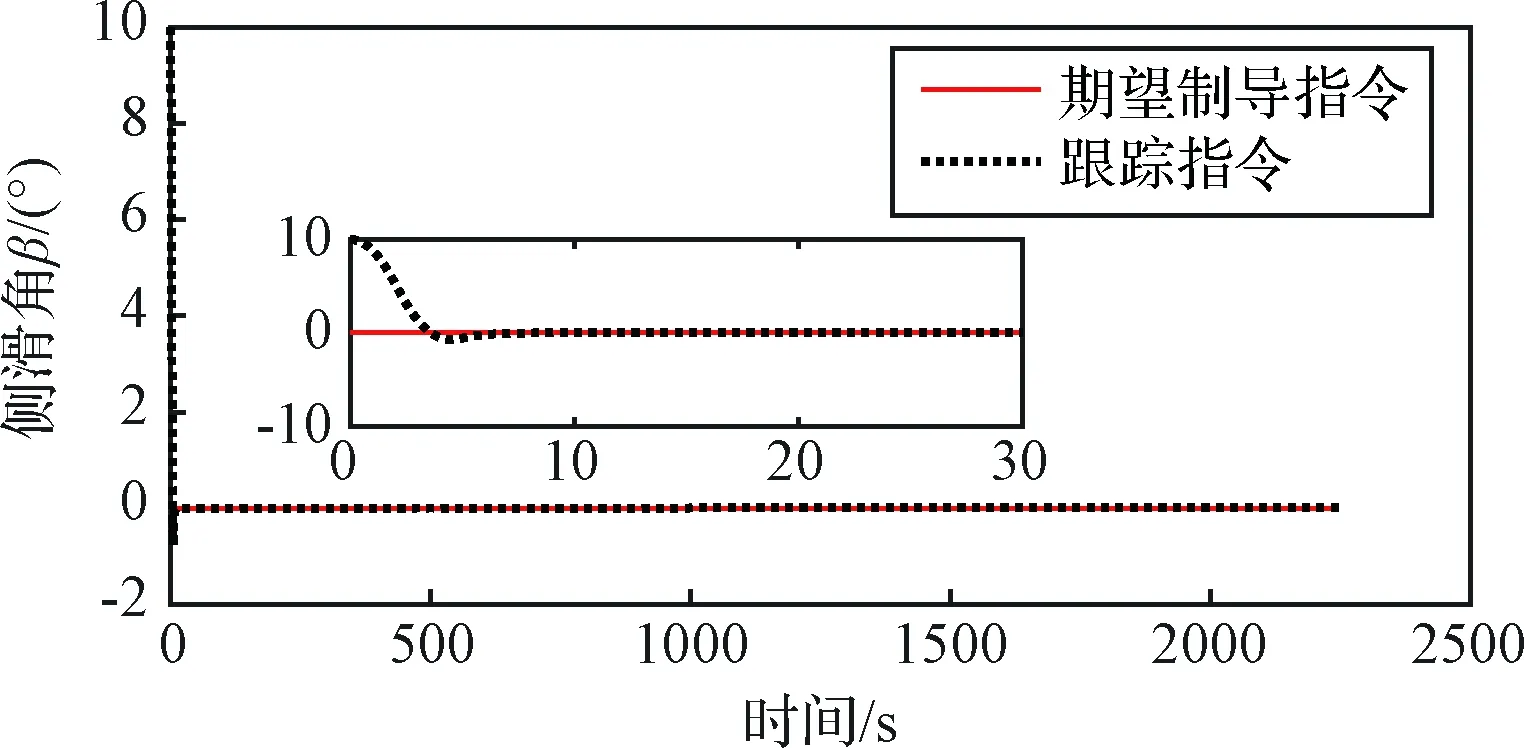
图4 侧滑角跟踪曲线Fig.4 Slide angle tracking
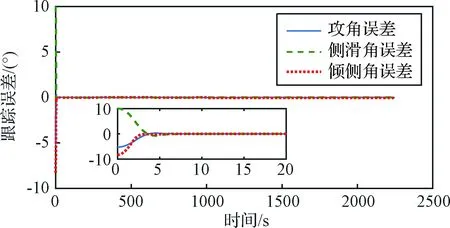
图5 制导指令跟踪误差Fig.5 Attack, bank, and slide angle tracking error
图6为角速度曲线,刚开始有初始误差,角度较大,当跟踪稳定之后,角度的变化比较小,这跟设计的参考轨迹有关。图7为力矩曲线,飞行器的转动惯量比较大,因此所需要的力矩也比较大。由于存在初始误差,在初始阶段需要较大的力矩,收敛之后力矩随着误差的变小而减小。从图7可以看出,在收敛之后,力矩曲线呈现一个周期性的正弦波动,这是因为在仿真中加入的干扰力矩也是一个正弦曲线,与力矩曲线表现的一致,表明本文的控制方案可以很好地抑制干扰力矩。而在80 s处,出现乘性故障之后,所需力矩也会加大,反应速度很快,从而在气动角和角速度上并不会反映出明显的波动。在1000 s时,加入一个常值故障,从图7可以看出,控制器能很好地将该常值补偿掉。图8为自适应参数曲线。
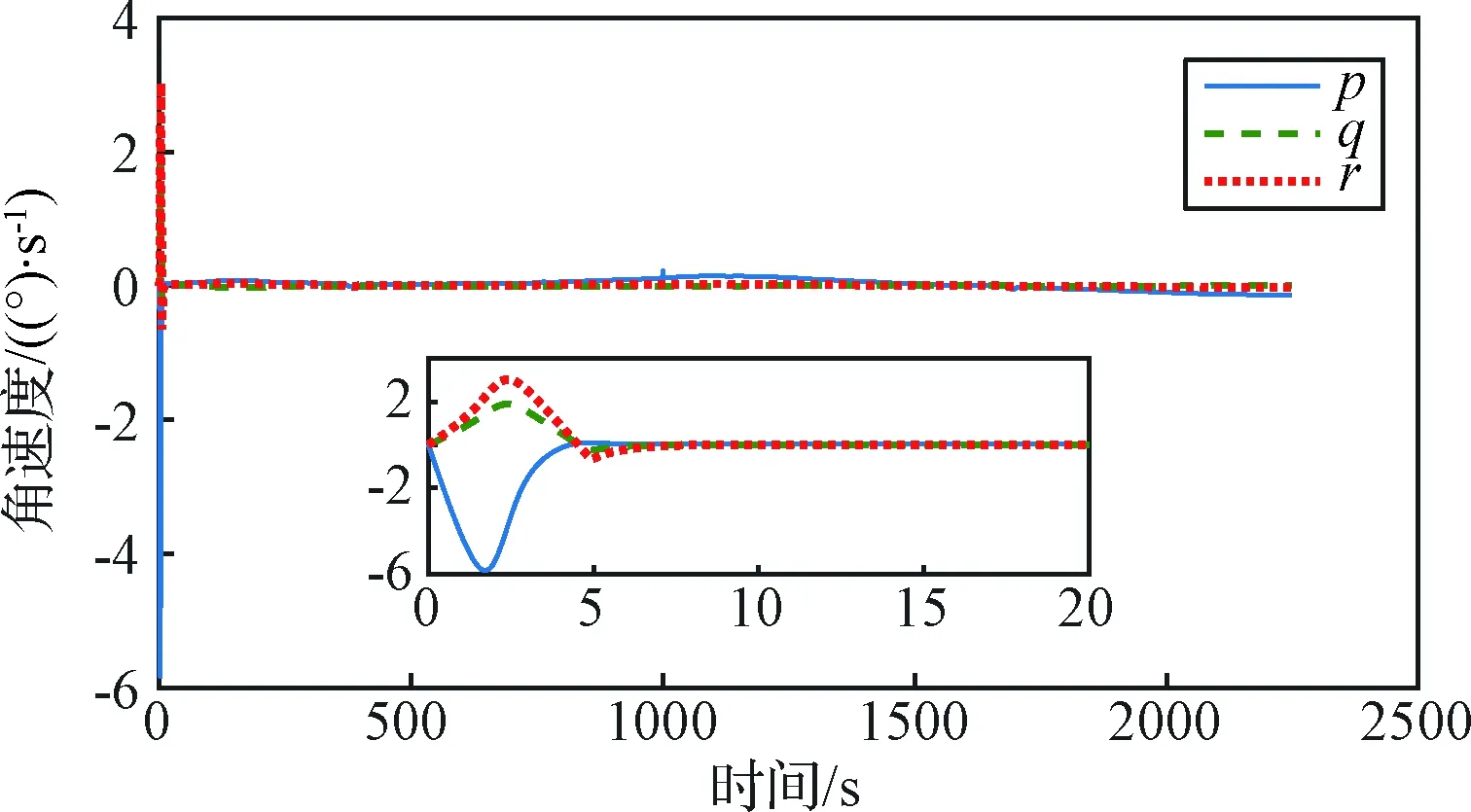
图6 角速度曲线Fig.6 Angular velocity
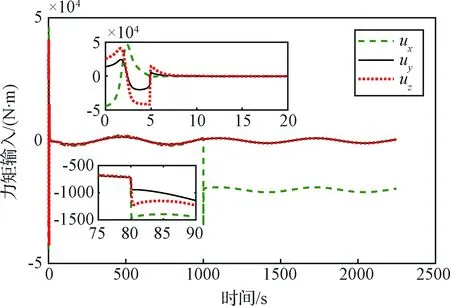
图7 控制输入Fig.7 Control input
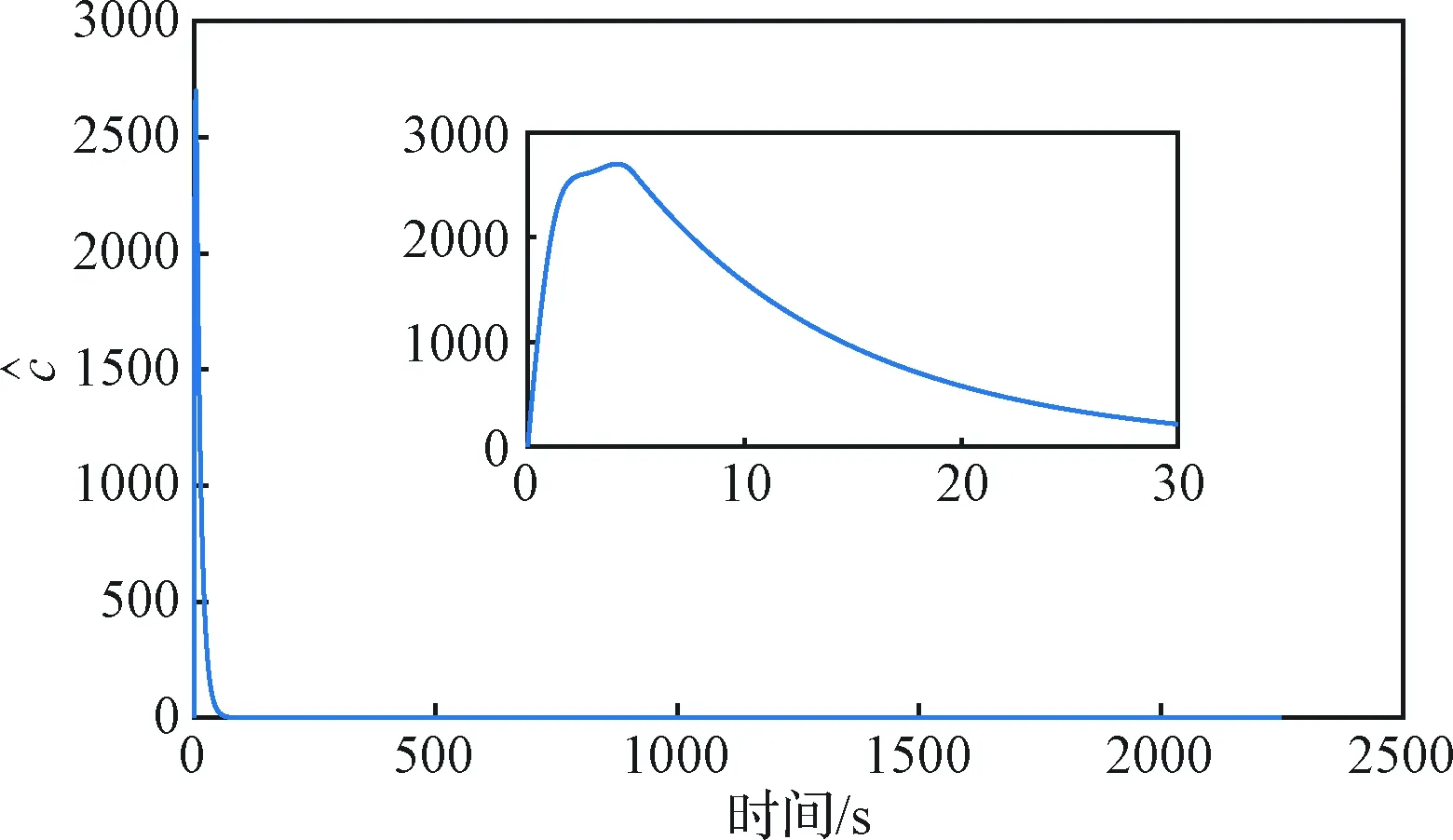
图8 自适应参数Fig.8 Estimated parameter
4 结 论
由于再入飞行过程的复杂性以及环境的恶劣,使得飞行器的执行机构也容易发生故障。本文研究了姿态环中执行机构发生故障时的姿态容错控制。本文设计的姿态容错控制系统分两步设计,首先针对运动学设计期望的角速度,作为虚拟控制量,保证运动学能跟踪上期望的气动角,然后再根据动力学方程,设计控制力矩跟踪期望角速度。仿真表明,在存在外界干扰和不需要转动惯量信息的情况下,该控制律对于所提加性故障和乘性故障并不敏感,具有较快的收敛速度和较强的抗干扰能力。
参 考 文 献
[1] 王大轶, 郭敏文. 航天器大气进入过程制导方法综述[J]. 宇航学报, 2015, 36(1):1-8. [Wang Da-yi, Guo Min-wen. Review of spacecraft entry guidance[J]. Journal of Astronautics, 2015, 36(1):1-8.]
[2] 龚宇莲, 吴宏鑫. 基于特征模型的高超声速飞行器的自适应姿态控制[J]. 宇航学报, 2010, 31(9): 2122-2128. [Gong Yu-lian, Wu Hong-xin. Characteristic model-based adaptive attitude control for hypersonic vehicle [J]. Journal of Astron-autics, 2010, 31(9): 2122-2128.]
[3] Shtessel Y, McDuffie J, Jackson M, et al. Sliding mode control of the X-33 vehicle in launch and re-entry modes[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Reston, USA, 1998.
[4] Shtessel Y, Hall C, Jackson M. Reusable launch vehicle control in multiple-time-scale sliding modes [J]. Journal of Guidance Control and Dynamics, 2000, 23(6): 1013-1020.
[5] 耿洁, 刘向东 ,盛永智, 等. 飞行器再入段最优自适应积分滑模姿态控制[J]. 宇航学报, 2013, 34(9): 1215-1223. [Geng Jie, Liu Xiang-dong, Sheng Yong-zhi, et al. Optimal ada-ptive integral sliding mode control for reentry vehicle attitude [J]. Journal of Astronautics, 2013, 34(9):1215-1223.]
[6] Da Costa R R, Chu Q P, Mulder J A. Reentry flight controller design using nonlinear dynamic inversion [J]. Journal of Spacecraft and Rockets, 2003, 40(1): 64-71.
[7] Juliana S, Chu Q P, Mulder J A, et al. Flight control of atmospheric re-entry vehicle with non-linear dynamic inversion [C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, USA, August 16-19, 2004.
[8] Well K H, Wallner E M. Nonlinear flight control design for the X-38 using CMAC neural networks[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, Canada, August 6-9, 2001.
[9] Recasens J J, Chu Q P, Mulder J A. Robust model predictive control of a feedback linearized system for a lifting-body re-entry vehicle[C]. AIAA Guidance, Navigation, and Control Confe-rence and Exhibit, San Francisco, USA, August 15-18, 2005.
[10] 王玉惠, 吴庆宪, 姜长生, 等. 基于模糊前馈的空天飞行器再入姿态的模糊鲁棒跟踪控制[J]. 宇航学报, 2008, 29(1):150-155. [Wang Yu-hui,Wu Qing-xian, Jiang Chang-sheng, et al. Fuzzy robust tracking control for aerospace vehicle’s reentry attitude based on fuzzy feedforward[J]. Journal of Astronautics, 2008, 29(1):150-155.]
[11] 程路, 姜长生, 都延丽, 等. 基于滑模干扰观测器的近空间飞行器非线性广义预测控制[J]. 宇航学报, 2010, 31(2):423-431. [Cheng Lu, Jiang Chang-sheng, Du Yan-li, et al. The research of SMDO based NGPC method for NSV control system [J]. Journal of Astronautics, 2010, 31(2):423-431.]
[12] Shen Q, Jiang B, Cocquempot V. Fault diagnosis and estimation for near-space hypersonic vehicle with sensor faults [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2012, 226(3): 302-313.
[13] Qi R, Tao G, Jiang B, et al. Adaptive control schemes for discrete-time T-S fuzzy systems with unknown parameters and actuator failures [J]. IEEE Transactions on Fuzzy Systems, 2012, 20(3): 471-486.
[14] 林常青, 宗群. 临近空间飞行器的模型参考滑模容错控制[J]. 控制工程, 2012, 19(1): 119-122. [Lin Chang-qing, Zong Qun. Model reference sliding mode fault-tolerant control for near space vehicles [J]. Control Engineering of China, 2012, 19(1): 119-122.]
[15] Zhao J, Jiang B, Shi P, et al. Fault-tolerant control design for near-space vehicles based on a dynamic terminal sliding mode technique [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2012, 226(6): 787-794.
[16] Fiorentini L, Serrani A, Bolender M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-416.
[17] Jiang Y, Hu Q, Ma G. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures [J]. ISA Transactions, 2010, 49(1): 57-69.
