间接Legendre伪谱法的欠驱动航天器姿态运动轨迹跟踪
2018-07-03易中贵戈新生
易中贵,戈新生
(1. 北京理工大学宇航学院,北京 100081;2. 北京信息科技大学机电工程学院,北京 100192)
0 引 言
近年来,随着航天科学技术快速发展,特别是空间交会对接以及深空探测技术的发展使得航天器系统的规模越来越大,自由度越来越多,构造与功能日益复杂,技术要求逐渐提高,所涉及的领域不断扩大,需要考虑的因素急剧上升,对运行的速度以及精度也提出了更高的要求。从而增加了姿态动力学建模、控制仿真分析及运行维护的难度。因此航天器动力学与控制学科的研究受到了越来越多科研工作者的青睐。航天器姿态控制系统是多个不同功能分系统里面的一个重要分系统。航天器对其姿态的指向精度有着非常严格的要求,如为确保航天器对地通信信号质量而使所携带的通信天线的方向应长时间精确指向地球方向、航天器展开的太阳帆板需指向太阳方向、空间站等的交会对接过程以及空间机械臂在轨执行任务等等。正常情况下,安装有足够或冗余执行机构(如n个飞轮/控制力矩陀螺,或者n对喷气推力器(n≥ 3))的三轴稳定航天器姿态控制系统可以在滚转、俯仰和偏航三轴同时输出控制力矩,完成其姿态控制和任意定位。但航天器系统的姿态控制任务繁多、系统结构复杂,执行机构长期处于真空、失重、超低温以及强辐射等实际的恶劣环境中执行在轨任务容易导致其中的某一个发生故障或者失效,从而不能输出完整的三轴控制力矩,故称此时的航天器系统为欠驱动航天器。欠驱动航天器姿态动力学与控制的研究最早可追溯到20世纪80年代,1984年,Crouch[1]基于微分几何理论研究了刚体航天器所安装的执行机构(喷气推力器或动量飞轮)数目少于3个时的可控性问题,并设计了相应的控制算法,其研究表明,在系统的动量矩不等于零时,欠驱动航天器并不可控。Krishnan等[2]根据局部可控性定理研究得到:欠驱动航天器系统能控的充要条件是其欠驱动轴不能是其对称轴。之后国内也有不少学者对其进行了更深入的研究和探讨,如文献[3-4]通过动量矩守恒定理先建立了以两个动量飞轮为执行机构的欠驱动航天器的姿态动力学方程,并在整星零动量的条件下,分别采用Ritz 近似理论以及粒子群优化方法,研究了带两个反作用动量飞轮的欠驱动航天器系统的姿态非完整机动规划问题。王芳等[5]研究了航天器上的挠性件以及大气阻力带来的正弦干扰力矩情况下的姿态控制问题中的旋转轴稳定问题。郑敏婕等[6]采用退步控制设计方法研究了欠驱动航天器系统的姿态控制率设计问题。近年来,张洪华等[7]研究了欠驱动挠性航天器的姿态控制问题,提出了“喷气消旋+飞轮机动”的分段控制方法,并针对此方法的完整过程,采用了扰动系统理论分析闭环控制系统的大范围终端有界性。张佳为等[8]针对欠驱动刚体航天器姿态控制问题,采用非线性预测控制方法实现了任意飞轮群剪刀对构型、飞轮群角动量非饱和条件下,任意系统初始角动量欠驱动航天器在姿态可机动集合中的机动控制。宋道喆等[9]通过Lyapunov直接法和Backstepping方法设计一种非线性不连续反馈控制律来研究了轮控式零角动量欠驱动航天器的姿态最优稳定控制问题。
对于欠驱动航天器的姿态机动控制问题, Legendre伪谱法(Legendre pseudospectral method,LPM)具有较高的精度和较快的运算速度,它通过一系列数值近似变换,将一个连续的最优控制问题离散为一个非线性规划(Non-linear programming,NLP)问题来求解。LPM最初由Elnagar等[10]提出,之后Roa等[11]在此基础上对其进行分析、扩展,并应用到更广范的问题上。且Fahroo等[12]的研究提出, 对于一个末端是非完全自由的最优控制问题,特别是当末端约束是含初始或终端状态的表达式时,Gauss和Radau伪谱法可能不收敛,然而Legendre伪谱法此时却具有较好的收敛精度和效果。在国内,Zhuang等[13]先采用系统的微分平滑特性转化欠驱动航天器的状态和控制输入变量为一平滑输出函数,然后采用LPM离散此平滑函数为一NLP问题,进而求解出系统的最短时间姿态机动轨迹。
针对欠驱动航天器的姿态运动跟踪问题,目前出现的研究成果多采用航天器系统的微分平滑特性以及间接LPM对其姿态运动和跟踪问题进行研究和探讨[14-18]。Aguilar[14]通过证明欠驱动航天器系统在特殊的转动惯量值时是微分平滑的,然后根据平滑特性规划出系统的开环参考轨迹,最后再根据动态扩展算法设计跟踪控制器,从而将线性化系统的姿态稳定到系统的平衡点附近。Tsiotras[15]则先采用系统的微分平滑特性规划出系统的可行轨迹,再将其用于后续的轨迹跟踪问题中去。文献[16]基于LPM先规划出欠驱动航天器的最短时间姿态机动参考轨迹。接着考虑到系统在执行任务过程中不可避免会有初值扰动和不利的干扰激励等外界因素,进而分别采用间接LPM和系统扩展后的特殊几何特性设计了系统的闭环轨迹跟踪控制器。文献[17]则基于改进的Chebyshev伪谱法,采用系统的微分平滑特性以及滚动时域控制方法研究了欠驱动航天器的姿态运动轨迹跟踪控制问题。文献[18]采用间接LPM研究了高超声速飞行器再入滑翔的纵向参考轨迹跟踪制导问题。廖宇新等[19]采用间接Radau伪谱法研究了高超声速飞行器滑翔段的制导问题,先将标称轨迹跟踪问题转化为线性时变系统的状态调节器问题,然后基于Pontryagin极大值原理将状态调节器问题转化为线性两点边值问题(Two-point boundary value problem,TPBVP);最后采用间接Radau伪谱法离散所求得的两点边值问题为一组线性方程组,避免了在线积分求解Riccati矩阵微分方程等复杂的数值计算,数值仿真结果验证了所提方法具有良好的鲁棒性。
本文研究了欠驱动航天器存在有较小初始外部扰动时的最短时间姿态机动优化和跟踪问题。首先采用LPM离线规划出系统的最短时间姿态机动参考轨迹。接着根据最优性原理将跟踪问题转化为一个两点边值问题。鉴于LPM在求解末端约束含有初始或终端状态表达式时比Radau伪谱法具有较好的收敛精度[12]。且LPM还具备方阵形式的微分矩阵(离散的线性方程组的个数等于变量个数)[16]。因此本文基于LPM离散微分方程的思路(并将此方法称之为间接Legendre伪谱法),采用Legendre-Gauss-Lobatto (LGL)点离散转化TPBVP为一组线性方程,避免了对传统Riccati微分方程的积分运算。文末给出了数值仿真运行结果。
1 运动模型
根据欧拉定理可知:空间参考坐标系转动三次即可到达航天器的本体坐标系。本文选取3-2-1的旋转顺序。以欧拉角作为姿态描述参数的航天器姿态运动学方程[16]
(1)
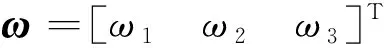
假设航天器系统没有外力矩作用,且惯量主轴的方向与本体坐标系的方向是同向的,则可写出航天器的姿态动力学方程[16]
(2)
(3)
(4)
式中:α=(I1-I2)/I3称为系统的轴不对称性系数。
2 姿态机动控制
本文先离线规划出系统的最短时间姿态机动轨迹,并将此优化轨迹作为后续姿态运动轨迹跟踪的参考轨迹。文中的最短时间控制问题可描述为
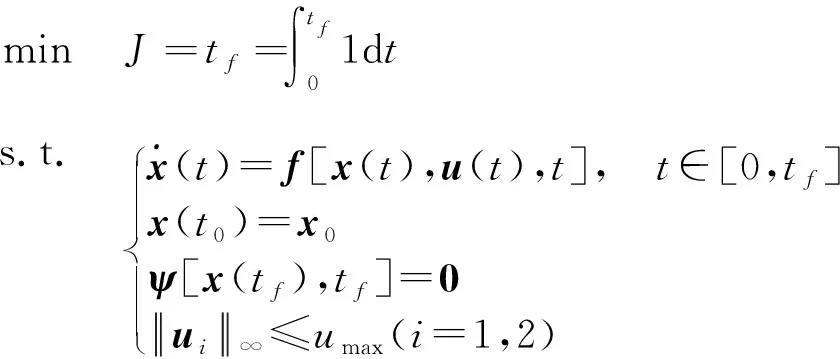
minJ=tf=∫tf01dts.tx(t)=f[x(t),u(t),t], t∈[0,tf]x(t0)=x0ψ[x(tf),tf]=0ui∞≤umax(i=1,2)
(5)
其中,ψ[·]表示终端约束条件,umax代表控制输入力矩的上限值。接着采用Legendre伪谱法离散逼近式(5)所描述的最优控制问题,将其转化为一个非线性规划问题来求解。鉴于此部分内容国内外已有较多相关文献[10-11],这里不再赘述。
通过LPM将一个连续最优控制问题转化成的NLP问题可通过SQP算法求解便可得到原时间最优控制问题的近似解。文中采用SNOPT软件包对此NLP问题进行求解。
3 姿态运动跟踪
3.1 两点边值问题的描述
将欠驱动航天器系统的动力学方程(式(4))在
已知的参考姿态运动轨迹上进行泰勒展开,并略去高阶项仅保留一次项,从而有线性化方程
(6)
式中:Δx(t)=[Δω1,Δω2,Δω3,Δφ,Δθ,Δψ]T为状态变量实际值x与参考值x*的偏差,而Δu(t)=[Δu1,Δu2]T为输入控制变量u的修正量,Δx0为状态初始扰动。时变状态矩阵A(t)∈R6×6的表达式为
(7)
时变控制输入矩阵B(t)∈R6×2的表达式为
(8)
姿态运动的跟踪问题可描述为:通过确定控制输入修正量Δu(t)以及状态偏差量Δx(t),使得如下二次型性能指标最小
ΔuT(t)RΔu(t)]dt
(9)
并满足线性系统的误差状态方程以及初始条件(式(6))。式中S∈R6×6为半正定的末端加权矩阵,Q∈R6×6为半正定的状态加权阵,R∈R2×2是正定的控制加权阵。根据Pontryagin极小值原理[20],引入协态变量λ(t)∈R6,并构造Hamilton函数,则最优状态Δx*(t)和最优协态λ*(t)满足正则方程
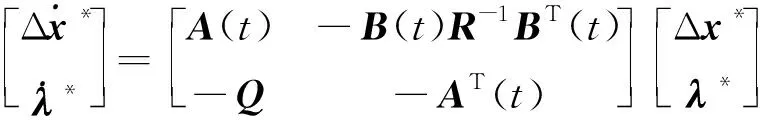
(10)
边界条件与最优协态λ*(t)满足的横截条件为
(11)
且根据Hamilton函数取极小值时的必要条件有最优控制修正量满足
Δu*(t)=-R-1λ*T(t)B(t)=-R-1BT(t)λ*(t)
(12)
3.2 两点边值问题的离散
借鉴LPM离散微分方程的思路。首先通过变换t=(1+τ)tf/2把时间区间t∈[0,tf]转换到区间τ∈[-1,1]上。进而由式(10)和式(11)所描述的两点边值问题可转化为
(13)
选取K+1个LGL离散配点,将状态变量和协态变量在这些配点上进行Lagrange插值,并求导有
(14)
将式(14)代入式(13)可得两点边值问题的离散表达式为
(15)
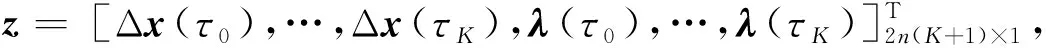
Xz=Y
(16)
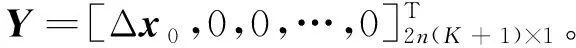
(17)
(18)
(19)
(20)
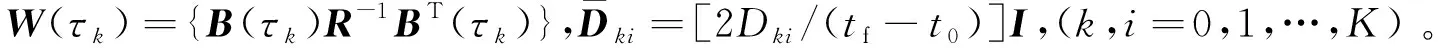
至此,整个算法在执行过程中不需要任何的积分运算,只需计算线性方程组(16)的解便可求得两点边值问题(式(10)~(11))的离散解。此算法既能保证计算精度,又能有效减小计算量和运算时间。
4 数值仿真
本文先采用LPM离线优化出欠驱动航天器的最短时间姿态机动轨迹。假设欠驱动航天器进行rest-to-rest的姿态机动控制,其惯量主轴[14]设为I=diag(66.36,61.80,50.16) kg·m2;初末姿态约束[14]分别设置为x0=[0,0,0,-π/2,-π/3,π/2]T,xf=[0,0,0,π/2,π/3,-π/2]T;执行机构控制输入上限为umax=1(根据Pontryagin极小值原理[16,20],输入力矩应具有Bang-Bang控制的形式,且在上下限之间切换);离散点个数设置为LGL=37; NLP的求解器为SNOPT[21],且其求解初值设为ones(8×38+1,1)。
针对欠驱动航天器存在初始小扰动进行姿态跟踪。先设置初始偏差值Δx0(见表1)[17],选择与参考轨迹相同的LGL配点个数,代入线性方程组(16)便可得到最优协态λ*(t),将其代入方程(12)求得最优控制修正量Δu*,进而可得到实际的控制输入u=u*+Δu*(u*为参考轨迹中规划而得的最优控制量)。将此控制输入代入系统运动模型(式(4))进行积分便可求得其实际的姿态运行轨迹x。状态偏差可由Δx=x-x*得到。加权矩阵S,Q和R可根据Bryson’s Rule确定[22]
(21)
式中:下标max表示各变量所允许的最大偏差,本文取状态变量的最大偏差为2Δx0,而控制变量的最大偏差取为[0.0055, 0.0055]。并设Q11=1,则矩阵Q和R中的其余元素便可由式(21)确定。
具体仿真结果见图1~图5,图中同时给出了姿态机动参考轨迹以及两种极限初始小扰动情况下的闭环和开环跟踪控制曲线。

表1 初始扰动Table 1 The initial disturbance
注:表1中Δω的单位为rad/s,三个欧拉角的单位为度。
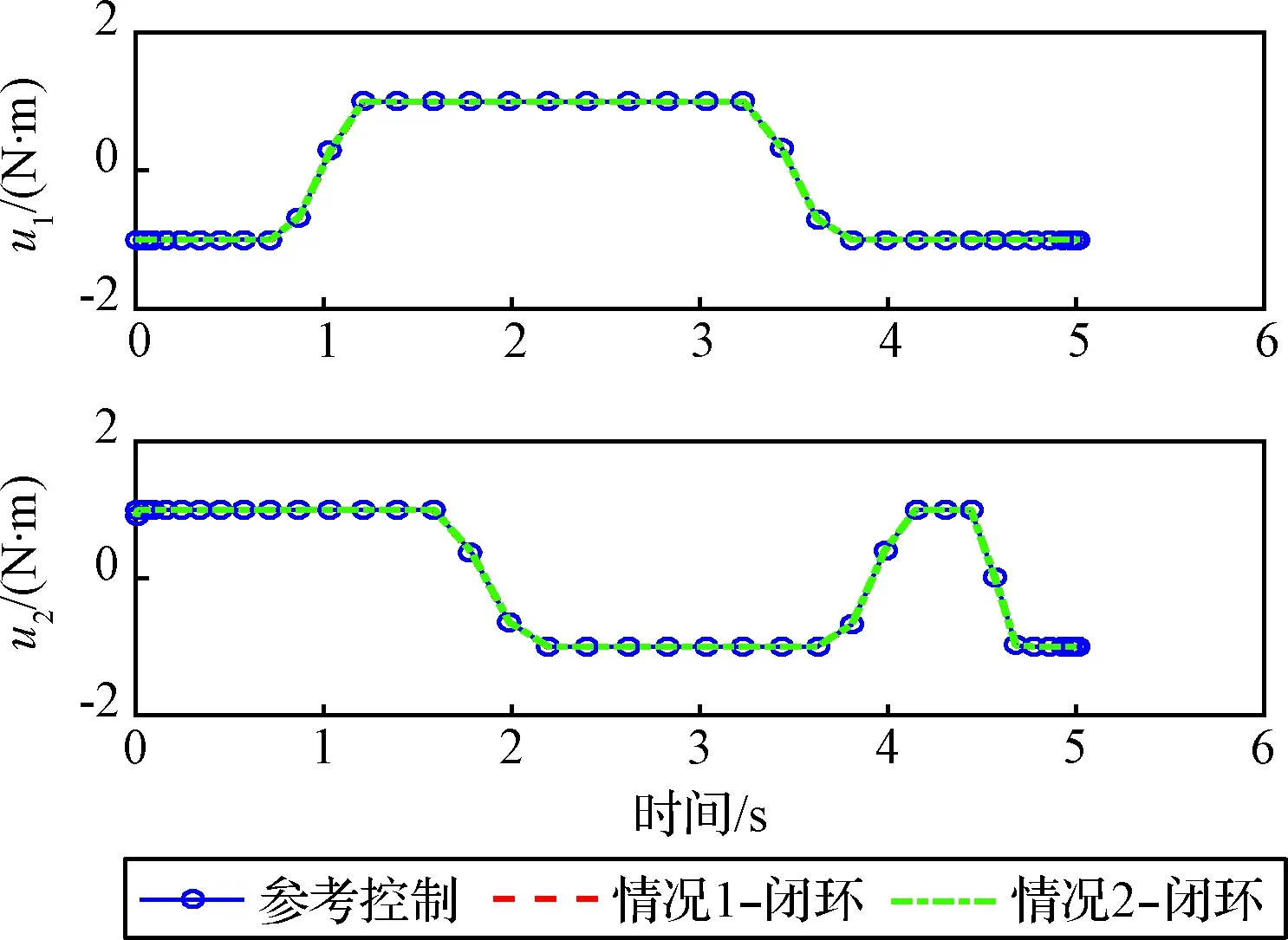
图1 参考及跟踪控制输入Fig.1 The reference and tracking control torques
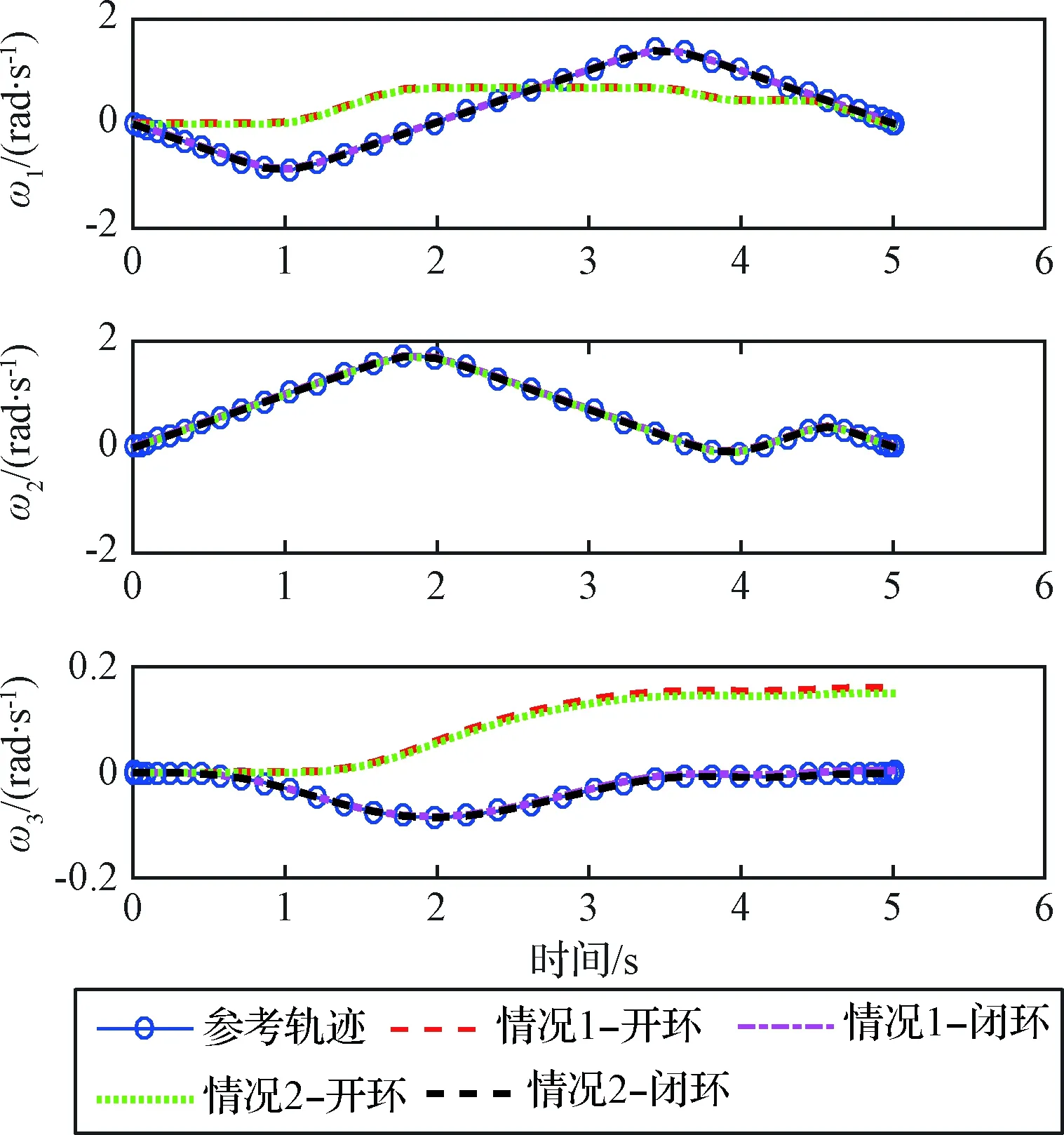
图2 角速度的参考、开环以及闭环轨迹Fig.2 The trajectories for angular velocities
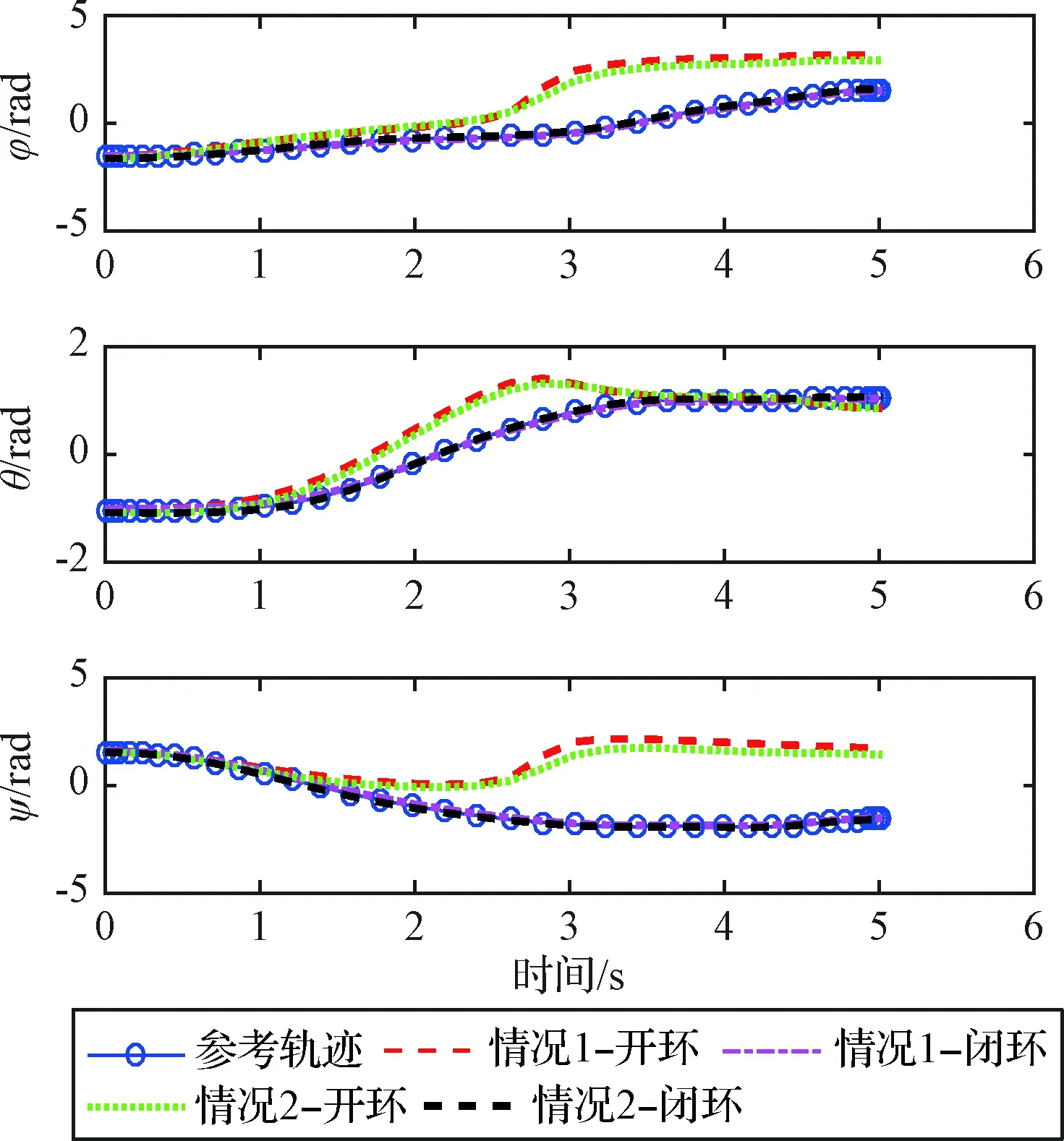
图3 姿态角的参考、开环以及闭环轨迹Fig.3 The trajectories for Euler angles
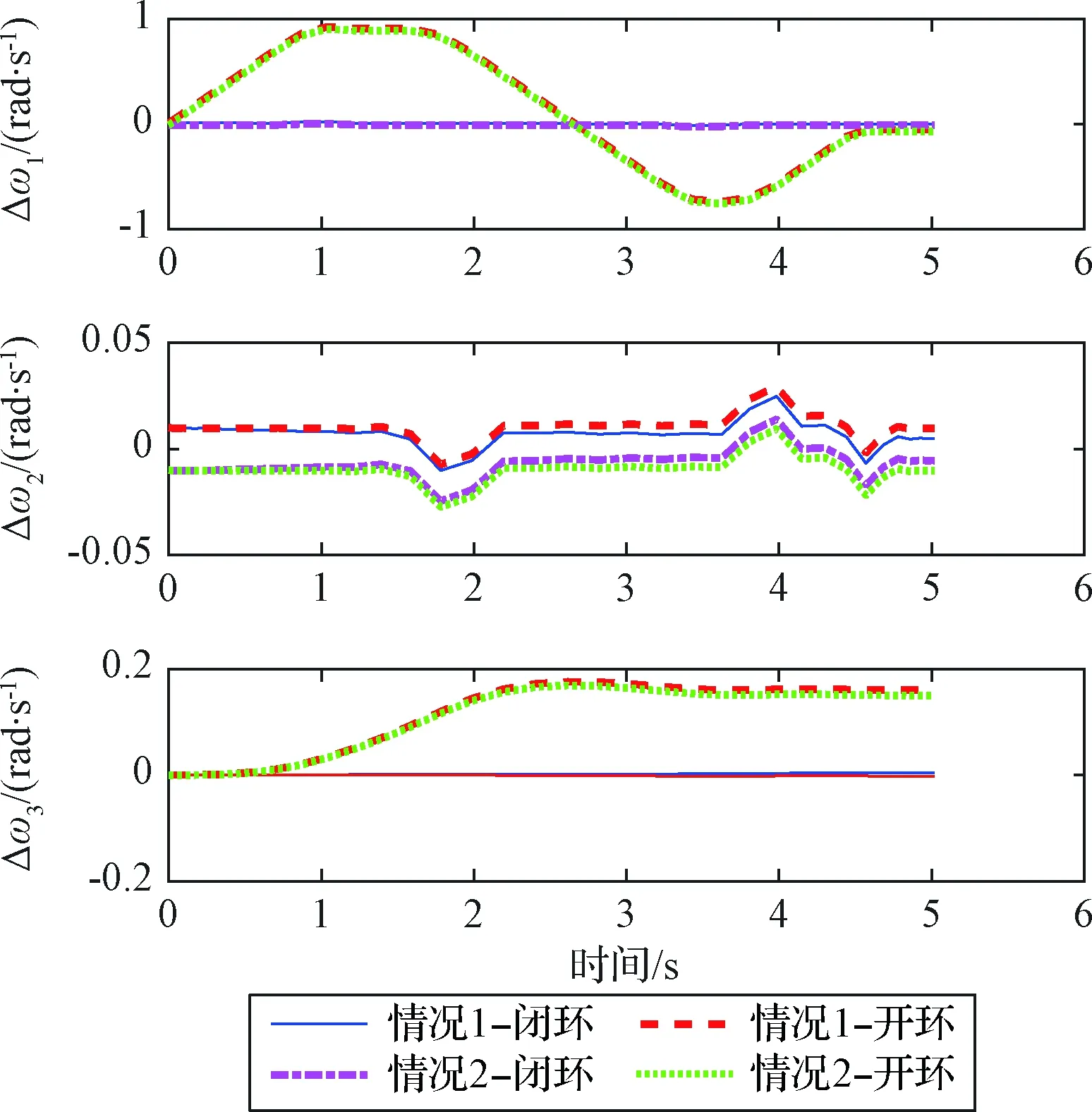
图4 角速度跟踪误差曲线Fig.4 The tracking errors for angular velocities
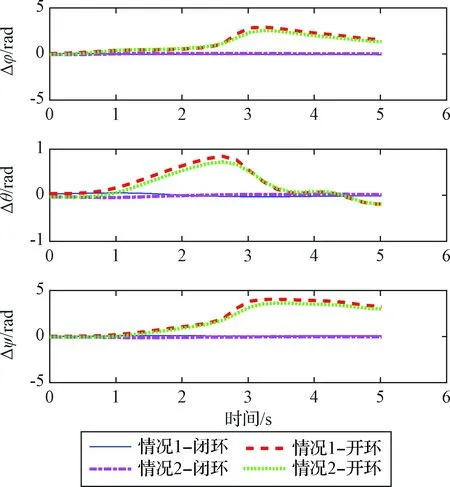
图5 姿态角跟踪误差曲线Fig.5 The tracking errors for Euler angles
从图1中的控制输入满足开关控制(Bang-Bang控制)的形式,且在预设的最大和最小控制值之间切换。从图2~3中的参考轨迹可以看出,三个欧拉姿态角和姿态角速度均可精确规划到预定的末端值,优化曲线均平滑,优化目标的最短时间为5.0166 s。
图2~3中的点划线和虚线分别代表上下极限初始扰动情况下的闭环跟踪控制曲线,而细实线和点线则分别为带有上下极限初始小扰动的开环跟踪控制曲线。从图2~3可以看出,闭环跟踪效果较好,对初始外部扰动具有一定的抑制能力,而开环则不能跟踪到目标点,这可从图4~5中的跟踪误差曲线得到体现。
5 结 论
本文研究了带有两组喷气推力器的非对称欠驱动航天器的姿态优化控制及其姿态运动跟踪问题。先采用LPM规划出欠驱动航天器的最短时间姿态机动参考轨迹。接着采用LGL点离散时变偏差系统的TPBVP,将其转化为一组线性方程组来求解,避免了对Riccati方程的积分运算。最后通过数值仿真校验了本文所提出算法的有效性和合理性。
参 考 文 献
[1] Crouch P E. Spacecraft attitude control and stabilization: applic-ation of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control, 1984, 29(4): 87-95.
[2] Krishnan H, Mc clamroch N H, Reyhanoglu M. Attitude stabilization of a rigid spacecraft using two momentum wheel actuators[J]. Journal of Guidance Control & Dynamics, 1995, 18(2): 256-263.
[3] 戈新生, 陈立群, 刘延柱. 带有两个动量飞轮刚体航天器的姿态非完整运动规划问题[J]. 控制理论与应用, 2004, 21(5): 781-784. [Ge Xin-sheng, Chen Li-qun, Liu Yan-zhu. Nonholonomic motion planning for the attitude of rigid spacecraft with two momentum wheel actuators[J]. Control Theory & Applications, 2004, 21(5): 781-784.]
[4] 戈新生, 孙鹏伟. 欠驱动刚性航天器姿态的非完整运动规划粒子群算法[J]. 宇航学报, 2006, 27(6): 1233-1237. [Ge Xin-sheng, Sun Peng-wei. Nonholonomic motion planning for the attitude of underactuated spacecraft using particle swarm optimization[J]. Journal of Astronautics, 2006, 27(6): 1233-1237.]
[5] 王芳, 张洪华. 欠驱动刚性航天器旋转轴稳定研究[J]. 宇航学报, 2007, 28(5):1133-1137. [Wang Fang, Zhang Hong-hua. Spin-axis stabilization of underactuated rigid spacecraft[J]. Journal of Astronautics, 2007, 28(5):1133-1137.]
[6] 郑敏捷, 徐世杰. 欠驱动航天器姿态控制系统的退步控制设计方法[J]. 宇航学报, 2006, 27(5):63-66. [Zheng Min-jie, Xu Shi-jie. Backstepping control for attitude control system of an underactuated spacecraft[J]. Journal of Astronautics, 2006, 27(5):63-66.]
[7] 张洪华, 王芳, 胡锦昌, 等. 欠驱动挠性航天器的全姿态控制[J]. 宇航学报, 2015, 36(4):419-429. [Zhang Hong-hua, Wang Fang, Hu Jin-chang, et al. All-attitude control for underactuated flexible spacecraft[J]. Journal of Astronautics, 2015, 36(4):419-429.]
[8] 张佳为, 许诺, 伍少雄. 欠驱动航天器飞轮控制方法[J]. 宇航学报, 2016, 37(5):552-561. [Zhang Jia-wei, Xu Nuo, Wu Shao-xiong. Control method of underactuated spacecraft using flywheels[J]. Journal of Astronautics, 2016, 37(5):552-561.]
[9] 宋道喆, 耿云海, 易涛. 零角动量欠驱动航天器逆最优稳定控制律设计[J]. 宇航学报, 2016, 37(6):729-736. [Song Dao-zhe, Geng Yun-hai, Yi Tao. Inverse optimal stabilization of an underactuated spacecraft in a zero angular momentum mode[J]. Journal of Astronautics, 2016, 37(6):729-736.]
[10] Elnagar G N, Kazemi M A. The pseudospectral Legendre method for discretizing optimal control problems[J]. IEEE Transactions on Automatic Control, 1995, 40(10):1793-1796.
[11] Rao A V, Clarke K A. Performance optimization of a maneuvering reentry vehicle using a Legendre pseudospectral method[J]. AIAA Journal, 2002.
[12] Fahroo F, Ross I M. Advances in pseudospectral methods for optimal control[C]. AIAA Guidance, Navigation and Control Conf and Exhibit, Honolulu,USA, 2008.
[13] Zhuang Y F, Guang-Fu M A, Chuan-Jiang L I, et al. Time-optimal trajectory planning for underactuated rigid spacecraft using differential flatness[J]. Journal of Astronautics, 2011, 32(8):1753-1761.
[14] Aguilar C O. Attitude control of a differentially flat underactuated rigid spacecraft [D]. Edmonton: University of Alberta, 2005.
[15] Tsiotras P. Feasible trajectory generation for underactuated spacecraft using differential flatness[J]. Advances in the Astronautical Sciences, 2008, 103:16-18.
[16] 庄宇飞. 带有非完整约束的欠驱动航天器控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. [Zhuang Yu-fei. Control of underactuated spacecraft with nonholonomic constraints[D]. Harbin: Harbin Institute of Technology, 2012.]
[17] Cai W W, Yang L P, Zhu Y W. Optimal reorientation of asymmetric underactuated spacecraft using differential flatness and receding horizon control[J]. Advances in Space Research, 2015, 55(1):343-353.
[18] 李强. 高超声速滑翔飞行器再入制导控制技术研究[D]. 北京: 北京理工大学, 2015. [Li Qiang. Study on reentry guidance and control method for hypersonic glide vehicle[D]. Beijing: Beijing Institute of Technology, 2012.]
[19] 廖宇新, 李惠峰, 包为民. 基于间接Radau伪谱法的滑翔段轨迹跟踪制导律[J]. 宇航学报, 2015, 36(12):1398-1405. [Liao Yu-xin, Li Hui-feng, Bao Wei-min. Gliding trajectory tracking guidance law based on indirect Radau pseud-ospectral method[J]. Journal of Astronautics, 2015, 36(12):1398-1405.]
[20] 李传江,马广富. 最优控制[M]. 北京: 科学出版社, 2011.
[21] Gill P E, Murray W, Saunders M A. SNOPT: an SQP algorithm for large-scale constrained optimization[J]. Siam Journal on Optimization, 2002, 12(1):99-131.
[22] Bryson D E, Ho Y C. Applied optimal control[M]. Washington, D C: Hemisphere Publishing Corporation, 1975.
