一种求解轨迹优化问题的改进多分辨率技术
2018-07-03赵吉松
赵吉松,李 爽
(南京航空航天大学航天学院,南京 210016)
0 引 言
轨迹优化对于飞行器设计有着重要意义和工程实际价值。轨迹优化属于最优控制问题,其求解方法主要分为间接法和直接法[1]。间接法借助变分法或庞特里亚金最大值原理,把泛函优化转化为边值问题求解;直接法通过对控制变量和/或状态变量进行离散把泛函优化转化为非线性规划(Nonlinear programming,NLP)求解。直接法中的配点法由于不需要推导最优性必要条件,并且对初值的敏感性较低,容易收敛,近年来得到广泛研究。
如果需要高精度求解轨迹优化问题,均匀加密不是一种较好的方案。因为这样处理会导致计算量显著增加,需要更多的计算资源,并且随着节点数目的增加,算法的收敛性通常变差。这种情况下有必要引入网格细化技术对离散节点进行局部加密或者调整,在轨迹变化平缓区域采用稀疏网格,在轨迹变化剧烈的区域采用稠密网格。目前国内外研究者在网格细化方面已做了不少工作。对于局部配点法[2],由于离散格式本身对于节点分布没有限制,因而局部配点法的离散节点可以根据需要任意布置。用于局部配点法的节点细化方法有离散误差分析[3]、小波分析[4-5]、多分辨率技术(Multiresolution techniques, MRT)[6-9]、密度函数法[10]等。对于全局配点法(又称伪光谱法)[11],其离散节点是正交多项式的根,分布特点是中间稀两端密,但是一旦节点数目给定,节点的分布情况也随之确定。因此,全局配点法的离散节点不可随意布置,其网格细化没有局部配点法灵活。全局配点法的网格细化方法通常是通过添加结点(段与段之间的连接点称为结点)将问题分段优化,利用结点附近的离散节点较密的特点达到加密网格的效果,比如结点伪谱法[12],hp自适应伪谱法[13],ph伪谱法[14],以及最新提出的既能添加又能减少离散节点的自适应网格细化算法[15]。分段优化面临的主要问题是在解出最优控制问题之前通常很难知道需要分多少段以及在哪分段,若通过优化确定这些信息往往会存在分段过多、采用的离散节点较多等弊端[13-15]。
在各种网格细化算法中,多分辨率技术[6-7]比较有吸引力。该技术分析各个节点处的插值误差,如果某个节点处的插值误差较大,则在该节点附近进行细化网格,否则不进行细化。多分辨率技术具有原理简单、使用灵活、鲁棒性好、采用的离散节点较少等多方面优势。但是,文献[6-7]给出的多分辨率技术没有对初始网格中的偶数节点进行细化,由此可能会导致细化遗漏,并且在细化过程中由于非光滑区域的移动可能会发生无法继续细化的情况,即细化失败。此外,文献[6-7]给出的多分辨率技术基于二进网格,其初始网格节点数目必须是2j+1(j为非负整数),使用不方便。文献[9,16]将其推广至广义二分网格,克服了这一限制,但是优化采用的初始网格的节点数目必须是基础网格的二倍,这种不一致给使用带来不便。文献[16]通过引入节点检测算法避免了细化遗漏或失败问题,但是该网格细化方法需要的迭代次数较多,细化效率不高。
针对多分辨率技术的不足之处,本文提出一种改进多分辨率方法,既能够避免多分辨率技术的细化遗漏问题,又具有较高的细化效率,并且初始网格节点数可以取任意奇数而不限于2j+1。
1 最优控制问题数学描述
以Bolza型最优控制问题为例,可描述为:求解控制变量u(t)∈Rm,使得如下目标函数最小化

(1)
式中:端点项M:Rm×R×Rn×Rm→R, 积分项L:Rn×Rm×R→R,x∈Rn,t∈[t0,tf]⊆R。
状态方程为
(2)
端点(边界)条件为
E(x(t0),t0,x(tf),tf)=0
(3)
路径约束为
C(x(t),u(t),t)≤0,t∈[t0,tf]
(4)
式中:f:Rn×Rm×R→Rn,E:Rn×R×Rm×R→Re,C:Rn×Rm×R→Rc。方程(1)~(4)描述的问题称为Bolza型最优控制问题。
2 基于Runge-Kutta格式的配点法离散
2.1 广义二分网格
传统二进网格的初始节点数目必须是2j+1(j为非负整数),使用不方便。文献[9,16]给出了一种广义二分网格,但是用于优化的初始网格节点数目必须是基础网格的二倍,使用仍然不够灵活。为此,本文重新定义一种广义二分网格。
在区间[0, 1]内,由N个均匀分布的初始子区间对分得到的二分网格为
Vj,N={τj,k∈[0,1]:τj,k=k/(2jN),
0≤k≤2jN}, -1≤j≤Jmax
(5)
式中:整数j表示网格分辨率,整数k表示节点位置,整数Jmax表示最高分辨率。由于j的最小值为-1,因而N必须为偶数。采用Wj, N表示属于Vj+1, N但不属于Vj, N的网格节点,即
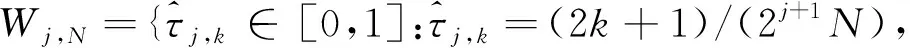
(6)
因此,τj+1, k∈Vj+1, N满足如下关系
(7)
二分网格的子空间Vj, N满足嵌套关系,即V0, N⊂V1, N⊂…⊂VJmax, N,并且当Jmax→∞时,VJmax, N=[0, 1]。子空间Wj, N满足Wj, N∩Wl, N=∅(j≠l)。由定义(5)和(7)可知,二分网格是将区间[0, 1]不断细分获得,并且当k≥j时满足Wk, N∩Vj, N=∅。
图 1给出一组广义二分网格的示例(N=6,Jmax=5)。其中V0, N=V-1, N∪W-1, N通常作为初始网格。对于实际问题,N可根据需要取任意偶数。
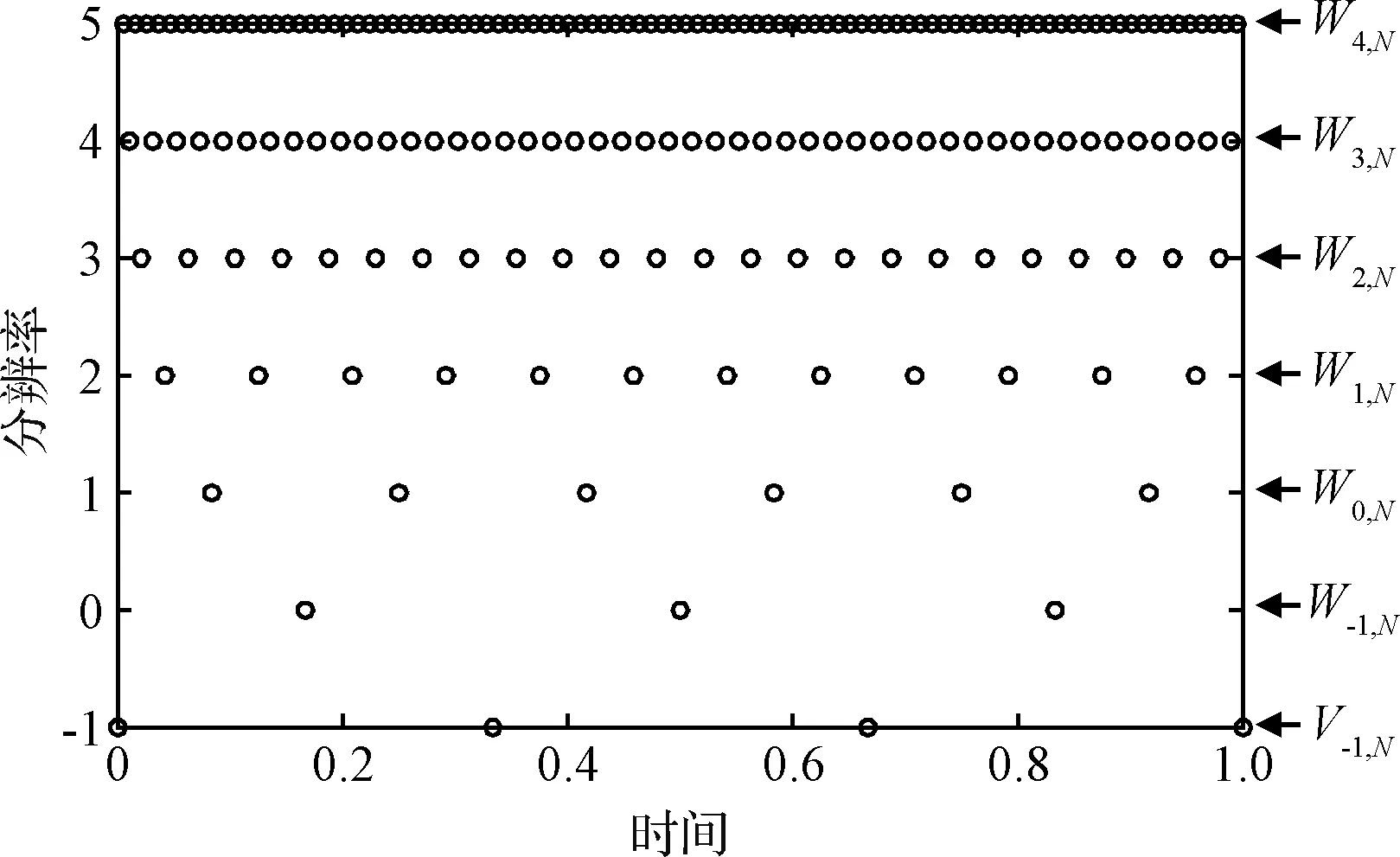
图1 广义二分网格的示例(N = 6, Jmax= 5)Fig.1 Generalized dyadic mesh with N = 6 and Jmax= 5
2.2 Runge-Kutta离散格式
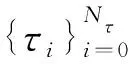
(8)
并且满足如下约束
(9)
Ci=C(xi,ui,τi;t0,tf)≤0
(10)
(11)
E(x0,t0,xf,tf)=0
(12)
式中:Δt=tf-t0,hi=τi+1-τi,fij=f(xij,uij,τij;t0,tf),Lij=L(xij,uij,τij;t0,tf),变量xij,uij和τij为区间[τi,τi+1]内的中间变量。xij由下式给出
(13)
式中:τij=τi+hiρj,uij=u(τij)。ρj,βj,αjl均为已知常数并且满足0≤ρ1≤ρ2≤…≤ρq≤1。当αjl=0(l≤j)时,离散格式为显式格式,否则为隐式格式。
变量q为离散格式的阶数。常用的格式包括梯形格式(q= 2),Hermite-Simpson格式(q= 3),以及经典四阶Runge-Kutta格式(q= 4)。
3 改进多分辨率技术
多分辨率技术的核心思想是根据插值误差对网格进行细化。对于一组离散最优解,该算法在每个节点处通过其周围节点插值计算该节点的函数值。如果插值结果与离散最优解差别较大,则在该节点附近细化网格,否则不进行细化。原始多分辨率技术[6-7]没有对初始网格的偶数节点进行细化,可能存在细化遗漏,并且在细化过程中可能发生不能继续细化的情况。文献[16]对多分辨率技术进行改进,避免了细化遗漏问题,但是细化效率较低。本节给出一种新的改进多分辨率技术,既能避免细化遗漏或者失败问题,又具有较高的细化效率。
在进行多分辨率优化之前,结合轨迹优化问题的精度要求,选取初始节点参数N,网格细化误差ε,最高分辨率Jmax,最大迭代次数Imax(Imax≥Jmax/2)。采用RK方法将轨迹优化问题转化NLP。设置I= 1,Gold=V0, N,估计NLP优化变量初值,将其记为Xold。那么,改进多分辨率方法的流程如下:
1)以Gold为初始网格,Xold为初值求解NLP。
2)网格细化方法如下(步骤(1)~(4)):
令Φold={uj,k:τj,k∈Gold},并将其改写为
Φold={φl(τj,k):l=1,…,m;τj,k∈Gold}。
(1)初始化中间网格Gint=V0, N, 以及相应的函数值Φint={φl(τ0,k)∈Φold, 0≤k≤N;l=1, 2, …,m}, 设j=-1。那么,Gold的细化流程可以分为两步:细化算法和检测算法。
(2)细化算法。
(3)检测算法。
(4)本次细化得到的非均匀网格为Gnew=Gint, 相应的函数值Φnew=Φint。
3)置I′ =I+1。如果细化后网格保持不变,那么结束细化;否则,将步骤1)解出的NLP最优解插值到新网格Gnew,并以此作为新的优化初值Xold, 令Gold=Gnew, 返回步骤1),继续细化。
在上述改进多分辨率技术的各个流程中,细化算法和检测算法是关键,具体算法如下。
细化算法:
1)求Wj, N和Gold的交集
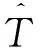
2)设置i=1,执行如下步骤((1)~(6))。
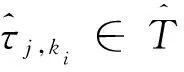
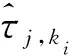
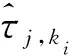
(5)将新增加节点对应的函数值添加到Φint。若新增节点对应的函数值未知,则利用Gold和Φold通过p阶ENO插值计算。
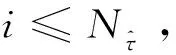
3)将j增加1。若j≤Jmax,返回步骤1),否则转入下一步。
4)结束网格细化算法。
检测算法:
1)设置j为中间网格Gint所包含节点的次高分辨率,即j=min(2I,Jmax)-1。
2)求解Wj, N和Gint的交集
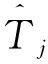
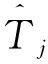
5)根据分辨率层次,将Gcheck分成以下两组:

可见,G1是由Gcheck中的最低分辨率节点组成,G2由其它分辨率节点组成。为了细化Gcheck,首先检查G2中的节点并且进行必要的细化(步骤(1)~(7)),然后采用类似的方法处理G1中的节点。
6)设置i= 1,执行如下步骤((1)~(7))。
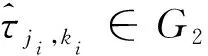
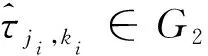
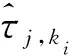
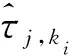
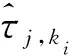
(6)将新增加节点处的函数值添加至Φint,若函数值未知,根据Gold和Φold插值得到。
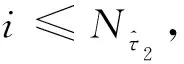
7)采用类似的方法(步骤(1)~(7)),检查G1中的每个节点并进行必要的细化。
4 优化算例
本节应用第3节描述的改进多分辨率技术(简记为IMRT)求解公开文献中的优化算例以验证其有效性,包括Bryson-Denham问题[6-7],小推力轨道转移问题[18],航天器姿态调整问题[19]。对于所有算例,采用Hermite-Simpson离散格式将其转化为NLP,采用SNOPT 7[20]求解NLP,采用INTLAB 5.5[21]提供一阶偏导数。采用的计算机为MacBook Air (处理器Intel Core i5-5250U 1.6 GHz,操作系统Windows 10企业版,编程语言MATLAB R2009a)。算例中给出的计算耗时为10次运行的平均值。为了对比,每个算例中都给出了原始多分辨率技术MRT-I[6]和MRT-II[7]的优化结果。二者的主要区别在于MRT-I在网格细化的每次迭代中添加一层高分辨率节点,而MRT-II则添加两层高分辨率节点。在所有算例中,参数p= 2,N1= 1,N2= 1。
4.1 算例1:Bryson-Denham问题
Bryson-Denham问题[6-7]又称最小能量控制问题,是典型的非光滑轨迹优化算例。该问题描述为求解最优控制u(t),使得如下目标函数最小
(14)
并且满足动力学方程
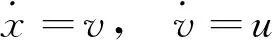
(15)
初始条件x(0) = 0,v(0) = 1,终端条件x(1) = 0,v(1) = 1;以及如下路径约束(状态变量边界约束)
x(t)≤l
(16)
式中:l为实数,本算例取l=0.04。
采用本文方法求解该问题,取N=8,Jmax=7,ε=10-3。IMRT迭代5次停止,图2给出优化结果。图2(a)为最优控制变量以及离散点分布,图中细实线为ENO插值结果,粗实线为解析解;图2(b)状态变量x随时间变化曲线,图中细实线为根据最优控制采用数值积分得到,粗实线为解析解。可见,本文方法从1025个均匀节点选取49个节点即可高精度逼近解析解。本文方法优化的目标函数11.11111101,与解析解(100/9)相差1.1×10-7。
对于该算例,若采用原始多分辨率技术求解(只细化控制变量的情况下),则会发生细化不充分。图3给出了采用MRT-I[6]优化的结果,可以看出,MRT-I只细化至W1,N就停止细化。由图3(a)可知,控制变量在切换点处的插值误差显然超过了误差限(10-3),因此MRT-I停止细化并不是因为精度达到要求,而是因为MRT-I本身缺陷造成的。MRT-I优化的目标函数11.09858462,与解析解相差1.3×10-2。
对比图2和图3可以发现,尽管离散节点细化不够充分引起的控制变量差异比较小,但是由此导致的状态变量差异却是显著的。更为重要的是, 如图3(b)中的局部放大图所示,对于受约束的状态变量x,尽管在离散点处均满足路径约束(式(16)),但是数值积分结果表明,在离散点之间x却违反了路径约束,x的峰值超出了路径约束上限0.5%。
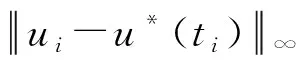
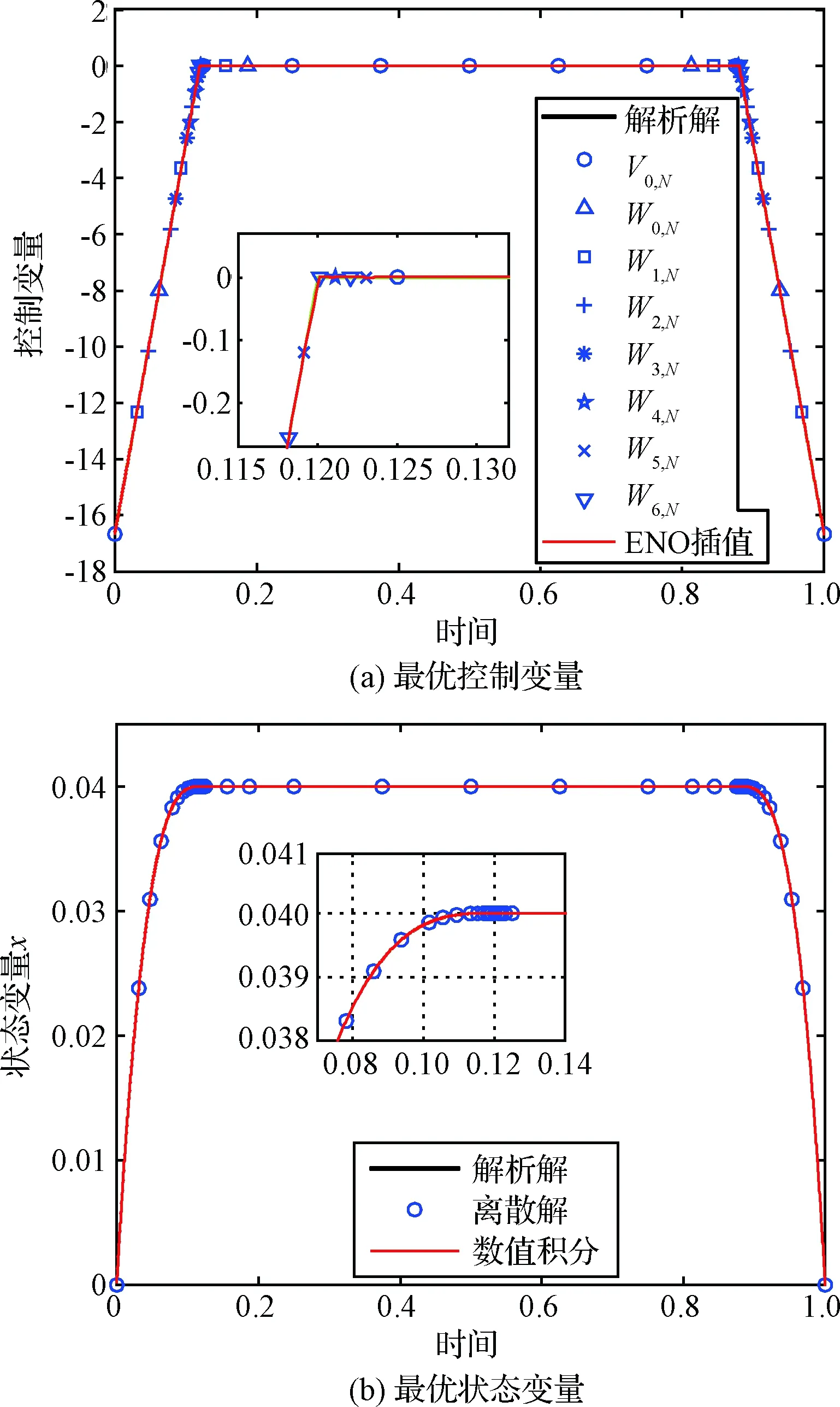
图2 IMRT优化的算例1最优解(49个节点)Fig.2 Solution for example 1 using IMRT (49 points)
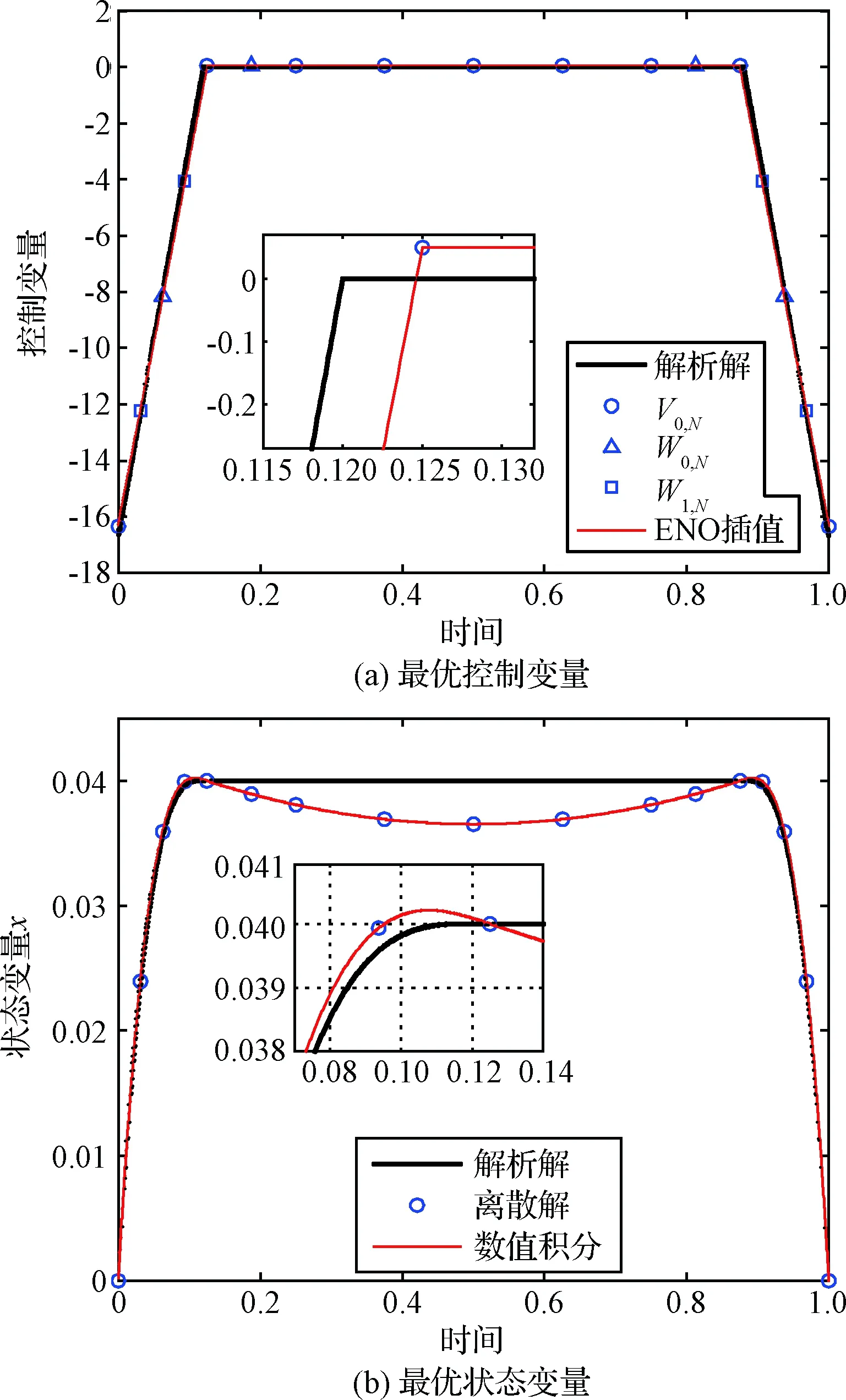
图3 MRT-I优化的算例1最优解(17个节点)Fig.3 Solution for example 1 using MRT-I (17 points)
了MRT细化不充分问题,但是由此带来的潜在问题包括:1)增加了算法复杂度,并且实际问题的控制量和状态量可能相差较大,需要分别选取误差限;2)需要更多的离散节点,对比表中MRT-II和本文方法可证实这一点;3)这种处理方法并非一直有效,参见文献[16]的论述和反例。此外,如前所述,文献[6-7]的方法要求初始节点数目必须为2j+1。文献[16]的方法突破了这一限制并且能够避免细化失败,但需要的网格细化迭代次数较多(见表1)。
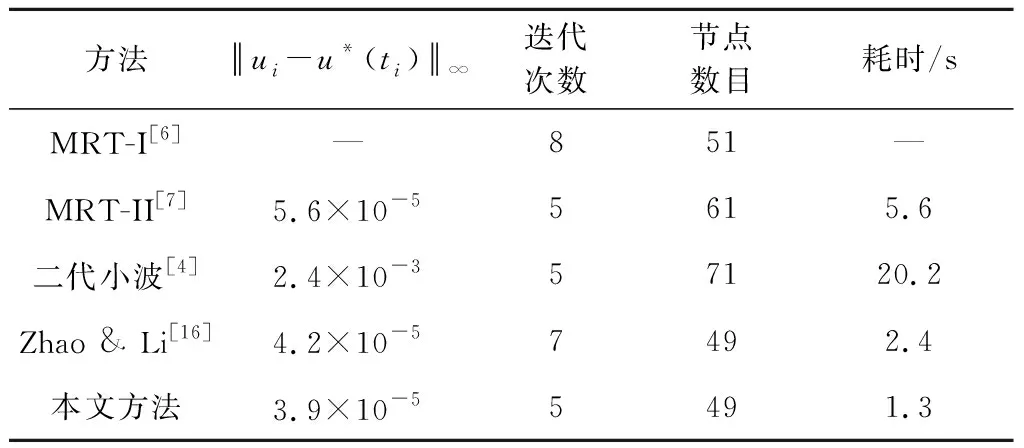
表1 不同方法求解算例1的效果对比Table 1 Solutions from different methods for example 1
4.2 算例2:最短时间轨道转移问题
本算例研究的最短时间小推力轨道转移问题是由小推力能量最优轨道转移问题简化而来,对于求解能量最优问题具有重要意义[18]。该问题的特色之处是其最优控制含有多个bang-bang切换结构,能够较好地检验改进多分辨率技术的有效性。
最短时间小推力轨道转移问题是通过优化飞行器的切向加速度和法向加速度,使飞行器从初始轨道转移至目标轨道消耗的时间最短。对于初始轨道和目标轨道均为圆轨道,问题描述如下[18]:
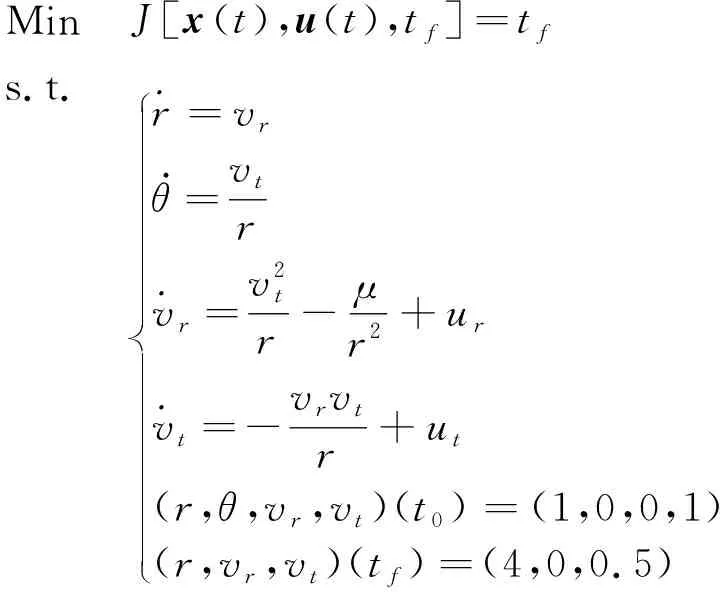
MinJ[x(t),u(t),tf]=tfs.tr = vrθ·=vtvr=v2tr-μr2+uvt=-vrvtr+ut(r,θ,vr,vt)(t0) = (1,0,0,1)(r,vr,vt)(tf)=(4,0,0.5)
(17)
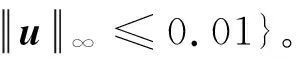
采用IMRT求解该问题,取参数N= 30,Jmax= 6,ε=2×10-4。注意本算例中特意选取N使其不等于2j(j为非负整数)。IMRT迭代4次中止,从最高分辨率节点V6, N的1921个均匀节点中选取153个离散节点,优化耗时1.5 s。图 4给出最优控制变量以及离散节点分布。由图4可知,本文方法在所有切换点处均达到预期的最高分辨率。本文方法优化的最优目标函数为47.699776 TU(文献[18]采用序列伪谱方法优化的目标函数为47.809 TU)。图5给出最优转移轨道,其中圆圈为离散最优解,细实线为根据图 4(a)所示的最优控制采用数值积分得到的结果。可见,飞行器虽然需要飞越多个周期才能达到目标轨道,但是仍然能够准确进入目标轨道。
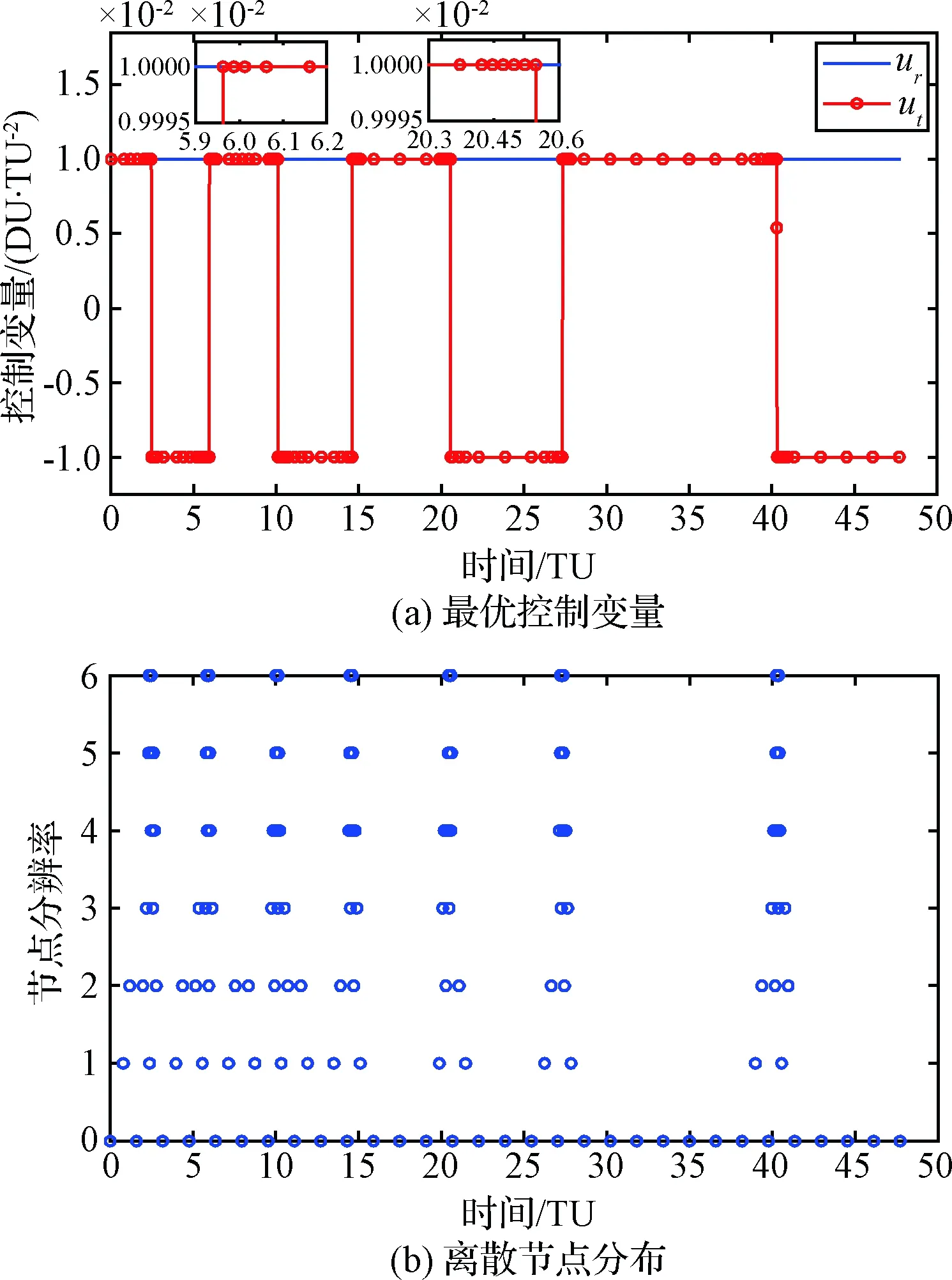
图4 IMRT优化的算例2最优解(153个节点)Fig.4 Solution for example 2 using IMRT (153 points)

图5 IMRT优化的算例2最优转移轨道Fig.5 Optimal transfer orbit for example 2 using IMRT
作为对比,图6给出采用MRT-I优化的控制变量和离散节点分布。从图6(b)所示的节点分布可以发现,在控制变量的第2个和第5个切换点处的离散节点并没有达到期望的最高分辨率。对比图4(a)和图 6(a)给出的控制变量局部放大插图可以发现,图6(a)中这两个位置的节点分布比图4(a)稀疏,并且二者的切换点位置也不完全一致,由此说明了图6(a)中这两个位置的控制变量细化不够充分。
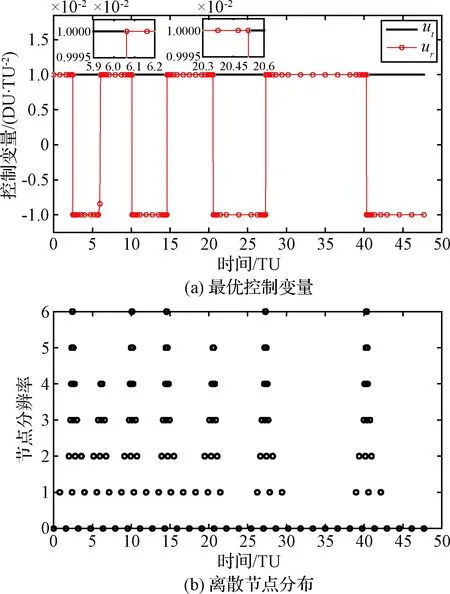
图6 MRT-I优化的算例2最优解(140个节点)Fig.6 Solution for example 2 using MRT-I (140 points)
MRT-I优化的最优目标函数为47.703654 TU,与IMRT的优化结果相差+0.008%。因此,对于本算例,这种节点细化不够充分对于目标函数几乎没有影响。但是,进一步研究表明,这种细化不充分却对终端状态变量的入轨误差有着显著影响。根据IMRT优化的控制变量,采用四阶龙格库塔方法对动力学系统进行积分,得到终端矢径、径向速度、切向速度的入轨误差分别为4.5×10-5,1.4×10-5,-3.0× 10-7;而根据MRT-I优化的控制变量积分动力学系统得到的终端入轨误差分别为-1.1×10-3,3.7×10-5,1.2×10-4。可见,IMRT优化的控制变量对应的入轨误差更小,即入轨精度更高。这是因为数值积分动力学系统时需要根据优化的离散控制变量插值计算各个积分点处的控制变量,IMRT优化的控制变量在所有切换点处都具有较高的分辨率,能够更加准确地插值出积分点处的控制变量,而MRT-I优化的控制变量在部分切换点处的分辨率不够高,在这些切换点处的插值误差更大,插值误差通过数值积分的累积效应影响终端入轨精度。
为了进一步分析本文的改进多分辨率技术的性能,表2给出了采用文献方法[6-7,16]求解该问题的结果对比。其中,MRT-I[6]和MRT-II[7]均发生了细化遗漏,Zhao&Li[16]方法和本文方法均避免了细化遗漏。由表2可知,与前述结论类似,是否发生细化遗漏对于该算例的目标函数影响微小,但是对于终端约束误差影响较大(未发生细化遗漏时终端状态的约束误差更小)。与MRT-I和MRT-II相比,本文方法避免了细化遗漏,终端约束误差更小,并且需要的网格迭代次数更少,优化耗时更短。与Zhao&Li方法相比,二者的终端约束误差相当,但是本文方法需要的网格迭代次数更少,因而耗时更短。
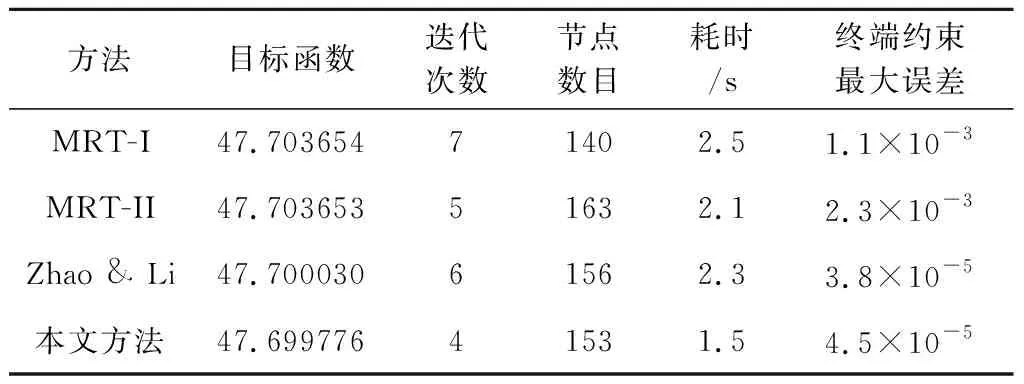
表2 不同方法求解算例2的效果对比Table 2 Solutions from different methods for example 2
4.3 算例3:航天器姿态调整问题
本算例采用改进多分辨率技术求解航天器的最优姿态调整问题。航天器为NASA的X射线计时探测器(XTE),优化目标使得航天器从一个姿态调整到另一个姿态消耗的时间最短。由于控制力矩大小恒定,因此时间最短等价于能量最省。
将航天器假设为刚体,采用四元数法描述的刚体航天器姿态动力学方程组如下[19]:
(18)
式中:q=[q1,q2,q3,q4]T为四元数,ω=[ω1,ω2,ω3]T为旋转角速度,u=[u1,u2,u3]T为控制力矩,转动惯量Ix=5621 kg·m2,Iy=4547 kg·m2和Iz=2364 kg·m2。
路径约束
(19)
控制变量约束
(20)
边界约束
(21)
目标函数
J[x(t),u(t),tf]=tf
(22)
采用IMRT求解该问题,取N=20,Jmax=7,ε=0.1。IMRT迭代5次中止,从最高分辨率节点V7, N的2561个均匀节点中选取121个离散节点,优化耗时4.3 s。图 7给出最优控制变量以及离散节点分布。可见,本文方法在所有切换点处均达到预期的最高分辨率。本文方法优化的目标函数为28.630403 s。
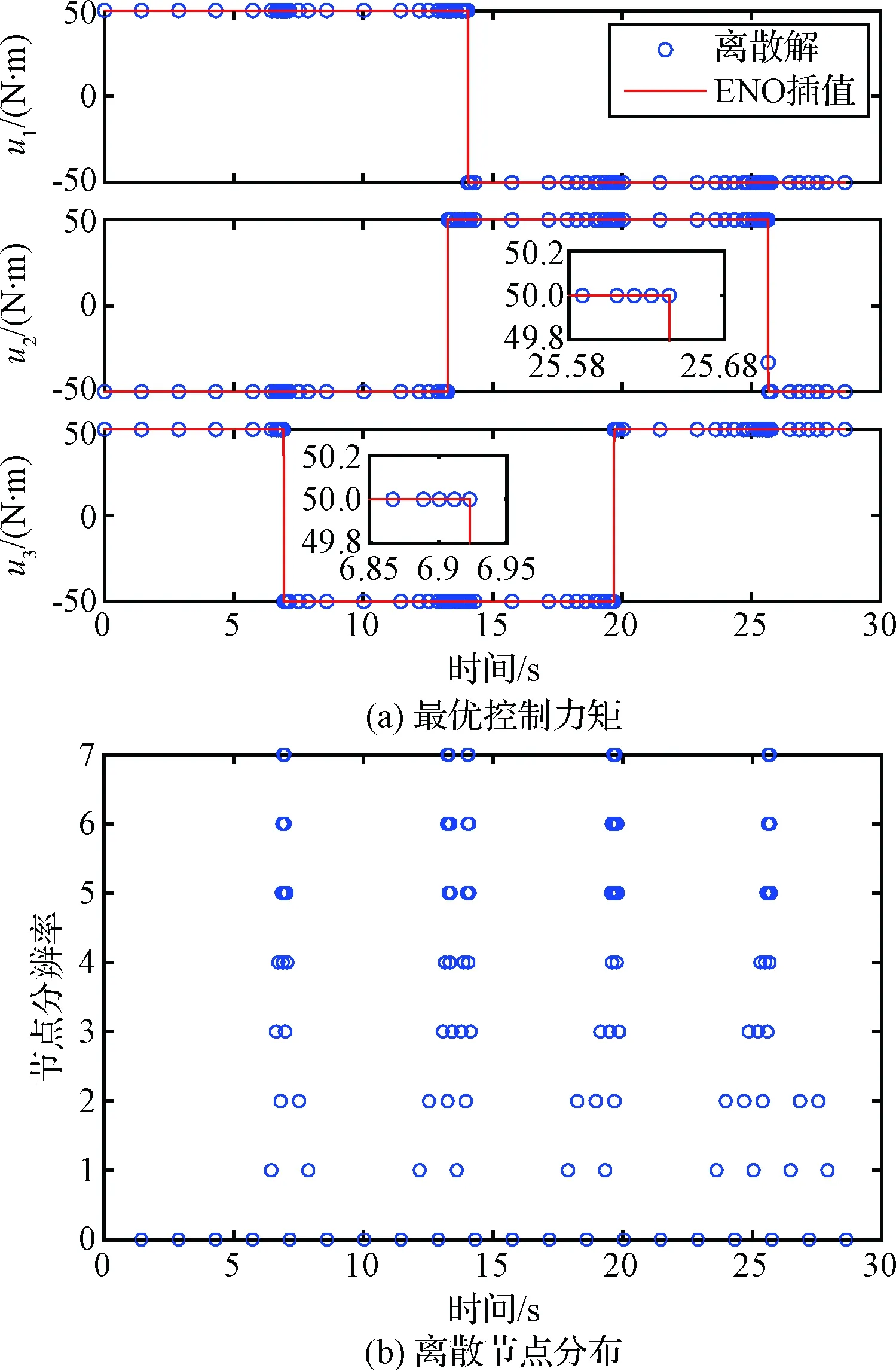
图7 IMRT优化的算例3最优解(121个节点)Fig.7 Solution for example 3 using IMRT (121 points)
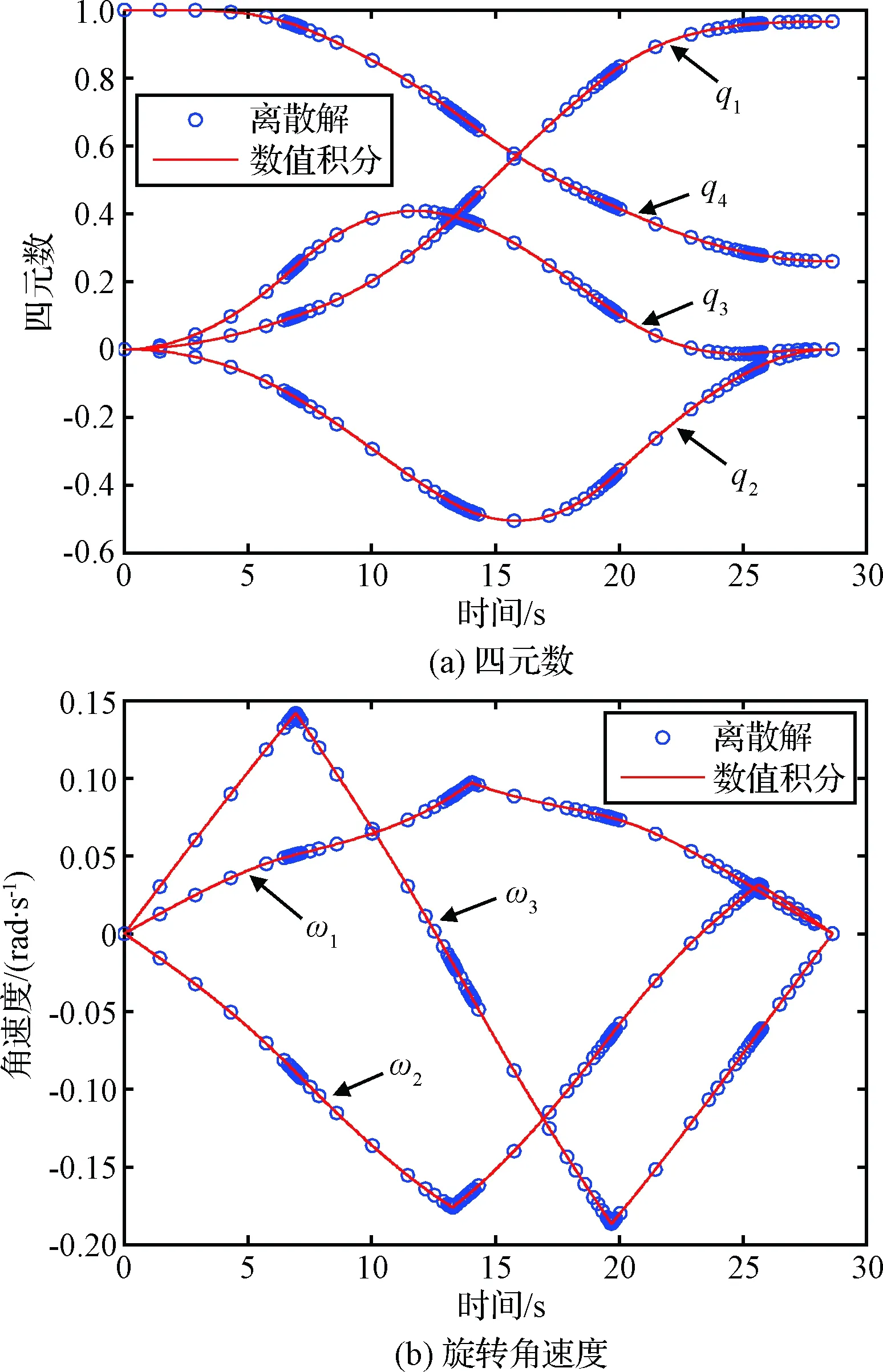
图8 IMRT优化的算例3最优状态变量Fig.8 State solution for example 3 using IMRT
图 8给出了优化的状态变量,其中圆圈为离散最优解,细实线为根据优化的最优控制变量采用四阶龙格库塔方法积分得到的结果。本算例的终端状态变量全部受到约束,数值积分结果表明,终端状态约束的误差分别为-3.6×10-6,-2.5×10-5,-2.8×10-5,1.4× 10-5,-2.7×10-6,-8.6×10-6,1.4×10-6。
作为对比,图 9给出了采用MRT-I优化的最优控制变量和节点分布,MRT-I优化的目标函数为28.630405 s。由图 9(b)可知,在控制变量的第一个和最后一个切换点处离散节点没有达到最高分辨率。对比图 7(a)和图 9(a)中的控制变量局部放大插图可以发现,MRT-I细化的节点分布中存在遗漏。对于该算例,这种细化遗漏对目标函数仍然几乎没有影响,但是根据MRT-I优化的控制变量对动力学系统积分,得到的终端状态约束的误差分别为2.1×10-5,5.8×10-4,-1.7×10-4,7.9×10-5,2.8×10-6,1.6×10-5,-1.3×10-4。可见,MRT-I得到的终端状态约束最大误差比IMRT的结果大一个量级以上。
表3给出采用本文方法和文献方法[4,6-7,16]求解该问题的结果对比。其中二代小波的结果来源于文献[4],最高分辨率为1921,其它方法的结果为本文采用文献中的方法计算得出,最高分辨率均为2561。MRT-I[6]和MRT-II[7]方法发生了细化遗漏,Zhao& Li[16]方法和本文方法避免了细化遗漏,二代小波算法不确定是否发生细化遗漏。可见,与算例2类似,是否发生细化遗漏对于目标函数影响微小,但是对于终端约束误差影响显著。该算例再次表明,本文方法与其它多分辨方法相比需要的网格迭代次数和离散节点数目较少(优化耗时更短),并且能够避免细化遗漏问题(终端约束误差更小)。
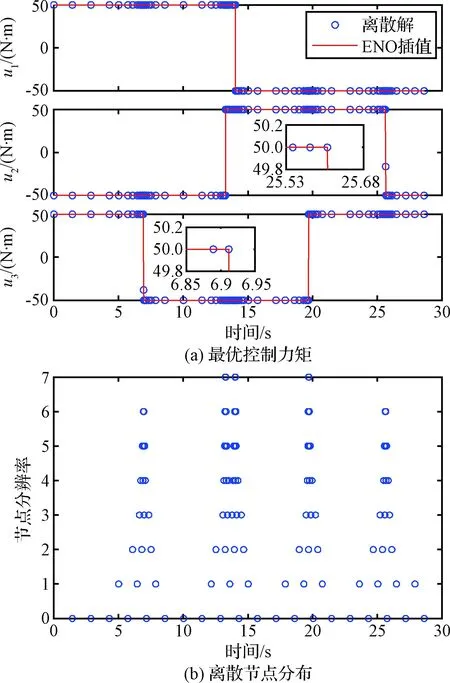
图9 MRT-I优化的算例3最优控解(110个节点)Fig.9 Solution for example 3 using MRT-I (110 points)
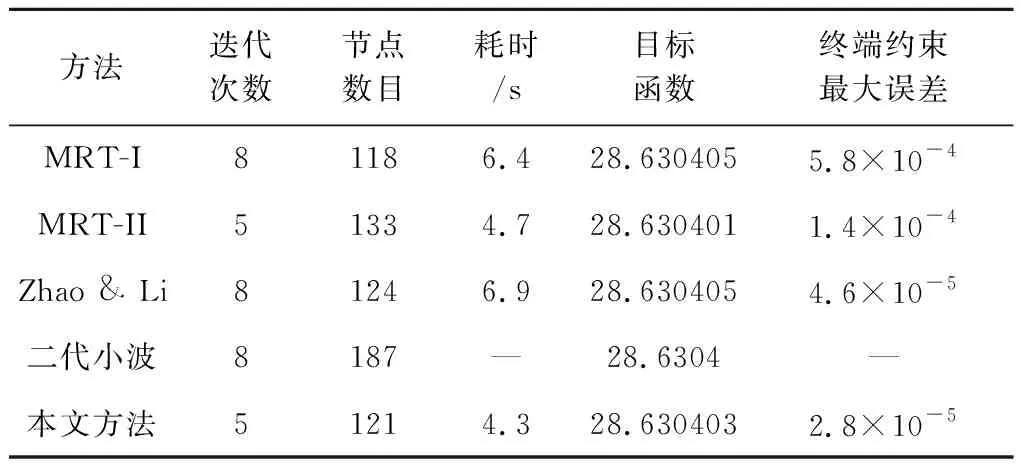
方法迭代次数节点数目耗时/s目标函数终端约束最大误差MRT-I81186.428.6304055.8×10-4MRT-II51334.728.6304011.4×10-4Zhao & Li81246.928.6304054.6×10-5二代小波8187—28.6304—本文方法51214.328.6304032.8×10-5
5 结 论
本文提出一种改进多分辨率方法用于求解非光滑轨迹优化问题。针对原始多分辨率技术在网格细化过程中可能会发生细化遗漏或者失败的缺陷,本文通过在网格细化过程中增加节点检测算法确保在每个插值误差较大的离散节点附近网格达到当前迭代的最高分辨率。为了进一步提高网格细化效率,该方法在每次细化时添加两层高分辨率节点,从而减少网格细化迭代的次数。此外,针对原始多分辨率技术的初始网格节点数目必须是2j+1(j是非负整数)的限制,定义了一种新的广义二分网格,使得初始节点数目可以为任意奇数而不限于2j+1。采用多个非光滑轨迹优化算例验证了方法的有效性和特色。结果表明,本文方法能够在轨迹的非光滑区域持续细化网格,避免了细化遗漏或者失败,并且具有较高的细化效率。此外,研究发现,本文方法避免细化遗漏对于目标函数影响不大,但是却能够更加准确地满足路径约束和终端状态约束。
参 考 文 献
[1] 雍恩米, 陈磊, 唐国金.飞行器轨迹优化数值方法综述[J]. 宇航学报, 2008, 29(2): 397-406. [Yong En-mi, Chen Lei, Tang Guo-jin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics, 2008, 29(2): 397-406. ]
[2] 赵吉松. 求解轨迹优化问题的局部配点法的稀疏性研究 [J]. 宇航学报, 2017, 38(12): 1263-1272. [Zhao Ji-song. Exploiting sparsity in local collocation methods for solving trajectory optimization problems [J]. Journal of Astronautics, 2017, 38(12): 1263-1272.]
[3] Betts J T, Huffman W P. Mesh refinement in direct transcription methods for optimal control [J]. Optimal Control Applications and Methods, 1998, 19(1): 1-21.
[4] 丰志伟, 张青斌, 唐乾刚, 等. 基于二代小波的轨迹优化节点自适应加密 [J]. 航空动力学报, 2013, 28(7): 1659-1665. [Feng Zhi-wei, Zhang Qing-bin, Tang Qian-gang, et al. Node adaptive refinement for trajectory optimization based on second-generation wavelets [J]. Journal of Aerospace Power, 2013, 28(7): 1659-1665.]
[5] Assassa F, Marquardt W. Dynamic optimization using adaptive direct multiple shooting [J]. Computers and Chemical Engine-ering, 2014, 60(2): 242-259.
[6] Jain S, Tsiotras P. Multiresolution-based direct trajectory optimization [C]. The 46th IEEE Conference on Decision and Control, Piscataway, USA, Dec 12-14, 2007.
[7] Jain S, Tsiotras P. Trajectory optimization using multiresolution techniques [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1424-1436.
[8] 陈小庆, 侯中喜, 刘建霞. 基于多分辨率技术的滑翔飞行器轨迹优化算法 [J]. 宇航学报, 2010, 31(8): 1944-1950. [Chen Xiao-qing, Hou Zhong-xi, Liu Jian-xia. A multiresolution technique-based gliding vehicle trajectory optimization algorithm [J]. Journal of Astronautics, 2010, 31(8): 1944-1950.]
[9] 赵吉松, 谷良贤, 佘文学. 配点法和网格细化技术用于非光滑轨迹优化 [J]. 宇航学报, 2013, 34(11): 1442-1450. [Zhao Ji-song, Gu Liang-xian, She Wen-xue. Application of local collocation method and mesh refinement to nonsmooth trajectory optimization [J]. Journal of Astronautics, 2013, 34(11): 1442-1450. ]
[10] Zhao Y, Tsiotras P. Density functions for mesh refinement in numerical optimal control [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(1): 271-277.
[11] 张志国, 余梦伦, 耿光有, 等. 应用伪谱法的运载火箭在线制导方法研究 [J]. 宇航学报, 2017, 38(3): 262-269. [Zhang Zhi-guo, Yu Meng-lun, Geng Guang-you, et al. Research on application of pseudo-spectral method in online guidance method for a launch vehicle [J]. Journal of Astronautics, 2017, 38(3): 262-269.]
[12] Ross I M, Fahroo F. Pseudospectral knotting methods for solving optimal control problems [J]. Journal of Guidance, Control, and Dynamics, 2004, 27(3): 397-405.
[13] Darby C L, Hager W W, Rao A V. Direct trajectory optimization using a variable Low-order adaptive pseudospectral method [J]. Journal of Spacecraft and Rockets, 2011, 48(3): 433-445.
[14] Patterson M A, Hager W W, Rao A V. A ph mesh refinement method for optimal control [J]. Optimal Control Applications and Methods, 2015, 36(4): 398-421.
[15] Liu F, Hager W W, Rao A V. Adaptive mesh refinement method for optimal control using nonsmoothness detection and mesh size reduction [J]. Journal of the Franklin Institute-Engineering and Applied Mathematics, 2015, 352(10): 4081-4106.
[16] Zhao J, Li S. Modified multiresolution technique for mesh refinement in numerical optimal control [J]. Journal of Guidance, Control, and Dynamics, 2017, 40(12): 3328-3338.
[17] Harten A, Engquist B, Osher S, et al. Uniformly high order accurate essentially non-oscillatory schemes III [J]. Journal of Computational Physics, 1997, 131(1): 3-47.
[18] Ross I M, Gong Q, Sekhavat P. Low-thrust, high-accuracy trajectory optimization [J]. Journal of Guidance, Control, and Dynamics, 2007, 30(4): 921-933.
[19] Fleming A, Sekhavat P, Ross I M. Minimum-time reorientation of a rigid body [J]. Journal of Guidance, Control, and Dyn-amics, 2010, 33(1): 160-170.
[20] Gill P E, Murray W, Saunders M A. SNOPT: An SQP algorithm for large-scale constrained optimization [J]. SIAM Journal on Optimization, 2002, 12(4): 979-1006.
[21] Csendes T. Developments in reliable computing [M]. Dordrecht: Kluwer Academic Publishers, 1999.
