单模激发纠缠态的纠缠度

许 兰

(湖南第一师范学院 教育科学学院，湖南 长沙，410205)

自从1993 年由Bennett 等人提出量子隐形传态协议开始，量子纠缠被作为一种量子资源而引起人们的广泛关注，量子纠缠也成为了量子信息与量子计算领域的一个非常热门的研究课题。众所周知，爱因斯坦将量子纠缠称为“鬼魅的超距作用”(spooky action at a distance)。例如，有两个相互纠缠的粒子，即使相距非常遥远的距离，一个粒子的行为将会影响另一个粒子的状态，同时，当其中一个粒子被操作而状态发生变化时，另一个粒子也会立即发生相应的状态变化，这就是量子纠缠。量子纠缠是量子计算[1-2]和量子通信[3-8]的重要资源，有些量子任务的处理是完全基于量子纠缠的，而有些任务会因为量子纠缠而变得更加有效。

纠缠相干态是实现连续变量量子信息处理的纠缠态之一。因此，产生和操纵量子纠缠态成为了量子信息应用中的基本问题，值得大家进一步探讨。近年来，连续变量纠缠态的量子特性及其在量子计算和量子信息中的应用也引起了大家的关注[9-20]。对量子纠缠的定量描述也是量子信息理论研究的热点问题，如果要知道待研究的量子纠缠态携带纠缠的量的多少，那就需要确定量子纠缠态的纠缠度。 对纠缠度进行描述，实质上是为了对不同的纠缠态之间建立定量的可比关系。

文中研究了单模激发纠缠相干态(SMEECSs)的纠缠度并谈论单模光子激发对单模激发纠缠相干态(SMEECSs)的纠缠度的影响。最后进行了总结。

1 单模激发纠缠相干态的纠缠度

文章的这一部分主要研究单模激发纠缠相干态(SMEECSs)的纠缠度。单模激发纠缠相干态 SMEECSs定义为

(1)

直接可以计算出(1)式中的归一化常数为

(2)

这里Lm(x)为m阶拉盖尔多项式，定义为

(3)

如(1)式单模激发纠缠相干态(SMEECSs)是双元纠缠态，而两态纠缠态的量子纠缠度可以用(concurrence) 来量度[19-20]，根据文献[21]，通常把分离变量纠缠态的定义为

=|〈Ψ|σy⊗σ|Ψ*〉|

(4)

这里|Ψ*〉是|Ψ〉的复共轭。=1，这时的纠缠态被称为最大纠缠态。

考虑一个一般的，形如(1)式中的连续变量纠缠态

|Ψ=μ|η〉⊗|γ〉+v|ξ〉⊗|δ〉

(5)

这里|η〉和|ξ〉是子系统1的两个归一化态，|γ〉和|δ〉是子系统2的两个归一化态。μ和v是复数。归一化后，纠缠态|Ψ〉可写成如下的形式

(6)

其中归一化常数由下式给出

(7)

通过连续变量形式的转化组成分离正交基矢，并利用 Schmidt 分解式[22]，容易得出纠缠态 (5) 的纠缠度

(8)

从没有光子激发双模纠缠相干态ECSs (i.e.，m=0)开始，ECSs为

|Ψ±(α,0)〉=N±(α,0)(|α,α〉±|-α,-α〉)

(9)

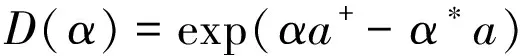
(10)

利用方程(9)和(10)，根据方程(6)、(7)和(8)中可以得出其纠缠度为

(11)

上式意味着ECS|Ψ-(α,0)〉的纠缠度独立于状态参量α，并且它是最大纠缠态，这时ECS|Ψ+(α,0)〉的纠缠度比ECS|Ψ-(α,0)〉的纠缠度小，ECS|Ψ+(α,0)〉的纠缠度随着状态参量α的值增大而增大。同时，文中作出了单模激发纠缠相干态(SMEECSs)纠缠度+(α,m)随参量的变化曲线(如图1)，图中看出纠缠度+(α,m)随的增大而增大。

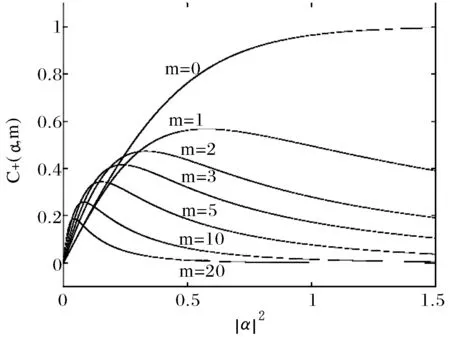
图1 当m=0,1,2,3,5,10,20时，单模激发纠缠相干态(SMEECSs)|Ψ+(α，m)〉的纠缠度+(α,m)随参量的变化曲线Fig.1 The concurrence of the SMEECS|Ψ+(α,m)〉versus for the different photon excitations with m=0，1，2，3，5，10，and 20，respectively

当存在光子激发的时候，即m≠0，根据(1)式，这时单模激发纠缠相干态(SMEECSs)代入(7)式和(8)式可以得到相应的纠缠度是

(12)

(13)

2 光子激发对单模激发纠缠相干态纠缠度的影响

为了讨论光子激发在光场的不同光强区对单模激发纠缠相干态(SMEECSs)|Ψ+(α,m)〉的量子纠缠的影响，在图1中作出了+(α,m)在不同光激发数m的情况下,随参量的变化曲线。图1说明单模激发纠缠相干态(SMEECSs)在光场的不同光强区有着不同的纠缠特性。从图1中可以看见每一条单模激发纠缠相干态|Ψ+(α,m)〉m≠0的纠缠度曲线都存在一个峰。这些峰随着光激发数m的增加峰向左移，而峰的高度随着光子激发数m的增加是降低的。在这些峰的左手边部分随着光强度的增加纠缠度也会增大，而右手边的部分随着光强度的增加纠缠度是减小的。在弱的场区，SMEECS的纠缠度表现出有趣的性质。为了把这些表现出来，在图2 中作出了+(α,m)在弱场区<0.03随不同光子激发数m变化的纠缠度曲线。可以发现随着光激发数m的增加纠缠度是增大的，同时随着光强度呈线性增大。通过分析这些结果可以确定，事实上，在弱场区<0.03的情况下，通过方程 (13) 可以近似地得到纠缠度。

图2 当m=0，1,2,3,5,10,20时，在弱场区<0.03单模激发纠缠相干态(SMEECSs)|Ψ+(α,m)〉的纠缠度+(α,m)随参量的变化曲线Fig.2 The concurrence of the SMEECS |Ψ+(α,m)〉 in the weak field regime of <0.03 versus for the different photon excitations with m=0，1，2，3，5，10，and 20，respectively

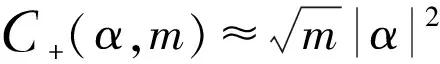
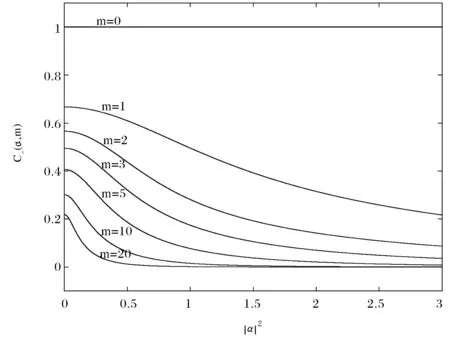
图3 当m=0,1,2,3,5,10,20时，单模激发纠缠相干态(SMEECSs)|Ψ-(α,m)〉的纠缠度-(α,m)随参量的变化曲线Fig.3 The concurrence of the SMEECS |Ψ-(α,m)〉 versus for the different photon excitations with m= 0，1，2，3，5，10，and 20，respectively

3 小结

文章介绍了一种连续变量的纠缠相干态—单模激发纠缠相干态(SMEECSs)。研究了这一量子纠缠态携带纠缠的量的多少—纠缠度，并研究了光子激发数对单模激发纠缠相干态(SMEECSs)的纠缠度的影响。近年来，围绕量子纠缠所作的研究工作是方方面面的，如：量子纠缠的定性和定量，量子纠缠态的制备和储存，量子纠缠的操作和控制等。随着量子纠缠这一重要的量子资源的不断应用，量子纠缠的优越性将进一步体现，值得大家在以后的工作中作更加深入的研究。

参考文献:

[1]DIVINCENZO D P.Quantum computation[J].Science，1995，270(10):255-261.

[2]GROVER L K.Quantum Mechanics Helps in Searching for a Needle in a Haystack[J].Physical Review Letters，1997，79(02):325-328.

[3]BENNETT C H，BRASSARD G，CREPEAU C,et al.Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J].Physical Review Letters，1993，70(13):1895-1899.

[4]BOUWMEESTER D，PAN J W，MATTLE K，et al.Experimental quantum teleportation[J].Quantum Entanglement & Quantum Information-Ccast，1999，390(390):575-579.

[5]BENNETT C H,WIESNER S J.Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states[J].Physical Review Letters，1992，69(20):2881-2884.

[6]MATTLE K，WEINFURTER H，KWIAT P G，et al.Dense Coding in Experimental Quantum Communication[J].Physical Review Letters，1996，76(25):4656-4659.

[7]BENNETT C H，BRASSARD G，MERMIN N D.Quantum cryptography without Bell’s theorem[J].Physical Review Letters，1992,68(05):557-559.

[8]GIOVANNETTI V，LLOYD S，MACCONE L.Positioning and clock synchronization through entanglement[J].Physical Review A，2001,65(02):130-132.

[9]BRAUNSTEIN SL ,LOOCK PV.Quantum information with continuous variables[J].Reviews of Modern Physics,2005，77(2):513-577.

[10]JEONG H ,KIM M S.Efficient quantum computation using coherent states[J].Physical Review A，2002，65(04):579.

[11]ENK S，HIROTA O.Entangled coherent states:Teleportation and decoherence[J].Physical Review A，2000，64(02):022313.

[12]BAN M.Quantum dense coding via a two-mode squeezed-vacuumstates[J].Journal of Optics B Quantum & Semiclassical Optics，1999，1(06):L9-L11.

[13]FURUSAWA A，KIMBLE H J，GEORGIADES NP,et al.Teleportation of Continuous Quantum Variables[J].Physical Review Letters，1998，80(04):133.

[14]FURUSAWA A,SORENSEN JL，BRAUNSTEIN SL .Unconditional quantum teleportation[J].Science，1998，282(5389):706.

[15]KUANG L M，ZHOU L.Generation of atom-photon entangled states in atomic Bose-Einstein condensate via electromagnetically induced transparency[J].Physical Review A，2012,68(04):043606.

[16]ZHOU L ，KUANG L M.Linear Optical Implementation for Quantum Teleportation of Unknown Two-Qubit Entangled States[J].Chinese Physics Letters，2004，21(11):2101-2104.

[17]ZHOU L ,KUANG L M.Proposal for optically realizing a quantum game[J].Physical Review A，2003，315(06):426-430.

[18]LU J，ZHOU L，KUANG L M.Liner optics implementation for quantum game with two players[J].Physical Review A，2004，330(1-2):48-53.

[19]WANG Y T，TANG J S,HU G，et al.Experimental Demonstration of Higher Precision Weak-Value-Based Metrology Using Power Recycling[J].Physical Review Letters，2016,117(23):230801.

[20]WEI C P，HU X Y，YU YF ,et al.Phase sensitivity of two nonlinear interferometers with inputting entangled coherent states[J].Chinese Physics B，2016，25(04):74-78.

[21]HILL S，WOOTTERS W K.Entanglement of a Pair of Quantum Bits[J].Physical Review Letters,1997，78(26):5022-5025.

[22]WANG X.Quantum teleportation of entangled coherent states[J].Physical Review A,2001,64(02):29-32.