脉冲效应对地下管廊地震响应的影响

2018-07-02李铎，周晶

水利与建筑工程学报 2018年3期

李铎，周晶

(大连理工大学建设工程学部，辽宁大连 116024)

不同地震类型对结构地震响应的影响至关重要。从以往观测的地震纪录来看，即使是中等强度的地震，含脉冲效应的地震仍然会对结构造成极大的破坏[1]。相比于非脉冲型地震，脉冲型地震因含有明显的速度脉冲及由此产生的大位移，导致地震能量在短时间内释放，从而更易对结构造成破坏。

Bertero V V等[2]于1978年提出在进行结构抗震设计时应该考虑近场地震的影响，但并未说明近场地震扩大结构响应的机理。1985年Housner和Hudson对Port Hueneme地震获得的纪录时程曲线进行研究时发现了近场地震脉冲效应[3]。从此结构在脉冲效应影响下的研究逐步开展起来。关于脉冲效应对结构的影响多集中在地面结构[4-9]。现如今地面结构的抗震研究已达到了实用阶段，如我国已制定大量地面建筑抗震设计规范。地面结构与地下结构比较来看，前者在荷载作用下以剪切变形和弯曲变形为主，后者因其周围岩土介质将大量高频地震成分吸收，使结构受到地震作用减少，但是当地下结构存在明显的惯性或土-结构间的刚度失配时，地下结构会因过度变形导致破坏[10]。而对于地下结构特别是近几年兴起的城市地下综合管廊的抗震研究成果较少。且中国尚未出台管廊的抗震设计规范。已有的关于地下管廊地震响应分析，在强震选取方面则多选用比较著名的地震波，较少从脉冲地震角度进行深入分析。

本文选取城市地下综合管廊作为研究对象，基于ABAQUS有限元分析软件及Python程序语言建立了脉冲地震作用下三维无限元城市地下综合管廊模型，采用等效荷载形式加载地震波作用，由选择的近场脉冲地震反应谱拟合出远场地震波，计算了远/近场地震作用下管廊的动力响应。分析了脉冲效应对结构地震响应的影响。该结果对管廊抗震设计具有参考意义。

1 计算方法和原理

1.1 无限元边界

无限元在动力分析中充当了吸收边界的角色，ABAQUS中的无限元参考了黏性边界的工作[11]，并结合了无限元静力人工边界。在涉及到无穷远边界的动力分析中，人工截断边界最大的问题在于波会在边界界面上反射，将部分能量重新传回网格，但在实际情况中波是向无穷远继续传播的。所以，需要将传入有限元区域的波吸收掉。

针对无限单元，Lysmer和Kuhlemeyertu推导出的三维下纵波和横波的阻尼系数分别为：

(1)

式中：G为剪切模量；cp和cs分别为纵波和横波波速。

只要使无限元的阻尼常数符合上式，人工边界就可以完全吸收边界处的反射波，从而起到模拟无限域辐射阻尼的作用[12]。

1.2 地震P波入射

本文在文献[13-16]的基础上推导了针对无限元边界的等效荷载。因为无限单元的特殊构造，从而不需要考虑弹性力，因此等效荷载的表达式如下：

(2)

以入射P波为例，推导其在底面产生的竖直方向(z方向)的地震波等效应力表达式。入射P波引起的节点的位移表达式为：

(3)

当P波入射时，θ1和θ2分别为入射波P波和反射SV波与z轴的夹角，如图1所示。α是入射波与反射波确定的平面与x轴的夹角。

图1 P波入射示意图

根据弹性力学[17]，竖向应力分量的物理方程为：

(4)

式中：

(5)

(6)

(7)

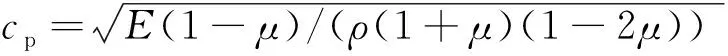
(8)

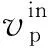
(9)

vp为入射P波的速度时程。所以入射P波对底面计算点产生的竖直向力为：

(10)

同理，可以得到无限地基中五个面上节点的等效荷载具体表达式。

底面(外法向为z轴负方向)的节点等效力：

(11)

(12)

(13)

式中：A2/A1为反射P波放大系数，B2/A1为反射SV波放大系数[15]。对于本文，仅采用P波垂直入射，故θ1=θ2=0°，α=0°，B2/A1=0，A2/A1=-1。上式变为：

(1) 底面(外法向为z轴负方向)的边界面节点等效力：

(14)

其他方向上的力：

(2) 左侧边界面(法线方向为y轴负方向)

(15)

(3) 右侧边界面(法线方向为y轴正方向)

(16)

(4) 后侧边界面(法线方向为x轴负方向)

(17)

(5) 前侧边界面(法线方向为x轴正方向)

(18)

式中：Δt1，Δt2分别为入射P波和反射P波传播至计算点的时间。

该垂直入射结果与黄胜[14]推导出的等效应力结果相同，具有一定正确性。而斜入射公式及其推导过程具有更强的适用性。

1.3 等效荷载垂直入射算例验证

对三维无限元人工边界的地震动等效荷载输入方式进行验证。图2(a)所示为三维线弹性半空间模型，模型尺寸44 m×44 m×37 m(长×宽×高)，有限元网格尺寸为1 m，四周及底部无限单元厚度均为3 m。材料参数为：弹性模量E=180 MPa，泊松比v=0.3，密度ρ=1 900 kg/m3。入射波位移时程如图2(b)所示。

图2验证模型及验证波

图3给出了P波垂直入射时模型顶部中心点A和底部中心点B的竖向位移时程。

图3 P波垂直入射竖向位移结果

可以看出顶部中心点A的位移峰值是底部点B位移峰值的2倍，这与弹性介质中波传播过程的理论解结论一致。故该方法可以用于模拟无限地基中地震波的传播规律。

1.4 地震波选择

本文基于加州大学伯克利分校太平洋地震工程研究中心的PEER地震动数据库，根据设计反应谱得到三条速度脉冲纪录，并将其峰值加速度均调整为0.2g，然后采用人造地震动反应谱的非线性拟合方法[18-19]，分别根据脉冲地震反映谱拟合相同加速度峰值的非脉冲地震，将其分为三组分别进行对比，可以较全面的分析地震波的频谱特性和脉冲效应对结构地震响应的影响。以第二组为例，原始地震波及拟合地震波的速度时程如图4所示。脉冲地震与拟合地震的参数如表1所示。

表1 脉冲地震及拟合地震参数

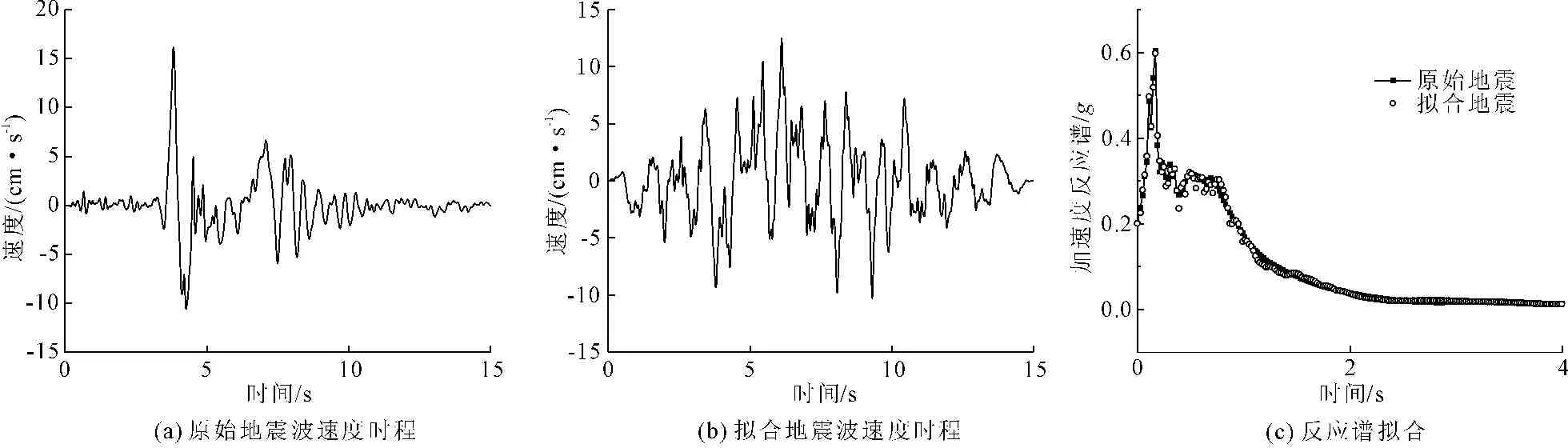
图4模拟时程反应谱与目标反应谱的拟合情况

2 算例信息

本文地下综合管廊以某实际工程为研究对象。该管廊为双孔钢筋混凝土结构，截面尺寸为4.5 m×3.0 m，长度方向取20 m。管廊顶部覆土厚度为3 m。左侧廊道净宽2.5 m，净高2.5 m，内设直径0.4 m排水管道，管道中心距右侧墙壁0.7 m，混凝土内部嵌入钢筋。按照地下结构的有限元分析理论。有限元模型两侧土体宽度取为管廊结构宽度的4倍，土体向下取为管廊高度的6倍。

该地区抗震设防烈度为8度，设计地震分组为第一组，基本地震加速度峰值为0.2g。

混凝土采用CDP损伤本构。具体材料参数如表2所示。考虑管廊结构与土体之间的相互作用，建立的三维有限元模型如图5所示。为便于观测管廊结构在地震作用下的动力响应，在管廊截面上选择若干点作为观测点。管廊具体尺寸与所选测点位置如图6(a)所示。

图5三维有限元边界计算模型

3 计算结果与分析

3.1 综合管廊纵向位移动力响应分析

将结构按长度方向从左右两个廊道顶板及地板处各取7个点，如图6(b)所示，然后左侧利用A点和D点竖向位移，右侧利用B点和C点竖向位移，观察其沿长度方向左右两侧的竖向相对位移变化，见图7。

由图7可以看出：第一，在相同位置处，近场脉冲地震作用下的结构竖向相对位移均大于远场地震，说明在相同峰值加速度情况下，速度脉冲地震对结构的地震响应有放大的效应；第二，在长度方向上地震动产生的侧向位移发展分两段，呈阶梯状成长，这与模型的外边界固定设置有关；第三，位移响应在前后面出现对称结果，由于本文采用垂直入射，使结构各点在震动中的相位差很小。对于管线结构，如果地震入射为非一致激励，会因为距离较远产生相位差而对不同部位造成不同的影响。

表2 材料参数

图6 模型尺寸及测点示意图

图7结构两侧竖直向相对位移

3.2 结构应力分布情况

对于混凝土结构，多选用拉应力衡量其破坏情况。本文选取结构中部截面研究结构在地震作用下的动力响应，在结构截面不同部位选取13个点观测结构的最大拉应力分布情况。测点位置如图6(a)所示。

最大拉应力结果如图8所示。可以看出：第一，结构在脉冲地震作用下的拉应力均大于非脉冲地震，说明脉冲地震会放大结构的动力反应，这与上一节得到的结论相同；第二，由不同部位的应力大小可以看出，最大主应力值随监测点的位置呈现自下而上逐渐增大的趋势，结构顶部(A、B、C、D、E点)所受应力总体上略大于左右边墙及中墙(F、H、G点)受到的应力，而结构底部(I、J、L、L、M点)的应力最小，所以双孔管廊的顶部为抗震薄弱点，易于发生破坏；第三，对比应力结果及三组地震峰值速度可知，在峰值加速度相同的情况下，峰值速度越大，结构响应越大。

图8截面不同部位最大主应力峰值

3.3 不同时刻拉伸损伤因子分析

为了说明脉冲地震对管廊的破坏演化过程，数值分析中输出了几个关键时刻管廊结构混凝土拉伸损伤因子值(DAMAGET)分布云图[20]，如图9所示。

图9混凝土损伤演化过程

从图9可以看出地震作用下管廊破坏的演化过程。当t=3.78 s时，结构左侧顶板开始出现拉伸裂缝。当t=3.84 s时，顶部裂缝基本贯穿整个横截面，该部位混凝土基本丧失抗拉强度和竖向抗剪强度。当t=4.45 s时裂缝已扩展至中墙顶部。t=6.62 s时，破坏持续向中墙顶部及右侧廊道扩展。由于左侧顶板已丧失强度，导致顶板覆土压力向中墙及右侧顶板转移，故当t=7.0 s时，中墙顶部和右侧顶板发生压碎和剪切破坏，并且破坏逐渐贯穿整个顶部。最后，当t=15 s时，损伤传播至左右边墙顶部，整个结构上部均遭到破坏。从损伤演化过程看，左侧顶板的破坏是结构破坏的主要原因。

结合3.3节图8(b)，PUL194地震波在左侧廊道顶部产生的最大拉应力为2.15 MPa，而该C35混凝土的轴心抗拉强度设计值为2.20 MPa。考虑静力与地震荷载的组合，其拉应力将超过设计强度。这与上面所分析的左侧廊道顶部产生拉伸破坏吻合。

从时间上看，该条地震波在3.7 s左右突然产生速度脉冲效应，短时间内释放大量能量。而结构也是从该时刻起开始产生破坏。再一次说明脉冲效应增加了结构的动力响应，在设计时应该予以重视。

4 结论

本文分析了地下管廊结构在脉冲地震和非脉冲地震作用下的动力响应，得到以下结论：

(1) 具有速度脉冲效应的纪录会在短时间释放大量的地震能量，使地基产生大变形。导致结构在地基约束下产生破坏。在进行地下管廊抗震分析时应该考虑脉冲地震的影响，否则将会放大管廊的抗震性能，对管廊在近场脉冲地震作用下的抗震不利。

(2) 在相同地震峰值加速度下，不同峰值速度对结构动力响应也产生不同的影响。速度脉冲越大，结构响应越大，这是因为大速度会引起土体的大位移，而使结构产生大的变形。

(3) 根据本文的分析，在竖向地震作用下，该工程中的薄弱部位在管廊顶部。在实际情况中，地下结构在地震作用下也多因顶板开裂、坍塌而引起破坏。计算结果与事实相符。所以在管廊结构设计时应当重点考虑管廊顶板部位。

参考文献：

[1] 耿方方,丁幼亮,谢辉,等.近断层地震动作用下长周期结构的地震动强度指标[J].东南大学学报(自然科学版),2013,43(1):203-208.

[2] Bertero V V, Mahin S A, Herrera R A. Aseismic design implication of near-fault San Fernando earthquake records[J]. Earthquake Engineering and Structural Dynamics, 1978,6(1):31-42.

[4] 陈令坤,张楠,胡超,等.近断层地震方向脉冲效应对高速铁路桥梁弹塑性反应的影响[J].振动与冲击,2013,32(15):149-155，167.

[5] Chen Y, Wickramasinghe V K, Zimcik D G. A novel smart spring concept for helicopter blade vibration and noise suppression[J]. Materials Science Forum, 2005,475-479(3):2095-2098.

[6] 段昕智,徐艳,李建中.近断层地震脉冲效应对大跨度桥梁地震响应的影响[J].石家庄铁道大学学报(自然科学版),2011,24(3):1-6，15.

[7] Wickramasinghe V K, Chen Y, Zimzik D G. Experimental evaluation vibration of the smart spring impedance control approach for adaptive vibration suppression[J]. Journal of Intelligent Material Systems and Structures, 2008,19(2):171-179.

[8] 李敬松,冯新,周晶.近断层地震作用下悬跨海底管线响应分析[J].水利与建筑工程学报,2015,13(4):224-230.

[9] 田乐，蔡金龙，高旭辉.爆破振动在层状岩体中的衰减特性试验研究[J].华北水利水电大学学报(自然科学版)，2016,37(5):82-87.

[10] 于翔.地下建筑结构应充分考虑抗震问题—1995年大阪神地震破坏的启示[J].工程抗震,2002(4):17-20.

[11] Lysmer J, Kuhlemeyer R L. Finite dynamic model for infinite media[J]. Journal Engineering Methods, 1969,95(EM4):859-877.

[12] 费康,张建伟.Abaqus在岩土工程中的应用[M].北京：中国水利水电出版社,2009.

[13] 周晨光.高土石坝地震波动输入机制研究[D].大连：大连理工大学,2009.

[14] 黄胜.高烈度地震下隧道破坏机制及抗震研究[D].武汉：中国科学院研究生院(武汉岩土力学研究所)，2010.

[15] 柴华友,吴慧明,张电吉，等.弹性介质中的表面波理论及其在岩土工程中应用[M].北京：科学出版社,2008.

[16] 卓卫东,高智能,谷音.P-SV波斜入射时有阻尼成层介质自由波场的一维化时域算法[J].水利与建筑工程学报,2016,14(6):18-24，34.

[17] 王润富,陈国荣.弹性力学及有限单元法[M].北京：高等教育出版社,2007.

[18] 程纬.地震加速度反应谱拟合的直接法研究[J].工程力学,2000,17(1):83-87.

[19] 黄仕彪,张振亚,贺广零.人造地震动反应谱的非线性拟合[J].地震工程与工程振动,2012,32(3):23-27.