基于双旋迫击炮弹平台的改进型Sage-Husa自适应滤波滚转角测量算法

王佳伟， 祁克玉， 杨恺华， 梁轲， 闫杰

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.西安机电信息技术研究所 机电动态控制重点实验室, 陕西 西安 710065)

0 引言

基于中大口径迫击炮弹应用平台，采用惯性器件/卫星定位来组合测量弹体姿态和弹道参数，可将修正引信与弹体通过解耦部件连接、形成反向相对旋转状态，构成双旋受控迫击炮弹。在气动力作用下，修正引信头部的两对翼面分别产生滚转力矩和修正弹道所需控制力，这是目前国际上二维弹道修正引信技术中最具代表性的总体设计方案[1-3]。修正引信的实时滚转角直接影响修正方向，是弹道控制模块的重要输入信息，其准确测量是二维弹道修正技术有待解决的关键技术。

陀螺/卫星定位组合测量滚转角最早于1995年由Lucia提出[4]，近年来不少文献进行了进一步阐述：Park等[5]和Lee等[6]继承并改良了Lucia的算法，但却是在修正引信转速不大于3 r/s的微旋状态且恒定不变假设条件下提出的，与实际弹道中修正引信从起控至修正末段高达每秒数十转的转速跨度不符；Maley[7]提出了将扩展卡尔曼滤波(EKF)与磁传感器辅助测量算法相结合的方法，并从理论仿真层面进行了验证，但目前尚未有进一步的实验室硬件测试验证结果；文献[8]中所涉及的传统EKF滚转角测量算法对于真实弹道环境下较大转速变化范围的滚转角测量具有显著效果，但对于弹道末段弹丸章动所引发的陀螺径向两轴测量误差却无法消除，从而严重影响了滚转角测量精度。

Sage-Husa自适应卡尔曼滤波(SHAKF)可以在线估计量测噪声并具有较好的稳定性[9]，只是每次滤波都需要预估系统噪声，增加了迭代滤波的复杂度[10]。考虑到轴向陀螺测量修正引信转速的精度较高、可以作为补偿系统噪声的先验知识，本文提出了一种基于双旋迫击炮弹平台的改进型SHAKF滚转角测量算法，既能够提高滤波实时性，又能够大幅度降低量测噪声对滚转角测量精度的影响。

1 基本原理

1.1 陀螺/卫星定位组合算法

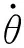
遗憾的是，该方法仅局限于不大于3 r/s微旋恒定转速条件下的滚转角测量，基于理论解析得到的滚转角又极易受到量测噪声影响，因此需要设计一种针对转速较大范围变化情况的自适应滤波算法。

1.2 简化SHAKF算法

设线性离散系统的数学模型为

X(k)=Φ(k,k-1)X(k-1)+Γ(k,k-1)W(k-1)，

(1)

Z(k)=H(k)X(k)+V(k)，

(2)

式中：X(k)为系统状态向量；Z(k)为系统观测向量；Φ(k,k-1)为系统状态转移矩阵；Γ(k,k-1)为系统噪声矩阵；H(k)为系统量测矩阵；W(k)和V(k)分别为系统噪声向量和量测噪声向量；k表示第k次滤波迭代。

简化SHAKF算法[12]为

(k)=Φ(k,k-1)(k-1)+K(k)V(k)，

(3)

V(k)=Z(k)-H(k)(k,k-1)，

(4)

K(k)=P(k,k-1)HT(k)·
[H(k)P(k,k-1)HT(k)+R(k)]-1，

(5)

P(k,k-1)=Φ(k,k-1)P(k-1)ΦT(k,k-1)+
Γ(k,k-1)Q(k)ΓT(k,k-1),

(6)

P(k)=[I-K(k)H(k)]P(k,k-1)[I-
K(k)H(k)]T+K(k)R(k-1)KT(k),

(7)

R(k)=(1-dk)R(k-1)+
dk{[I-H(k)K(k-1)]V(k)·
VT(k)[I-H(k)K(k-1)]T+
H(k)P(k-1)HT(k)},

(8)

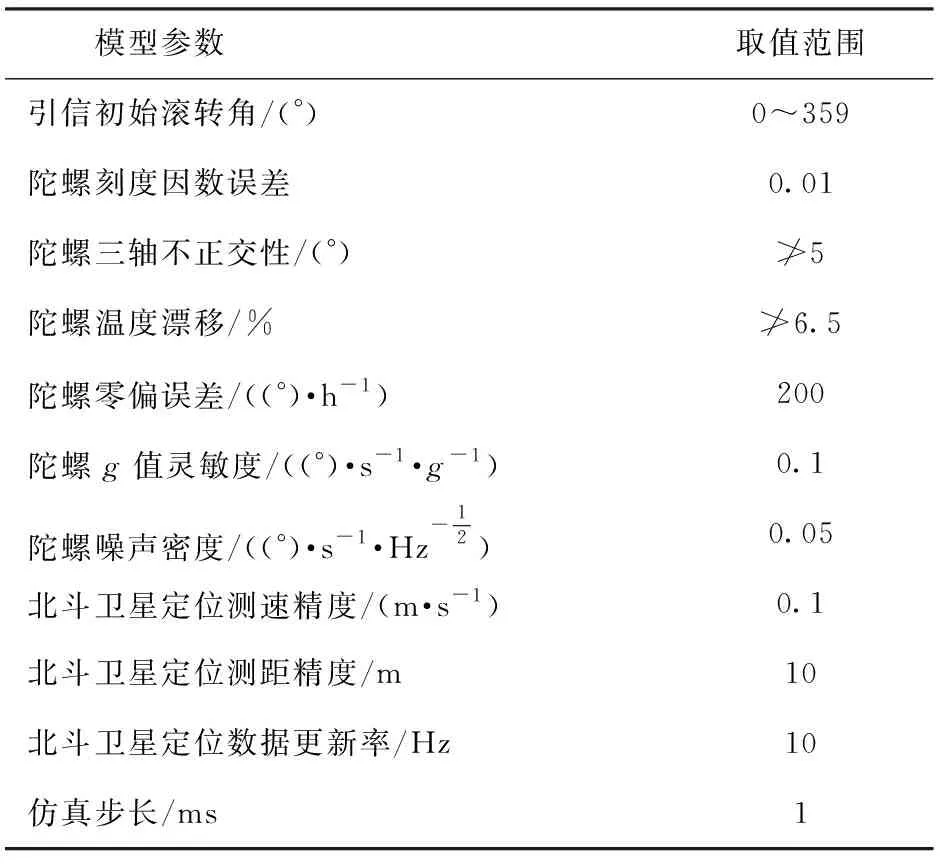
式中：dk=(1-b)/(1-bk+1)，0

2 改进型SHAKF算法

改进型SHAKF算法具体步骤如下：

1)X(k)、Z(k)、Φ(k,k-1)和H(k)参照文献[8]，Γ(k,k-1)改写为

(9)

2)滤波迭代中增加转速判据：根据(3)式～(8)式的滤波流程，当进行到第k次滤波时，针对计算得到的量测噪声进行滤波状态异常判断，异常判据为

vT(k)v(k)>δtr(E[v(k)vT(k)]),

(10)

式中：v(k)为新息序列；δ为储备系数，取值范围δ>1；tr表示矩阵的迹；E为求矩阵期望。若(10)式成立则说明实际误差将超过理论预估的δ倍，即滤波发散。由(10)式可以推导得到滤波异常判据的表达式如下：

vT(k)v(k)>δ[H(k)P(k,k-1)HT(k)+R(k)].

(11)

由于(11)式中P(k,k-1)包含转速补偿信息，此滤波异常判据体现了当前滤波过程中对新旧转速信息的利用程度：δ=1为最严格滤波异常判据，本文仿真验证选取范围为3≤δ≤5. 若(11)式成立，则认为实际余项与原假设不相容，此时通过(8)式计算R(k)以代替R(k-1)；反之，若(11)式不成立，则省去(8)式的计算、继续使用R(k-1)。

3)重复步骤1、步骤2，完成改进型SHAKF迭代算法。

3 仿真验证

3.1 仿真条件

下面利用双旋迫击炮弹模型对改进型SHAKF滚转角测量算法进行仿真验证。根据文献[8]仿真条件可知：射角采用最大射程角，弹丸初速为名义初速，在炮兵标准气象条件下弹丸全弹道保持稳定飞行。迫击炮弹尾翼产生的导转力矩和动压变化使得弹丸转速呈倒U型变化趋势且保持低速右旋(由弹尾向弹头方向看)；修正引信头部安装了与弹丸尾翼反向的导转翼面，在反向导转力矩作用下在全弹道内与弹丸旋转方向相反且转速较高，在修正阶段转速在15～25 r/s之间波动。全弹道范围弹丸和修正引信无控飞行的转速变化曲线如图2所示。

表1给出了应用于仿真验证的各主要测量参数。

3.2 对比验证

在3.1节所述仿真条件下，分别采用EKF滚转角测量算法与本文提出的改进型SHAKF测量算法进行比较，得到全弹道滚转角测量误差曲线如图3所示。

表1 测量模型参数

从图3可见：采用改进型SHAKF算法的收敛速度虽然与原EKF测量算法并无太大差别，但是其滚转角测量误差却显著降低：对滤波收敛后的滚转角测量误差进行统计，传统EKF算法的滚转角测量误差均值为2.86°，标准差为1.67°；而采用SHAKF算法的测量误差均值为0.26°，标准差为0.35°.

图4所示为滚转角测量误差对比的局部放大图。由图4可见，除去弹道15～40 s区间外，采用新算法的滚转角测量误差在升弧段和降弧段都远低于原EKF算法的结果，但都存在一个明显的趋势项。究其原因，是由于其各自所对应的转速与弹道中段相比较高，单位时间内修正引信滚转角增量也过大，同时其间的弹丸章动也带来更大的量测误差，这些都会导致预测协方差和滤波器的增益不能随新息同步改变，从而失去对突变状态变量的跟踪能力，使估计误差略有增加。以图2为例，修正引信的转速在弹道升弧段和降弧段都超过了18 r/s，这意味着仅在一个滤波步长周期内预估状态变量的增量就达到6.5°. 在仿真层面，通过提高SHAKF算法的滤波频率，或者减小滤波判据因子δ以提高滤波条件，二者都可以实现更高的滚转角测量精度，但不可避免地会降低滤波实时性并在硬件实现过程中大大增加微处理器的运算处理负担。对比采用原EKF算法的滚转角测量误差，改进型SHAKF算法对修正引信滚转角的估计效果是令人满意的，考虑到目前的解算误差满足修正系统精度要求，可暂不改变仿真步长。

4 实验验证

下面以高精度微机电系统传感器三轴转台作为硬件实验验证平台，验证改进型SHAKF滚转角测量算法。三轴转台如图5所示，滚转角测量硬件电路如图6所示。

为了模拟验证外弹道环境下修正引信的滚转角测量精度，通过设置三轴转台的俯仰和方位控制单元来模拟弹丸的俯仰、偏航姿态，设置滚转控制单元，将滚转速率由30 r/s均匀减小至1 r/s，以模拟弹丸的时变转速。固连在滚转轴上的滚转角测量硬件模块会采集并存储陀螺输出信号，最后将采用改进型SHAKF滚转角测量算法计算出的实时滚转角与理论值进行对比，并分析解算误差。三轴转台滚转角速率输出以及对应角速率条件下的滚转角解算误差曲线如图7所示。

由图7中可以看到：在修正引信转速自30 r/s至1 r/s范围的动态变化过程中，除了滤波迭代初期的震荡之外，仅有的滚转角解算失准皆出现在转速状态突变所对应的时刻(其收敛过程都不会超过200 ms)；改进型SHAKF滚转角测量算法始终能够保持较高的测量精度，且解算绝对误差不超过4.2°，由此可见该算法完全能够实现时变转速条件下的滚转角准确测量，并具有比传统EKF算法更高的测量精度和自适应性。

5 结论

本文针对传统EKF测量算法在弹道末段无法消除径向安装陀螺测量噪声导致滚转角测量误差偏大问题，利用轴向陀螺的实测转速作为系统噪声补偿，提出了一种基于双旋迫击炮弹平台的改进型SHAKF滚转角测量算法。所得主要结论如下：

1)通过与传统EKF算法进行仿真比对验证，结果表明：在相同仿真条件下，采用新算法的滚转角测量误差显著降低，同时其滤波器的自适应性对于弹道升弧段和降弧段滚转角新息改变的跟踪能力也远远优于EKF算法，滚转角测量误差均值为0.26°，标准差为0.35°.

2)以高精度三轴转台作为硬件实验验证平台，模拟验证外弹道环境下修正引信的滚转角测量精度，结果表明：改进型SHAKF滚转角测量算法始终能够保持较高的测量精度，且解算绝对误差不超过4.2°.

参考文献(References)

[1] Widmayer R S. Terminal trajectory correction capability for standard spinning projectiles[C]∥2nd International Symposium on Ballistics. Daytona, FL，US: International Ballistics Committee, 1976.

[2] Philippe W. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Chicago,IL, US: AIAA, 2009.

[3] Philippe W, Friedrich L, Denis B,et al. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Honolulu, HI, US: AIAA, 2008: 1-17.

[4] Lusia D J. Estimation of the local vertical state for a guided munition shell with an embedded GPS/micro-mechanical inertial navigation system[D]. Cambridge, MA, US: MIT, 1995: 33-51.

[5] Park H Y, Kim K J, Lee J G, et al. Roll angle estimation for smart munition[C]∥Proceedings of IFAC Symposium on Automatic Control in Aerospace. Toulouse, France: Pleiades Publishing，2007: 6-12.

[6] Lee H S, Kim K J, Park H Y. Roll estimation of a smart munition using a magnetometer based on an unscented Kalman filter[C]∥AIAA Guidance Navigation and Control Conference and Exhibit. Honolulu, HI, US: AIAA, 2008.

[7] Maley J M. Efficient attitude estimation for a spin-stabilized projectile[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 339-350.

[8] 王佳伟，史凯，徐国泰，等. 基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法[J]. 西北工业大学学报，2016，34(6): 938-944.

WANG Jia-wei, SHI Kai, XU Guo-tai, et al. Roll estimation of high rotation speed correction fuze based on extended Kalman filter[J]. Journal of Northwestern Polytechnical University, 2016, 34(6): 938-944.(in Chinese)

[9] Sage A P, Husa G W. Adaptive filtering with unknown prior statistics[C]∥Proceedings of the 10th Joint Automatic Control Conference. Boulder, CO, US: Elsevier，1969: 760-769.

[10] 张常云. 自适应滤波方法研究[J]. 航空学报，1998, 19(7): 96-99.

ZHANG Chang-yun. Approach to adaptive filtering algorithm[J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(7): 96-99. (in Chinese)

[11] 韩子鹏，赵子华，刘世平，等. 弹箭外弹道学[M]. 北京: 北京理工大学出版社，2008: 127-149.

HAN Zi-peng, ZHAO Zi-hua, LIU Shi-ping, et al. Exterior ballistics of projectiles and rockets[M]. Beijing: Beijing Institute of Technology Press, 2008: 127-149. (in Chinese)

[12] Narasimhappa M, Rangababu P, Sabat S L, et al. A modified Sage-Husa adaptive Kalman filter for denoising fiber optic gyroscope signal[C]∥Proceedings of 2012 Annual IEEE. Kochi, India: IEEE Computer Society，2012: 1266-1271.