基于双层规划的市郊轨道交通多交路快慢车开行方案优化研究
2018-06-29汤莲花徐行方
汤莲花,徐行方
(同济大学 道路与交通工程教育部重点实验室,上海201804)
0 引 言
与市内线路相比,市郊线路的客流主要以通勤出行为主,其时空分布表现出更明显的不均衡性,因此一些线路尝试采用新的运行模式.例如北京地铁6号线,上海地铁16号线采用了快慢车模式;南京地铁1号线,广州地铁2号线等多线路采用了大小交路模式.新的运行模式虽然取得一定的效果,但也带来了新的问题:大小交路模式虽然提高了小交路区段的运力水平,但延长了大交路列车乘客候车时间;而快慢车模式虽可减少长距离出行乘客旅行时间,但对于断面客流较大区段容易造成运能紧张,部分车站乘客候车时间延长.因此,为了同时解决市郊线路供需不匹配与长距离出行乘客旅行时间较长的问题,可以研究市郊线路多交路和快慢车结合的运营方案.
在国内外相关研究中,列车开行方案作为城市轨道交通运营组织的基础受到了广泛的重视.国外学者Furth P.G.[1]以列车满载率作为约束对不同交路列车的开行对数进行优化,但没有考虑乘客出行成本及企业运营成本;Site P.D.[2]以乘客出行成本和企业运营成本最小化为目标,建立列车开行对数、开行频率及发车间隔的优化模型,但没有考虑乘客换乘的等待时间;SuhWonho[3]针对首尔地铁5号线,通过仿真对比分析了快慢车模式与传统的站站停模式下各运营指标的优劣,但未考虑多交路问题;Nesheli M.M.[4]考虑同步换乘乘客的数量及出行时间,研究了不同调度策略(跳停、小交路等)下公交同步换乘问题,但只考虑了换乘的同步性,未考虑其他乘客的等待时间及公交运营的成本;Ulusoy Y.Y.[5]将大小交路和快车服务应用在公共交通网络中,建立了可同时优化乘客和企业成本的模型,但是在假设和实例中均提出预先确定小交路折返站位置.同时,国内学者在大小交路和快慢车开行方案的研究中,通常是预先固定小交路列车的折返站位置[6],或在讨论大小交路时预先固定列车停站方案[7]、在讨论快慢车时预先确定列车交路计划[8].
因此,本文将针对市郊线路客流量空间分布不均衡的特点,以快慢车结合多交路的列车开行方案为研究对象,以乘客的广义出行费用和企业的运营成本为目标函数,对小交路列车的折返站、快车停站方案,以及不同类型列车的开行频率进行优化.
1 问题描述
市郊线路多交路和快慢车结合的开行方案一般形式如图1所示[9],既缩短长距离出行乘客的旅行时间,又满足断面客流量较大区间的客流集散需求.因此,本文将讨论开行3种列车(用k表示列车类别),并以小交路慢车折返站、大交路快车停站方案,以及3种列车的开行频率作为决策变量,模型的基本假设为:

图1 快慢车和多交路结合运营示意图Fig.1 A typical train plan with multi-routing and express-local modes
假设1从规划的角度考虑,线路中的每个车站均具有修建折返线的条件.
假设2大交路的设置对小交路折返站折返时间无影响,各站折返时间相同;同时,大交路快车在小交路折返站必须停车.
假设3乘客出行最多只进行1次换乘.快换慢时,在遇到的最后1个快车站换乘;慢换快时,在遇到的第1个快车站换乘;乘客不会在大、小交路慢车之间进行换乘.
2 乘客广义出行费用分析
2.1 一般出行费用分析
(1)候车时间.
在发车间隔较小的城市轨道交通车站,客流到达服从均匀分布,其平均候车时间等于发车间隔时间的1/2.因此,乘客乘坐第k类别列车的候车时间为
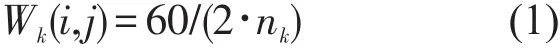
式中:nk为k类别列车高峰小时的开行对数(对/h).
本文考虑单一线路列车的开行方案,当乘客在不同种类列车之间换乘时,一般为同站台换乘,因此忽略换乘走行距离,换乘时间近似为旅客在换乘车站等待后续列车的候车时间.
(2)乘车时间.
包括区间运行时间与沿途停站时间之和,则从车站i到车站j的客流f(i,j)中选择乘坐k类别列车的客流f(i,j,k)的乘车时间为
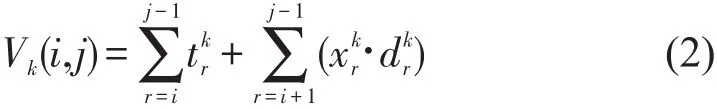
式中:trk为k类别列车在区间(r,r+1)的运行时间(min);dkr为k类别列车在车站r的停站时间(min);xrk为k类别列车在车站r停站的0-1变量,停站为1,通过为0.
(3)拥挤费用.
指由于列车载客能力的限制,使得乘客感知到的不舒适度,主要受断面客流量的影响.其中,k类别列车在区间(r,r+1)的断面客流量为

式中:sk、ek分别为k类别列车运行的起点和终到站.
则客流f(i,j,k)感知到的拥挤费用为
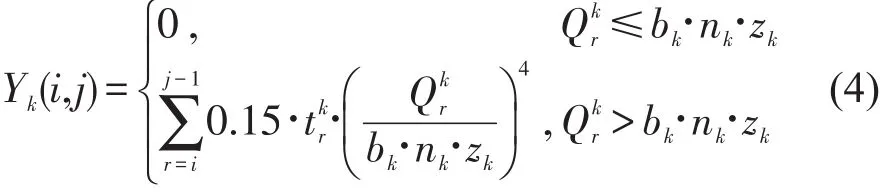
式中:bk、zk、nk为k类别列车的编组、定员、开行对数;0.15和4是拥挤费用的无量纲经验参数[9-10].
进一步将以上各项乘客出行的广义费用转化为货币支出,则客流f(i,j)的个体乘客选择k类别列车的广义出行费用为

式中:β为单位时间价值(元/min).
2.2 考虑乘客出行起讫点的乘客出行费用
由于小交路折返站和快车停站方案的未知性,对于不同出行起讫点的乘客而言,可选择的列车种类是不同的,这就加大了出行费用计算的复杂性,基于此提出一种考虑乘客出行起讫点的出行费用计算方法.首先,根据小交路慢车的折返站S1、S2将线路分为3个区段;然后,将不同出行起讫点的客流分类,如图2所示.不同分类乘客可选择的列车有以下几种情况.
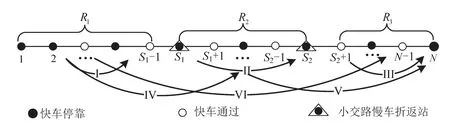
图2 基于乘客出行起讫点的客流分类Fig.2 Classification of passenger flow based on passengers’starting and ending points
情况1出行起讫点均在区段R1或R3,或者出行起点在R1、讫点在R3.此时乘客可选择的列车有大交路快车或大交路慢车,如图2中I、III、VI.
情况2出行起讫点均在区段R2,此时乘客可选择的列车有大交路慢车、大交路快车和小交路慢车,如图2中II.
情况3出行起点在R1,讫点在R2;或出行起点在R2,讫点在R3.此时乘客可根据情况在大、小交路之间进行换乘,如图2中IV、V.
对于上述情况,根据i,j是否为快车停靠站,可继续分为:①慢车站—快车站,②快车站—慢车站,③快车站—快车站,④慢车站—慢车站.因此,对于每一种情况,要对乘客可选择的路径和各路径对应的广义出行费用分别分析.
3 模型构建及算法设计
3.1 上层规划
在建立上层规划模型前,先分析企业的运营成本.
(1)车辆走行公里成本.

式中:αL表示车辆每公里走行成本;Lk为k类别列车的走行距离(km).
(2)车辆购置成本.
考虑到备用列车,列车购置数量取运用列车数量的1.2倍,即
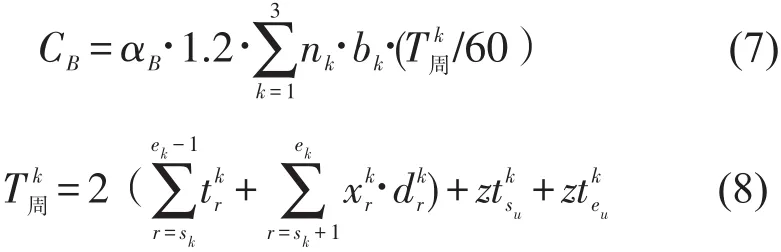
式中:T周k为第k类别列车的周转时间(min);ztksk、ztkek分别为k类别列车在两端折返站的折返作业时间;αB表示车辆的单位购置成本.
(3)列车停站成本.

式中:αT表示列车停站1次的成本.
在此基础上,建立上层规划模型为

式中:tmax、I0分别为乘客所能忍受的最大发车间隔和区间的最小追踪间隔;ηmin、ηmax分别为列车最小、最大满载率.
式(10)表示企业追求运营成本最小化;式(11)为列车停站约束,表示大交路快车在运行途中至少停1站,同时在小交路慢车运行区段的首末车站必须停车;式(12)为小交交路慢车运行区段的距离约束,表示小交路列车的运行距离不能过短和过长(过短导致列车频繁折返,过长无法实现小交路优 势),当 车 站 数 大 于 25 时 ,Zmin=(1/4)∙N ,Zmax=(3/4)∙N , 当 车 站 数 小 于 25 时 ,Zmin=(1/3)∙N,Zmax=(3/4)∙N[11];式(13)为追踪间隔约束;式(14)为发车间隔不应小于折返站发车间隔时间;式(15)为满载率约束;式(16)为发车频率的整数约束,列车停站的0-1约束,小交路慢车起终点站约束.
3.2 下层模型
基于所有可供选择的路径中,乘客所选择路径的广义费用期望值要小于未被选择的路径,因此提出客流分配的随机用户均衡问题优化模型,该模型的解已被文献[12]证明满足Logit形式的客流分配随机平衡条件.

式中:A={aw|w=1,…,nw}为线路OD对集合;nw为OD对总数量;为 OD 对aw之间所有路径集合;naw为OD对aw所有路径数量;为路径上的客流量;f(aw)为OD对aw之间的客流量;为连接关系变量,当OD对a之间的路径w覆盖k类别列车的运行区间(i,j)时,为 1,否则为0.
式(17)表示所有客流的广义费用最小;式(18)表示OD对aw之间的客流被分配到不同的路径上;式(19)表示客流f(i,j,k)与各路径客流量的关系.
3.3 求解算法
本文采用混合优化算法—遗传—模拟退火算法求解双层规划模型,该算法既克服了遗传算法局部寻优能力不强,易早熟,不收敛等缺点,又吸收了模拟退火算法较强的局部搜索能力.具体算法步骤如图3所示.
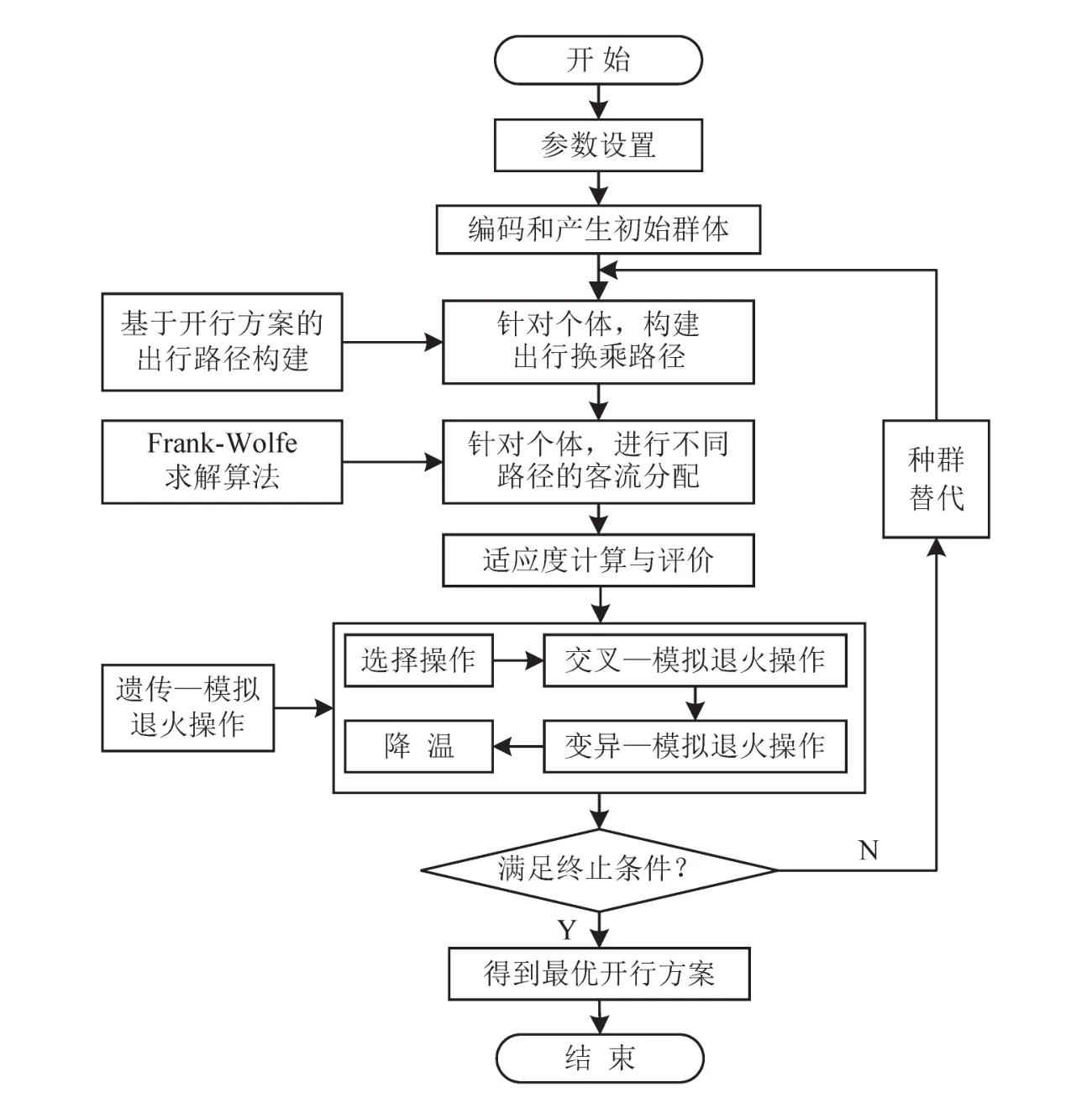
图3 双层规划模型求解算法流程图Fig.3 Flow chart of solving algorithm for bi-level programming model
4 实例验证
4.1 线路概况
以某市郊轨道交通线路为例,其站间距及运行时间如表1所示,其断面客流、沿线各车站单向上下车人数如图4所示.

表1 线路区间长度及运行时间Table 1 The length and running time of the interval on the line
从图4可以看出,线路最大断面客流量出现在第12和13个车站之间,客流分布呈现凸起状,根据断面客流不均衡系数公式为每个断面客流量,M为断面个数,pmax为最大断面客流量),可得该线路的断面客流不均衡系数为1.81,断面客流分布较为不均衡.与此同时,沿线各个车站乘降的客流量差别较大,有6个车站的上下车总人数占全线21个车站上下车总数的55%.可见,该市郊轨道交通线路的客流在空间上的分布不均衡程度较大,且在部分车站较为集中,具备尝试多交路快慢车开行方案的条件.
4.2 模型参数确定及求解
模型相关参数取值如表2所示.
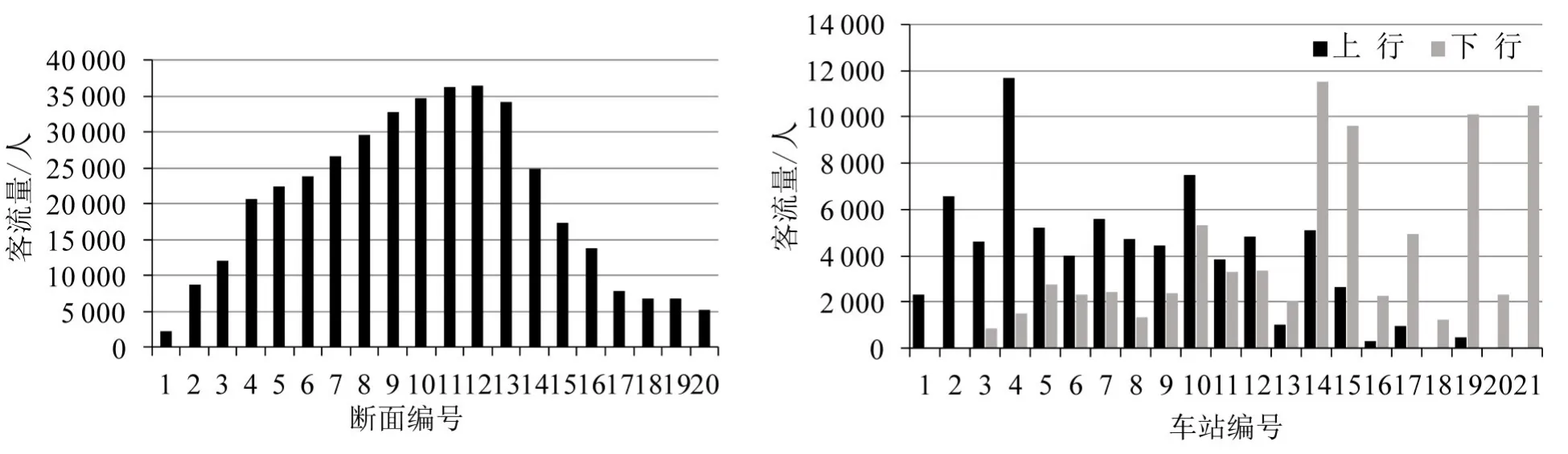
图4 某市郊轨道交通线路客流特征Fig.4 The characteristics of passenger flow in this suburban rail transit line

表2 模型相关参数取值Table 2 The values of the parameter in the model
结合前文提出的多交路快慢车开行方案双层规划模型,采用遗传—模拟退火算法.通过Matlab编程对模型进行求解,该算法的参数设置如下:初始种群大小n0为200,交叉概率pc为0.9,变异概率pm为0.01,初始温度T0为5 000,模拟退火算法的降温参数α为0.9,迭代的最大数量是1 000次.算法的迭代收敛和最优列车计划如图5和图6所示.
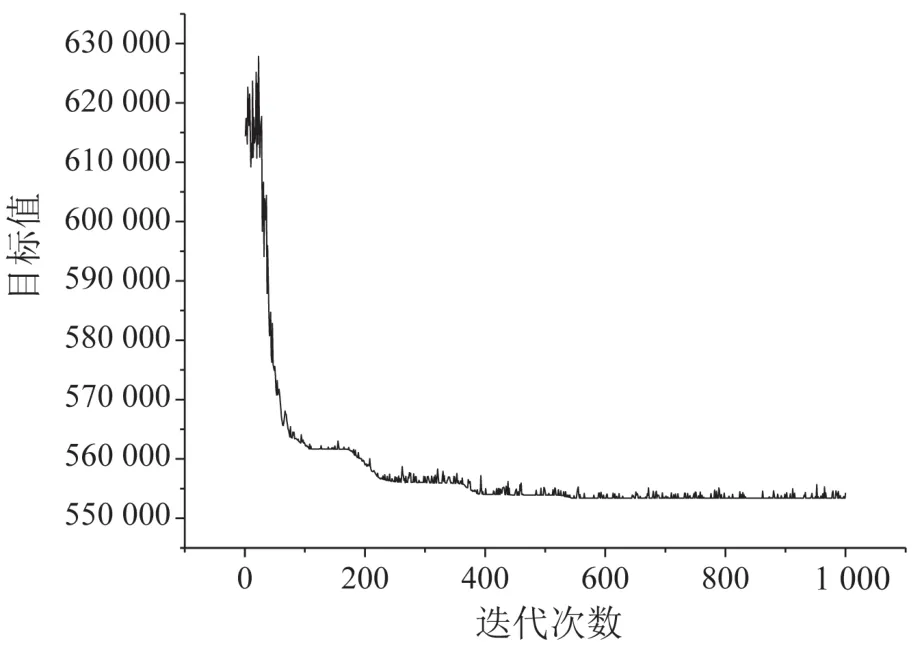
图5 算法的迭代收敛性Fig.5 The iteration convergence of the algorithm
从图5可以看出,当迭代次数小于200时,目标值变化明显,当超过400时,目标值趋于稳定.图6给出了不同开行模式的列车开行方案,可以看出本文建立的多交路快慢车开行方案,小交路慢车在第1~15个车站之间运行,大交路快车途中在9个车站停车,3种列车的发车频率分别为9,7,7.对比不同开行方案的评价指标如表3所示.

图6 不同开行模式的列车开行方案Fig.6 The train plan of different operation modes
从表3可以看到,尽管单一交路快慢车和大小交路快慢车模式下的候车时间比其他两种模式的都长,但是乘客的总旅行时间,企业的总运营成本均有了一定的优化.相较于目前城市轨道交通普遍采用的单一交路、站站停开行模式,本文建立的多交路快慢车模式下乘客的总旅行时间减少2 000 min,减少了2.25%;企业的总运营成本减少913万元,减少了9.25%,充分说明了多交路快慢车开行模式的优势.

表3 不同开行方案的评价指标Table 3 The evaluation index of different train plans
4.3 客流灵敏度分析
为进一步说明本文建立的多交路快慢车开行方案适用的客流情形,下面对客流进行灵敏度分析.令δ、ε分别表示快车停靠站下车客流量所占比重和小交路区段覆盖的OD客流量所占比重,将两者客流量分别调整至原有客流的ω=0.5、1.0、2.0、3.0倍,对应的δ为 58.97%、74.19%、85.18%、89.61%,对应的ε为81.78%、89.90%、94.72%、98.18%,则列车开行对数及节省的总运营成本随δ、ε的变化趋势如图7所示.

图7 δ、ε对开行对数和总运营成本的影响Fig.7 The effect ofδandεon train numbers and the operation costs
可得以下结论:
①当ω为0.5(减少至原客流量的1/2)时,最佳的运行模式为站站停和单一交路,表明快慢车、大小交路模式虽然能够降低乘客的出行费用和企业的运营成本,但需要一定的客流特征.
②随着δ、ε的增大,快慢车和大小交路模式节省的总运营成本呈增长趋势,表明客流在部分车站越集中、断面客流不均衡程度越大时,实行快慢车、大小交路模式越有利.开行频率,小交路列车的折返站位置及快车的停站方案.最后通过实例分析,不仅验证了模型和算法的有效性,也对比得出了在具有特殊客流特征的线路,多交路快慢车相结合的开行方案对于乘客和企业而言均是有利的.
5 结论
针对市郊客流时空分布的不均及不同车站乘降人数相差较大,本文将双层规划模型应用于建立市郊线路多交路快慢车开行方案,并设计了遗传—模拟退火算法进行求解,以获得不同列车的
[1]FURTH P G.Shortturning on transitroutes[J].Transportation Research Record,1987(1108):42-52.
[2]SITE P D,FILIPPI F.Service optimization for bus corridors with short-turn strategies and variable vehicle size[J].Transportation Research PartA Policy &Practice,1998,32(1):19-38.
[3]SUH W,CHON K S,RHEE S M.Effect of skip-stop policy on a korean subway system[J].Transportation Research Record Journal of the Transportation Research Board,2002,1793(1):33-39.
[4]NESHELI M M,CEDER A,LIU T.A robust,tacticbased,real-time framework for public-transport transfersynchronization[J].Transportation Research Part C,2015,60(11):105-123.
[5]ULUSOY Y Y,CHIEN I J,WEI C H.Optimal all-stop,short-turn, and express transit services under heterogeneous demand[J]. Transportation Research Record Journal of the Transportation Research Board,2010,2197(-1):8-18.
[6]王媛媛,倪少权.城市轨道交通大小交路模式列车开行方案的优化[J].铁道学报,2013,35(7):1-8.[WANG Y Y,NI S Q.Optimization of train schedules of full-length&short-turn operation modes in urban rail transit[J].Journal of the China Railway Society,2013,35(7):1-8.]
[7]邓连波,曾强,等.基于弹性需求的城市轨道交通列车开行方案研究[J].铁道学报,2012,34(12):16-25.[DENG L B,ZENG Q,et al.Research on train plan of urban rail transit with elastic demand[J].Journal of the China Railway Society,2012,34(12):16-25.]
[8]许得杰,毛保华,雷莲桂,等.城市轨道交通大小交路列车开行方案优化研究[J].交通运输系统工程与信息,2017,17(1):120-126.[XU D J,MAO B H,LEI L G,et al.Optimization for train plan of full-length and short-turn routing in urban rail transit[J].Journal of Transportation Systems Engineering and Information Technology,2017,17(1):120-126.]
[9]毛保华,刘明君,黄荣,等.轨道交通网络化运营组织理论与关键技术[M].北京:科学出版社,2011.[MAO B H,LIU M J,HUANG R,et al.Operational theories and key technologies of rail transit networks[M].Beijing:Science Press,2011.]
[10]DENG L B,ZENG Q,GAO W,et al.Optimizing train plan for urban rail transit with multi-routing mode[J].Journal of Modern Transportation,2011,19(4):234-239.
[11]魏国静.城市轨道交通线路列车长短交路设置方法研究[D].北京:北京交通大学,2013.[WEI G J.Nested train routing setting method of urban rail transit line[D].Beijing:Beijing Jiaotong University,2013.]
[12]四兵锋,毛保华,刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法[J].铁道学报,2007,29(6):12-18.[SI B F,MAO B H,LIU Z L.Passenger flow assignment model and algorithm for urban railway traffic network under the condition of seamless transfer[J].Journal of the China Railway Society,2007,29(6):12-18.]
