基于梯度提升决策树的高速公路交织区汇入位置模型

李 根，孙 璐*,2

(1.东南大学交通学院，南京210096；2.美国天主教大学土木工程系，华盛顿20064，美国)

0 引言

近年来，很多研究[1-4]都认为交织区汇入行为是引发瓶颈路段拥堵的原因之一，交织区频繁的不合理汇入行为会引发交通拥堵乃至主线交通流的失效.因此，对于高速公路交织区匝道车辆的汇入行为进行准确地建模显得非常重要.汇入位置是高速公路匝道汇入行为中最重要的行为之一.准确地建立汇入位置模型、预测匝道车辆的汇入位置，对于提高微观交通仿真模型的准确性、评价匝道的服务水平、设计匝道的长度及交通管理措施的提出都有着十分重要的意义.

通过录像采集数据，Polus等[5]分析了4条加速车道汇入位置的特点.Ahammed等[6]通过对加拿大的多条加速车道的录像分析，建立汇入位置与加速车道长度、交通量之间的关系.然而这些模型都是基于宏观历史数据对汇入位置的均值进行估计的模型，并没有考虑具体的交通流状态对汇入位置的影响，也不能用于个体车辆汇入位置的预测.

Chu等[7]假设车辆的汇入位置服从正态分布，分析了交通状态，加速车道长度等对于汇入位置的均值和方差的影响，建立了位置的均值与方差和解释变量之间的线性模型.Weng等[8]假设汇入位置服从对数正态分布，建立了汇入位置与交通流密度、速度之间的模型.这类模型能够较好地体现汇入位置的随机性，但是也只能体现汇入位置的均值和方差与影响因素之间的线性关系，而驾驶行为是一个非常复杂的非线性过程，线性模型不能准确地反映影响因素对汇入位置的实际影响.

为了克服以上缺点，本文提出运用梯度提升决策树(GBDT)的方法对高速公路交织区车辆汇入位置进行建模并对模型进行训练和测试，试图通过数据挖掘的方法来深度挖掘车辆汇入位置与解释变量之间的隐性关系.本文还分析了车辆进入匝道时的初始横向位置对汇入位置的影响，证明了汇入行为是一个包括横向行为和纵向行为的二维行为.最终，本文将GBDT模型和Lognoraml模型进行了对比，并分析了各变量的重要性及对于汇入位置的影响.

1 梯度提升决策树(GBDT)介绍

Freiman[9]在1999年提出梯度提升决策树(Gradient Boosting Decision Tree,GBDT)算法.GBDT的基础是对决策树中的回归树的迭代优化.基于梯度提升(Gradient Boosting)迭代的思想，GBDT在每次迭代时通过最小化其损失函数，在减少残差的梯度方向新建立1棵弱决策树，最后将所有树的结论累加起来得到最终预测结果[10].

我们将驾驶员的汇入位置用y表示，影响驾驶员汇入位置的变量用x表示，N表示用于训练的样本数.GBDT建模过程如下.

(1)初始化学习器.

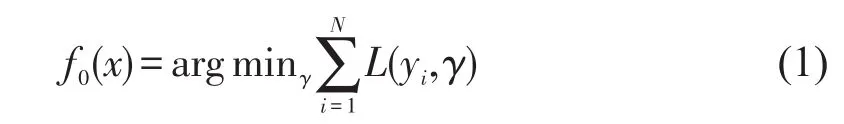
式中：γ为估计使损失函数极小化的常数值，它是只有1个根节点的树；L(yi,γ)为损失函数.

在GBDT模型中，对于回归问题采用的损失函数为均方误差损失函数(Square Error Loss).

(2)对于迭代轮数m=1,2,…,M，计算此时的负梯度为

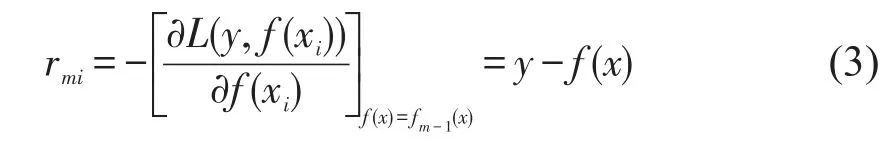
根据所有的样本及其负梯度方向(xi,rmi),i=1,2,…,N，得到1棵由J个叶子节点组成的决策树，其对应的叶子节点区域为Rmj,j=1,2,…,J，各个叶子节点的最佳残差拟合值为

本轮得到的学习器为

其中

(3)经过M轮迭代，得到最终的决策模型为

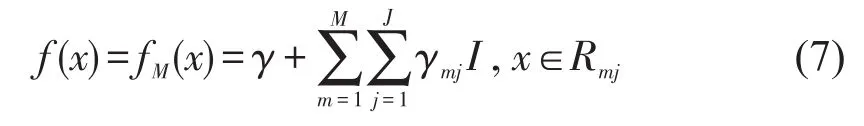
根据变量在迭代过程中被选为回归树的分裂变量的次数，以及其在分裂过程中对于模型精度的提高，可以得到每个变量的重要程度[10]为

2 数据介绍与变量分析

2.1 数据介绍

本文采用美国联邦公路局的NGSIM研究项目中所得到的车辆轨迹数据.我们选取其中的高速公路US101路段上采集的车辆轨迹数据，该路段全长640 m，包含了5条普通车道、1条进口匝道、1条出口匝道及2条匝道之间的集散车道，如图1所示.NGSIM提供的轨迹数据包括车辆的位置、速度、加速度、车型、车头时距等，时间精度为0.1 s/帧[11].该项目的数据是目前最为全面准确的高精度车辆轨迹大数据，被很多国家的很多研究人员用来进行微观交通流、宏观交通流、交通行为预测、交通仿真等方面的研究.

图1 US101线形与采集路段Fig.1 U.S.Highway 101 study corridor from NGSIM

本文研究的是高速公路交织区匝道车辆汇入位置，具体而言，就是车辆由辅助车道开始汇入主线时相对辅助车道起始位置(即匝道与主路标线交界处)的纵向距离，如图2所示.由于部分处于录像开始阶段和结束阶段的数据不能提供完整交通流状态，因此我们对数据进行了全面的检查和筛选，最终一共得到了366组数据

车辆汇入位置的分布及其基本统计量分别如图3和表1所示.可以看出，车辆汇入位置分布的最大峰值在35 m左右，呈现出非常明显的拖尾及多峰特性，汇入位置的均值为92.44 m，中位数为60.98 m，标准差为72.54 m，采用单一的分布模型难以描述其特性.

图2 汇入位置的定义Fig.2 Definition of merging position

图3 汇入位置的分布图Fig.3 Distribution of merging location

2.2 变量选取与分析

根据以往研究[5-8]的结果，影响车辆汇入位置的因素主要有主线相邻车道的交通流密度K、辅助车道交通流密度Km、汇入车辆在进入辅助车道时的初始速度V，以及汇入车辆与主线车流和辅助车道车流的速度差DV、DVm.然而汇入行为是典型的强制换道行为，而换道行为主要体现的是车辆在道路横向的行为，因此我们猜想匝道车辆的汇入位置与车辆进入辅助车道时的初始横向位置X也可能有一定的关系，因此本文将初始横向位置X也作为影响因素引入模型中.

表1 汇入位置分布的统计量Table 1 Basic statics of the distribution of merging location

汇入位置与各变量之间的散点关系如图4所示.汇入位置与选取的各变量之间的相关系数及其P值如表2所示.与我们猜想的一样，匝道车辆进入辅助车道时的初始横向位置X与汇入位置之间有较强的相关性.而辅助车道的车流密度与汇入位置之间的相关性则接近于0，其他参数与汇入位置之间也存在显著的相关性.

3 模型建立与结果

GBDT模型的表现由决策树数量M，单棵决策树叶子数J及学习效率R这3个参数决定.本文采用美国Salford公司开发的数据挖掘软件Salford Systems建立GBDT模型.根据以往的研究[9-10]经验并结合本文模型的样本数量，我们将J和R分别设定为6和0.01.Salford Systems软件可以根据目标函数自动确定决策树数量M，最终得到其最佳的决策树数量M为289.

本文还利用相同的数据建立了Lognormal模型并进行卫队，根据对变量系数的检验及其P值，K、Km及DVm这3个变量没有进入模型，得到的具体的模型为

式中：ε～N(0,0.56)为正态分布.

表3给出了2种模型的AIC，BIC和R2，可以看出，本文模型在3种精度指标上都有较大幅度的提高，说明本文提出的GBDT方法对于建立汇入位置模型是较为合适的.

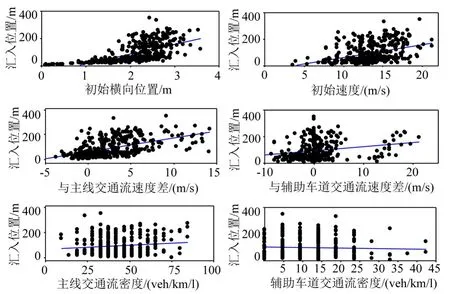
图4 汇入位置与各变量之间的散点关系图Fig.4 Relations between merging location and exploratory variables

表2 汇入位置与各变量之间的相关性系数Table 2 Correlation coefficients between merging location and exploratory variables

表3 GBDT与Lognormal模型对比Table 3 Comparison between GBDT model and Lognormal Model

4 变量分析

GBDT模型通过变量在迭代过程中被选为回归树的分裂变量次数，以及其在分裂过程中对于模型精度的提高来确定变量在模型中相对重要性，其重要性变量通过式(7)来计算，Salford System软件根据最后得到的决策树，给出了相对重要性，如图5所示.可以看出，影响匝道车辆汇入位置的最重要的变量是X，这与我们在前面的相关性分析是一致的.我们猜想，很多匝道车辆驾驶员在进入辅助车道之前已经通过对主线交通状态的观察确定汇入的策略，如果主线交通流状态较好或者驾驶员希望早汇入主线，驾驶员就通过调整车辆在车道的初始横向位置，贴近主线车道并择机汇入，因此当横向距离较小时，初始横向位置与汇入距离之间呈现较强的正相关性；如果主线交通流状态比较拥堵或者驾驶员希望晚点汇入主线车道，驾驶员可能通过调整车辆的初始横向位置，相对远离主线车道，并通过增加横向距离来提高对相邻车道的观察距离，因此，此时初始横向位置与汇入位置之间仍然呈现正相关性.

图6是解释变量对汇入位置的偏效应.可以看出每个变量对汇入位置的影响都有着较强的非线性关系.对于初始横向位置X，当X在[1,3]m的时候，汇入位置随着横向距离的增加而变远，呈现出较强的相关性.对于与主线车流速度差DV，当DV在[-1,8]m/s的时候，大致呈现汇入位置随着速度差的增加而变远的趋势；但在[4,6]m/s有所波动，说明GBDT模型能够深度挖掘汇入位置与变量之间的隐性关系.对于初始速度V，当V在[14.5,16.5]m/s的时候，汇入位置随着速度的增加而迅速变远，呈现出较强的相关性.

DVm、K和Km均没有进入Lognormal模型，然而在本文提出的GBDT模型，尽管其相对重要性较低，但是仍然对汇入位置有一定的影响，GBDT模型能够挖掘并发现其中的影响关系.从图6可以看出，DVm与汇入位置有非常明显的非线性关系，在速度差[-3,0]m/s上，汇入位置随着速度差绝对值的减少而变远；在[0,2.5]m/s上，汇入位置随着速度差的增加而由远变近；在[2.5,4]m/s上，汇入位置又随着速度差的增加而变远.对于主线交通流密度，当密度在[0,50]veh/km/l的时候，对于汇入位置几乎没有影响；然而在[50,70]veh/km/l，汇入位置随着主线交通流密度的增加而增加，说明当主线交通流密度较低的时候，车辆的汇入位置主要与驾驶员的个人驾驶行为有关，而当主线交通流密度较高时，交通流状态处于不稳定流或拥堵状态，由于驾驶员难以找到可以汇入的间隙而导致汇入位置变远.辅助车道交通流密度对于汇入位置的影响最小，只有当密度在[10,20]veh/km/l的时候，对于汇入位置有一定的影响.

图5 变量相对重要性Fig.5 Relative importance of variables

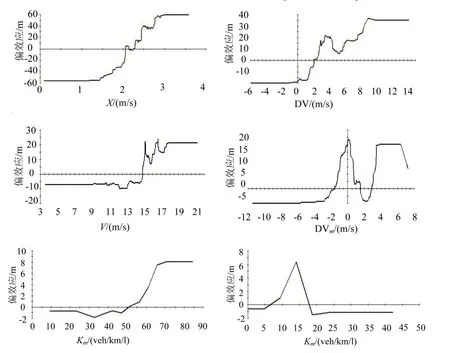
图6 各变量对预测结果的偏效应Fig.6 Partial effects of variables

5 结论

本文提取NGSIM数据库中高速公路US101的汇入车辆轨迹数据，建立了基于GBDT的高速公路交织区的匝道车辆汇入位置模型.汇入行为是一个典型的强制换道行为，是车辆在道路横向和纵向2个方向上的驾驶行为，因此我们分析了匝道车辆在进入辅助车道时的初始横向位置与汇入位置之间的关系.通过与Lognormal模型的对比，本文提出的GBDT模型大幅度提高了AIC，BIC和R2这3个指标.

所有采用的解释变量中，初始横向位置对于汇入位置模型的重要性最高，这说明汇入行为是一个在横向与纵向2个方向上的二维驾驶行为，两者之间有着重要的联系.本文还对解释变量的偏效应进行了分析，表明解释变量与汇入位置之间呈现较强的非线性关系，说明本文提出的GBDT模型不仅能够提供更准确的汇入距离预测值，还能够深度挖掘汇入位置与变量之间隐藏关系，能够提高微观交通仿真的准确性.

在后续研究中，将采集更多不同地点的数据对模型进行比较和验证，并进一步挖掘与分析引发各变量变化的原因，同时考虑将驾驶员的个体差异性加入到模型中，使模型的精度进一步的提高.

[1]HOU Y,EDARA P,SUN C.Modeling mandatory lane changing using bayes classifier and decision trees[J].IEEE Transactions on Intelligent Transportation Systems,2014,15(2)：647-655.

[2]CASSIDY M J,BERTINI R L.Some traffic features at freeway bottlenecks[J].Transportation Research Part B：Methodological,1999,33(1)：25-42.

[3]SARVI M,KUWAHARA M.Microsimulation of freeway ramp merging processes under congested traffic conditions[J]. IEEE Transactions on Intelligent Transportation Systems,2007,8(3)：470-479.

[4]PATIRE A D,CASSIDY M J.Lane changing patterns of bane and benefit：Observations of an uphill expressway[J].Transportation Research Part B,2012,15(4)：656-666.

[5]POLUS A, LIVNEH M. Comments on flow characteristics on acceleration lanes[J].Transportation Research Part A：General,1987,21(1)：39-46.

[6]AHAMMED M A,HASSAN Y,SAYED T A.Modeling driver behavior and safety on freeway merging areas[J].Journal of Transportation Engineering,2008,134(9)：370-377.

[7]CHU T D,MIWA T,MORIKAWA T.An analysis of merging maneuversaturban expressway merging sections[J].Procedia-Social and Behavioral Sciences,2014(138)：105-115.

[8]WENG J,MENG Q.Modeling speed-flow relationship and merging behavior in work zone merging areas[J].Transportation Research Part C： Emerging Technologies,2011,19(6)：985-996.

[9]FRIEDMAN JH.Stochasticgradientboosting[M].Elsevier Science Publishers B.V.,2002.

[10]FRIEDMAN J H,MEULMAN J J.Multiple additive regression trees with application in epidemiology[J].Statistics in Medicine,2003,22(9)：1365-1381.

[11]ALEXIADIS V,COLYAR J,HALKIAS J,et al.The next generation simulation program[J].Ite Journal,2004,74(8)：22-26.