基于换道决策机理的多车道元胞自动机模型

邓建华，冯焕焕

(苏州科技大学土木工程学院,江苏苏州215011)

0 引言

上世纪末Rickert等首先在NaSch模型中引入换道规则进行双车道模型扩展，提出了对称同向双车道元胞自动机(Symmetric Two-lane Cellular Automata,STCA)模型[1]；本世纪初，一些学者在此基础改进提出了3车道换道规则[2].目前，一般根据考虑影响换道决策因素的不同，把换道模型归纳为以下几类：考虑道路交通流密度、最小跟驰安全距离等车流内部状态变量的换道模型；考虑车道合并、分流点为外部约束因素的强制换道模型；响应鸣笛效应、制动刹车等简单车辆间信息交互的协作换道模型[3-5].可以看出上述每类模型在考虑影响换道驾驶行为因素方面往往相对单一和分散，部分局限了通用换道决策模型的提出与发展.

在对多车道换道决策机理进行详细分析的基础上，本文提出把影响驾驶员换道决策的因素分为外部因子与内部因子；以STCA模型换道规则为基础，改进其中与换道动机相关的车流内部状态变量因子表达式，提出了以内部因子为决策变量的换道动机生成函数，外部因子为约束条件的换道决策模型.

1 换道决策机理分析

车辆在行驶过程中产生换道动机是驾驶员通过视觉、听觉等途径对所处交通流内部前后相邻车辆运行状态信息感知和分析判断的结果.同向车流中，直接导致驾驶员产生换道动机的因素主要来自车流内部周边车辆与本车的行驶状态及空间关系.驾驶员对获知这些因素信息的处理将可能产生换道动机.常见导致产生换道动机的信息处理有：

(1)相对速度信息.处于同一车道的紧邻前车速度较小，本车驾驶员较长时间达不到心理期望速度.

(2)间隔距离信息.处于同一车道的紧邻前车制动使车辆间距缩短过快，本车驾驶员感知到存在与其发生追尾碰撞的危险.

只要其中一个信息符合就可能让驾驶员产生换道意愿即换道动机.当存在换道动机时，驾驶员需进一步根据车流内部以外的影响因子来确定换道决策目标方案的可行性，当换道外部可行性条件满足时则选择换道驾驶，否则车道保持.对于多车道元胞自动机模型来说需要架构合适换道决策模型以确定换道目标位置与速度.换道决策机理如图1所示.

换道可行性条件主要指车流内部因子以外的道路、交通管理、交通法规等外部影响决策的因素，如视距不良路线、坑洼路面、左侧超车规则、禁止变换车道标线等都可能对换道动机具有特定约束作用，影响换道驾驶行为最终可行性.

图1 换道决策机理Fig.1 Lane-changing decision mechanism

从图1看出：车流内部运行状态转换的决策变量是驱动产生换道动机的内部因子，换道可行性条件涵盖了约束换道目标决策的外部因子.

2 换道决策影响因子分析

2.1 内部因子

STCA模型换道规则核心表达式[1]为

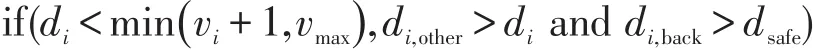
then：产生换道动机

else：车道保持

式中：di、di,other、di,back分别表示第i辆车与本车道紧邻前车的间距、相邻车道紧邻前车的间距与相邻车道紧邻后车的间距；dsafe表示模型中设定安全换道间距，dsafe=vmax.

(1)间隔距离因子.

对于3车道以上的多车道元胞空间，以车辆CA[i,j]为描述对象，重新定义间隔距离因子，具体定义如图2所示.

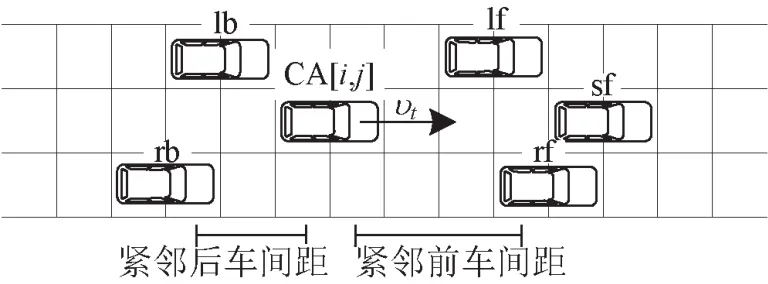
图2 CA[i,j]与紧邻前后车辆位置关系Fig.2 Position relations of theCA[i,j]and adjacent vehicles

设当前车辆CA[i,j]处于元胞空间纵向(车辆行驶方向)位置为xi，横向(车道位置)位置yj.其他紧邻前后车辆的纵向位置为xn(n=lf,sf,rf,lb,rb)，则

CA[i,j]紧邻前车间距为

CA[i,j]紧邻后车间距为

式中：li,veh为当前CA[i,j]车身长度；ln,veh为相应紧邻后车车身长度.

车辆CA[i,j]的驾驶员最容易根据紧邻车道的紧邻前后车辆与本车之间的位置状态进行间隔距离估计.元胞自动机模型运行从时刻t更新t+1时将获得5个影响换道决策的间隔距离因子：紧邻前车间距(左前距、直前距、右前距)分别表示为当前车辆车头与相应侧紧邻车道的紧邻前车车尾间的距离；紧邻后车间距(左后距、右后距)分别表示为当前车辆车尾与相应侧紧邻车道的紧邻后车车头间的距离.

STCA模型换道规则以当前车辆与紧邻前车期望间距，及与紧邻后车最小安全间隔作为换道判断规则，没考虑当前车辆与紧邻前车、紧邻后车的相对速度影响.

(2)相对速度因子.

车辆产生换道动机还与前后邻车的相对速度有关.设在t时刻，当前车辆速度为vi，紧邻前后车辆速度vn.

CA[i,j]前车相对速度为

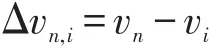
CA[i,j]后车相对速度为

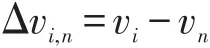
一般情况下，当(Δvn,iand Δvi,n)≥0时，才具有换道动机.

2.2 外部因子

主要指交通流自身内部运行状态变量因子以外的其他影响换道决策的因素，构成描述换道可行性的条件，对驾驶员最终换道决策起约束.

如前所述，路线路面条件、车道位置、交通标志标线等外部因子往往难以量化，模型中以外部因子p∈(0 ,1)来表示：当取p→0时，表示外部因子约束作用较大，促使驾驶员换道行为趋于保守；当取p→1时，表示外部因子约束作用降低，促使具有换道动机的驾驶员采取比较激进的换道驾驶行为.

3 改进的多车道元胞自动机换道决策模型

当前现有元胞自动机换道规则：di＜min(vi+1,vmax)表示车辆与本车道前方紧邻车辆之间隔距离不能满足期望的速度行驶，则可能产生换道动机.当vi+1略小于vmax时，该式成立则也可能导致产生换道动机，这与实际交通流中，当车流密度小、服务水平较高时，车辆能保持在低于vmax的较高期望行驶速度而不换道的情况不相符.

不同于双车道，多车道元胞空间存在左侧、右侧车道同时满足产生换道动机的情况，如何明确换道动机所指向的具体目标车道，目前常见处理方法通常由算法中条件语句固定的执行顺序或在算法中设置随机概率来确定指向换道目标，显然存在不合理性.

结合前述对换道决策机理与内外因子在换道决策过程中的作用分析，提出换道动机生成函数如下.

C1：then生成换道机动

式中：vi,hope为最大期望车速，模型运行时可以取vi,hope=0.85vi,max，可以减少车流平均速度较高时的随意变道行为.

式中：prf、plf分别定义为右、左换道动机的内部因子权值，为内部因子的函数.具体换道动机指向相应权值较大的一侧车道，不再由算法语句执行语句的顺序或设置随机概率来确定.

else：车道保持，无换道动机

上述生成函数中：动态间距[7]d′n,i(或d′i,n)(n=lf,sf,rf,lb,rb)改进为d′n,i=dn,i+max(vn,desired-gapsafety)，其中vn,desired改进为换道目标车道紧邻前车下一时刻最有可能的预测速度，gapsafety为最小安全车距.类似改进：d′d′为相应侧后rb,safe、lb,safe紧邻车辆n的安全动态间距，用于修正模型采用dsafe=vmax条件过于宽松的情况.改进的动态间距表达式可以描述驾驶员根据目标车道紧邻车辆间距和相对速度因子判断是否换道以外，还可能会预测目标车道紧邻前车下一步最可能的运行速度来确定换道动机的情况.

C1～C4构成了换道动机生成函数核心部分，表述了换道动机生成过程，包含4个判断：C1表示当前车辆i在本车道可能间距不能满足跟车的速度要求，具有换道意愿；C2表示当左侧、右侧车道同时满足产生换道动机的情况，则根据计算内部因子权值指向具体换道动机方向；C3和C4表示当单侧具有换道动机时，则生成相应侧的换道动机，否则无换道动机，车道保持.

上述模型能适用于实际交通环境条件下多车种组成带来的多种期望行驶速度和多种车身长度的情况；换道动机仅由交通流内部运行状态决定，不需人为设置一个作用于内部因子的随机换道概率[2].

当换道动机确立后，如车流处于无外部因子影响的理想状态，则驾驶员将根据换道动机采取换道操作；当存在外部因子约束换道动机时，如：换道目标车道路面损坏严重、车道分界标线为禁止变换车道线等外部因子严格约束换道动机，则可能使换道驾驶无法最终实施.因对外部因子的选取不是本文研究重点，如2.2节对外部因子p的定义，进行模型演化时，分别取p=0.2、0.4、0.6、0.8来模拟外部因子对换道行为约束作用强度.

4 改进的多车道元胞自动机模型运行分析

4.1 模型演化规则

在姜锐等[7]的一维改进舒适驾驶模型(Modified Comfortable Driving,MCD)基础上嵌入前述换道规则算法得到本文基于内外因子换道决策机理的多车道元胞自动机模型，其更新演化规则如下：

(1)首先确定慢化概率pdec.

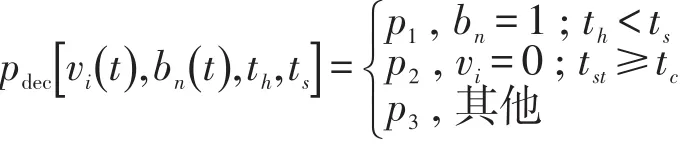
式中：th为车头时距，th=di/vi(t)；ts为安全时间间距，ts=min[vi(t),h]；h为刹车灯影响范围；bn=1(0)表示刹车灯亮(灭)，n=lf,sf,rf；tst为车辆停驶时长；tc为慢启动时间.

(2)加速.

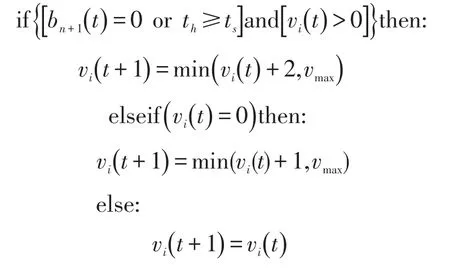
(3)减速.

(4)慢化.

(5)确定车辆运行工况wci(t +1)、加减速度adi(t+1)、刹车灯状态bi(t +1).

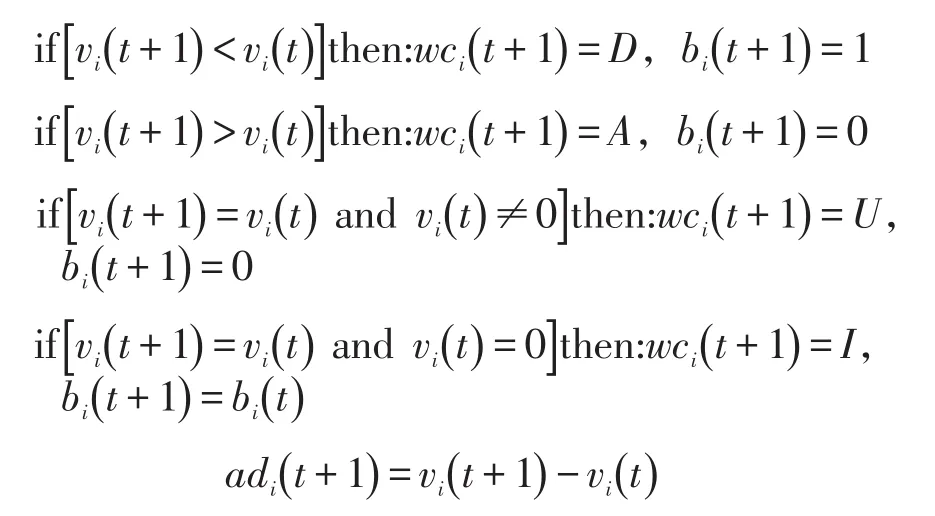
式中：wci(t +1)的枚举值；D为减速工况；A为加速工况；U为匀速工况；I为怠速工况.

(6)确定停驶时长tst.

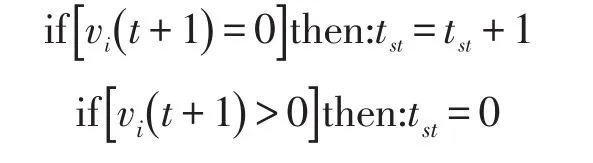
(7)调用本文提出的换道决策模型函数，进行换道决策，确定更新目标车道.

(8)车辆位置更新.

4.2 模型运行分析

模型运行参数：初始元胞空间设为12 000单位元胞，采用周期性边界.轻型车行驶最大车速为道路设计车速60 km/h=16.67 m/s，相当于1次更新30单位元胞长，即vmax=30；单位元胞长0.55 m，车身长6 m，占11个元胞单位，系统中其他车长与车速可进行相应换算；模型运行其他参数：p1=0.9，p2=0.5，p3=0.1，h=15，gapsafety=2，tc=15，

饱和度V/C值是表征交通流服务水平的重要指标之一.理论上，对于周期性边界元胞空间，随着输入系统车辆数增多，则饱和度增大，车辆间隔距离缩小并可能导致平均车速降低.按照V/C值每递增0.1向系统内输入相应的车辆数以表示内部因子的变化，同时选取4个p值表示外部因子的变化来进行模型模拟运行，每次内外因子参数组合运行100 000 s，考虑数据的稳定性，取尾端3 600 s输出数据进行统计分析.

4.2.1 平均换道次数分析

换道次数是换道决策成功的标志.不同运行参数环境下的3 600 s平均换道次数(次/s)统计结果如图3所示.

图3 不同内外因子条件下的平均换道次数Fig.3 Average lane-changing times in different conditions of internal and external factors

从图3可以看出：

(1)p=0.2时，表示外部因子约束作用较大，对全密度区间车流都起到较严格约束作用，p=0.2对应平均换道次数在全密度区间接近于零.

(2)p＞0.2时，平均换道次数在V/C=0.3附近开始迅速增加，然后在V/C=0.4处达到极大值，约为250～300次/s，除以系统内车辆数得车均换道约0.10～0.15次/s.随着V/C值进一步增加而呈现缓慢下降形态.p=0.8时，表示约束条件最宽松.

4.2.2 单车逐秒运行工况状态分析

从图3看出，当V/C≤0.2和V/C＞0.8时，4种p值所对应平均换道次数都接近于0，说明该服务水平范围内，外部因子对系统内车辆的运行状态影响极小.以下仅取交通流中任意单车在0.2＜V/C≤0.8时区间的4种典型工况运行状态数据进行统计，如图4所示.可以看出：

(1)当0.2＜V/C≤0.4时，不同p值对应平均换道次数显著增加，车辆保持匀速工况状态秒数减少，加速、减速工况状态增多.

(2)当0.4＜V/C≤0.8时，平均换道次数逐步降低.相同V/C值、不同p值对应平均换道次数不同，各种工况秒数也不同，总体上减速工况减少而怠速工况时长显著增加说明激进换道行为增加，且对车流干扰较大.匀速、加速工况时长进一步减少.

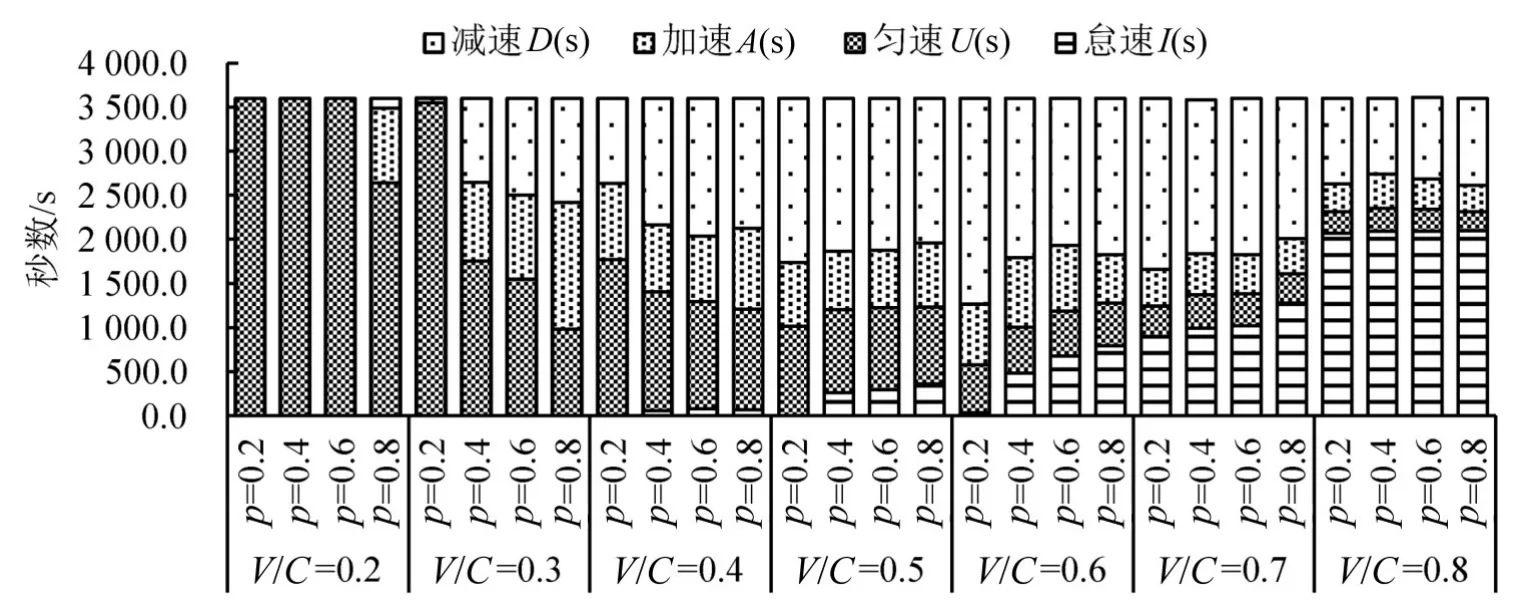
图4 单车逐秒工况分布Fig.4 The distribution of one vehicle’s working conditions each second

4.2.3 车流平均速度分析

对模型运行输出数据整理，如图5所示，并对不同V/C值和p值下的交通流平均速度进行分析.

(1)V/C＜0.2时，绝大多数车辆处于间距很大的非跟驰自由行驶状态，这种状态下的车辆一般不会产生换道动机，外部因子起不到约束作用.

图5 不同内外因子条件下的车流平均速度Fig.5 Average traffic flow velocity in different conditions of internal and external factors

(2)随着系统中车辆数增加，车流逐渐开始进入同步流状态.表示约束严格，V/C=0.3附近才开始进入同步流状态，说明在密度较小区间严格约束车辆变道行为有利于提高车流平均速度.进入同步流状态后，换道决策主要由p=0.2的严格约束作用控制，车速下降过程中波动较小.

(3)随着V/C增大进入同步流状态后，具有换道动机的车辆增多，p=0.4与p=0.6表示约束作用适中，有更多的换道动机被约束而跟驰前方慢车，使得车流速度下降速率很快，在V/C=0.4左右，速度降到最低.随着V/C进一步增大，由内部因子决定的换道动机逐渐减少，p=0.4与p=0.6的约束作用逐渐宽松，使大部分具有换道动机的换道行为得以实现，车速反而增大，并逐渐与其他速度曲线重合.

(4)外部因子p=0.8时表示约束宽松，对各种V/C值情况下的换道最终决策约束较小，对进入同步流以后的车速几乎不产生波动影响.

5 结 论

本文在分析影响驾驶员换道决策内外因子的基础上，提出了以内部因子为决策变量，外部因子为约束条件的机动车多车道换道模型，并将其引入一维改进舒适驾驶元胞自动机模型形成基于换道决策机理的多车道元胞自动机模型.对模型在不同内外部因子条件下的运行分析，发现系统中车辆平均换道次数由内外因子共同决定：不同饱和度条件下的车辆换道驾驶行为通过影响车辆加减速、匀速、怠速等运行工况从而影响车流平均速度，饱和度较小(V/C＜0.2～0.3)时，提高外部因子约束值可以提高平均车速；而饱和度较大(0.4＜V/C≤0.6)时适当宽松的外部因子约束有利于部分提高平均车速；饱和度很大(0.6＜V/C)时，外部因子会逐渐失去约束作用.运行结果表明，本文提出的多车道换道模型虽然考虑的内部因子较为简单，对外部因子进行了定性处理，但模型描述决策机理清晰，模型结构完整，具有较好扩展性；为建立通用、统一的多车道换道模型做了有益探索.

[1]RICKERT M,NAGEL K,SCHRECKENBERG M,et al.Two lane traffic simulations using cellular automata[J].Physica A Statistical Mechanics& Its Application,1996,231(4)：534-550.

[2]吴大艳,谭惠丽,等.三车道元胞自动机交通流模型研究[J].系统工程学报,2005,20(4)：393-397.[WU D Y,TAN H L,et al.Study on a three-lane cellular automata traffic flow model[J].Journal of Systems Engineering,2005,20(4)：393-397.]

[3]李娟,曲大义,刘聪,等.基于元胞自动机的车辆换道行为研究[J].公路交通科技,2016,33(11)：140-145.[LI J,QU D Y,LIU C,et al.Study on vehicle lanechangingbehaviorbased on cellularautomaton[J].Journal of Highway and Transportation Research and Development,2016,33(11)：140-145.]

[4]刘有军,曹珊.基于元胞自动机的强制换道模型研究[J].交通信息与安全,2009,3(27)：78-80.[LIU Y J,CAO S.Compulsory lane-changing traffic model based on cellular automaton[J]. Journal of Transport Information and Safety,2009,3(27)：78-80.]

[5]赵韩涛,毛宏燕.有应急车辆影响的多车道交通流元胞自动机模型[J].物理学报,2013,62(6)：53-60.[ZHAO H T,MAO H Y.Cellular automaton simulation of multi-lane traffic flow including emergency vehicle[J].Acta Phys.Sin,2013,62(6)：53-60.]

[6]张柠溪,祝会兵,林亨,等.考虑动态车间距的一维元胞自动机交通流模型[J].物理学报,2015,64(2)：299-305.[ZHANG N X,ZHU H B,LIN H,et al.Onedimensional cellular automaton model of traffic flow considering dynamic headway[J].Acta Phys.Sin,2015,64(2)：299-305.]

[7]JIANG R,WU Q S.Cellular automata models for synchronized traffic flow[J].JournalofPhysicsA General Physics,2003,36(2)：381-390.