考虑多前车反馈的智能网联车辆跟驰模型

秦严严，王 昊，冉 斌

(1.东南大学a.城市智能交通江苏省重点实验室，b.现代城市交通技术江苏高校协同创新中心，c.交通学院，南京210096；2.美国威斯康星大学麦迪逊分校土木与环境工程系，麦迪逊53706，美国)

0 引言

智能网联车辆(Connected and Autonomous Vehicle,CAV)基于车车通信技术，实时获取前车行驶状态，优化加速度输出，可从车辆微观层面改善交通流运营质量[1].CAV跟驰模型的研究可为未来大规模实地测试的实施提供模型参考，已成为交通流及智能交通领域的研究热点[2].

跟驰模型已发展60年，其中Newell模型[3]、优化速度模型(Optimal Velocity Model,OVM)[4]、广义力模型(Generalized Force Model,GFM)[5]、全速度差模型(Full Velocity Difference Model,FVD)[6]体现了速度优化的控制思想，逐渐被用于CAV跟驰模型的建模研究.已有研究成果较多地集中在FVD模型基础之上，考虑多前车间距变化项、速度差项、加速度项等不同条件建立了CAV跟驰模型[7-11].

Ioannou等[12]于1994年开展了电子节气门角度控制系统与车辆加速度输出之间的建模研究，建立的电子节气门角度与车辆加速度输出模型得到了较好应用[13].国内也有不少关于电子节气门控制的研究成果[14-15]，但是较多的还是关注控制系统的设计方面，缺乏与纵向跟驰模型之间的关联性研究.电子节气门角度作为未来CAV智能控制系统的核心变量，其与车辆运行的速度及加速度密切相关，因此，电子节气门角度的反馈能够起到实时感知前车运行状态的作用，进而提高后车的微观跟驰特性.然而，目前国内外基于电子节气门角度控制建立CAV跟驰模型的研究较少，文献[16]考虑最紧邻车辆电子节气门角度信息，尝试在FVD基础之上提出CAV跟驰模型，在一定程度上提高了常规车辆交通流稳定性.但是该模型没有考虑多前车电子节气门角度控制的影响，不能充分体现CAV具有的车联网特性.鉴于此，本文考虑多前车电子节气门控制，提出更加一般性的CAV跟驰模型，通过模型稳定性理论解析及数值仿真实验，分析所提模型对交通流稳定性与交通安全的影响作用.

1 跟驰模型

早在1961年，Newell[3]基于优化速度的思想提出了速度控制方程的跟驰模型，模型公式为

式中：V(⋅)为速度关于车头间距的优化速度函数；τ为反应延时；vn(t+τ)为第n辆车在t+τ时刻的速度；xn-1(t)、xn(t)分别为第n-1辆车、第n辆车在t时刻的位移.

1995年，Bando等[4]进一步提出了OVM模型，该模型为加速度控制公式，即

式中：α为敏感系数，本质上，1 α可视为OVM模型隐含的反应延时；vn(t)为第n辆车在第t时刻的速度.

鉴于OVM具有较大加速度等缺陷，Helbing等[5]于1998年提出GFM模型.姜锐等[6]考虑全速度差项，在GFM基础之上于2001年提出FVD模型，模型公式为

式中：λ为速度差系数；vn-1(t)为第n-1辆车在第t时刻的速度.

Li等[16]于2016年以FVD模型为基础，基于电子节气门角度控制，提出了针对CAV车辆的跟驰模型，记为T-FVD(Throttle-based FVD).模型公式为

式中：κ为电子节气门角度控制系数；θn-1(t)、θn(t)分别为第n-1辆车、第n辆车t时刻的电子节气门角度.

依据文献[12-13]，电子节气门角度与车辆速度、加速度可建立数学模型为

式中：b与c均为大于零的系数；ve为当前平衡态速度；θe为当前平衡态速度ve对应的电子节气门角度.

T-FVD模型由于考虑了前车与后车电子节气门角度差项，能够有效提升CAV交通流稳定性.基于车车通信技术，CAV车辆可实时获取车队前方多辆车行驶状态，进而更好地优化自身加速度输出.而T-FVD模型仅考虑了紧跟前车电子节气门角度信息，并未考虑多前车电子节气门角度控制的影响，未能充分体现CAV车辆在车联网环境下的车间通信特性.鉴于此，在T-FVD模型基础上，提出考虑多前车电子节气门控制的CAV跟驰模型，模型公式为

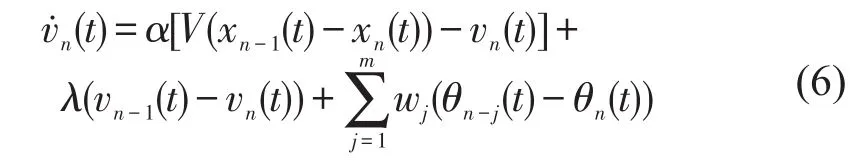
式中：m为前m辆车，且满足m＜n；wj为前j辆车电子节气门角度差项的权重系数，且满足0≤wj≤1.

可以看出，当m=1时，本文模型可退化为T-FVD模型；当m=0时，即不考虑前车电子节气门角度信息，本文模型退化为常规车FVD模型.并且，优化速度函数V可以选取不同的函数形式及参数.

2 模型稳定性解析

应用稳定性分析方法对所提CAV跟驰模型进行稳定性分析，为避免混淆，本文模型及推导过程中，用n-1表示车辆n的前车.初始状态下的车流处于平衡态，则CAV车辆位置坐标解为[17]

式中：se为平衡态车头间距；为第n辆车在t时刻平衡态位置；N为交通流中车辆总量.

在CAV车流平衡态添加扰动项rn(t)，即

式中：xn(t)为扰动影响下车辆的实际位移.

对式(8)求关于时间t的导数，可得

依据式(8)可得

式中：sn(t)表示车头间距，sn(t)=xn-1(t)-xn(t).

针对V[xn-1(t)-xn(t)]-vn(t)，应用一阶泰勒公式进行线性化展开，并将式(9)与式(10)带入，可得

针对vn-1(t)-vn(t)，依据式(9)可得

对扰动项求二阶导数可得，将其与式(11)、式(12)带入本文CAV跟驰模型式(6)中，得到

综上所述，2型糖尿病合并急性脑梗患者在饮食护理中使用饮食指导卡的效果显著，既可明显提高血糖控制情况和相关知识掌握度，又可改善患者生活质量和血脂情况，值得临床推广借鉴。

针对前m辆车电子节气门角度控制项，依据电子节气门角度控制式(5)，可得

依据式(14)，可得到

将式(15)带入式(13)，得到关于扰动项rn(t)的微分方程为

将扰动rn(t)写成傅里叶级数形式：rn(t)=Aexp(ikn+zt)，并带入式(16)展开，可化简得到

基于长波展开的假设，将z按照z=z1(ik)+z2(ik)2+…展开，并带入式(17)，求得(ik)平方项系数z2为

根据长波理论，若z2＞0，则CAV跟驰模型稳定.令z2＞0，可进一步化简得到CAV跟驰模型稳定应满足式(19).

由式(19)可知，当m=1时，可得到文献[16]中TFVD模型稳定性条件为

当m=0时，即不考虑前车电子节气门角度信息，本文CAV模型退化为FVD模型，相应的稳定性条件退化为FVD模型稳定性条件，即

因此，T-FVD模型相比于FVD模型，在区域内，CAV车辆可提升常规车辆交通流稳定性.本文所提CAV模型相比于T-FVD模型，可在区域内，进一步稳定CAV车辆交通流.并且，由式(19)可以看出，多前车数量m越大、权重系数wj越大，本文CAV模型稳定域越大；在相同取值条件下，j值越大，对应的权重系数wj对CAV模型稳定性的影响越大.稳定性的推导结果进一步证实了T-FVD模型为本文CAV模型的一个特例.

3 数值仿真实验

以交通安全冲突指标为依据，基于数值仿真实验，分析不同CAV车辆比例对交通安全的影响.其中，选取文献[18]中FVD模型的优化速度函数及参数标定结果，作为常规车辆跟驰模型，并选取m=3，得到具有3辆前车电子节气门控制的CAV车辆跟驰模型，进行数值仿真实验.

3.1 跟驰模型优化速度函数

Kesting等[18]应用城市交叉口环境中车辆轨迹数据对FVD模型进行了标定，采用FVD模型优化速度函数为

式中：v0为自由流速度；参数l和β确定优化函数V的曲线形状.

FVD模型标定结果为如表1所示，文献[18]验证了该标定结果可较好地反应常规车辆在城市交叉口环境中的驾驶跟驰特性.

表1 FVD模型参数取值Table 1 Parameter values of FVD model

对于CAV车辆而言，以m=3为例，得到3辆前导车电子节气门控制的CAV车辆跟驰模型.式(5)中系数b和c取值[16]为：b=0.8，c=0.27.依据文献[17]中对前车信息系数取值的研究结果，本文取值为：w1=0.1，w2=0.05，w3=0.03.

在上述模型参数具体取值情况下，依据模型稳定性判别式(19)可求得本文选取的常规车模型，以及3辆前导CAV模型各自稳定与否的平衡态速度范围.方便起见，将式(19)改写为

式中：f记为模型稳定性条件，当f＞0时，稳定；反之，则不稳定.将模型参数带入，可计算得到常规车与3辆前导CAV车辆稳定的速度范围，如图1所示.

图1 跟驰模型稳定性Fig.1 Stability of car-following models

由图1可知，在自由流速度范围以内(0～18.1 m/s)，常规车仅在0～1.6 m/s及16.3～18.1 m/s较小速度范围内稳定，在1.6～16.3 m/s较大速度范围内均不稳定；而3辆前导CAV车辆在5.5～12.3 m/s的速度范围内不稳定，在其他速度范围内稳定.

3.2 安全评价指标

选取文献[19]中基于TTC(Time-to-collision)得到的TET(Time Exposed Time-to-collision)和TIT(Time Integrated Time-to-collision)作为仿真实验中的安全评价指标.TET和TIT指标是目前交通流车辆尾部碰撞安全风险的主流评价指标，计算公式为[20]

式中：L为车长，取为5 m；τsc为仿真步长，本文取0.1 s；TTC*为TTC指标阈值，一般取为1～3 s.

TET和TIT指标值越小，表明安全性越高，可以看出，TET指标侧重于描述存在冲突风险的次数，而TIT指标侧重于描述冲突风险的严重程度.

3.3 仿真结果

如前所述，常规车FVD模型参数取值选取了基于城市交叉口环境的车辆轨迹数据标定结果[18]，而交叉口红灯启停、绿灯启亮的过程中存在较多的车辆尾部碰撞安全风险隐患[21].因此，参照文献[21]进行安全性仿真实验设计：在单车道开放性边界条件下，距道路起点225 m处设有信号灯，信号灯上游20 m为停车线.在初始状态，车队共有20辆车，车队初始速度为12.87 m/s，信号灯绿灯亮，尔后变为红灯，红灯时间为60 s，然后再恢复为绿灯，红灯可模拟成停车线上静止的车辆，详细实验设计可参见文献[21].仿真实验中统计在上述红灯启停、绿灯启亮的过程中车辆尾部碰撞安全风险指标TET和TIT，且在统计TET和TIT指标时，针对阈值TTC*取值 1.0 s、1.5 s、2.0 s、2.5 s、3.0 s做参数敏感性分析.同时考虑仿真中的随机性，对每次仿真均独立重复3次，并取均值作为仿真结果.

仿真实验结果如表2和表3所示，表2为不同CAV比例下TET指标情况，表3为TIT指标情况.表2和表3中数据的含义是，以CAV比例为0时的安全风险指标TET和TIT为基准，其他不同CAV比例时，安全风险隐患降低的百分比.由表2和表3可以看出，CAV车辆比例的增加，可逐渐减低车辆尾部碰撞安全风险隐患.当CAV车辆比例达到100%时，尾部碰撞安全隐患可降低99%，不可否认的是，TET和TIT作为安全性影响分析的仿真模拟化替代手段，具有一定的局限性，其仿真结果可看出定性化的影响趋势，对于安全性风险的量化评价，还需依赖未来大规模CAV真车实验的实施.

表3 TIT指标下的安全影响Table 3 Safety impacts underTITindicator

4 结论

(1)本文提出了考虑多前车电子节气门角度控制的CAV跟驰模型，模型结构具备一般性，使得已有CAV车辆T-FVD模型及常规车辆FVD模型均是本文所提模型的特例，且本文所提模型具有更优的稳定域.

(2)模型稳定性理论解析表明，考虑的前车数量越多、电子节气门角度控制权重系数越大，所提模型稳定性越好.前车位置越远，其电子节气门角度控制权重系数在相同取值条件下，对所提模型稳定性的影响越大.

(3)数值仿真实验表明，在CAV市场率逐步普及阶段，所提CAV模型可逐渐降低混合交通流中车辆尾部碰撞安全风险隐患，可为未来大规模真车实验的实施提供模型参考.

(4)多前车行车状态数据的传递，以一定概率的传递失效情况值得考虑，该情况下的CAV跟驰建模工作将是下一步的研究.

[1]秦严严,王昊,王炜,等.自适应巡航控制车辆跟驰模型综述[J].交通运输工程学报,2017,17(3)：121-130.[QIN Y Y,WANG H,WANG W,et al.Review of carfollowing models of adaptive cruise control[J].Journal of Traffic and Transportation Engineering,2017,17(3)：121-130.]

[2]秦严严,王昊,王炜,等.混有CACC车辆和ACC车辆的异质交通流基本图模型[J].中国公路学报,2017,30(10)：127—136.[QIN Y Y,WANG H,WANG W,et al.Fundamental diagram model of heterogeneous traffic flow mixed with cooperative adaptive cruise control vehicles and adaptive cruise control vehicles[J].China Journal of Highway and Transport,2017,30(10)：127—136.]

[3]NEWELL G F.Nonlinear effects in the dynamics of car following[J].Operations Research,1961,9(2)：209-229.

[4]BANDOM,HASEBEK,NAKAYAMAA,etal.Dynamical model of traffic congestion and numerical simulation[J].Physical Review E,1995,51(2)：1035-1042.

[5]HELBING D,TILCH B.Generalized force model of traffic dynamics[J].Physical Review E,1998,58(1)：133-138.

[6]JIANG R,WU Q,ZHU Z.Full velocity difference model for a car-following theory[J].Physical Review E,2001,64(1)：017101.

[7]TANG T Q,ZHANG J,CHEN L,et al.Analysis of vehicle's safety envelope under car-following model[J].Physica A：Statistical Mechanics and its Applications,2017(474)：127-133.

[8]YU S,SHI Z.The effects of vehicular gap changes with memory on traffic flow in cooperative adaptive cruise control strategy[J].Physica A：Statistical Mechanics and its Applications,2015(428)：206-223.

[9]唐毅.基于前后多车信息的跟驰模型及其车流平稳性控制研究[D].重庆：重庆大学,2014.[TANG Y.Study on the car following model and its smoothness control based on the information of preceding and following vehicles[D].Chongqing：Chongqing University,2014.]

[10]YU G,WANG P,WU X,et al.Linear and nonlinear stability analysis of a car-following model considering velocity difference of two adjacent lanes[J].Nonlinear Dynamics,2016,84(1)：387-397.

[11]李修云,周桐,杨智勇.基于最紧邻前车加速度信息的跟驰模型[J].重庆大学学报(自然科学版),2015,38(6)：153-158.[LI X Y,ZHOU T,YANG Z Y.Carfollowing model based on the information of the nearestneighbor leading car's acceleration[J].Journalof Chongqing University,2015,38(6)：153-158.]

[12]IOANNOU P,XU Z.Throttle and brake control systems for automatic vehicle following[J].Journal of Intelligent Transportation Systems,1994,1(4)：345-377.

[13]LI K,IOANNOU P.Modeling of traffic flow of automated vehicles[J]. IEEE Transactions on Intelligent Transportation Systems,2004,5(2)：99-113.

[14]王耀南,申永鹏,孟步敏,等.车用汽油发动机电子控制系统研究现状与展望[J].控制理论与应用,2015,32(4)：432-447.[WANG Y N,SHEN Y P,MENG B M,et al.Electronic control system for gasoline automotive engine：state of the art and perspective[J].Control Theory&Applications,2015,32(4)：432-447.]

[15]郑太雄,杨斌,李永福,等.车联网环境下电子节气门全局快速滑模控制[J].仪器仪表学报,2014,35(10)：2356-2364.[ZHENG T X,YANG B,LI Y F,et al.Global fast sliding mode controller for electronic throttle vale under the environment of IoV[J].Chinese Journal of Scientific Instrument,2014,35(10)：2356-2364.]

[16]LI Y,ZHANG L,PEETA S,et al.A car-following model considering the effect of electronic throttle opening angle under connected environment[J]. Nonlinear Dynamics,2016,85(4)：2115-2125.

[17]LI Z,LI W,XU S,et al.Stability analysis of an extended intelligent driver model and its simulations under open boundary condition[J].Physica A：Statistical Mechanics and its Applications,2015(419)：526-536.

[18]KESTING A,TREIBER M.Calibrating car-following models by using trajectory data：Methodological study[J].Transportation Research Record：Journal of the Transportation Research Board,2008(2088)：148-156.

[19]MINDERHOUD M M,BOVY P H L.Extended time-to-collision measures for road traffic safety assessment[J].Accident Analysis&Prevention,2001,33(1)：89-97.

[20]秦严严.自适应巡航控制系统对交通安全的影响研究[J].徐州工程学院学报(自然科学版),2017,32(4)：46-49.[QIN Y Y.Study on impacts of adaptive cruise control system on traffic safety[J].Journal of Xuzhou Institute ofTechnology (NaturalSciences Edition),2017,32(4)：46-49.]

[21]YU S,SHI Z.An improved car-following model considering relative velocity fluctuation[J].Communications in Nonlinear Science and Numerical Simulation,2016(36)：319-326.