高斯支持向量机在家具板材分类识别中的应用

何金彬，傅惠南，黄辰阳，潘奕创

（广东工业大学 机电工程学院，广州 510006）

随着我国工业自动化水平的不断提高，越来越多的生产线引入自动识别系统，家具板材的加工产线就是其中之一。不同类别的家具板材有着不同的图像纹理信息。纹理识别算法的研究也多种多样，如：文献[1]的基于灰度共生矩的纹理识别分类方法，通过提取图片纹理的灰度共生矩作为竞争神经网络的输入参数进行训练，最后输出分类结果；文献[2]提出二维离散小波变换和支持向量机相结合的方法，利用图像生成的小波以及局部能量作为表征图像的纹理特征；文献[3]的监督式多尺度的贝叶斯分类法，采用双树复小波变换获得的多尺度副值表征图像的纹理特征；文献[4]针对新的纹理分类智能系统，提出采用遗传算法、离散小波变换和神经网络相结合的方法；文献[5]的基于改进高斯马尔可夫随机场的纹理特征方法，对高维空间分辨率的图像进行分类。

这些方法对单色图像的纹理特征都有较好的识别效果，但对家具板材的分类仍存在问题：①纹理相同，颜色不同的板材会误归为一类；②纹理和颜色都一样的同种板材因图案差异而误分为两类或多类。对此，收集彩色图片，将图片从RGB颜色空间转换到 HSV（hue，saturation，value）颜色空间后提取纹理特征参数，利用高斯混合模型的概率统计能力及支持向量机的分类判决能力进行识别。

1 家具板材分类原理

家具板材根据颜色、纹理、图案不同进行分类，其中纹理信息是主要决定因素。针对同纹理不同颜色误分为一种类别的情况，将彩色图片从RGB（red，green，blue）颜色空间转换到 HSV 颜色空间后提取板材纹理特征参数进行分类识别。对同颜色同纹理，图案有差异但为同类板材的情况，文中运用一种基于集成高斯支持向量机的方法进行分类识别。

假设 X=｛x1，x2，…，xn｝为表征图像特征的参数集，将其输入到高斯混合模型中，得到输出参数集X′=｛x1′，x2′，…，xn′｝，将参数集进行适当变换后输入支持向量机模型，得到目标变量

Y=f（x1′，x2′，…，xn′）

式中：n为板材特征属性的个数；Y为家具板材的类型集合。可以得到X→Y的映射关系。该映射过程就是整个分类方法的建模过程，即高斯支持向量机模型。该方法分类原理如图1所示。

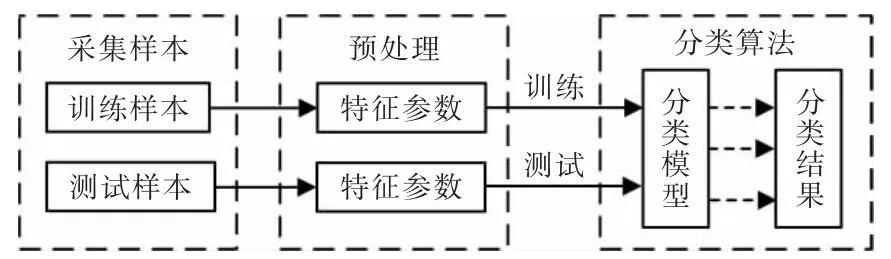
图1 高斯支持向量机算法分类原理Fig.1 Gauss support vector machine algorithm classification principle

2 高斯支持向量机的算法原理

2.1 高斯模型

由概率统计理论及文献[6]可知，有限个高斯函数的线性组合可以逼近任意的概率密度函数。同理有限个高斯函数也可以对家具板材的纹理特征进行比较精确的描述。假设M阶高斯模型的概率密度函数为

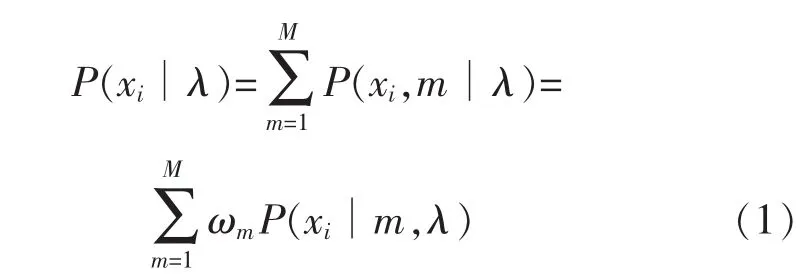
M阶高斯混合模型的概率分布密度函数为

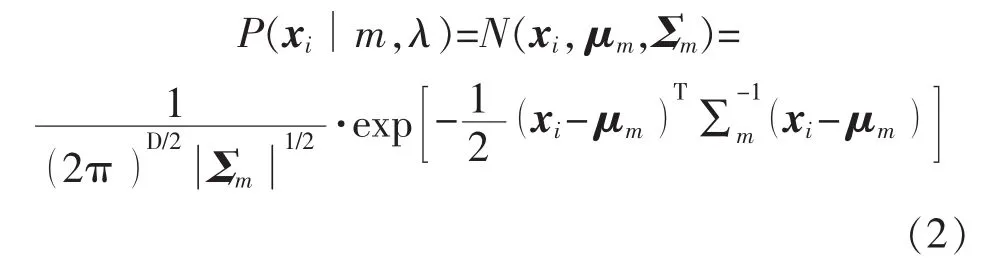
式中：λ为高斯模型的参数集；m为隐状态号，即高斯分量序号，M阶高斯就有M个隐状态；xi为D维的图像特征矢量；ωm为m个分量的混合权值，其值对应为隐状态m的先验概率；μm为均值矢量；Σm为协方差矩阵；D为特征矢量的维数。

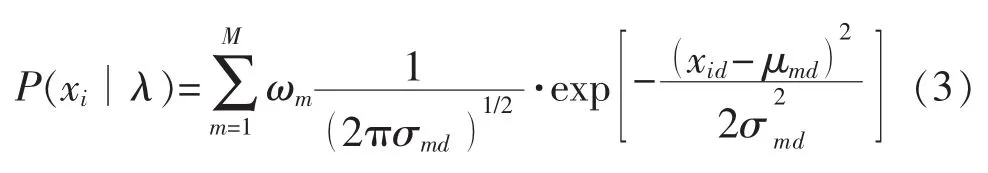
式中：xid， μmd分别为矢量 xi和 μm的第 d 个分量；M为模型的混合度。

由于高斯混合模型输出的是一个M阶D维的特征参数矩阵，而支持向量机的输入参数只能是固定维数的特征向量[7]，故文中提出一维输出高斯混合模型的方法。

D个样本观察数据在由M个单高斯模型组成的混合高斯模型处理后，输出M阶D维的概率矩阵XDM。 对 XDM进行 PCA[8]主成分分析得到 XD′M′，再将进行变换，将第2行数据排在第1行之后，第3行数据排在第2行之后，以此类推直至所有行数据重新排列完整，得到新数据：

X1（dm）′=（x11，…，x1m，x21，…，x2m，…xd1，…，xdm）

其推导过程如下：

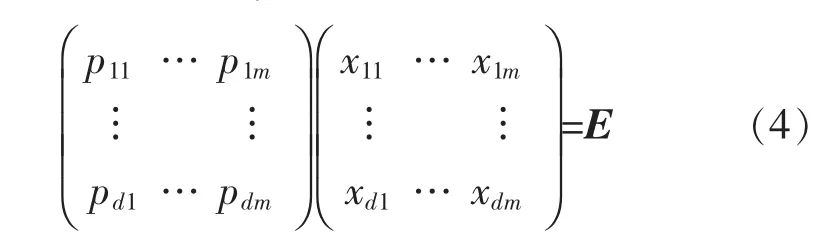
其中

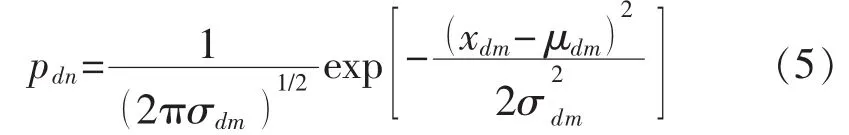
由EM算法得到高斯混合模型概率输出矩阵为

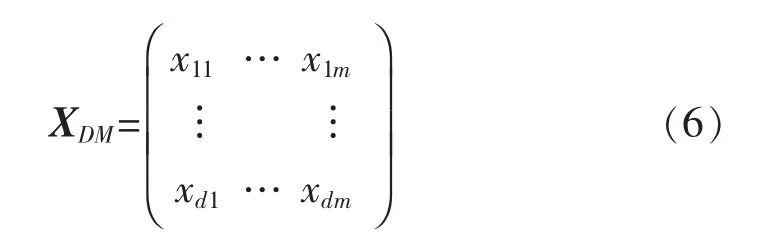
将进行变换后

X1（dm）′＝（x11，…，x1m，x21，…，x2m，…xd1，…，xdm）将高斯混合模型的输出参数X1（dm）′作为支持向量机的输入训练集进行分类识别。

2.2 支持向量机模型

支持向量机SVM（support vector machine）是在统计学的VC（Vapnik-Chervonenkis）维理论和结构风险最小化的基础上，对训练样本求取最优分类平面而提出的[9]。对于线性可分的二分类问题，能找到一个使得两类样本点以最大分类间隙分开的平面，称为最优分类平面。假设，有两类待分类的样本数据｛xi，yi｝，i=1，2，…，n，xi∈Rd，yi∈｛-1，+1｝。 若存在一个超平面H：ωx+b=0，可将两类数据以最大分类间隔分类，即满足方程：

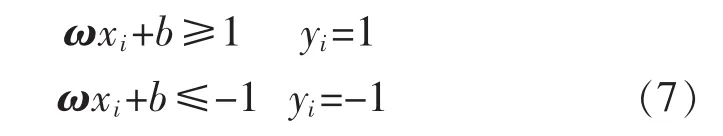
式中：ω为权重向量；b为最优分类超平面的偏移量。

在实际应用中，并非所有数据样本都线性可分。对于线性不可分的情况，通过引入核函数可将样本数据从低维空间映射到高维空间，从而使数据线性可分。设核函数

K（xi，yi）＝φ（xi）φ（yi）

则可得最优分类超平面方程为

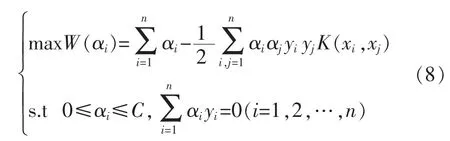
式中：C为惩罚参数[9]，其大小由用根据实际经验设定。方程组（8）的解可由拉格朗勒乘数法求得

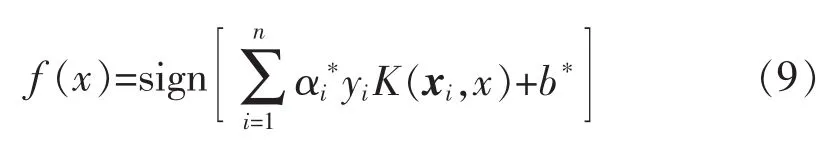
式中：xi为支持向量；为支持向量对应的拉格朗勒乘子；b*为常数[10]。

2.3 纠错码支持向量机

支持向量机是为解决二分类问题而提出的。文中采用二进制纠错码，将多类分类问题转化为多个二分类问题[11]。对于k类分类问题，对每个类别进行一个长度为L的二进制编码，能形成一个K行L列的码本。对于其中第i列，将该位中编码为“1”的所有类别归为一类，其他编码为“0”的类别作为另一类，因此每个编码对应一个两类分类问题，这样k类分类问题就转化为了L个两类分类问题。

对于一个新样本分类时，L个支持向量机分类器的分类结果（1或0）构成一个码字s，再计算码本内K个编码与s的汉明距离，距离最小者所所属的类别就是该测试样本所代表的类别。

3 试验结果和分析

3.1 样本采集

为了验证文中所述方法的有效性，在MatLab仿真软件中对纹理分类效果进行评估。采集30种不同板材的纹理特征彩色图片共1500张，每类各50张，每张图片大小为640×480。为了进一步增加样本图片的数量，将每张图片分割为320×240大小的子图片4张。最终得到30种不同纹理特征的彩色图片，每种200张，共6000张图片。

对每张大小为320×240的彩色子图片进行颜色空间转换，得到HSV彩色纹理图片。

3.2 特征参数集的选择

选择合适的特征参数，不仅能表征图像的纹理信息，还能更好地区分不同的纹理类别。在此选取彩色图像HSV颜色空间的如下信息作为特征参数：灰度共生矩、角二阶矩、熵、相关性、对比度、能量、惯性矩、3×3窗口大小的灰度均值和标准偏差[12]。

文献[13]指出，彩色RGB颜色空间的3个单色分量之间有较高的相关性，直接利用RGB分量难以得出理想效果。鉴于此，文中把彩色RGB与HSV颜色空间的样本分类识别率进行比较。将RGB彩图的R通道图像的特征参数集记为Fr；G通道图像的特征参数集记为Fg；B通道图像的特征参数集记为Fb。

为进一步说明不同特征参数对纹理分类效果的影响，提取了R通道图像的灰度共生矩、角二阶矩、熵，G通道图像的相关性、对比度、能量，B通道图像的惯性矩、灰度均值、标准偏差，作为混合特征参数集，记为Fs。再选择HSV颜色空间的特征参数集，记为 Fh。

分别提取出 Fr，Fg，Fb，Fs，Fh的特征参数集作为高斯混合模型的输入参数集。经过高斯混合模型处理后，输出的特征向量分别为

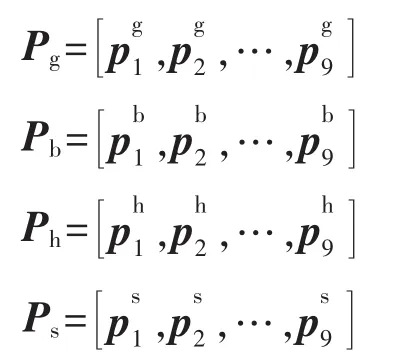
将得到的高斯混合模型输出概率参数集，作为支持向量机的输入参数集，进行分类。

3.3 不同参数选择的影响

3.3.1 核函数的选择

为验证不同核函数对纹理分类的影响，选择Fr作为特征参数集。在其他试验条件相同的情况下，分别选择高斯核函数、多项式核函数、Sigmoid核函数作为支持向量机的核函数，在不同的分类类别下观察识别率的变化。不同核函数分类效果情况见表1。

表1 3种核函数的识别率对比Tab.1 Comparison of recognition rate between three kernel functions

分析表1数据可知，选用高斯核函数的效果，比多项式核函数、Sigmoid核函数的总体效果更好。

3.3.2 γ和L的选择

考虑高斯核函数参数γ和扩展多分类中的编码长度L对纹理识别率的影响。分别令γ=0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0， 对试验数据进行测试。其试验统计数据见表2。

分析表2数据可知，当分类类别K=25，编码长度L=51，γ=0.9或1.0时纹理分类识别率较好。3.3.3 纹理特征参数的选择

为了验证纹理特征参数的选择对纹理识别率的影响。试验选用高斯核函数、L=51，K=25，惩罚参数C=1000， 在不同的γ值下， 分别选用Fr，Fg，Fb，Fh，Fs的特征参数集作为高斯支持向量机的输入参数集，其纹理识别率的对比效果如图2所示。

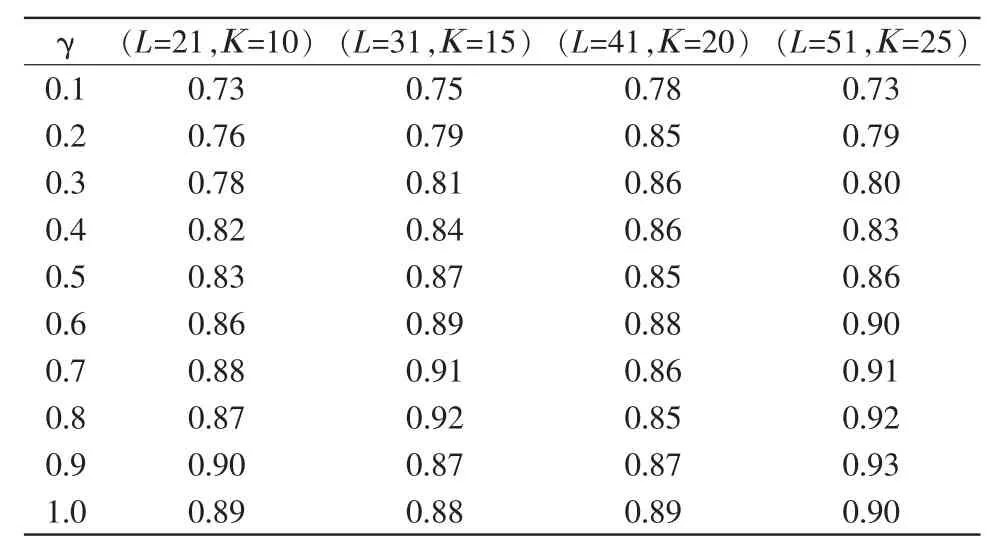
表2 不同L和γ的识别率对比Tab.2 Comparison of recognition rate of different L and γ

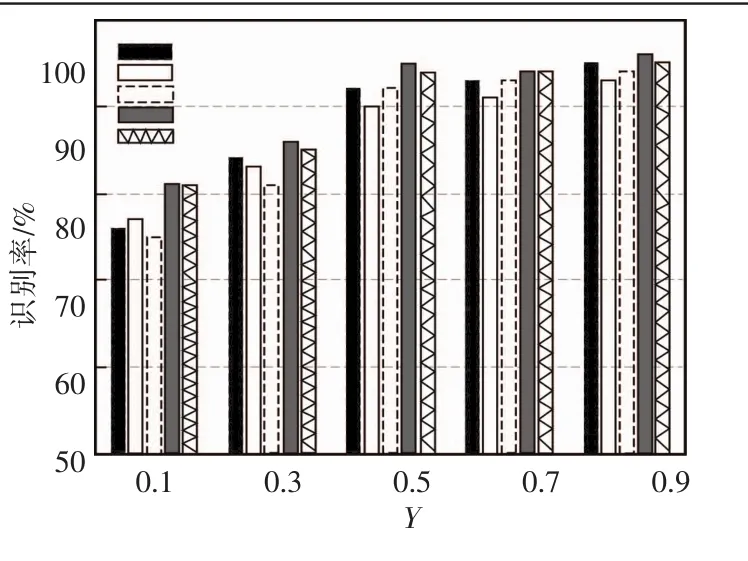
图2 不同特征集的GMM-SVM识别效果Fig.2 GMM-SVM recognition effect of different feature sets

由图可见，当混合特征参数集Fs为图像的纹理特征时，其识别率是最高的。表明在家具板材的分类识别中，彩色HSV颜色空间的特征集能更好地表征图像纹理特性。

3.4 纹理特征分析

针对同纹理不同颜色误归为一类的情况（如图3所示），将RGB彩图转换到HSV颜色空间下进行处理。

图3 同纹理不同颜色的不同板材Fig.3 Different plates with different colors in same texture

针对同种板材因图案差异误分为两类或者多类的情况 （如图4所示），将纹理图像做傅里叶变换，再进行滤波。 图 4（a），4（b）两图的纹理差异在于图案，只需抑制图4（a）中的文字图案信息特征即可。图4（c）是图4（a）的傅里叶变换频谱图，用理想滤波器对图4（c）进行低通滤波，得到图 4（d），再对其进行傅里叶反变换。最后，将滤波处理后的图像输入到高斯支持向量机模型中，进行分类识别。

图4 有图案差异的同种板材及其傅里叶变换图谱Fig.4 Same sheet with different patterns and its Fourier transform atlas

3.5 不同分类算法的识别率对比

为了验证方法的有效性，选择Fs作为表征图像的特征参数集，分别用高斯混合模型算法、支持向量机分类器、高斯支持向量机算法、贝叶斯分类算法和人工神经网络算法进行试验。将板材样本的训练比例分别设为10%，20%，30%，观察其识别率（如图5所示）的变化。

图5 不同方法识别效果的对比Fig.5 Comparison of different methods to identify the effect

由图5可见，高斯支持向量机的分类算法相比高斯模型算法、支持向量机分类器、贝叶斯分类算法有更高的识别率；高斯支持向量机和人工神经网络算法之多层感知器都有很高且相近的识别率。将板材样本的输入数量设为50～500，观察在不同的样本数量下高斯支持向量机算法和人工神经网络算法的运行时间，如图6所示。

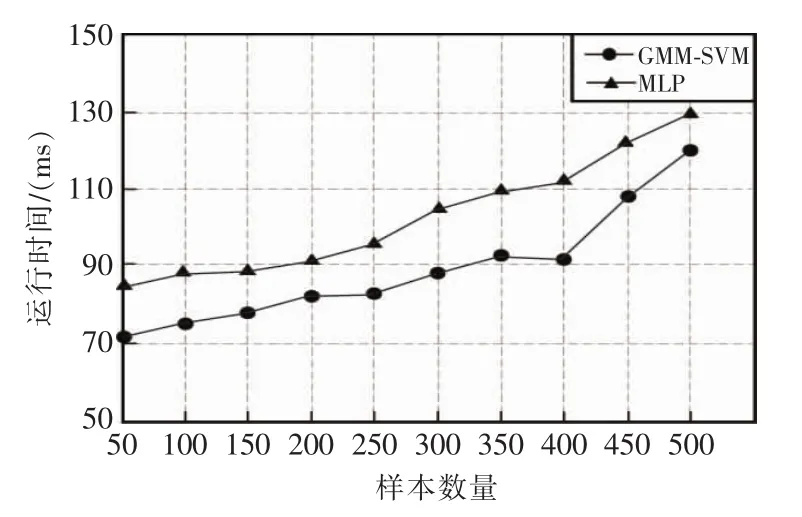
图6 GMM-SVM和MLP的效率对比Fig.6 Efficiency comparison of GMM-SVM and MLP

由图可见，高斯支持向量机GMM-SVM的运行时间在72～122 ms，人工神经网络之MLP的运行时间在87～129 ms。由此表明，在板材分类识别中，高斯支持向量机的方法具有更高效率。

4 结语

文中应用基于高斯混合模型和支持向量机结合的纹理识别方法，利用高斯混合模型统计出的特征概率矩阵作为支持向量机的输入特征向量，既利用了高斯混合模型良好的统计能力，又利用了支持向量机良好的判别能力。尤其在本例的板材分类中，针对同纹理不同颜色的样品有较好的识别率，也降低了同种样品误分类的概率。该方法比单一的高斯混合模型、支持向量机、贝叶斯的效果更好，具有较强的鲁棒性和较好的推广泛化能力。

[1] Bai X B，Wang K Q，Hui W．Research on the classification of wood texture based on Gray Level Co-occurrence Matrix[J]．Journal of Harbin Institute of Technology，2005，37（12）：1667-1670．

[2] Rajpoot K M，Rajpoot N M．Wavelets and support vector machines for texture classification[C]//International Multitopic Conference，2004，24（11）：328-333．

[3] Celik T，Tjahjadi T．Bayesian texture classification and retrieval based on multiscale feature vector[J]．Pattern Recognition Letters，2011，32（2）：159-167．

[4] Avci E，Sengur A，Hanbay D．An optimum feature extraction method for texture classification[J]．Expert Systems with Applications，2009，36（3）：6036-6043．

[5] Zhao Y，Zhao L，Li P，Huang B．Classification of high spatial resolution imagery using improved gaussian markov random-fieldbased texture Features[J]．IEEE Transactions on Geoscience and Remote Sensing，2007，45（5）：1458-1468．

[6] Ito K，Xiong K．Gaussian filters for nonlinear filtering problems[J]．Automatic Control IEEE Transactions on，2000，45（5）：910-927．

[7] 周兴恩．基于GMM和SVM的音频分类算法[D]．大连：大连理工大学，2008．

[8] 王松，夏绍玮．一种鲁棒主成分分析（PCA）算法[J]．系统工程理论与实践，1998，18（1）：9-13．

[9] Kim K I，Jung K，Park S H，et al．Support vector machines for texture classification[J]．IEEE Transactions on Pattern Analysis＆ Machine Intelligence，2002，24（11）：1542-1550．

[10] 杨云，卢美静．基于集成支持向量机的葡萄酒品质分类方法[J]．计算机工程与设计，2017，38（9）：2541-2545．

[11] Kindermann J，Leopold E，Paass G．Multi-class classification with error correcting codes[EB/OL]．http：//www．researchgate．net．

[12] 冯建辉，杨玉静．基于灰度共生矩阵提取纹理特征图像的研究[J]．北京测绘，2007，21（3）：19-22．

[13] 肖淑苹，杨建雄，陈一栋．基于小波概率神经网络的彩色纹理识别[J]．微电子学与计算机，2010，27（6）：28-31． ■