大型客机增升装置噪声机理与噪声控制综述
2018-06-29李伟鹏
李伟鹏
(上海交通大学 航空航天学院, 上海 200240)
0 引 言
气动噪声问题是大型客机研制过程中的关键问题之一,直接关系到大型客机的适航、环保性(声污染)和安全性(声疲劳)。2006年国际民航组织(ICAO)施行了严格的第4阶段噪声控制标准(如图1所示),即比第三阶段噪声控制标准再降低10 dB[1],使得大型客机适航取证更加严峻。同时,安静舒适的机舱环境可提高大型客机的市场竞争力,低噪声标准也可降低声疲劳导致的安全不确定性。增升装置噪声是机体噪声的主要噪声源,是大型客机总体噪声水平的重要组成部分。目前,大型客机大多采用前缘缝翼、后缘襟翼增升构型,在满足起飞和降落阶段升阻比特性、抑制失速的同时,其产生的气动噪声增加了大型客机的总体噪声水平。而近年来大涵道比发动机设计,大幅降低了发动机的噪声水平,使得机体噪声(主要包括增升装置噪声和起落架噪声)成为大型客机在起飞和降落阶段的主要噪声源[2-4]。如图2所示,在大型客机降落阶段,机身噪声的有效感觉声压级(EPNL)要超过发动机噪声,起落架噪声是机身噪声中最为重要的声源,缝翼噪声和襟翼噪声占据了机身噪声的较大比重;无论是缩比模型实验[5-7],还是真实飞行测试[8],缝翼和襟翼噪声均被认为是大型客机起飞和降落过程中主要的噪声源。我国大型宽体客机仍处于攻坚阶段,增升装置噪声机理与降噪技术是工程中面临的关键问题之一[9-15]。揭示缝翼和襟翼噪声机理,实施低噪声设计和噪声控制,有助于掌握“静音飞机”的关键设计技术,有利于加快大型客机的适航取证,并降低声污染和声疲劳导致的不良后果。
增升装置噪声是一类多尺度、非定常、复杂的流动现象,包括层/湍流边界层分离、剪切层混合和剪切层与壁面干扰等典型的流体力学问题。气动噪声是随时空变化的弱小压力脉动,包括噪声产生、近场传播和远场辐射等特性,噪声的能量级别远小于流场内部的湍流脉动,且噪声的时间和空间尺度与模型特征尺度存在较大的差异,给气动噪声理论研究增加了难度。开展增升装置噪声机理和噪声控制的研究,可加深对流体力学多尺度、非定常问题的描述和理解,可进一步阐述涡流、雷诺应力及湍流脉动等参数与气动噪声的关联。
1 增升装置噪声机理研究现状分析
1.1 缝翼噪声机理
围绕缝翼噪声的研究,国外已经开展了30余年,并取得众多成果,综述性文章可参考文献[2,7-8]。缝翼的流动特征主要包括(参考图3):①缝翼前缘的流动分离;②剪切层的转捩及湍流不稳定性的非线性增长;③剪切层与缝翼壁面的撞击与干扰;④回流区的不稳定振荡;⑤缝翼尾缘的剪切层混合。根据噪声频谱特性,缝翼噪声可分为宽频噪声和啸音,如图4所示,其中宽频噪声的峰值分布于1≤St≤3之间(St=fCs/U∞,Cs为缝翼弦长,U∞为来流速度),而啸音包括低频啸音(1≤St≤3)和高频啸音(10≤St≤20)。
缝翼低频啸音的产生机理尚不清楚,主要观点包括:(1)根据几何相似原理,Kolb等[16]认为缝翼低频啸音的产生与开式空腔噪声相似,是一种涡声耦合反馈机制[17],即剪切层中大涡结构间歇性的撞击壁面而产生高强度噪声,噪声反向传播并激励缝翼前缘剪切层,诱导产生新的起始大涡结构。Jenkins等[18]利用PIV技术分析了缝翼剪切层中大涡结构的演化过程,指出大涡结构在近壁区的撞击与摆动是诱发缝翼低频噪声的主要原因。König等(2010)[19]开展了混合LES/CAA数值计算,通过互相关性分析指出缝翼缝道的压缩波在缝翼尾缘和主翼表面之间具有一种流动-噪声反馈机制。(2) Dobrzynski等[3]实验发现缝翼上表面的压力脉动与缝翼缝道的压力脉动的相关性系数高达0.7,指出低频啸音的产生源于缝道区的非定常流量振荡,即狭缝共振机制。(3) Imamura等[20-21]开展了混合RANS/LES计算,利用凹坑流线填充技术,缝翼低频啸音被完全消除,指出剪切层不稳定性是产生低频啸音的主要原因。Khorrami等[22]通过非定常RANS计算得出,剪切层中大涡结构的产生受制于Kelvin-Helmholtz不稳定性,认为缝翼低频噪声源于剪切层中的Kelvin-Helmholtz不稳定性。
缝翼高频啸音可能比其它噪声源具有更高的声压级强度(模型实验中),其产生机理亦存在学术争议。Storms等[23]在缩比模型实验中,观测到高频啸音随缝翼缝道尺寸减小而向低频段偏移,但不能被完全消除,直到缝道堵死,指出高频啸音与缝道区流动不稳定性具有直接联系。Khorrami等[24]开展了非定常RANS计算,发现缝翼尾缘卡门涡街频率与高频啸音频率一致,认为高频啸音的产生源于缝翼尾缘的涡脱落机制。Tam & Pastouchenko[25]指出涡脱落可产生高频啸音,但尾缘涡的形成受制于噪声反馈激励,并非单纯的剪切层不稳定性。Agarwal & Morris (2002)[26]提出一种类似口哨噪声机制来解释高频啸音的产生,当缝道流动的固有模态受到外界扰动的激励时,可产生高频啸音。Takeda等(2004)[27]利用URANS/FWH方法,分析了一种理想缝翼的噪声组成,指出高频啸音的产生需要流动与噪声之间的反馈作用。Makiya等[28]实验研究了低雷诺数条件下的缝翼噪声机理,认为缝翼高频啸音的产生是由于缝翼上表面边界层与噪声压力波之间存在闭环耦合振荡机制。
由上可知,缝翼噪声的产生机理存在多种解释,汇总如图5所示。低频啸音的产生机理有三种主流观点,即涡声耦合反馈机制、窄缝共振机制和剪切层固有不稳定性;高频啸音的产生存在着两种学术争议,即尾缘卡门涡脱落和流动-噪声干扰。在缝翼非定常流场中,边界层/剪切层不稳定性、涡结构的产生/脱落/混合机制、涡与壁面干扰是产生噪声的主要因素,可能是一种因素主导,也可能是多种因素共同作用。同时,缝翼非定常流场受到噪声的反馈激励,流场与声场之间存在较强的耦合作用。揭示缝翼噪声机理,关键是探究缝翼非定常流动与噪声之间的多尺度时空关联,识别噪声源,并确定噪声信号与噪声源之间的关系。
1.2 襟翼噪声机理
襟翼噪声主要包括两个组成部分,即襟翼横断面上的非定常流动和襟翼侧缘的涡脱落机制,如图6所示。在襟翼横断面上,流场特征与缝翼相似,但随着偏转角的增大,襟翼尾缘常发生流动分离,附带产生非定常湍流脉动和低频高强度噪声;在襟翼侧缘,气流上洗而形成大尺度的涡流结构,伴随着涡生成、涡混合、涡撞击壁面和涡脱落等复杂的流动现象,襟翼侧缘噪声被认为是襟翼噪声的主要因素。
早在1979年,Fink and Schlinker(1979)[29]通过实验表明襟翼侧缘是机身噪声的重要组成部分。McInemy等(1986)[30]证实了襟翼翼尖区域存在剧烈表面压力脉动,并指出压力脉动的形成与剪切层中相干结构具有直接的联系。Khorrami & Singe(1998)[31]利用不稳定性理论,分析指出侧缘剪切层不稳定波是噪声产生的主因。Radeztsky等(1998)[32]实验测量了不同偏转角下的流场,发现了在襟翼侧缘存在涡对结构(主涡与二次涡),并通过对涡核位置及涡强度的测量,发现在大偏转角条件下涡破碎机制可诱发噪声的产生。针对Radeztsky等(1998)的实验结果,Khorrami等(1999)[33]利用RANS计算证实了剪切层中涡对结构的存在,并分析了涡对结构的空间演化过程。Dong等(1999)[34]利用CFD/CAA混合方法,分析了剪切层不稳定波与襟翼上下壁面的干扰作用,指出了可能存在三种致声机理,即剪切层不稳定波与襟翼壁面的干扰、不稳定波间的相互作用和湍流脉动在侧缘尖角处的溃散。Brooks & Humphreys(2003)[35]通过实验发现前缘涡对结构在下游融合并向远离表面发展,指出襟翼侧缘噪声的产生主要依赖于剪切层内部固有的不稳定模态,且低频噪声源于非定常的涡脱落机制。Guo(2013)[36]建立了预测襟翼侧缘噪声理论模型,在模型中假设了流动分离和涡-壁面干扰两种噪声机理。
2 增升装置噪声控制研究现状
利用主/被动流动控制技术,众多学者开展了增升装置噪声控制研究,综述文章可参考[37-40]。本文对近年来的缝/襟翼降噪方法进行了汇总,详见表1和表2,典型缝/襟翼降噪方法如图7和图8所示。

表1 缝翼降噪方法汇总表Table 1 Summary of noise control approaches of slat noise
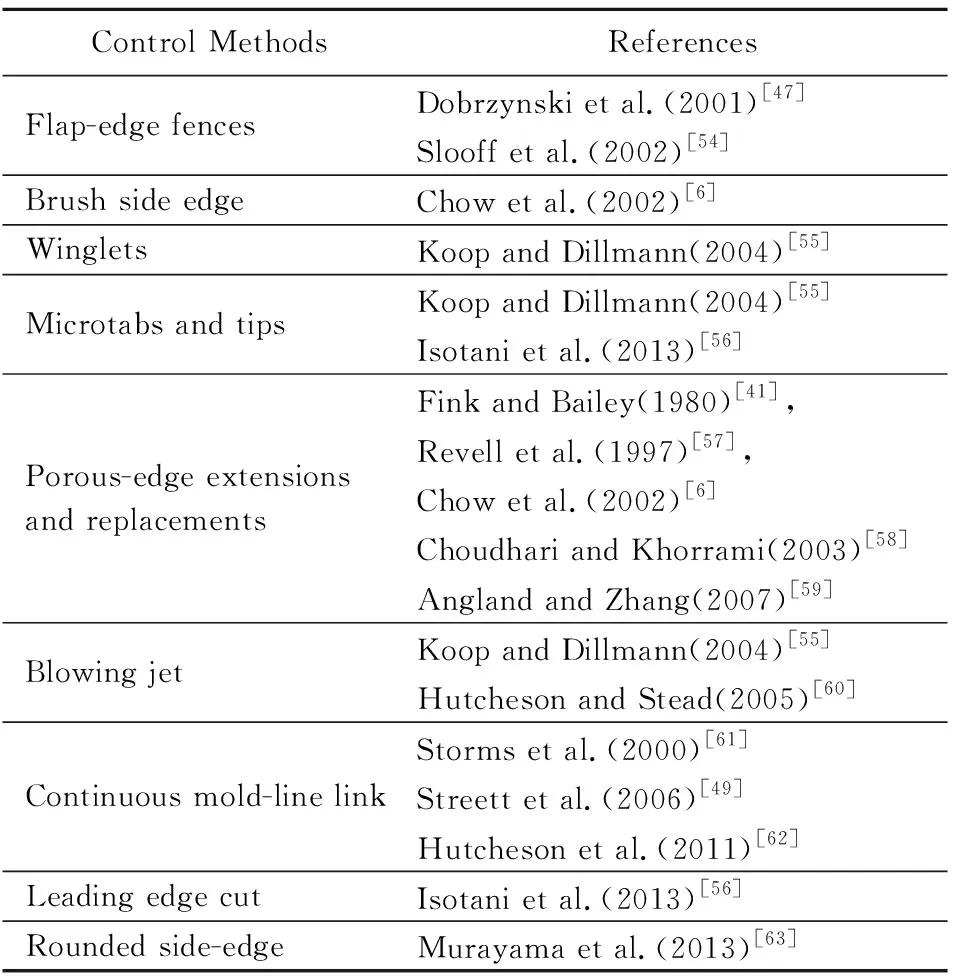
表2 襟翼侧缘降噪方法汇总表Table 2 Summary of noise control approaches of flap noise
缝翼降噪的关键是抑制凹坑区的剪切层不稳定性和减小缝翼尾缘的涡强度,根据噪声控制思想的不同,降噪方法可分为三类:(1) 干扰剪切层技术。利用多孔材料、拌线、涡流发生器、锯齿等方法[5,41-45],干扰剪切层的不稳定性和大涡结构的形成与发展,迫使剪切层中趋于无序状态,缓解剪切层与缝翼壁面的撞击效应,从而达到降低噪声的效果。(2) 整流技术。利用凹坑封盖、凹坑填充、前缘延伸、前缘下垂、长弦缝翼等方法[21,46-51],改变缝翼凹坑区的流动特征,消除或稳定剪切层的震荡,可大幅地降低宽频噪声和低频啸音。(3) 声衬吸声。在缝翼凹坑或主翼前缘布置声衬材料[52-53],进行吸声处理并抑制噪声的近场反射和远场传播。
襟翼降噪的核心是减小翼尖涡的强度和缓解流场的不均匀性,可以通过安装栅栏、毛刷、小翼、微凸起、多孔材料等被动流动控制方法实现[6,41, 47,49,54-59],也可通过喷流等主动流动控制方法完成[55,60]。近年来,连续模线链接和翼尖修整方法取得了较好的降噪效果[49,56,61-63]。Hutcheson等(2011)[62]实验证明连续模线链接方法可降低襟翼侧缘噪声5~17 dB,并且分布于噪声的全部频段。Isotani等(2013)[56]实验得出前缘修型技术可降低侧缘噪声2~3 dB,但该方法对气动力特性有一定影响。
3 增升装置噪声研究的几个难题
3.1 高可靠性的流场/声场一体化研究困难
实验研究方面,虽然非定常流场测量技术(PIV、LDV等)可描述湍流及涡系结构的演化过程,但不能准确测量压力脉动的时空分布与传播过程。数值计算方面,雷诺平均数值计算的时间滤波思想与噪声的时空非定常物理本质相悖,而直接数值模拟(DNS)受制于当前计算资源和数值方法的发展程度,代价昂贵。
大涡模拟是当前开展高可靠性的流场/声场一体化研究最具潜力的研究手段之一。大涡模拟利用亚格子应力模型模化湍流中耗散占优、动量不重要的小尺度涡结构,只求解网格尺度、动量关键的大涡结构,结合高精度数值格式和简化的物理模型,可较好地平衡计算代价与计算精度之间的矛盾,准确描述缝翼流场特征和噪声特性,从而实现高可靠性的流场/声场一体化研究。
3.2 噪声产生机理不明,分析方法受限
傅里叶分析和相关性分析是两种常用的流场/声场分析方法,但存在局限。傅里叶分析可获得某一事件在某一频率上等强度空间分布,但不能分析该事件的时空变化规律;相关性分析可获得空间上时间序列的自/互相关系数,是一种时间统计平均方法,存在严重的滤波问题。增升装置噪声是一类非线性、非平稳、多尺度问题,流场与噪声场之间存在较强的耦合与反馈机制,傅里叶分析和相关性分析不能获得流动中某一事件何时出现、强度如何、何时终止等局部时空信息。
近年来,小波分析、本征正交分解(POD)和动态模态分解(DMD)应用于湍流数据的分析与挖掘[73-75],适用于增升装置噪声机理的研究。基于尺度分解的思想,小波分析突破了傅里叶分析的局限,可获得信号的时域和频域信息,适用于非线性、非平稳、多尺度的信号分析,该方法已在非均匀湍流、喷流噪声等问题中得到应用。本征正交分解是一种数据降维方法,基于最小二乘思想进行最优低维逼近,可获得复杂流场在一段时间内的本征模态和降阶模型,适用于抽取湍流相干结构、描述大尺度含能涡结构的空间分布规律。动态模态分解是从Koopman定理基础上发展的一种数据分解方法,相较于本征正交分解,动态模态分解包含了时间和空间正交基,能够获得降阶模型在某频率上的相位特征,适用于分析周期性振荡流场及噪声脉动场。利用高精度大涡模拟计算结果,选择合理的数据挖掘方法,或将更加深入的阐述增升装置流动与噪声之间的多尺度时空关联、揭示噪声产生机理。
3.3 实施高效、稳定的噪声控制困难
增升装置噪声控制面临诸多挑战,需要综合考虑气动力、结构强度、降噪效果和工程实现等多方面因素。利用锯齿、多孔材料、涡流发生器等方法,可抑制涡流强度而降低噪声,但存在结构强度、气动力下降等问题;利用凹坑封盖、凹坑填充、延展刀片等方法,可保持缝翼升力系数不变,但面临工程实现困难问题;利用声衬技术难以大幅降低噪声源强度;连续模线链接方法可大幅降低襟翼侧缘噪声,却在工程应用中难以加工实现。
4 缝翼流场/声场一体化研究[64-66]
4.1 计算模型与计算方法
本文独立开展了缝翼和襟翼噪声的研究,以避免增升装置中缝翼噪声与襟翼噪声的交织耦合问题。选用两段缝翼模型,如图9所示,该模型具有良好的噪声实验数据,方便数值计算结果与实验的对比验证。无论是两段翼还是多段翼,认为增升装置噪声机理是相同的。

图9FREQUENZ(Airbus)缝翼模型
Fig.9FREQUENZ(Airbus)slatmodel
来流马赫数为0.16,基于主翼弦长的雷诺数为1.4×106,攻角为13°。大涡模拟计算采用自研发的高可靠性大涡模拟计算平台,如图10所示。采用2700万结构化网格、6阶精度紧致格式、2阶时间隐式积分,开展了缝翼噪声的隐式大涡模拟计算。如图11所示,计算结果与实验结果吻合,中低频噪声与实验结果一致。由于实验中采用人工强制转捩,没有捕获到高频啸音。
4.2 缝翼噪声源识别
利用脉动压力云图对低频噪声声源进行了识别(如图12所示),利用纹影云图对缝翼缝道区的高频啸音声源进行了识别。缝翼的主要噪声源包括:(I)低频缝翼缝道噪声;(II)低频主翼尾缘噪声;(III)高频缝翼尾缘噪声;(IV)高频主翼前缘噪声。其中,噪声(IIIf)为高频缝翼尾缘噪声(III)在缝翼内部的反射所致。
4.3 缝翼噪声机理分析
针对缝翼噪声源识别,重点分析了低频缝翼缝道噪声(I)的产生机理。由于篇幅限制,噪声(II、III、IV)的产生机理可见文献[64]——低频主翼尾缘噪声(II)是由于主翼尾缘周期性脱落大尺度涡结构所致,高频缝翼尾缘噪声(III)是由于缝翼尾缘剪切层中的卡门涡街所致,高频主翼前缘噪声(IV)与主翼前缘边界层转捩具有直接关联。
4.3.1 流场与声场的相平均分析
基于压力周期性脉动,进行流场和声场的相平均分析,如图13所示。图13(a)~(d)为涡量云图,图13(e)~(h)为近场压力脉动云图,图13(i)~(l)为中场压力脉动云图。通过相平均分析,可获得低频缝翼缝道噪声(I)的产生机制:缝翼前缘边界层分离而形成剪切层,剪切层中Kelvin-Helmholtz不稳定性放大而形成大尺度相干涡结构(S′及S),含能相干涡结构中的速度梯度与压力梯度守恒,其中涡核附近为低压区,相邻涡核之间为高压区,随着时间推移,相干涡结构撞击缝翼下壁面,速度梯度与压力梯度之间的守恒被破坏,随着涡撞击、涡破碎及涡扩散等效应,在剪切层再附区形成周期性的脉动压力冲击,脉动压力的远场传播而形成低频缝翼缝道噪声。
4.3.2 动态模态分解
利用瞬时流场的脉动压力,开展动态模态分解(DMD)研究。图14为DMD模态的频谱图,频谱图中圆点与低频窄带噪声频率一致,说明能量较高的DMD模态主要处于低频段,峰值频率对应的DMD模态与噪声产生具有直接的关联。提取低频流场振荡所对应的模态,如图15所示。DMD模态是对剪切层中大尺度涡结构的动态分解,反映了在某频率下的非定常大尺度涡结构的空间分布特征,所有频率下DMD模态的加权效应可复原剪切层在一段时间内的非定常特性。通过DMD模态分解,将剪切层中动态模态系数周期性最强的几个模态提取出来。由模态系数频谱及模态空间分布规律表明:在几个特定频率下,缝翼剪切层中大尺度涡结构存在周期性的动态特性,该动态特性与缝翼低频噪声的产生具有直接关联,特定频率下的大尺度涡结构撞击壁面,导致周期性的涡破碎和壁面压力振荡行为,从而由涡撞击区域向外场辐射出与大尺度涡结构动态频率一致的噪声信号。通过DMD分析,可以分离出每个动态模态对压力脉动的贡献,可以对窄带噪声所对应的模态进行分解与描述。
4.3.3 闭环反馈机制
上文明确了缝翼低频窄带尖频噪声来源于剪切层中大涡结构周期性撞击壁面,为进一步证明大涡结构的产生与噪声激励之间存在流-声耦合的闭环反馈机制,定义参数W*为:

(1)
式中:|ω|为涡量绝对值;L为线段a的长度。线段a布置于缝翼前缘尖点附近,如图16所示。线段a的长度为0.01Cslat,与缝翼尖点的距离也为0.01Cslat。参数W*表征了缝翼前缘尖点附近的涡量变化,线段a的位置选择对以下分析结果没有本质影响。
图16展示了W*的功率谱密度,虚线表示窄带低频噪声的频率,可见W*的频率与低频噪声频率基本一致,表明缝翼尖点附近剪切层的低频振荡频率及不稳定性与缝翼低频噪声激励有关。剪切层大涡结构与噪声之间存在流-声耦合的闭环反馈机制:缝翼前缘剪切层受噪声激励而形成脱落涡,脱落涡向下游发展最终撞击壁面而产生尖频噪声,尖频噪声传播至缝翼前缘再次激励剪切层,形成周期性的闭环反馈。
4.4 缝翼低频噪声频率预测
根据闭环反馈机制,提出了缝翼低频噪声频率的预测模型:
(2)
其中,αl=Lv/La,Kv=Uv/U∞,Lv为剪切层对流路径的总距离,La为噪声传播径的总距离,Uv为剪切层的对流速度,γv表征了涡撞击与噪声产生之间的相位差,为常数0.25。利用预测模型,对三种攻角下的缝翼低频噪声进行了预测,结果如图17所示,可见预测模型具有较好的预测精度。
4.5 缝道参数化影响
基于大涡模拟的流场/声场一体化研究,研究了缝翼缝道参数变化对噪声强度的影响。如图18所示,平移缝翼尾缘于9个不同位置点,而改变缝翼与主翼之间匹配位置。总声压级强度(压力脉动均方根)分布如图19所示。可见缝翼尾缘在点1-3位置时,各方位角的总声压级最小,而位于3-1位置时,总声压级最大。分析统计流场数据可知,当缝翼尾缘位于1-3位置时,其剪切层再附点更加靠近缝翼内部,且再附点区的速度和湍动能强度最弱;而位于3-1位置时,剪切层再附点趋近于缝翼尾缘尖端,再附点区的速度和湍动能强度最强。对于工程设计而言,在保证气动力满足要求的同时,应尽可能的使缝翼剪切层再附点远离缝翼尾缘尖端,尽可能的减小再附点区域的速度。
4.6 基于前缘喷流的缝翼噪声控制研究
缝翼噪声产生机制是由于缝翼剪切层中大尺度相关涡结构与缝翼壁面的撞击效应导致,为实施有效的降噪方法,应尽量干扰或抑制剪切层中大尺度相干涡结构的生成与发展,减弱缝翼内部存在的流场-声场闭环反馈机制。本文采用了缝翼前缘外侧垂直方向和内侧平行方向喷流的降噪措施,降噪效果如图20和图21所示。结果表明采用缝翼前缘外侧垂直方向喷流方式,具有更好的降噪效果,总声压级可降低4~8 dB,低频窄带噪声可完全被抑制。其降噪机理是垂直喷流干扰了缝翼剪切层中的大尺度相干涡结构的生成,阻碍了低频窄带噪声产生的闭环反馈机制。
5 襟翼尾缘流场/声场一体化研究[67]
5.1 计算模型与计算方法
选用NACA 632-215两段襟翼模型,襟翼下偏角为39°,如图22所示。来流马赫数为0.2,基于主翼弦长的雷诺数为1.0×106,攻角为10°。大涡模拟计算采用自研发的高可靠性大涡模拟计算平台。采用3220万结构化网格、6阶精度紧致格式、2阶时间隐式积分,开展了缝翼噪声的隐式大涡模拟计算。图23展示了三个不同位置点上的压力脉动功率密度谱,图23(a)中进行了网格无关性验证。由图23可知,襟翼尾缘噪声主要由低频窄带噪声(St≈0.48)、高频窄带噪声(St≈38、St≈14.8)和宽频噪声组成,其中低频窄带噪声为作者首次发现,高频窄带噪声(St≈38)源于主翼尾缘脱落涡,高频窄带噪声(St≈14.8)源于主翼前缘边界层转捩,详细的声源识别与机理分析见下。
5.2 襟翼尾缘噪声识别
图24显示了襟翼周围的压力脉动云图。数值计算所得噪声源包括:(I)主翼前缘边界层转捩导致的高频啸音;(II)主翼尾缘脱落涡导致的高频啸音。另外,噪声源还包括图23所示的低频噪声(III),但由于其波长较大(≈2.1C),在可信的计算区域内不能够进行流动显示,下节中将利用本征正交分解对其机理进行分析。
5.3 襟翼尾缘噪声机理分析
5.3.1 高频啸音产生机理
图25显示了主翼前缘吸力面上的摩擦阻力系数与压力脉动均方根分布,图中S和R分别表示边界层的分离点和再附点。由图25可知主翼前缘存在层流分离泡,由于雷诺数在1×106量级,层流分离泡的尺度较小,边界层再附点之后发生涡撞击和不稳定性的非线性增长,最终边界层转捩为湍流状态。在再附点附近,压力脉动均方根急剧增长,说明边界层转捩导致了高频啸音(I)的产生。
采用相平均方法,对主翼尾缘中的非定常流场及声场进行了流场显示,如图26所示。图26(a)~(d)为流向涡量云图,图26(e)~(h)为近场压力脉动云图,图26(i)~(l)为中场压力脉动云图。通过相平均分析,可获得高频啸音(II)的产生机制:由于主翼尾缘上、下表面的速度不均匀,在钝体尾缘尾迹中产生周期性脱落的卡门涡街,卡门涡街的尺度与尾缘厚度可比,且脱涡频率与噪声(II)的频率一致,说明高频噪声(II)的产生与尾缘脱涡具有直接的联系。
5.3.2 基于POD分析的低频噪声产生机理
频谱图23显示了襟翼尾缘噪声包含低频窄带噪声(St≈0.48),其波长约为2.1C,在可信的计算区域内不能对其进行流场显示。分析可能的原因包括:(1) 襟翼凹腔内部存在大尺度的非定常流动,产生类似缝翼凹腔流场-声场之间的闭环反馈机制;(2) 襟翼缝道区存在“吹哨子”现象;(3) 襟翼尾缘存在低频大尺度脱涡现象。我们分别对襟翼凹腔、襟翼缝道和襟翼尾缘附近的流场进行本征正交分解(POD)分析,试图抽离非定常流场中的大尺度含能涡结构。POD分析表明,低频噪声的产生与襟翼尾缘脱涡有关,详细阐述如下。
利用襟翼尾缘附近的瞬时压力脉动,开展POD分析。图27中显示了POD模态的无量纲特征值及其累加值分布,其中第1对模态含能占比24%,为主模态,前10个模态的总能量占比约为80%,可表征主要的含能非定常模态,用于重构流场。图28、图29中显示了前6个POD模态的空间分布及其模态系数的频谱图,其中第1对POD模态为主模态,其空间分布呈现出类卡门涡街形态,其频率为St≈0.48,与低频噪声频率一致。
利用前10个POD模态(含能80%),重构脉动压力场,如图30所示,其中S1和S2表示相邻大尺度涡结构的涡核位置,相邻涡核位置的波长约为0.242C。利用重构的非定常脉动压力场,对S1和S2位置脉动压力进行自相关分析,如图31所示,可见最大时间延迟约为τ=2.1C/a∞,与低频噪声频率吻合。由此可知,在缝翼尾缘下游中,存在周期性的大尺度的涡脱落现象,呈现出类卡门涡街形态,类卡门涡街的非定常演化是低频噪声产生的主要机理。
6 襟翼侧缘噪声初步分析
为减小计算量、避免噪声源之间干扰,襟翼侧缘噪声分析采用了单段NACA0012翼型,重点研究翼型侧缘涡的演化和噪声生成机理,认为襟翼侧缘噪声主要是由于翼尖区域的非定常流动导致,简化的单段NACA0012翼型具有与襟翼侧缘噪声相同的噪声产生机理。
来流马赫数为0.175,基于弦长的雷诺数为1.5×106,攻角为12°。大涡模拟计算采用自研发的高可靠性大涡模拟计算平台,采用4000万结构化网格、6阶精度紧致格式、2阶时间隐式积分,开展了隐式大涡模拟计算。计算结果如图32所示,显示了压力脉动云图和Q等值面图。在有攻角条件下,翼尖处产生两个主涡系,分布于翼端侧缘和翼端上表面,与图6(b)示意图一致,两个主涡系混合干扰于翼型尾缘附近。襟翼侧缘噪声包含尾缘脱涡噪声和侧缘涡混合干扰噪声,由噪声波长可知侧缘涡混合干扰噪声在中高频段。未来工作将对侧缘噪声的产生机理进行更加细致的研究。
7 增升装置噪声研究的几点展望
7.1 增升装置细节部件的噪声特性研究
增升装置噪声机理与降噪方法研究多是在简化模型上开展的,而真实增升装置包含导轨、除冰孔、配合缝隙等细节部件,细节部件的声学性能与声学指标仍不清楚。以缝翼导轨为例,是典型的钝体扰流现象,非定常的涡脱落伴随产生偶极子声源,声源的强度可能会比缝翼内部噪声源的强度还要高。因此,着眼于增升装置细节部件的噪声特性,全面评价增升装置噪声分布情况,是低噪声增升装置设计的开始。
7.2 全机全尺寸增升装置噪声仿真分析
随着计算资源和计算方法的不断发展,可实现对全机全尺寸增升装置噪声的数值仿真。全机全尺寸增升装置噪声仿真考虑了不同噪声源之间的耦合干扰,考虑了横流对噪声特性的影响,考虑了增升装置细节部件的噪声组成。对于工程应用而言,全机全尺寸的噪声仿真数据更具有工程指导价值。
7.3 增升装置噪声与气动力的一体化设计
飞机设计,气动先行。大型客机气动设计完成之后,再去评价气动噪声指标,是一种后补式的设计思路,难以实现低噪声要求。开展噪声与气动力一体化设计,在设计之初建立低噪声设计理念,满足气动力要求的同时评估不同构型的噪声指标,或开展噪声和气动力耦合多目标优化设计工作,是开发高升低噪增升装置的必经之路。
8 结 论
针对大型客机增升装置噪声,本文重点总结了增升装置噪声产生机理及噪声控制方法,明确了当前增升装置噪声研究中存在的几个难题:(1) 高可靠性的流场/声场一体化研究困难;(2) 噪声产生机理不明,分析方法受限;(3) 实施高效、稳定的噪声控制困难。针对增升装置典型部件,分别开展了两段缝翼构型、两段襟翼构型和单段翼翼尖的高可靠性大涡模拟,利用相平均方法、本征正交分解、动态模态分解和相关性分析方法,对缝翼噪声、襟翼尾缘噪声和襟翼侧缘噪声机理进行了深入研究,明确了缝翼低频及高频窄带啸音的产生机理,首次发现了襟翼尾缘低频窄带噪声的存在,并阐述了其产生机理。对未来的增升装置噪声研究进行了展望,着力于研究增升装置细节部件的声学性能,开展全机全尺寸增升装置噪声仿真,实现噪声和气动力一体化设计。
参 考 文 献:
[1]ICAO Environment Trends/Aircraft Noise[M/OL]. http://www.icao.int/environmental-protection/Pages/noise.aspx[2]Dobrzynski W. Almost 40 years of airframe noise research: What did we achieve?[J]. Journal of Aircraft, 2010, 47(2): 353-367.
[3]Zhang X. Airframe noise-high lift device noise[J]. Encyclo-pedia of Aerospace Engineering, 2010(6): 3541-3551.
[4]Guo Y P, Joshi M C. Noise characteristics of aircraft high lift systems[J]. AIAA Journal, 2003, 41(7): 1247-1256.
[5]Dobrzynski W, Nagakura K, Gehlhar B, et al. Airframe noise studies on wings with deployed high-lift devices[R]. AIAA 1998-2337, 1998.
[6]Chow L C, Mau K, Remy H. Landing gears and high lift devices airframe noise research[R]. AIAA 2002-2408, 2002.
[7]Brooks T F, Humphreys Jr W M. Flap-edge aeroacoustic measurements and predictions[J]. Journal of Sound and Vibration, 2003, 261(1): 31-74.
[8]Fleury V, Malbéqui P. Slat noise assessment from airbus A340 flyover phased-array microphone measurements[J]. AIAA Journal, 2013, 51: 1667-1674.
[9]黄华, 李伟鹏, 王福新. 基于前缘平行射流的缝翼噪声控制研究[J]. 空气动力学学报, 2014, 32(6): 854-860.
[10]Wang Y T, Wang G X, Zhang Y L. Numerical study of complex flow over 30P30N multi-element[J]. Acta Aerodynamica Sinica, 2010, 28(1): 99-103. (in Chinese)王运涛, 王光学, 张玉伦. 30P30N多段翼型复杂流场数值模拟技术研究[J]. 空气动力学学报, 2010, 28(1): 99-103.
[11] Liu Z R, Wang F X, Song W B, et al. Far-field aeroacoustic analysis for slat of a two dimensional high-lift configuration[J]. Acta Aerodynamica Sinica, 2012, 30(3): 388-393. (in Chinese)刘志仁, 王福新, 宋文滨, 等. 二维增升装置前缘缝翼的远场噪声分析[J]. 空气动力学学报, 2012, 30(3): 388-393.
[12]卢清华, 陈宝. 基于LES方法的增升装置气动噪声特性分析[J]. 空气动力学学报, 2016, 34(4): 448-455.
[13]陶俊, 孙刚, 徐康乐. 基于人工神经网络的缝翼凹槽填充降噪设计[J]. 空气动力学学报, 2015, 33(4): 515-522.
[14]徐佳敏, 宋文滨. 分区LES/DES混合方法及缝翼三维流场模拟[J]. 空气动力学学报, 2014, 32(5): 668-674.
[15]周国成, 谭啸, 陈宝. 襟翼边缘噪声的端板抑制技术试验研究[J]. 空气动力学学报, 2016, 34(3): 379-385.
[16]Kolb A, Faulhaber P, Drobietz R, et al. Aeroacoustic wind tunnel measurements on a 2D high-lift configuration[R]. AIAA 2007-3447, 2007.
[17]Rossiter J E. Wind tunnel experiments on the flow over rectangular cavities at subsonic and transonic speed[R]. RAE-64037, 1964.
[18]Jenkins L, Khorrami M R, Choudhari M. Characterization of unsteady flow structures near leading-edge slat: Part I: PIV measurements[R]. AIAA 2004-2801, 2004.
[19]König D, Koh S R, Meinke M, et al. Two-step simulation of slat noise[J]. Computers & Fluids, 2010, 39(3): 512-524.
[20]Imamura T, Enomoto S, Yokokawa Y, et al. Three-dimensional unsteady flow computations around a conventional slat of high-lift devices[J]. AIAA Journal, 2008, 46(5): 1044-1053.
[21] Imamura T, Ura H, et al. Designing of slat cove filler as a noise reduction device for leading-edge slat[R]. AIAA 2007-3473, 2007.
[22]Khorrami M R, Singer B A, Berkman M E. Time-accurate simulations and acoustic analysis of slat free shear layer[J]. AIAA Journal, 2002, 40(7): 1284-1291.
[23]Storms B L, Ross J C, Horne W C, et al. An aeroacoustic study of an unswept wing with a three-dimensional high lift system[R]. NASA TM-112222, 1998.
[24]Khorrami M R, Berkman M E, Choudhari M M. Unsteady flow computations of a slat with a blunt trailing edge[J]. AIAA Journal, 2000, 38(11): 2050-2058.
[25]Tam C, Pastouchenko N. Gap tones[J]. AIAA Journal, 2001, 39(8): 1442-1448.
[26]Agarwal A, Morris P. Investigation of the physical mechanisms of tonal sound generation by slats[R]. AIAA 2002-2575, 2002.
[27]Takeda K, Zhang X, Nelson P A. Computational aeroacoustic simulations of leading-edge slat flow[J]. Journal of Sound and Vibration, 2004, 270(3): 559-572.
[28]Makiya S, Inasawa A, Asai M. Vortex shedding and noise radiation from a slat trailing edge[J]. AIAA Journal, 2010, 48(2): 502-509.
[29]Fink M R, Schlinker R H. Airframe noise component interaction studies[R]. AIAA 79-0668, 1979.
[30]McInerny S A, Meecham W C, Soderman P T. Pressure
fluctuations in the tip region of a blunt-tipped airfoil[J]. AIAA Journal, 1990, 28(1): 6-13.
[31] Khorrami M R, Singer B A. Stability analysis for noise source modeling of a part span flap[R]. AIAA 98-2225, 1998.
[32]Radeztsky R H, Singer B A, Khorrami M R. Detailed measurements of a flap side-edge flow field[R]. AIAA 98-0700, 1998.
[33]Khorrami M R, Singer B A, Radeztsky R H. Reynolds-averaged Navier-Stokes computations of a flap-side-edge flow field[J]. AIAA Journal, 1999, 37(1): 14-22.
[34]Dong T, Reddy N, Tam C. Direct numerical simulations of flap side edge noise[R]. AIAA 1999-1803, 1999.
[35]Brooks T F, Humphreys Jr W M. Flap-edge aeroacoustic measurements and predictions[J]. Journal of Sound and Vibration, 2003, 261(1): 31-74.
[36]Guo Y. Flap side edge noise modeling and prediction[J]. Journal of Sound and Vibration, 2013, 332: 3846-3868.
[37]Lockard D P, Lilley G M. The airframe noise reduction challenge[R]. NASA TM 2004-213013, 2004.
[38]Casalino D, Diozzi F, Sannino R, et al. Aircraft noise reduction technologies: A bibliographic review[J]. Aerospace Science and Technology, 2008, (12): 1-17.
[39]Li Y, Wang X, Zhang D. Control strategies for aircraft airframe noise reduction original research article[J]. Chinese Journal of Aeronautics, 2013, 26(2): 249-260.
[40]Dobrzynski W, Ewert R, Pott-Pollenske M, et al. Research at DLR towards airframe noise prediction and reduction[J]. Aerospace Science and Technology, 2008, 12(1): 80-90.
[41] Fink M R, Bailey D A. Model tests of airframe noise reduction concepts[R]. AIAA 1980-0979, 1980.
[42]Mendoza J M, Brooks T F, Humphreys W. Aeroacoustic measurements of a wing/slat model[R]. AIAA 2002-2604, 2002.
[43]Kopiev V F, Zaitsev M Y, Belyaev I V, et al. Effect of sweep on chevron slat noise[R]. AIAA 2013-2063, 2013.
[44]Chappell S, Cai Z, Zhang X, et al. Slat noise feedback control with a dielectric barrier discharge plasma actuator[R]. AIAA 2012-2806, 2012.
[45]Chen P, Zhang X, Angland D. Slat noise reduction using a leading edge strip[R]. AIAA 2011-2908, 2011.
[46]Khorrami M R, Lockard D P. Effects of geometrical details on slat noise generation and propagation[J]. International Journal of Aeroacoustics, 2010, 9(4,5): 655-678.
[47]Dobrzynski W, Gehlhar B, Buchholz H. Model and full scale high-lift wing wind tunnel experiments dedicated to airframe noise reduction[J]. Aerosp Sci Tech, 2001, 5(1): 27-33.
[48]Horne W C, James K D, Arledge T K, et al. Measurements of 26%-scale 777 airframe noise in the NASA Ames 40 by 80 Foot Wind Tunnel[R]. AIAA 2005-2810, 2005.
[49]Streett C L, Casper J H, Lockard D P, et al. Aerodynamic noise reduction for high-lift devices on a swept wing model[R]. AIAA 2006-212, 2006.
[50]Wild J, Pott-Pollenske M, Nagel B. An integrated design approach for low noise exposing high-lift devices[R]. AIAA 2006-2843, 2006.
[51] Andreou C, Graham W, Shin H. Aeroacoustic comparison of airfoil leading edge high-lift geometries and supports[R]. AIAA 2007- 230, 2007.
[52]Smith M, Chow L, Molin N. Attenuation of slat trailing edge noise using slat gap acoustic liners[R]. AIAA 2006-2666, 2006.
[53]Ma Z, Zhang X. Numerical investigation of broadband slat noise attenuation with acoustic liner treatment[J]. AIAA Journal, 2009, 47(12): 2812-2820.
[54]Slooff J W, de Wolf W B, van der Wal, et al. Aerodynamic and aero-acoustic effects of flap tip fences[R]. NLR TP 2002-004, 2002.
[55]Koop L, Dillmann A. Reduction of flap side edge noise: passive and active flow control[R]. AIAA 2004-2803, 2004.
[56]Isotani K, Hayama K, Yokokawa Y, et al. An aerodynamic noise reduction study for airframe noise from flap tips[R]. AIAA 2013-2064, 2013.
[57]Revell J D, Kuntz H L, Balena F J, et al. Trailing edge flap noise reduction by porous acoustic treatment[R]. AIAA 97-1646, 1997.
[58]Choudhari M, Khorrami M R. Computational study of porous treatment for altering flap side-edge flowfield[R]. AlAA 2003-31.
[59]Angland D, Zhang X. Measurements of flow around a flap side edge with porous edge treatment[J]. AIAA Journal, 2007, 47(7): 1660-1671.
[60]Hutcheson F V, Stead D J. PIV measurements on a blowing flap[R]. AIAA 2005-212, 2005.
[61] Storms B, Hayes J, Jaeger S, et al. Aeroacoustic study of flap-tip noise reduction using continuous moldline, technology[R]. AIAA 2000-1976, 2000.
[62]Hutcheson F V, Brooks T F, Humphreys Jr W M. Noise radiation from a continuous moldline link flap configuration[J]. International Journal of Aeroacoustics, 2011, 10(5): 565-588.
[63]Murayama M, Yokokawa Y, Imamura T, et al. Numerical investigation on change of airframe noise by flap side-edge shape[R]. AIAA 2013-2067, 2013.
[64]Li W, Liu H. On the mechanism of acoustic resonances in flow past a two-dimensional model-scale leading-edge slat[J]. AIAA Journal, 2017.
[65]Huang H, Li W, Wang F. Slat noise suppression with mass injection[J]. Journal of Aircraft, 2015, 52(1):31-41.
[66]魏佳云, 李伟鹏, 许思为, 等. 基于DMD方法的缝翼低频噪声机理分析[J]. 航空学报, 2018, 39(1): 121469.
[67]Li W, Liu H. Noise generation in flow over a full-span trailing-edge flap[J]. AIAA Journal, 2017, 55: 561-571.
