基于峰值优化的改进PTS算法

季 策, 张 超

(东北大学计算机科学与工程学院, 辽宁 沈阳 110169)

0 引 言

正交频分复用(orthogonal frequency division multiplexing,OFDM)是一种基于多个正交子载波调制的频分复用技术。由于OFDM技术具有抗频率选择性衰落能力强和频谱利用率高等优点,使其在无线局域网、数字视频广播及无线移动通信等领域得到广泛应用[1-2]。然而,OFDM系统中信号的峰均功率比(peak-to-average power ratio,PAPR)较高,当其通过功率放大器时会产生非线性失真,从而导致接收端的误码率(bit error rate, BER)性能下降。所以,如何降低OFDM系统的PAPR已成为研究热点。

对于OFDM系统的高PAPR问题,许多降低PAPR的方法已经被提出,如限幅法[3-5](clipping)、选择映射法[6-10](selected mapping, SLM)和部分传输序列法[11-30](partial transmit sequence, PTS)。其中,SLM和PTS是处理OFDM系统中信号的常用算法,属于概率类的算法,不会产生失真。本文重点研究PTS算法,缺点是计算复杂度较高,计算复杂度主要产生于OFDM系统中备选序列的生成和备选序列的PAPR的计算。为了降低计算复杂度,许多改进的PTS算法相继被提出。文献[11-13]是基于遗传算法的改进PTS算法,通过减少搜索次数,从而降低计算复杂度。文献[14-16]是将PTS算法与限幅法相结合的联合算法,先对OFDM信号作PTS优化处理,再对处理后的信号作限幅处理。文献[17-19]简化了备选序列生成的运算过程,降低了计算复杂度。文献[20-24]是基于峰值优化的PTS算法,峰值优化的思想是对备选序列采样位置的功率值进行分析,对峰值功率较小的采样位置的数据不作处理,而对易出现较大峰值功率的位置的数据集中优化处理,通过减少优化的点数降低计算复杂度。基于峰值优化的PTS算法的核心在于确定易出现较大峰值功率的位置的度量函数,好的度量函数能够准确地确定易出现较大峰值功率的位置,不同的基于峰值优化的PTS算法的区别正是度量函数的不同。

在绝大部分改进的PTS算法中,其基本思路是在PAPR性能和计算复杂度之间进行权衡,通过牺牲部分PAPR性能换取低计算复杂度,或是通过少量增加复杂度来换取PAPR性能的提升。本文提出的改进PTS算法亦是如此,是一种基于峰值优化的PTS算法。文中首先分析了每个采样位置的最大峰值功率出现的特点,然后对其估计得到度量函数Pn,根据度量函数Pn和预设阈值确定易出现较大峰值功率的采样点,对其集中优化,减少了优化的点数,降低了复杂度。本文提出的PTS算法与文献[20]相比,在计算复杂度和BER性能基本相同的情况下,PAPR性能有一定的提升。

1 OFDM系统PAPR

在OFDM系统中,N个经过正交幅度调制(quadrature amplitude modulation,QAM)或正交相移键控(quadrature phase shift keying,QPSK)调制的符号以L倍的过采样产生长度为LN的符号序列X=[X0,X1,…,XLN-1]。其中,Xk(k=0,1,…,N-1)为经过调制的输入符号,Xk(k=N,N+1,…,LN-1)为L倍过采样补的零。频域序列X通过傅里叶逆变换(inverse Fourier transform,IFFT)变换得到OFDM时域序列x=[x0,x1,…,xLN-1],即

(1)

式中,L为过采样因子。

OFDM时域序列x的PAPR定义为

(2)

式中,E[·]表示数学期望。

由于PAPR具有随机性,通常用互补累计分布函数(complementary cumulative distribution function,CCDF)来衡量系统PAPR的统计分布特性,表达式为

CCDF=P(PAPR>PAPR0)=1-(1-e-PAPR0)LN

(3)

式中,PAPR0为阈值。

2 部分传输序列

PTS算法是一种无失真的概率类算法,能够有效地降低OFDM系统的PAPR,其原理如图1所示。在PTS算法中,一个OFDM符号序列X被分割为M个互不相交的子块序列Xm=[Xm,0,Xm,1,…,Xm,LN-1],1≤m≤M。表达式为

(4)

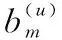
(5)

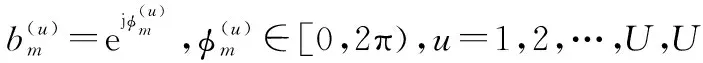
(6)

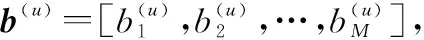
(7)

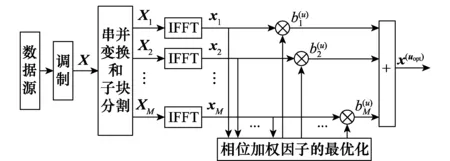
图1 PTS的基本原理Fig.1 Basic principle of the PTS

3 基于峰值优化的PTS算法

基于峰值优化的PTS算法是通过某种度量方法从LN个采样位置中找出易出现较大峰值的Nγ个采样位置,对Nγ个采样位置的采样点数据集中优化而不是对LN个采样位置的采样点数据优化,减少了优化的采样点数,从而降低了计算复杂度。规定度量值Vn(0≤n≤LN-1)为第n个位置的所有备选采样点数据中功率的最大值[22],表达式为

(8)

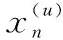
SV(Nγ)为易出现较大峰值功率的采样位置的集合,表达式为

SV(Nγ)={n|Vn≥γ,0≤n≤LN-1}

(9)

式中,γ为预设阈值;Nγ为度量值Vn超过预设阈值γ的采样点个数。然而,计算度量值Vn需计算所有备选采样点数据,显然不可取。

以M=4、W=2为例,即相位因子集合为{1,-1},说明度量值Vn的计算方法。正常情况下,以相位因子1和-1为旋转量的子块采样点数据旋转的图例共WM-1=8种。规定用虚线将坐标复平面均匀分割为2W个区域,虚线分割的区域可以以原点为中心旋转,分如下两种情况讨论:

(1) 如果子块采样点数据分布在虚线分割的对角区域(或同一区域),那么将所有子块采样点数据以相位因子1或-1旋转到第一子块采样点数据x1,n所在区域,所有子块采样点数据求和后平方即为度量值Vn,如图2所示。

(2) 如果子块采样点数据分布在虚线分割的非对角区域(或非同一区域),那么将所有子块采样点数据以相位因子1或-1旋转到包含第一子块采样点数据x1,n的2个相邻区域,每种情况中所有子块采样点数据求和后平方的最大值即为度量值Vn,如图3所示。

图2 对角分布下度量值Vn的计算方法Fig.2 Calculating method of the metric value Vn underdiagonal distribution

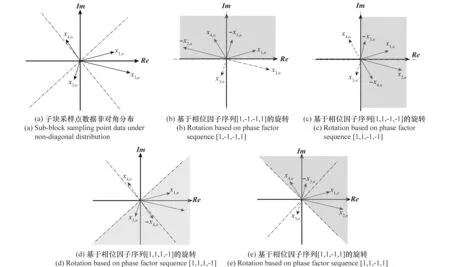
图3 非对角分布下度量值Vn的计算方法Fig.3 Calculating method of the metric value Vn under non-diagonal distribution

虽然上述图示可以直观地得到度量值Vn的计算方法,但是实际操作相当困难,特别是子块采样点数据分布在虚线分割的非对角区域的情况。因为需要对每个采样位置的子块采样点数据的分布进行判断,然后根据分布特性对子块采样点数据进行旋转,该过程非常繁琐,因此需要对上述计算度量值Vn的方法进行简化。基于上述分析,可以发现子块采样点数据分布在对角区域时旋转后的数据占一个区域(阴影),而子块采样点数据分布在非对角区域时旋转后的数据占两个区域(阴影)。如果将所有子块采样点数据旋转到第一子块采样点数据x1,n所在区域(对角分布或非对角分布)使其占一个区域,利用旋转后的子块采样点数据求和后的平方值去估计度量值Vn,那么操作过程将很大程度上得到简化。因此,定义一个新的替代度量值Pn的计算表达式为

(10)

式中,φm,n为子块采样点数据xm,n的相位；|·|为取模运算符;%为取余运算符。规定从坐标复平面的正实轴开始逆时针将复平面均匀分割为2W个区域,若子块采样点数据的分布特性如图4(a)所示,则替代度量值Pn的计算方法如图4(b)所示。由于矢量旋转不改变其模值,所以可以将图4(b)中的所有子块采样点数据旋转到正实轴上方的第一区域,所有子块采样点数据求和后的平方仍为替代度量值Pn,如图4(c)所示。

根据替代度量值Pn与预设阈值γ确定易出现较大峰值位置的集合,即

SP(Nγ)={n|Pn≥γ,0≤n≤LN-1}

(11)

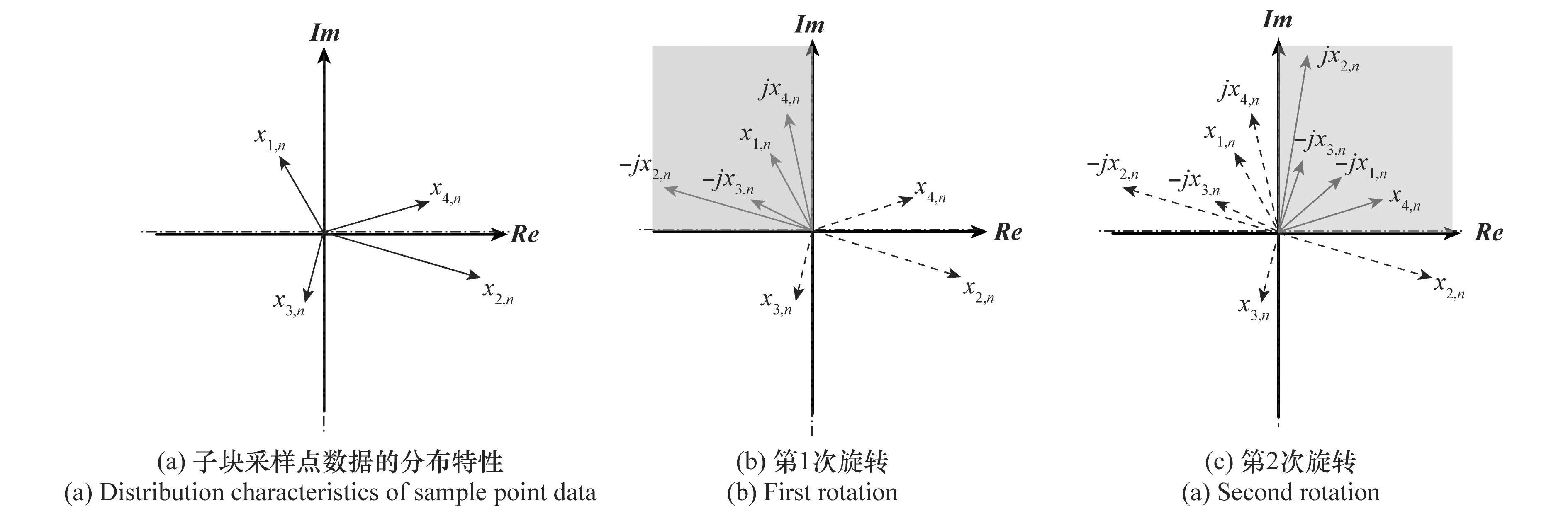
图4 替代度量值Pn的计算方法Fig.4 Calculating method of the alternative metric value Pn

现将基于峰值优化的PTS算法的具体步骤归纳如下:

步骤1将原始数据流经QPSK或QAM调制后的频域序列X分割为M个互不相交的子块序列Xm,对频域子块序列Xm作IFFT变换得到时域子块序列xm;

步骤2计算时域子块序列xm中所有的子块采样点数据xm,n的模值|xm,n|和相位φm,n,根据式(10)计算替代度量值Pn;

步骤3根据替代度量值Pn和预设阈值γ确定易出现较大峰值的采样位置集合SP(Nγ);

步骤4对集合SP(Nγ)中的Nγ个采样位置的数据集中优化,选出最佳相位因子序列的索引uopt;

4 算法的复杂度分析

针对传统PTS算法、文献[20]及本文提出的PTS算法进行计算复杂度分析。其中,文献[20]是一种基于峰值优化的PTS算法。度量函数为

(12)

为了比较本文提出的PTS算法和文献[20]的PTS算法,引入比率pγ,即

(13)

传统PTS算法生成备选序列需要(M-1)ULN次复数乘法和(M-1)ULN次复数加法,计算备选序列的功率需要ULN次复数乘法,选出每个备选序列中最大峰值功率需要U(LN-1)次复数加法,选出PAPR最低的备选序列需要(U-1)次复数加法,共需MULN次复数乘法和(MULN-1)次复数加法。本文提出的PTS算法步骤2中需要(M+1)LN次复数乘法和(M-1)LN次复数加法,步骤3中需要LN次复数加法,步骤4中需要MUpγLN次复数乘法和(MUpγLN-1)次复数加法,步骤5中需要(M-1)LN次复数乘法和(M-1)LN次复数加法,共需(2+pγU)MLN次复数乘法和((2M-1)LN+pγUMLN-1)次复数加法。文献[20]需要((2M-1)LN+pγUMLN)次复数乘法和((2M-1)LN+pγUMLN-1)次复数加法。通常情况下,选用计算复杂度降低率(computational complexity reduction ratio, CCRR)作为衡量计算复杂度降低的标准,即

(14)

传统PTS算法、文献[20]及本文提出的PTS算法的计算量及CCRR如表1所示。其中,N=1 024,L=4,M=8,W=2,pγ=0.073,将文献[20]的PTS算法定义为Q-PTS,本文提出的算法定义为P-PTS算法。

表1 3种PTS算法的计算量及CCRR

由表1中数据可以看出,文献[20]和本文提出的PTS算法的计算量基本相同,这是因为2种PTS算法都是基于峰值优化的,只是度量函数不同。相比传统PTS算法,2种PTS算法计算量大幅度下降约91%。

5 仿真结果

为了说明本文提出的PTS算法在降低PAPR方面的性能,基于Matlab对传统PTS算法、文献[20]的Q-PTS算法及本文提出的P-PTS算法进行了仿真,如图5所示。

仿真参数为:随机分割方式,QPSK调制,子载波数N=1 024,过采样因子L=4,子块数M=8,相位因子个数W=2,pγ=0.073。由图5可知,在pγ=0.073,即采样个数Nγ=300时,本文提出的P-PTS算法的PAPR性能优于文献[20]中的Q-PTS算法。选择pγ=0.073的原因是考虑到整体仿真时间的缘故,随着pγ的增大,图5中P-PTS算法和Q-PTS算法的CCDF曲线逐渐向PTS算法的CCDF曲线靠近,PAPR的性能越好,但仿真的时间越长。

图5 传统PTS、P-PTS、Q-PTS算法的CCDF曲线Fig.5 CCDF curves for the PTS, P-PTS and Q-PTS

图6给出了pγ取不同值时,原始OFDM信号、传统PTS算法和P-PTS算法的CCDF曲线。

图6 pγ取不同值时,原始OFDM信号、传统PTS和P-PTS算法的CCDF曲线 Fig.6 CCDF curves for the original OFDM signal, PTS and P-PTS with the different pγ values

随着pγ的增大,P-PTS算法的PAPR性能越好,计算复杂度越高。图7给出了pγ=0.073时,原始OFDM信号、传统PTS、P-PTS及Q-PTS算法的BER曲线。

图7 pγ=0.073时,原始OFDM信号、传统PTS、P-PTS及Q-PTS算法的BER曲线 Fig.7 BER curves for the original OFDM signal, PTS, P-PTS andQ-PTS when pγ=0.073

由图7可知,原始OFDM信号、传统PTS、P-PTS、Q-PTS算法的BER性能基本相同。

6 结 论

提出了基于峰值优化的PTS算法,该算法权衡了PAPR性能和计算复杂度,通过特定的度量函数Pn确定易出现较大峰值功率点的位置,集中对这些位置上的数据进行优化。通过算法复杂度分析和仿真结果可知,所提出的P-PTS算法相比文献[20]的Q-PTS算法,在同传统PTS算法计算复杂度降低程度和BER性能基本相同的情况下,PAPR性能更优。所以所提出的P-PTS算法具有一定参考价值。

参考文献：

[1] JIANG T, WU Y Y. An overview: peak-to-average power ratio reduction techniques for OFDM signals[J]. IEEE Trans.on Broadcasting, 2008, 54(2): 257-268.

[2] YANG H W. A road to future broadband wireless access: MIMO-OFDM based air interface[J]. IEEE Communications Magazine, 2005, 43(1): 53-60.

[3] SINGH S, KUMAR A. A modified clipping algorithm for reduction of PAPR in OFDM systems[C]∥Proc.of the Computational Intelligence and Computing Research, 2015:1-4.

[4] SINGH R K, FIDELE M. An efficient PAPR reduction scheme for OFDM system using peak windowing and clipping[C]∥Proc.of the Image Information Processing, 2015: 491-495.

[5] ZHU X D, PAN W S, LI H. Simplified approach to optimized iterative clipping and filtering for PAPR reduction of OFDM signals[J]. IEEE Trans.on Communications, 2013, 61(5): 1891-1901.

[6] WOO J Y, JOO H S, KIM K H, et al. PAPR analysis of class-III SLM scheme based on variance of correlation of alternative OFDM signal sequences[J]. IEEE Communication Letters, 2015, 19(6): 989-992.

[7] YANG L, HU W J, SOO K K, et al. Swapped SLM scheme for reducing PAPR of OFDM systems[J]. Electronic Letters, 2014, 50(22): 1608-1609.

[8] WANG L Y, LIU J. Partial phase weighting selected mapping scheme for peak-to-average power ratio reduction in orthogonal frequency division multiplexing system[J]. IET Communications, 2015, 9(2): 147-155.

[9] JI J W, REN G L, ZHANG H N. A semi-blind SLM scheme for PAPR reduction in OFDM systems with low-complexity transceiver[J]. IEEE Trans.on Vehicular Technology, 2015, 64(6): 2698-2703.

[10] JI J W, REN G L. A new modified SLM scheme for wireless OFDM systems without side information[J]. IEEE Signal Processing Letters, 2013, 20(11)： 1090-1093.

[11] LUO R Z, ZHANG C S, NIU N, et al. A low-complexity PTS based on greedy and genetic algorithm for OFDM systems[J]. Chinese Journal of Electronics, 2015, 24(4): 857-861.

[12] KAUR P, SINGH M. Performance analysis of GA-PTS for PAPR reduction in OFDM system[C]∥Proc.of the Wireless Communication, Signal Processing and Networking, 2016: 2076-2079.

[13] SHUKLA J, JOSHI A, BANSAL R, et al. PAPR reduction of OFDM systems using PTS with genetic algorithm at low computational complexity[C]∥Proc.of the Recent Advances and Innovation in Engineering, 2014: 1-6.

[14] ZHAO J H, NI S J, GONG Y. Peak-to-average power ratio reduction of FBMC/OQAM signal using a joint optimization scheme[J]. IEEE Access, 2017, 5(99): 15810-15819.

[15] VERMA R, THARANI L. Constant modulus algorithm for PAPR reduction using PTS and clipping hybrid scheme in MIMO OFDM/A[C]∥Proc.of the Micro-Electronics and Telecommunication Engineering, 2016:337-342.

[16] HUANG X, TAN G W. PAPR reduction method based on improved PTS technology and improved threshold clipping method[J]. Huaqiao University, 2014, 35(5): 492-497.

[17] WANG L Y, YANG X H, WANG Y T. PTS scheme with low complexity IFFTs for PAPR reduction in SISO/MIMO OFDM[C]∥Proc.of the Electronics Information and Emergency Communication, 2013:181-184.

[18] JOSHI A, NIGAM K, BANSAL S. Iterative-grouping and image PTS for PAPR reduction in OFDM system[C]∥Proc.of the Signal Processing and Integrated Networks, 2016: 195-199.

[19] LI E Y, ZOU B J, LIAO H Q. Research on low complexity algorithm of optimum PTS technique[J]. Application Research of Computers, 2012, 29(1): 85-87.

[20] KU S J, WANG C L, CHEN C H. A reduced-complexity PTS-based PAPR reduction scheme for OFDM systems[J]. IEEE Trans.on Wireless Communications, 2010, 9(8): 2455-2460.

[21] CHO Y J, KIM K H, WOO J Y, et al. Low-complexity PTS schemes using dominant time-domain samples in OFDM systems[J]. IEEE Trans.on Broadcasting, 2017, 63(2): 440-445.

[22] LEE K S, CHO Y J, NO J S, et al. A low-complexity PTS scheme using adaptive selection of dominant time-domain samples in OFDM systems[C]∥Proc.of the URSI Asia-Pacific Radio Science Conference, 2016: 1897-1900.

[23] KU S J. Low-complexity PTS-based schemes for papr reduction in SFBC MIMO-OFDM systems[J]. IEEE Trans.on Broadcasting, 2014, 60(4): 650-658.

[24] LEE K S, CHO Y J, WOO J Y, et al. Low-complexity PTS schemes using OFDM signal rotation and pre-exclusion of phase rotation vectors[J].IET Communication,2016,10(5):540-547.

[25] JIANG T, NI C X, GUAN L L, et al. Peak-to-average power ratio reduction in alamouti multi-input-multi-output orthogonal frequency division multiplexing systems without side information using phase offset based-partial transmit sequence scheme[J]. IET Communications, 2014, 8(5): 564-570.

[26] EOM S S, NAM H, KO Y C. Low-complexity PAPR reduction scheme without side information for OFDM systems[J]. IEEE Trans.on Signal Processing, 2012, 60(7): 3657-3669.

[27] JOO H S, KIM K H, NO J S, et al. New PTS schemes for PAPR reduction of OFDM signals without side information[J]. IEEE Trans.on Broadcasting, 2017, 63(3): 562-570.

[28] CHU H X, SHIMAMURA T. A new PTS method for OFDM signals without side information based on constellation reshaping[C]∥Proc.of the Information Science and Systems, 2016：216-221.

[29] KIM K H. On the shift value set of cyclic shifted sequences for PAPR reduction in OFDM systems[J]. IEEE Trans.on Broadcasting, 2016, 62(2): 496-500.

[30] YANG L, SOO K K, LI S Q, et al. PAPR reduction using low complexity PTS to construct of OFDM signals without side information[J]. IEEE Trans.on Broadcasting, 2011, 57(2): 284-290.