大气噪声幅度分布与抑制处理分析
2018-06-28罗忠涛张杨勇
罗忠涛, 卢 鹏, 张杨勇, 张 刚
(1. 重庆邮电大学信号与信息处理重庆市重点实验室, 重庆 400065; 2. 武汉船舶通信研究所低频电磁通信技术实验室, 湖北 武汉 430079)
0 引 言
低频段通信容易受到大气噪声的干扰,导致通信质量与可靠性极大地降低。研究发现,大气噪声由大量的高斯背景下的尖峰脉冲组成,属于非高斯噪声(non-Gauss noise,NGN)[1]。与高斯噪声的信号检测可简化为线性相关器不同,大气噪声中,最佳信号检测的最大似然比检测器难以简化[2]。在实际处理中,大气噪声抑制处理的传统做法是在接收端的匹配滤波器之前加一个非线性处理器,如削波器、置零器[2],将NGN转变成近似高斯噪声处理。不过,这类方法对噪声分布特征的理论研究不足,大多依赖人工经验来选取合适的阈值参数[3]。
大气噪声的统计特性比较复杂,脉冲分量使噪声具有“重尾”特征[4],故学者们提出了多种NGN模型对大气噪声建模[5-8]。目前,常用噪声模型包括对称α稳定(symmetricα-stable, SαS) 模型[5]、Class A/B模型[6]、双参数高斯柯西混合模型[7]及广义高斯分布模型[8]等。各噪声模型的表达形式不同且一般不等价,它们在大气噪声建模中的实用性有待基于实测大气噪声数据的考察。
大气噪声抑制方法的研究也有待实测噪声的验证。大气噪声的抑制一般要求对噪声进行非线性变换[2,9],其客观效果是抑制大幅度脉冲分量[9]。目前人们发展了多种非线性变换技术[10-16]。其中,高斯化处理[10]与局部最优检测处理[11]为2类常用的非线性变换方法,二者均可基于噪声概率密度函数(probability density function, PDF)表达式计算得到。文献[9]介绍了两类方法的系统响应,并通过仿真实验验证了二者的性能。不过,实际中常见噪声模型的PDF表达式计算困难,导致局部最优检测不易应用。为此,提出了模拟局部最优检测的多种非线性变换方法,例如文献[13]提出拟合局部最优检测的系统响应新型非线性变换方法,文献[14]采用设计的非线性变换方法对Class A噪声抑制处理,并分析其处理性能。文献[15]则提出可变步长算法抑制NGN。不过,目前非线性变换技术的研究大多基于仿真数据,尚未得到实测数据的检验。其次,尽管文献通过仿真说明非线性处理有利于提升检测性能[7,9],但二者之间的确切联系尚待深入研究加以理清。
本文主要的创新工作与贡献有如下3点:首先,基于实测大气噪声数据分析其分布概率,验证SαS模型可以很好地描述大气噪声幅度分布。其次,介绍常用非线性处理技术,在高斯化处理的基础上提出新的非线性变换方法,并用实测数据验证其有效性。最后,对实测数据通过各种非线性处理的输出数据进行正态性检验和误码率(bit error ratio,BER)仿真,理清二者之间的联系。
1 实测大气噪声特性分析
1.1 大气噪声特性简介
大气噪声的产生比较复杂,主要因素是自然界中的雷暴活动,其次是人为干扰和地球外噪声等[12]。大气噪声在低频段表现尤为明显,会严重制约低频段通信系统工作能力,如水下通信、地质探测等[3]。
研究表明,大气噪声可认为是由许多具有随机相位幅度、形状不固定的脉冲叠加而成,在幅度上存在严重的“重尾”特征,故可归为NGN。为进一步分析低频大气噪声幅度分布,现基于实测数据评估NGN模型的适用性。
1.2 常用大气噪声模型
在NGN模型中,SαS模型和Class A模型是常用的大气噪声模型,能够描述具有不同程度脉冲性的非高斯分布。
(1) SαS分布
位置参数为0的SαS分布应用最为广泛,其特征函数为[12,16]

(1)
式中,α∈(0,2]为特征指数,一般在1~2取值;γ为分散系数。但是,除高斯分布(α=2)和柯西分布(α=1)外,一般SαS分布的PDF均没有封闭的表达式。可通过数值方法,对SαS分布的特征函数取傅里叶逆变换得其PDF[12]。
(2) Class A模型
Class A模型由Middleton通过假设、推导并适当近似得出。考虑噪声带宽比接收机窄,噪声脉冲通过接收机后基本保持原形,其PDF可以表述为[5,17]
(2)
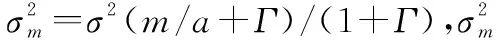
1.3 实测大气噪声分析
本节基于实测噪声数据幅度分布特征验证其非高斯特性,并考察大气噪声模型的实用性。在模型考察中,采用参数化PDF估计方法,分别假设实测噪声服从SαS分布或Class A分布,基于分布参数估计得到在假设分布下的PDF。本文仿真中分别采用了基于样本分位数的SαS模型的参数估计方法[16]和基于样本模值分布的Class A模型的参数估计方法[17]。
本文对多种数据进行处理,将一组典型结果描绘如图1所示。其中,4种不同PDF估计方法分别是:(1)基于核密度估计(kernel density estimation, KDE)[18]的噪声幅度PDF,真实描述实测噪声幅度分布概率;(2)基于SαS模型假设,估计其分布参数再计算在SαS模型下的PDF;(3)基于Class A模型假设,估计其分布参数再计算在Class A模型下的PDF;(4)正态分布假设,估计其均值和方差后计算PDF。图1中实测数据的SαS模型参数估计为α=1.46,γ=0.15;Class A模型参数估计为a=0.29,Γ=0.04;正态分布的均值方差分别为0.004和1.54。
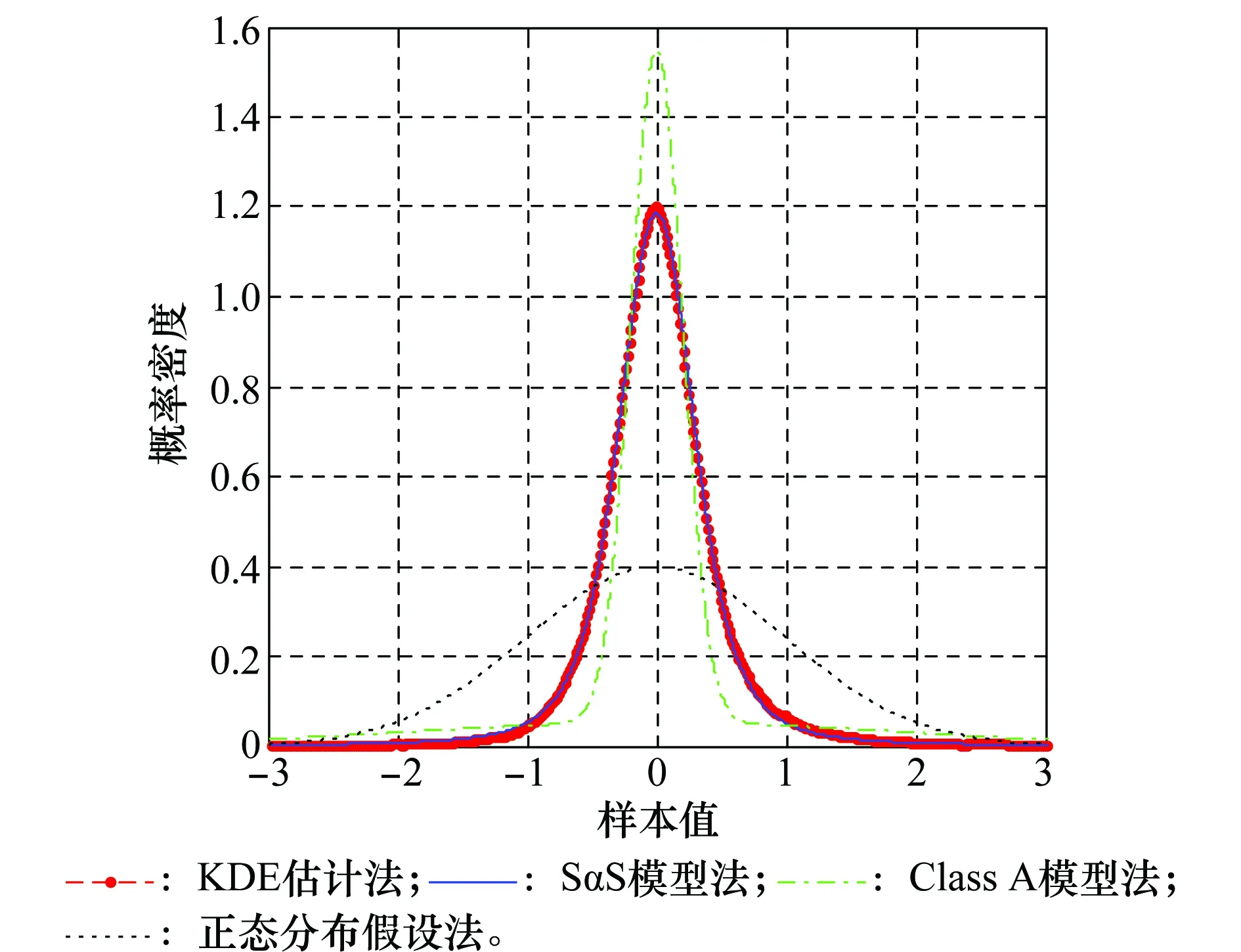
图1 实测数据PDF估计Fig.1 PDF estimates of real data
由图1可见,KDE方法所得噪声幅度PDF与基于SαS模型参数估计PDF的拟合度很高,表明SαS模型适合用于描述实测数据幅度。但是,基于Class A噪声模型获得的PDF与KDE方法相差较大,说明实测数据幅度不服从Class A噪声分布。此外,正态分布PDF比其他PDF的差别非常大,样本分布分散,PDF随样本值增大而下降缓慢。相比之下,实测噪声或非高斯分布的幅度分布概率具有明显的“重尾”特征。
综合上述分析可知,大气噪声数据不服从正态分布,具有脉冲型分布的典型特性;采用中心位置为零的SαS模型,可以很好地描述大气噪声幅度分布概率,而Class A模型的吻合程度差。
2 现有非线性处理技术
大气噪声中的信号处理常采用非线性变换加线性相关器的处理结构,其中关键在于非线性变换方法。目前常用的非线性变换方法有局部最优检测处理[11]、削波处理[2]、置零处理[2]及高斯化处理[10]等。
局部最优检测考虑低信噪比(signal-to-noise ratio,SNR)下的弱信号检测,N次观测下的输出统计量为
(3)
式中,x(n)表示接收信号;s(n)表示发送信号;g(x)=-f′(x)/f(x)表示对接收信号的非线性处理,为零记忆非线性(zero-memory non-linearity, ZMNL)函数,f(·)表示噪声幅度PDF。
考虑到局部最优检测的计算依赖于噪声PDF表达式,而常用的SαS和Class A分布PDF没有封闭表达式,提出类似g(x)功能的非线性处理技术,其中削波处理、置零处理及algebraic-tailed ZMNL (AZMNL)[7]方法具有代表性。削波处理与置零处理常基于经验划定门限,将大于门限的样本点置为零或固定值实现非线性处理。AZMNL则是基于SαS模型PDF分析拟合来确定门限值并采用1/x拖尾的处理方法。
高斯化处理通过NGN PDF计算累积分布函数(cumulative distribution function, CDF),再以高斯分布CDF求逆,实现将NGN转化为高斯分布[9]。这一转化过程是一种非线性变换,虽不来自于局部最优检测,但具有相同的特点,即能够抑制大幅值样本。此外高斯噪声中信号检测结构简单,也是高斯化处理的出发点。
为简化讨论,令F(x)表示标准正态分布CDF,则高斯化函数可表示为
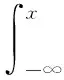
(4)
式中,Q(x)为Q函数。经过高斯化函数的输出服从标准正态分布。
目前,针对高斯化处理的研究还不充足。一方面,缺乏对高斯化后信号检测问题的深入分析;另一方面,噪声正态性与信号检测的联系也没有理清,对于“噪声正态性高意味着更优检测”尚存疑问。后文将深入分析以解决这2个问题。
3 过高斯化非线性处理
现有高斯化处理方法与匹配相关器直接相接,但该方法与局部最优检测存在明显差距[9]。本节研究高斯化处理后的信号检测问题,提出一种新的非线性处理技术。
3.1 高斯化后的信号检测
根据信号检测理论,考虑信号有或无的二元假设下接收信号模型为
(5)
式中,A表示发射信号s(n)的幅度;r(n)表示接收信号;v(n)为独立同分布的噪声。
考虑噪声v(n)为NGN,在检测之前对接收数据进行高斯化处理。设高斯化处理函数为G(x),则2种假设下的高斯化后信号模型为
(6)
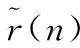
对H1假设下的信号模型做如下变形,即
(7)
考虑低SNR情况下的弱信号检测问题,A值极小,故有r(n)≈v(n),因此H1下信号模型改写为
(8)
式中,G[r(n)]≈G[v(n)]服从高斯分布。
因此,二元假设信号模型式(6)和式(8)下的信号检测问题,转变为在高斯噪声下对确定信号的检测问题,即
(9)
尽管此问题中信号与噪声存在相关性,仍可继续采用匹配滤波理论的最佳检测方法,得到的检测器为
(10)
式中,η表示判决门限。
3.2 一种新的非线性变换
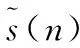
(11)
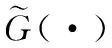
(12)
分析式(11)中检测器结构可见,先对接收信号r(n)进行非线性变换处理,然后再对s(n)匹配滤波处理。这一结构与传统处理如局部最优检测式的结构相同。
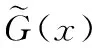
过高斯化处理与高斯化处理、局部最优检测的计算条件是一样的,由噪声幅度分布累计函数计算而来。需要注意,数值计算中为避免零邻域出现异常值,可令函数在零邻域的输出为零。
3.3 过高斯处理的响应分析
本小节考察过高斯化变换的特点,以SαS噪声为例,绘制其非线性变换响应曲线。图2画出了SαS噪声中的局部最优检测、高斯化处理及过高斯化处理的曲线,其中SαS噪声参数α=1.5,γ=1,并令±10-4内的过高斯化处理输出为零。
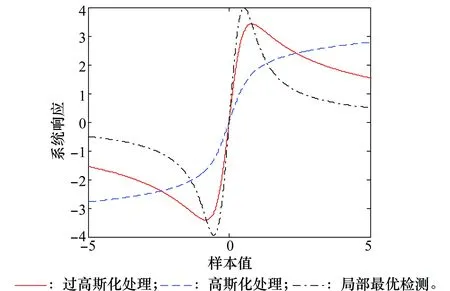
图2 过高斯化处理与非线性处理的响应Fig.2 Responses of Over-Gaussianization and other nonlinear processing methods
由图2可见,过高斯化处理采用了区别于传统变换的非线性变换函数。同时,它也具有脉冲噪声分布的非线性变换的共性,包括变化平滑、奇函数、抑制大模值样本点、保持小模值样本点。然后比较差异,局部最优检测为最佳处理,对大样本点抑制能力最强,过高斯化的抑制能力次之,高斯化处理抑制能力最弱。并且,过高斯化函数和局部最优检测均存在正负2个极值点,而高斯化处理不存在极值点,是一个单增函数,因而在脉冲噪声抑制性能上存在缺陷。
过高斯化处理提供了新的非线性变换方法,既保持了传统局部最优检测和高斯化处理中对于中小模值样本点的近似线性处理,又改正了高斯化处理的缺点以达到大模值样本点的有效抑制。从变换曲线上看,过高斯处理具有合理的非高斯噪声抑制能力,第4节将通过仿真验证过高斯处理在通信系统中的性能。
4 仿真分析
本节仿真BER与正态性统计量所采取的思路为:仿真低频通信信号,结合实测大气噪声数据,模拟低频通信接收信号;采用不同非线性处理方法,对所得输出进行解调后统计BER;对非线性变换输出进行正态性检验,考察数据正态性与BER之间的联系。
4.1 BER仿真
本小节以BER作为NGN抑制能力的衡量标准,仿真测试在不同非线性处理方法下的通信系统性能。
大气噪声数据原采样频率为4 096 Hz,减采样为512 Hz,经去工频信号处理后,其幅度服从脉冲噪声特点,如第1.3节中分析。通信信号仿真采用最小频移键控(minimum-shift keying, MSK)调制,采样频率为512 Hz,信息码元时长1秒对应采样点数为N=512。波形能量为1,通过改变信号幅度A来设置SNR。采用广义信噪比(generalized signal-to-noise ratio, GSNR)[13],定义为
GSNR=10·lg(A2/γ)
(13)
式中,A为发射信号幅度;γ为实测噪声在SαS分布假设下的分散系数估计值。
假设系统已取得理想同步,仿真采用多种非线性处理技术,统计的BER如图3所示,其中每个统计点为蒙特卡罗仿真1 000次的结果,每次蒙特卡罗仿真批处理MSK码元数为200。
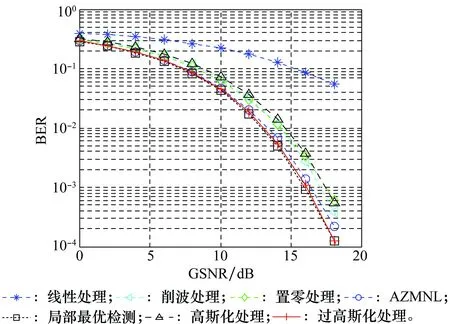
图3 实测大气噪声仿真BER性能曲线Fig.3 Simulated BER performances in real atmospheric noise
由图3可见,各方法的BER均比常规的线性处理更小,其中局部最优检测方法为最优,与理论相符。其次,AZMNL方法由SαS分布PDF分析而设计,与局部最优检测BER曲线相近。削波和置零处理采用概率法10%来设置阈值,与高斯化处理BER曲线均介于局部最优检测与原始数据之间,表明三者均并非最佳处理。
本文提出的过高斯化非线性变换,在图3中取得了与局部最优检测基本相同的BER性能,比原始数据直接检测提高了约8 dB左右。过高斯化处理是在高斯化处理的基础上提出,其BER表现比后者有明显提升。
BER仿真表明,过高斯化的非线性变换具有优良的非高斯噪声抑制能力。针对实测大气噪声而言,过高斯化处理与局部最优检测的性能接近,提供了一种新的大气噪声抑制处理方法。
4.2 正态性检验
非线性处理方法可抑制非高斯分布中模值较大的样本,使得处理后数据客观上更为接近高斯/正态分布。不过,非线性处理输出的正态性的参考价值到底如何,目前人们并无定论。因此,本节将结合正态性检验和BER统计的仿真,来分析和探明二者的联系。
常见的正态性检验技术包括K-S检验和Lilliefors方法[19-20],其中前者要求正态分布参数已知,后者则可在参数未知情况下使用。针对实测噪声,本文仿真利用Lilliefors检验法计算正态检验统计量,判断各种非线性处理后输出数据与正态分布之间的相似程度。
待检噪声包含了实测大气噪声和仿真SαS噪声数据,正态性检验结果如表1所示,其中括号内数值为GSNR=15 dB时BER(四舍五入后)、噪声分散系数γ或其估计均为1。
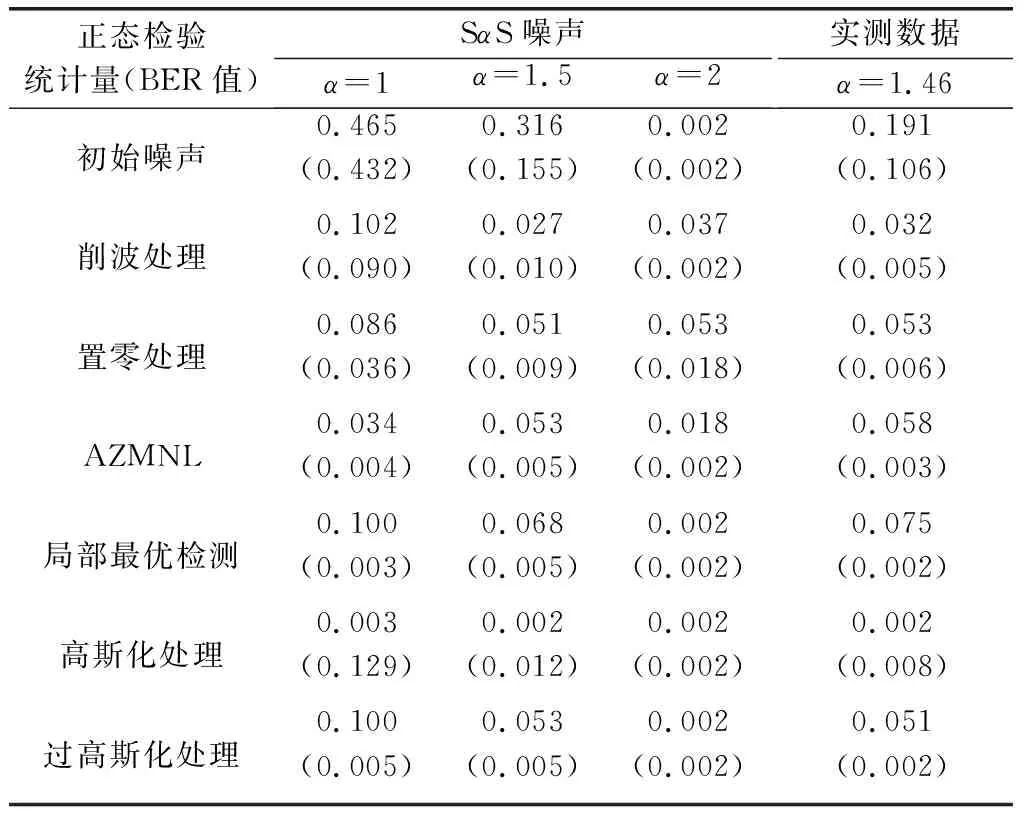
表1 正态检验统计量与BER参照表
首先,观察非线性处理对于正态性的影响。明显,针对α为1或1.5的SαS噪声和实测噪声,各类非线性处理的输出数据均有比原始噪声更低的正态检验统计量。这表明非线性处理确实提高了噪声数据的正态性。
其次,观察正态检验统计量与BER的关系。与第3节仿真结果相同,局部最优检测总是最佳,但是其正态检验统计量并非最小。反之,高斯化处理总是取得很低的正态检验统计量,但是其BER性能并非最优。这说明正态性与BER不存在必然联系。
最后,关注本文提出的过高斯化处理。如前文的推导,过高斯化处理是在高斯化处理基础上的再处理。但如表1所示,相比高斯化处理,过高斯化处理提高了正态检验统计量,取得了BER降低的更佳效果。
由以上仿真分析可知,非线性处理输出数据的正态性提升,是噪声抑制的客观效果而非主观目的,与BER性能优化方向并无必然联系。以提高检测性能的非线性处理,不应以提升正态性为等价或替代性指标。
5 结 论
本文针对低频通信中大气噪声的幅度分布和处理技术展开了研究。首先,基于实测数据的幅值分布分析验证了大气噪声具有非高斯性,采用SαS模型能够较好地拟合其分布。其次,提出了一种新的非线性变换方法——过高斯化处理。在实测噪声仿真处理中,该方法具有与局部最优检测器相近的BER性能。最后,对常见非线性处理方法进行正态性检验和BER仿真,结果表明:正态性提升仅为非线性处理的表象,与噪声抑制和信号检测性能并非正相关。
参考文献:
[1] DAVIS R R, CLAVIER O. Impulsive noise: a brief review[J]. Hearing Research, 2016, 349.
[2] 陈志毅,周穗华,冯士民.脉冲性大气噪声的高斯化滤波[J].数据采集与处理, 2013, 28(6):784-789.
CHEN Z Y, ZHOU S H, FENG S M. Removal of impulsive atmosphere noise based on Gaussian filter[J]. Journal of Data Acquisition and Processing, 2013, 28(6):784-789.
[3] 张杨勇, 刘勇. 低频段大气噪声及处理技术[J]. 舰船科学技术, 2008, 30(b11):85-88.
ZHANG Y Y, LIU Y. Atmospheric-noise at low frequency and its processing technique[J]. Ship Science and Technology, 2008, 30(b11):85-88.
[4] LACHOS V H, ANGOLINI T, ABANTO-VALLE C A. On estimation and local influence analysis for measurement errors models under heavy-tailed distributions[J]. Statistical Papers, 2011, 52(3):567-590.
[5] NIKIAS C L, SHAO M. Signal processing with alpha stable distribution and applications[M]. New York: Wiley, 1995:67-73.
[6] MIDDLETON D. Non-Gaussian noise models in signal processing for telecommunications: new methods an results for class A and class B noise models[J]. IEEE Trans.on Information Theory, 1999, 45(4):1129-1149.
[7] LI X, CHEN P, FAN L, et al. Normalisation-based receiver using BCGM approximation forα-stable noise channels[J]. Electronics Letters, 2013, 49(15):965-967.
[8] HAKIMI S, HODTANI G A. Generalized maximum correntropy detector for non-Gaussian environments[J]. Adaptive Control and Signal Processing, 2018, 32(1):83-97.
[9] 王平波,蔡志明.非高斯数据的高斯化滤波[J].声学与电子工程, 2006, 83(3):26-30.
WANG P B, CAI Z M. Gaussian filtering of non-Gaussian data[J]. Acoustics and electronics engineering, 2006, 83(3):26-30.
[10] 李旭杰,赵鸿燕,杨成胡.α稳定噪声中基于正态变换的次优接收机[J].电路与系统学报, 2012, 17(3):94-97.
LI X J, ZHAO H Y, YANG C H. Normalized transform based sub-optimal receiver inα-stable impulsive environment[J]. Journal of Circuits and Systems, 2012, 17(3):94-97.
[11] LI X T, JIN L W, WANG S Y. A simpli?ed non-Gaussian mixture model for signal LO detection inα-stable interference[C]∥Proc.of the IEEE Congress on Image and Signal Processing, Peking, 2008:403-407.
[12] 邱天爽, 张旭秀,李小兵,等. 统计信号处理——非高斯信号处理及其应用[M]. 北京:电子工业出版社, 2004:139-166.
QIU T S, ZHANG X X, LI X B, et al. Statistical signal processing——non-gaussian signal processing and application[M]. Beijing: Electronic Industry Press, 2004:139-166.
[13] LI X, SUN J, WANG S, et al. Near-optimal detection with constant false alarm ratio in varying impulsive interference[J]. IET Signal Processing, 2013, 7(9):824-832.
[14] OH H, NAM H. Design and performance analysis of nonlinearity preprocessors in an impulsive noise environment[J]. IEEE Trans.on Vehicular Technology,2017,66(1):364-376.
[15] YOO J W, SHIN J, PARK P G. Variable step-size affine projection sign algorithm[J].IEEE Trans.on Circuits and Systems Li-Express Briefs, 2014,61(4):274-278.
[16] BIBALAN M H, AMINDAVAR H. On parameter estimation of symmetric alpha-stable distribution[C]∥Proc.of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2016:4328-4332.
[17] ZABIN S M, POOR H V. Parameter estimation for Middleton class a interference processes[J]. IEEE Trans.on Communications, 1989, 37(10):1042-1051.
[18] SAMIUDDIN M, EL-SAYYAD G M. On nonparametric kernel density estimates[J]. Biometrika, 1990, 77(4):865-874.
[19] AMALE V S, KOLHAR S U, SHASTRIR K, et al. Non-Gaussianity and non-stationarity detection in underwater ambient noise using hypothetical tests[C]∥Proc.of the IAdvances in Signal Processing, 2016:270-275.
[20] CHEN T, CHUANG K S, WU W, et al. Compressed medical image quality determination using the kolmogorov-smirnov test[J]. Current Medical Imaging Reviews, 2017, 13(2):204-209.
