差分进化算法结合正则化解算病态方程

纪元法, 朱亮亮, 孙希延, 严素清

(桂林电子科技大学广西精密导航技术与应用重点实验室, 广西 桂林 541000)

0 引 言

病态问题广泛存在于卫星导航定位等工程测量中。在进行快速定位时,短时间内只能观测到几个历元,使得观测信息不足,导致观测方程病态。通过传统的最小二乘法(least squares, LS)得到的模糊度浮点解与真值相差很大,严重影响定位精度[1]。解决观测方程的病态性是快速提高定位精度的关键。

目前,针对病态问题的解算方法主要分为两类:一类以降低法矩阵的条件数为目标,通过修改法矩阵的奇异值,降低其在求逆过程中对微小扰动的敏感性,从而得到更接近真值的结果。代表性的方法有岭估计[2]、截断奇异值分解法(truncated singular value decomposition,TSVD)[3]和Tikhonov正则化法[4]等;另一类是以遗传算法(genetic algorithm,GA)为代表的智能优化算法,这类方法不试图改善法方程的病态性,而是通过最优化方法得到适应度函数的近似全局最优解,并将其作为病态方程的解[5]。两类方法均存在不同程度的缺陷,前者中的TSVD方法直接舍弃小奇异值,在得到近似解的同时,损害了解估计的分辨率,影响解算效果[6],而岭估计和Tikhonov正则化方法对正则化参数和正则化矩阵选取困难,且带有主观性[7];后者中的GA算法近乎遍历的搜索使优化速度过慢,且参数设置多,不利于实际工程应用[8]。

同时,若观测值存在粗差,将会严重影响定位精度[9],已有的抗差部分岭估计[10]、抗差岭估计[11]等,基于抗差有偏估计的思想,有效地抑制了观测值中的粗差,但解算精度不高。

本文提出差分进化(differential evolution,DE)算法结合Tikhonov正则化的病态方程解算方法。第一,变异过程中自适应地改变缩放因子,即自适应地改变当前个体在下一代新个体中所占的权重,从而在优化的不同时期调节搜索范围与寻优速度之间的关系,提高病态方程解算精度。第二,结合Tikhonov正则化方法,将正则化项加入目标函数中,以减轻病态性,抑制噪声和观测误差带来的粗差影响[12],提高算法的稳健性。

1 病态方程的数学模型

对于观测方程，即

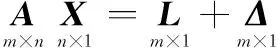
(1)

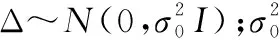
(2)

当观测方程病态时,法矩阵ATA的条件数N很大,对其求逆不稳定,此时若观测向量中存在误差,用最小二乘法直接求解会使误差放大N倍[5],因此得到的结果与真值相差很大。

2 Tikhonov正则化原理

Tikhonov正则化方法是针对不适定问题提出来的[4],病态问题属于不适定问题。对于式(1)的线性化观测模型有

min=‖AX-L‖2+αXTRX

(3)

使式(3)最小化的参数X是所要求的式(1)的Tikhonov正则化解。其中α是正则化参数,R是正则化矩阵,‖·‖2表示2范数。根据Tikhonov估计准则,可以取R=I,即正则化矩阵为单位阵。则式(3)的Tikhonov正则化解为

(4)

由式(4)可知,当正则化矩阵R确定后,Tikhonov正则化的关键是确定正则化参数α。相关学者已做了大量的研究,主要有岭迹法、L-曲线法及直接确定参数法。其中L-曲线法是理论较为严密、也最有可能得到正确正则化参数的方法[1],因此本文选择此方法。

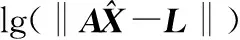
3 自适应加权的DE算法

3.1 基本DE算法原理

DE算法由文献[14]最先提出,具有易用性、寻优速度快、稳健性和强大的全局寻优能力。其具体步骤如下:

步骤1设置种群大小NP、最大迭代次数MaxIter、加权因子F和交叉概率CR等参数,在可行解空间内对初始种群进行随机初始化;

步骤2变异,种群内个体的差分向量经过加权,与种群内相异的个体相加产生当前代变异个体vi,g=xr1,g+F×(xr2,g-xr3,g),其中i≠r1≠r2≠r3;

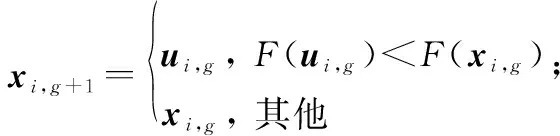
步骤5将种群中保留下来的最优个体作为下一代的初始种群,进入循环迭代过程,重复步骤2～步骤4,直到满足最大迭代次数。

3.2 基本DE算法存在的问题

尽管在非线性优化问题上DE算法具有强稳健性,但它不可避免地存在陷入局部最优解和搜索停滞的问题[15]。若参数设置不当,例如加权因子F和交叉率CR过小,会使算法前期收敛过快,造成整个种群过早汇集于某一局部最优点,此时无论变异个体还是交叉生成的新个体,均与原种群中的个体没有显著差异,这就陷入了局部最优解;当种群没有收敛到极值点且具有多样性时,即使交叉变异后产生了新个体,也找不到比当前种群更优的候选解,造成搜索停滞的问题。自适应加权的DE算法可通过在搜索的不同阶段调节寻优速度与搜索范围的关系,改善陷入局部最优解和搜索停滞的问题。

3.3 自适应加权的DE算法

对于变异式vi,g=xr1,g+F×(xr2,g-xr3,g),更一般地可以写成

vi,g=Ai,g×xr1,g+Fi,g×(xr2,g-xr3,g)

(5)

式中,i和r代表种群中的某个体;g是种群进化代数;Ai,g是对个体xr1,g的加权因子;Fi,g是对差分向量xr2,g-xr3,g的加权因子;Ai,g和Fi,g分别为当前个体和差分向量的权重。较小的Ai,g和较大的Fi,g使算法能在更大范围内探索更多有潜力的解;反之,较大的Ai,g和较小的Fi,g使算法的搜索范围减小,更快地收敛到局部最优解。

基于上述分析,提出自适应改变加权因子Ai,g和Fi,g的DE算法改进形式为

(6)

Fi,g=0.5×(1.5-pi,g)

(7)

式(6)中,i=[1,2,…,NP],NP是种群大小;g是进化代数;ni是第i个个体未更新的次数;max是个体可容许的最大未更新次数。当个体未更新次数达到max时,令Ai,g+1=0.1,从而在下一代的进化过程中强制更新此个体,解决了搜索停滞问题。由于当前个体xr1,g的适应度值越小,其加权因子Ai,g越大,且差分向量xr2,g-xr3,g的加权因子Fi,g越小,根据多次实验得出式(7)中的经验值为0.5和1.5。pi,g的值为

(8)

式中,minF(xg)是第g代中最优个体的适应度值。可以看出,pi,g和加权因子Fi,g都是种群个体适应度值F(xi,g)的函数,加权因子Fi,g的值随着个体适应度值的增大而增大,这是符合逻辑的,因为较大的适应度值,代表了种群中性能较差的个体。当个体性能不佳时,增大的加权因子Fi,g可以使算法在更大范围内搜索潜在的解;而当个体性能较好时,减小的加权因子Fi,g使变异产生的个体与原个体差别减小,算法快速收敛于全局最优解附近的值。通过上述机制,提升DE算法的性能,避免了陷入局部最优解和搜索停滞的问题。

自适应加权的DE算法具体步骤如下:

步骤1设置种群大小NP、最大迭代次数MaxIter、初始加权因子Fi,0、Ai,0和交叉概率CR等参数,在可行解空间内对初始种群进行随机初始化,初始化尽量均匀,使整个种群在可行解范围内均匀分布。

步骤2变异,种群内个体的差分向量经过加权,与相异的个体相加产生当前代的变异个体vi,g=Ai,g×xr1,g+Fi,g×(xr2,g-xr3,g),其中当前代变异个体的当前个体加权因子为

Fi,g=0.5×(1.5-pi,g)

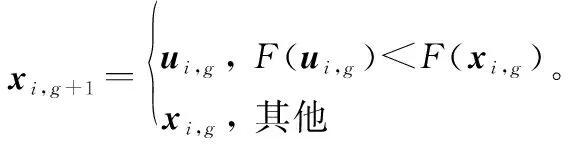
步骤5将种群中保留下来的最优个体作为下一代的初始种群,进入循环迭代过程,重复步骤2～步骤5,直到满足最大迭代次数。

3.4 自适应加权DE算法结合Tikhonov正则化

构造目标函数是DE算法的必要步骤,病态问题中,需要根据误差方程构造目标函数。式(1)写成误差方程的形式为

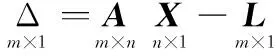
(9)

目标函数可写成如下形式:

minF(X)=(AX-L)T(AX-L)

(10)

将正则化项与目标函数直接相加,得到自适应加权DE算法与Tikhonov正则化相结合的目标函数,即

minF(X)=(AX-L)T(AX-L)+αXTX

(11)

式中,α是正则化参数,用第2节介绍的L-曲线法确定。

4 算例与分析

算例采用文献[1]中的例4.2模拟病态问题,病态方程设计矩阵为

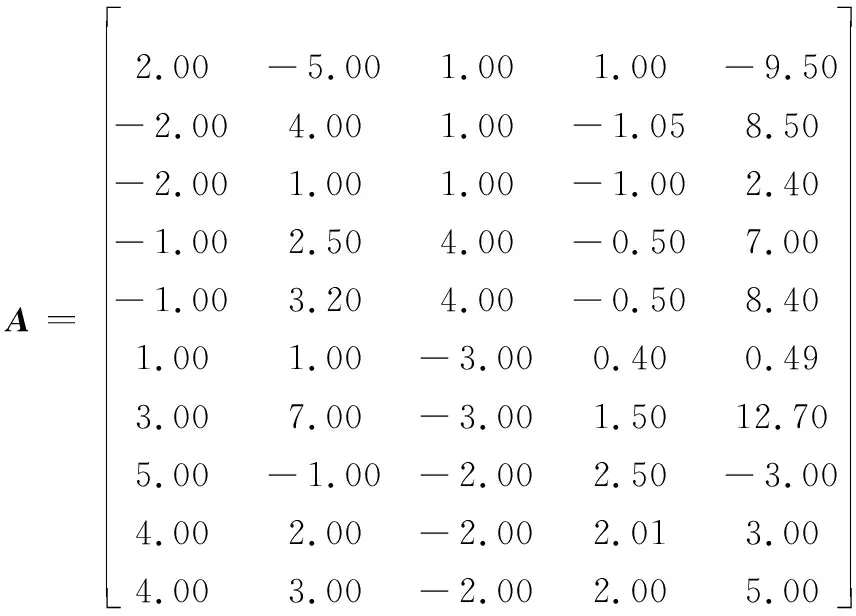
法矩阵N=ATA的条件数为1.289 2×105,方程严重病态,待求向量有5个未知量,真值为Xtrue=[1,1,1,1,1]T,观测噪声Δ～N(0,σ2I),σ=1,根据观测噪声、系数阵A和真值Xtrue,随机数发生器可产生观测向量为

L=[-9.844,10.486,2.249,12.934,14.779,

0.648,21.943,1.892,9.665,12.171]T

设置种群大小NP=20,最大迭代次数MaxIter=500,初始加权因子Ai,g=Fi,g=0.5,交叉概率CR=0.9。待求参数搜索区间设为前3个未知量真值±1,后两个未知量真值±5。式(11)基于误差方程构建了新方法的适应度函数,其正则化参数α由L-曲线法求得,如图1所示。

图1中,曲线上点(0.358 7,0.191 7)处的曲率最大,此点对应的α值为0.3,根据第2节的L-曲线法原理,所求的正则化参数α=0.3。

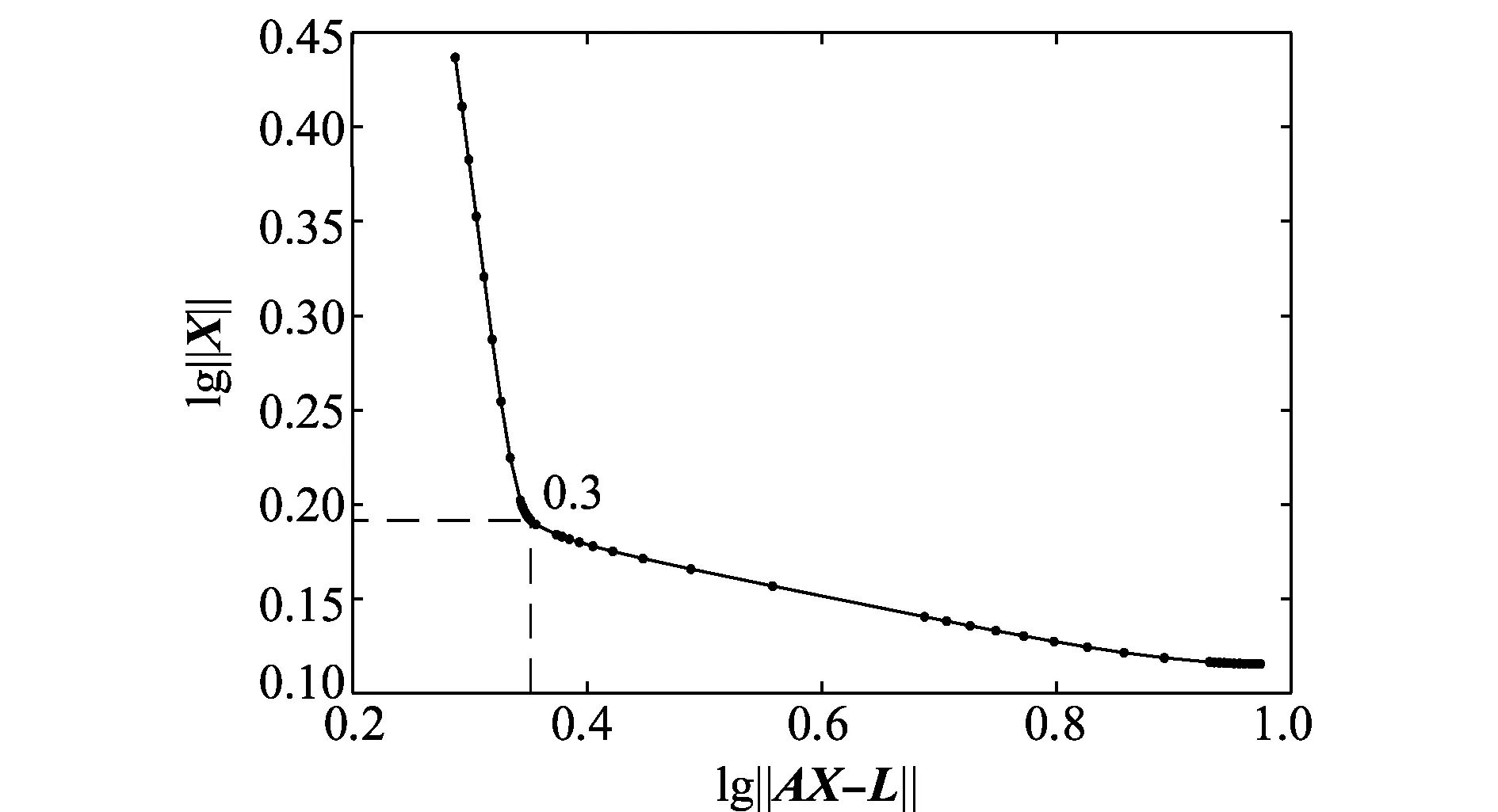
图1 L-曲线法求得的正则化参数Fig.1 Tikhonov parameter by L-curve method

4.1 解算精度分析

由于智能优化算法都是随机搜索算法,不能保证每次搜索结果都相同,因此取100次优化结果的平均值作为新算法的最终结果，即

XmDE=[1.332 2,0.823 5,1.058 7,0.557 4,1.124 2]T

同样利用GA算法对上述算例进行优化,得到100次优化的均值为

Xga=[1.284 3,0.547 0,0.979 3,0.586 9,1.235 8]T

采用LS、TSVD、Tikhonov正则化法和DE算法分别解算本文算例,将欧式范数‖ΔX‖=sqrt((X-Xtrue)T(X-Xtrue))作为解算精度的评价标准,与新算法的结果对比,结果如表1所示。

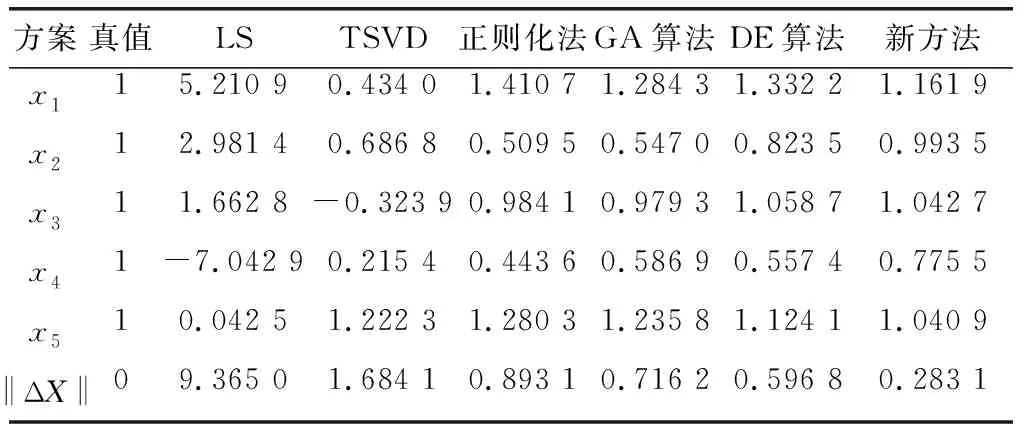
表1 不同方案解算结果对比

根据表1,利用新算法得到的病态方程解的精度最优,与基本DE算法、GA算法、Tikhonov正则化法和TSVD法相比,其解算精度分别高约1倍、1.5倍、2倍和5倍。且LS求解精度最差,严重偏离真实值,这种情况下将不能得到接近真值的位置结果。

4.2 收敛时间分析

在快速定位解算病态方程时,已有的智能优化算法没有考虑运算时间,而快速定位对时间要求严格,是不得不考虑的问题。这里,先以算法的迭代次数为标准,假设每次迭代所用的时间相同,对算法优化过程中的迭代次数进行统计。基于Matlab平台,以第100次优化为例,得到GA算法、基本DE算法及本文所提算法的优化过程如图2所示。

在程序中重新设置各算法的迭代次数,要求比其收敛时间稍大,以满足搜索到最优解的要求。其中,GA算法的迭代次数为350,DE算法为100,新算法为25,分别统计它们的搜索时间,其结果为:新算法约0.122 1 s,DE算法约0.549 2 s,GA算法约1.837 5 s。可见,新算法的收敛时间为基本DE算法的22.23%、GA算法的6.64%。因此,新算法的迭代次数最少,收敛速度最快,更能够满足快速定位中病态问题解算的要求。

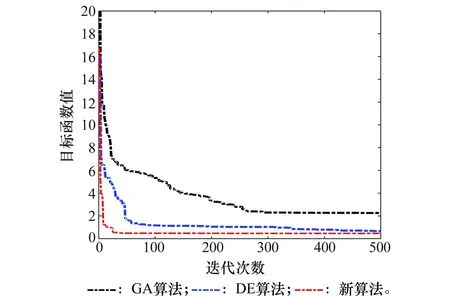
图2 不同算法的优化过程Fig.2 Optimization process of different algorithms

4.3 稳健性分析

为验证新算法解算病态方程的稳健性,在得到的观测向量基础上人为附加部分粗差:第4、5、9、10个观测值上附加20%的粗差,观测向量变为

L1=[-11.813,10.486,2.249,15.514,14.779,

0.648,21.943,2.704,11.599,12.171]T

保持原有参数不变的情况下,重新得到各方案的解算结果如表2所示。

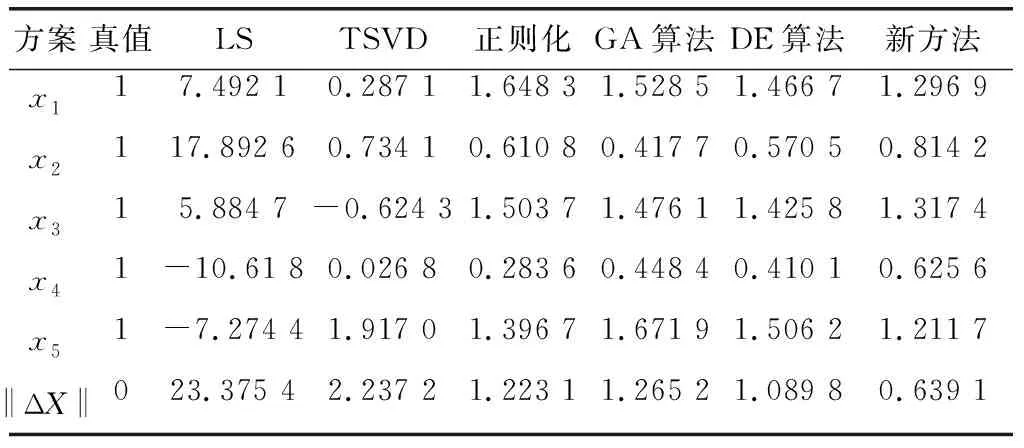
表2 加入粗差后不同方案解算结果对比

对比表2与表1可知,加入粗差后,LS法的解算精度严重降低,TSVD法、GA法和DE法的解算精度均明显降低,其‖ΔX‖值分别增加约0.55、0.54和0.49,新方法的解算精度仍保持最高,‖ΔX‖值增加约0.35。因此,新算法可在一定程度上克服粗差的影响,具有较好的稳健性。

5 结 论

本文在基本DE算法的基础上,提出自适应加权DE算法结合Tikhonov正则化解算病态问题的方法。通过仿真分析,无论与以降低方程病态性为目的的截断奇异值法和Tikhonov正则化法相比,还是与以GA算法为代表的智能优化算法相比,新算法都具有更高的解算精度;且新算法迭代次数最少,收敛时间最短,易实现快速定位;当观测向量中混入粗差时,新算法的解算精度几乎不变,仍保持最高,具有强稳健性。另外,从算法过程来看,易应用于工程实际。

参考文献：

[1] 王振杰. 大地测量中不适定问题的正则化解法研究[D]. 武汉:中国科学院测量与地球物理研究所, 2003.

WANG Z J. Research on the regularization solutions of ill-posed problems in geodesy[D]. Wuhan: Institute of Measurement and Geophysics, Chinese Academy of Sciences, 2003.

[2] ZHANG Y C, DUCHI J C, WAINWRIGHT M J. Divide and conquer kernel ridge regression: a distributed algorithm with minimax optimal rates[J].Journal of Machine Learning Research, 2013, 30(1):592-617.

[3] BOUHAMIDI A, JBILOU K, REICHEL L, et al. An extrapolated TSVD method for linear discrete ill-posed problems with Kronecker structure[J]. Linear Algebra & Its Applications,2011,434(7): 1677-1688.

[4] LIU C S. A dynamical Tikhonov regularization method for solving nonlinear ill-posed problems[J].Computer Modeling in Engineering & Sciences,2011,76(2): 109-132.

[5] GUO Q Y, HU ZH Q. Application of genetic algorithm to solve ill-posed equations for GPS rapid positioning[J]. Geomatics & Information Science of Wuhan University, 2009, 34(1):32-64.

[6] REICHEL L, RODRIGUEZ G. Old and new parameter choice rules for discrete ill-posed problems[M]. New York: Springer-Verlag, 2013.

[7] FAN Q, ZHANG N. Ill-posed problems robust solution of improved fruit fly optimization algorithm combining with Tikhonov regularization method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(6):670-676.

[8] 马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4):1201-1206.

MA Y J, YUN W X. Research progress of genetic algorithm[J]. Application Research of Computers, 2012, 29(4):1201-1206.

[9] WANG Q X, XU T H, XU G C. Application of combining method of outlier detection and robust estimation to GPS kinematic relative positioning[J]. Geomatics & Information Science of Wuhan University, 2011, 36(4):476-480.

[10] 归庆明,韩松辉,隋立芬,等.抗差部分岭估计及其在GPS快速定位中的应用[J].大地测量与地球动力学,2006,26(2):62-65.

GUI Q M, HAN S H, SUI L F, et al. Robust partial ordinary ridge estimator and its applications in GPS positioning[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 62-65.

[11] MARONNA R A. Robust ridge regression for high-dimensional data[J]. Technometrics, 2011, 53(1):44-53.

[12] HE R, HUANG S X, ZHOU C T, et al. Genetic algorithm with regularization method to retrieve ocean atmosphere duct[J]. Acta Physica Sinica, 2012, 61(4):273-335.

[13] XU Y B, PEI Y, DOND F. An extended L-curve method for choosing a regularization parameter in electrical resistance tomography[J]. Measurement Science & Technology, 2016, 27(11):114002.

[14] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.

[15] ZHANG H F, ZHOU J Z, ZHANG Y C, et al. Short term hydrothermal scheduling using multi-objective differential evolution with three chaotic sequences[J]. International Journal of Electrical Power & Energy Systems, 2013, 47(1): 85-99.