光电效应特性曲线“倒置”问题的分析①
2018-06-28,,,
,,,
(佳木斯大学理学院,黑龙江 佳木斯 154007)
0 引 言
光电效应实验是近代物理学史上的经典实验。1905年爱因斯坦根据普朗克的黑体辐射量子假说基础上大胆提出了“光子”概念,成功地解释了光电效应的所有实验结果,建立了爱因斯坦方程,使人们对光的本质认识有了一个新的飞跃,推动了科学家对量子理论的深入研究[1]。
1 实验原理
金属在一定频率的光照射下使电子逸出金属表面的现象叫做光电效应[2]。当光照射到金属上时,根据爱因斯坦的光量子理论,每一个光子具有的能量为E= hν,电子要么吸收一个光子,要么就一点不吸收。如果一个光子的能量大于电子逸出逸出功,被一个电子吸收,能量的一部分将成为该电子的逸出功W= hν0,另一部分则转换为电子逸出金属表面后的动能,由能量守恒定律得[3]
这就是爱因斯坦光电方程。式中h为普朗克常数,ν为入射光的频率,m为电子质量,υm为电子逸出后的最大速度。在光电效应中,光显示出它的粒子性质,所以这种现象对认识光的本性,具有极其重要的意义。
密立根采用“减速电位法”测定电子的最大初动能,并求出普朗克常数h。
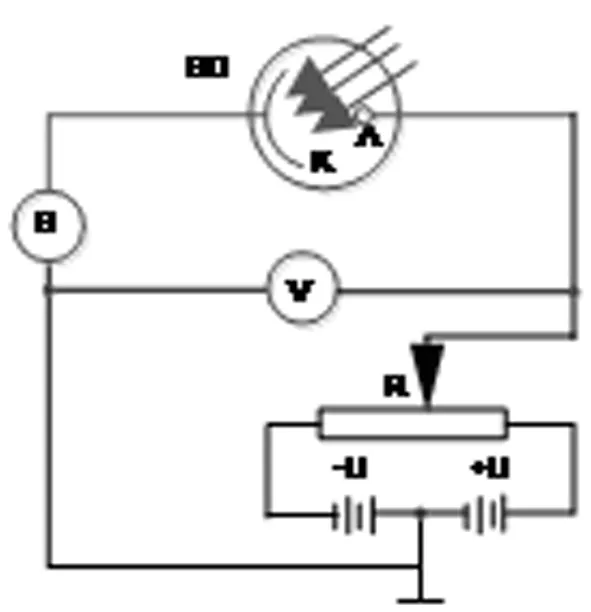
图1 光电效应原理图
实验原理如图1 ,调节电阻R可使光电管的阴极K和阳极A之间获得-U~+U连续变化的电压。当频率为ν的光照到阴极上时,电子从阴极逸出,在电场的作用下向阳极运动,当UAK为正值时,入射的光强越大,形成的光电流也越大,当UAK达到一定值后,光电流饱和不再增加。当UAK为负值时,光电流逐渐减小,直到达到截止电压-U0时,微电流计G的光电流为零,这时电子的最大初动能不能到达阳极K,有
得
由此得到了一种测量普朗克常数的方法,在U0-ν图像中,斜率为h/e,电子电荷e=1.602×10-19C,进而可以求出普朗克常数h。
一般来说,光电效应实验是为高年级学生开设的近代物理实验,随着教学改革的进一步深入,现在绝大多数院校已经把该实验放到面向一年级学生开设的基础物理实验中。在强调物理内涵的同时,也注意提高学生的学习兴趣。利用光电效应实验测量普朗克常量,有助于学生理解光的量子性,更好地认识微观世界普遍存在的波粒二象性和能量交换量子化的规律,以及在近代物理学中的重要地位[3]。实验内容主要包括:测量普朗克常数[4];测量光电管的伏安特性曲线[5];验证饱和光电流与入射光强度成正比。
在实验中,光电管的伏安特性曲线如图2。由图2可以看出:曲线由上到下,是按波长增加的顺序排列的,但曲线L2和L3却是“倒置”的,学生上课时经常问这个问题,想当然认为这“不符合规律”,似乎与“光电流与入射光强度成正比”“相抵触”。现从光谱的强度分布和光电管的光谱响应特性对该问题进行分析。

图2 光电管的伏安特性曲线
2 分 析
低压汞灯的光谱强度分布如图3所示[6],光电管的光谱响应特性曲线如图4所示[7]。
由图3可以看出,谱线λ=435.8nm的发光强度是谱线λ=404.7nm的1.4倍,而从图4可以看出,谱线λ=404.7nm的光谱响应强度仅是谱线λ=435.8nm的是的1.05倍,所以谱线λ=435.8nm的光电流比谱线λ=404.7nm的光电流大,这就是曲线L2和L3 “倒置”的原因。另外曲线L4、L5对应的谱线比谱线λ=404.7nm的发光强度低,并且随着波长的增加光谱响应强度下降较快,所以曲线L4、L5在曲线L2的下面。
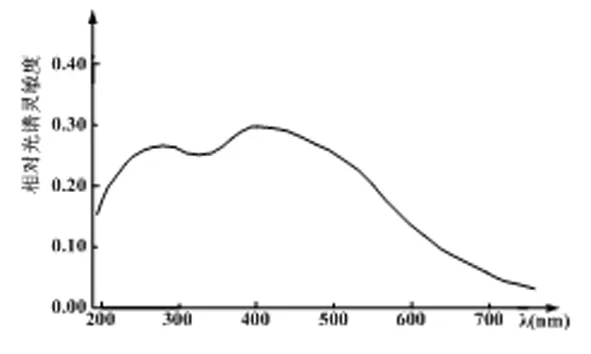
图4 光电管的光谱响应特性曲线
3 结 论
光电效应实验中,光电管产生的光电流不仅与谱线的发光强度有关,还与光电管的光谱灵敏度有关。从光谱强度和光电管的光谱响应特性两方面对光电管的伏安特性曲线L2和L3 “倒置”问题进行了分析,解释了光电特性曲线的分布规律,该规律与“光电流与入射光强度成正比”相符。
参考文献:
[1] 孙晶华.大学物理实验教程[M].哈尔滨:哈尔滨工程大学出版社, 2017.
[2] 姚启钧.光学教程(第3版)[M].北京:高等教育出版社,2002.
[3] 刘景林,王洪涛,芦颖.近代物理实验教程[M].哈尔滨:东北林业出版社,2007.
[4] 吴丽君, 李倩.光电效应测普朗克常数的三种方法[J].大学物理实验, 2007(4):49-52.
[5] 王林香.光电效应伏安特性实验改进研究[J].大学物理实验,2016(1):60-62
[6] 朱鹤年.新概念基础物理实验[M].北京:清华大学出版社,2013.
[7] 李昌厚,范世福,蒋金标,等.光电管和硅光电池的相对光谱响应特性测试方法的研究[J].光学仪器,1995(2):8-12.
