关于粗糙集中的导集拓扑及性质之研究①

(罗定职业技术学院教育系 广东罗定 527200)

0 引 言

1982年的文献[1]中首次提出关于粗糙集的概念。自从1992年以来，国际上许多重要学术会议和研讨班也把粗糙集理论的研究列入会议和讨论班的主要内容之一，这些都极大地促进了该理论的发展及其在各个领域中的应用。从2001年开始国内每年都举办粗糙集与软计算学术会议。粗糙集发展三十多年来，无论是理论研究还是应用研究都取得了很多优秀成果，如粗糙集的近似及相关的数据分析和推理方法与算法、基于数据等价关系的数据分析方法等[2～7]。此外，关于粗糙集的内测度、可能性测度等可测性结构的一些研究见文献[4]。以粗糙集与拓扑为研究背景，主要研究粗糙集与拓扑的一些关系，在此基础上探究粗糙集中的导集拓扑及性质。

1 粗糙集与拓扑空间的关系

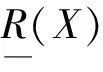
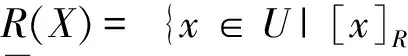
∪{Y∈U/R|Y∩X≠φ}

式中，[x]R={y|(x,y)∈R}是x关于R的等价类，U/R={[x]R|x∈U}是全部R等价类的集合。

定理1[8]设(U,R)是一个Pawlak近似空间，X,Y⊆U是R的可定义集(也就是R的可等价类之并)，(X,Y)是粗糙集的充分必要条件是X⊆Y且(Y-X)∩S=φ。

对任一X∈PS(U)，定义PS(U)到PS(U)的算子：

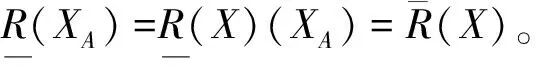
设N={XA,X∈PS(U)}，那么N是U上全体粗糙集的集合。如果X是R的可定义集，那么一定会有XA=X，故有PS(U)⊆N。

定理3[8,9]如果(U,R)是一个Pawlak近似空间，那么N是U上的一个拓扑空间。

证明：(1)显然φ,U∈PS(U)⊆N。

从而XA∩YA∈N。

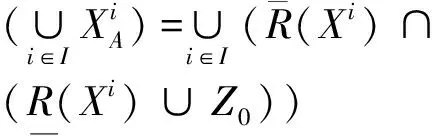
因此

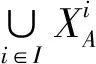
综合上面定理3的证明(1)、(2)、(3)点可知N是U上的一个拓扑空间。

2 粗糙集中的导集运算

为了叙述和计算方便，引入一些符号：令G⊆N，记2G={V|V⊂G}为G的幂集，g在拓扑空间(G,T)中的邻域系为Vg，即Vg={V|V是g的邻域，g∈G,V⊂G}。E在拓扑空间(G,T)中的闭包记为m(E)，E在拓扑空间(G,T)中的导集记为d(E)，即d(A)={g|g是E的聚点，E⊂G}[10]。

定义1[10]假设G为非空集，如果映射m*:2G→2G满足条件：

(1)m*(φ)=φ

(2)E⊂m*(E)

(3)m*(E∪F)=m*(E)∪m*(F)

(4)m*(m*(E))=m*(E)

那么称映射m*:2G→2G为G的闭包运算。

引理1[10]设G为非空集，映射m*:2G→2G为G的闭包运算，那么存在G的唯一拓扑T，使得对任一E⊂G，有式子m(E)=m*(E)成立，其中m(E)是E在拓扑空间(G,T)中的闭包。

引理2[10]若(G,T)为拓扑空间，那么有式子g∈d(E)⟺g∈d(E-{g})g∈m(E-{g})成立。

证明(1)对于任一g∈d(E)，由聚点定义可知，对于任一V∈Vx，必有E∩(E-{g})≠φ成立，于是

E∩((E-{g})-{g})=E∩(E-{g})≠φ成立，故有g∈d(E-{g})。

反之，对于任一g∈d(E-{g})，由聚点定义可知，对于任一V∈Vx，必有E∩((E-{g}))≠φ成立，于是E∩(E-{g})=E∩((E-{g}-{g})≠φ成立，从而有g∈d(E)，所以g∈d(E)⟺g∈d(E-{g})。

(2)对于任一g∈d(E-{g})，由于d(E-{g})⊂m(E-{g})，因而g⊂m(E-{g})。反之，对任一g⊂m(E-{g})，由于m(E-{g})=E-{g}∪d(E-{g})。但是g∉E-{g}，由此可知g∈d(E-{g})。于是g∈d(E-{g})⟺g∈m(E-g)。

3 粗糙集中的导集拓扑

定义2[10]设G为非空集，如果映射d*2G→2G满足条件：对∀E⊆G,F⊆G，有

(1)d*(φ)=φ

(2)d*(E∪F)=d*(E)∪d*(F)

(3)d*(d*(E))=E∪d*(E)

(4)g∈d*(E)⟺g∈d*(E-{g})

那么称映射d*:2G→2G为G的导集运算。

定理4 假设d*为非空集G的导集运算，作映射m*:2G→2G，对于任一E⊂G，做运算定义m*(E)→E∪d*(E)，那么映射m*:2G→2G是G的上的闭包运算。

证明(1)由定义1及其条件(1)，那么有

m*(φ)=φ∪d*(φ)=φ∪φ=φ

(2)根据定义1，m*(E)=E∪d*(E)，从而有E⊂m*(E)。

(3)根据定义1及其条件(2)，那么有

m*(E∪F)=(E∪F)d*(E∪F)=

(E∪F)∪(d*(E)∪d*(F))=

(E∪d*(E))∪(F∪d*(F))=

m*(E)∪m*(F)

从而有m*(E∪F)=m*(E)∪m*(F)。

(4)根据定义1及其条件(2)和(3)，那么有

m*(m*(E))=m*(E∪d*(E))=

(E∪d*(E))∪d*(E∪d*(E))=

(E∪d*(E))∪(d*∪(d*(E)))=

E∪d*(E)=m*(E)

所以，m*(m*(E))=m*(E)。

综合证明，结合闭包运算的定义1便知，映射m*:2G→2G是G上的闭包运算。

定理5 假设d*为非空集G的导集运算，那么存在G的唯一拓扑T，使得对于任一E⊂G,均有d(E)=d*(E)。

证明假设d*为非空集G的导集运算，可以作运算d*:2G→2G，对于任一E⊂G，m*(E)=E∪d*(E)。

根据定理4便知，映射m*:2G→2G是G的一个闭包运算。再根据引理1便知，存在G的唯一拓扑T，使得对于任一E⊂G,均有m(E)=m*(E)。

接下来证明，对于任一E⊂G,均有d(E)=d*(E)。由于在拓扑空间(G,T)中有式子m(E)=E∪d(E)成立，且对于任一E⊂G,均有m(E)=m*(E)，再根据定义1和引理2，对于任一g⊂d(E),均有

g∈m(E-{g})=m*(E-{g})=(E-{g})∪d*(E-{g})

由于g∉E-{g},从而g∈d(E-{g}),根据定义1中的条件(4)，便知g∈d*(E),故有d(E)⊂d*(E)。

对于任一g∈d*(E),根据定义1中的条件4，便有g∈d*(E-{g}),

又因为d*(E-{g})⊂(E-{g})∪d*(E-{g}),

所以有g∈(E-{g})∪d*(E-{g})=m*(E-{g})=m(E-{g}),

于是再根据引理2可以知道，g∈d(E),从而d(E)⊃d*(E)。

综上证明，可得d(E)=d*(E)。

在拓扑空间(G,T)中，若对于任一E⊂G,均有d(E)=d*(E)。于是可得

m(E)=E∪d(E)=E∪d*(E)=m*(E)

因为对于任一E⊂G,均有m(E)=m*(E)的拓扑T是唯一的，那么对于任一E⊂G,均有d(E)=d*(E)拓扑也是唯一的。

4 结 语

根据定理5中的唯一性便知，如果还有其他的拓扑空间(G,T)，使得对于任一E⊂G,均有d(E)=d*(E)，其中d(E)是E在拓扑空间(G,T)中的导集，这说明了一是用开集公理建立的拓扑和用导集运算建立的拓扑是等价的；二是在粗糙集中同样满足导集运算；三是在粗糙集中同样满足拓扑空间闭包运算；四是粗糙集中确实是存在导集拓扑。

参考文献:

[1] Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences, 1982,11:341-356.

[2] Biswas R, Nanda S.Rough Groups and Rough Subgroups[J].Bull Polish Acad Sci Math, 1994,42:251-254.

[3] Iwinski J.Algebraic Approach to Rough Sets[J].Bull Polish Acad Sci Math, 1987,35:673-683.

[4] Kuioki N, Wang P P.The Lower and Upper Approximations in a Fuzzy Group[J].Inform Sci, 1996,90:203-220.

[5] Kuioki N.Rough ideals in Semigroups[J].Inform Sci,1997,100:139-163.

[6] 于敛,程乾生.粗糙集和不可测集[J].科学通报,2000,45:686-688.

[7] 陈德刚,张文修.粗糙集和拓扑空间[J].西安交通大学学报:自然科学版,2001,35:1213-1315.

[8] 熊金城.点集拓扑讲义[M].第3版.北京:高等教育出版社，2003 :16-45.

[9] 乔全喜,秦克云,洪智勇.粗糙集构成的拓扑空间[J].计算机科学，2010，37( 11) :230-231．

[10] 王锋.导集运算与拓扑空间[J].江汉大学学报:自然科学版,2007,35(3):5-6.