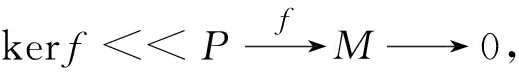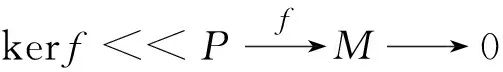关于模的局部直和因子

,

(陇南师范高等专科学校数信学院，甘肃 成县 742500)

0 引 言

Lifting模和Extending模是对偶概念,在环模理论中起着非常重要的作用,近年来引起了许多作者的研究([1][2][3]),文献[4]证明了如下结论:环R是右noetherian环当且仅当每Extending模的局部直和因子是直和因子.文中得到了与之相对偶的结论, 证明了左完全(半完全)环上的任意(有限生成)左R-模的局部直和因子是余闭的.进而,得到了左(或右)artinian环上Lifting模的局部直和因子是直和因子.

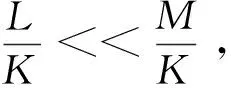
1 本文引理

引理1[1]环R是左完全(半完全)环当且仅当任意(有限生成)投射左R-模是Lifting模.

引理3[3]任意投射Lifting模的直和因子是直和因子.

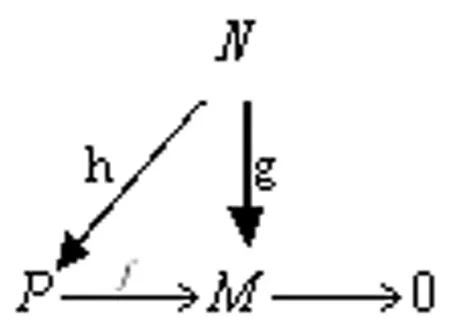
图1

2 主要结论

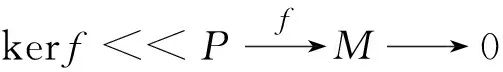
f(Pi+∑j∈FPj)=Mi⊕(∑j∈F⊕Mj)<⊕M

故存在M的直和因子Y,使得M=Mi⊕(∑j∈F⊕Mj)⊕Y.而由P是Lifting模知,存在P的直和因子Q,使得Q≤cf-1(Y),于是f(Q)=Y.从而

P=Pi+∑j∈FPj+Q+kerf=Pi+∑j∈FPj+Q

又因为f(Pi∩(∑j∈FPj+Q))=0,所以Pi∩(∑j∈FPj+Q)⊆kerf<

同理可证Q∩(Pi+∑j∈FPj)<

P=Pi⊕∑j∈FPj⊕Q.从而∑⊕IPi是P的局部直和因子.所以f-1(∑⊕IMi)=∑⊕IPi是P的局部直和因子.

定理5 设R是左完全(半完全)环, 则任意(有限生成)左R-模的局部直和因子是余闭的.

∑⊕IMi=f(∑⊕IPi)≤cM

于是有P=h(N)+kerf=h(N)，即h是满同态,从而可证P是有限生成的.

由定理5,易得出下面结论.

推论6 设R是左完全(半完全)环, 则任意(有限生成) Lifting左R-模的局部直和因子是直和因子.

推论7 设R是左或右artinian环, 则任意提升左R-模的局部直和因子是直和因子.

推论8 设R是半素环,则任意左R-模的局部直和因子是余闭的.

参考文献:

[1] Mohamed Yousif,Ismail Amin,Yasser Ibrahim. D3-Modules[J]. Comm. Algebra, 2014,(42):578-592.

[2] Isao Kikumasa,Yosuke Kuratomi.On H-supplemented modules over a right perfect ring[J]. Comm.Algebra, 2017, (45):1-10.

[3] Yosuke Kuratomi.H-supplemented modules and Generalizations of Quasi-discrect modules [J]. Comm.Algebra, 2016,(44):1-10.

[4] Okado，M. On the decomposition of extending modules[J]. Math.Japonica,1984,(29):939-941.

[5] Yosuke Kuratomi,Chaehoon Chang.Lifting modules over right perfect rings[J]. Comm.Algebra, 2007,(35):3103-3109.

[6] Oshiro,K. Semiperfect modules and quasi-Semiperfect modules[J].Osaka J.Math,1983,(20):337-372.