基于球面三角算法转向臂斜面铣削空间定位探析

， ,

(安徽机电职业技术学院，安徽 芜湖 241000)

0 引 言

随着制造业的不断发展，产品的质量和生产效率成为左右企业生存发展的关键因素。在满足产品精度要求的前提下，生产企业往往通过批量化生产的方式来提高生产效率。然而，在高端机床尚未普及的情况下，对于一些有特殊结构的零部件生产效率的提高就需要柔性化较高的夹具来实现，合理的夹具设计可充分发挥数控机床的潜能，提高加工效率[1]。文中某型汽车转向臂零件结构较为特殊，需设计回转夹具，由于空间工艺角度转换是较为复杂的[2]，球面三角算法确可以很好的解决这类问题。

1 零件图纸分析

某型汽车转向臂零件结构如图1所示，

图1 转向臂零件图

该零件将分别以Φ21mm锥孔及底面和Φ41mm孔及其底面进行定位，铣削夹角为66°的两斜面且两斜面倾角为7°，常规加工手段难以实现，需借助空间转角夹具方能实现，如何实现空间工艺角度的转换和推导定位参数就成为夹具设计的核心问题。

2 定位参数分析及公式推导

根据零件图纸所提供角度建立球面三角如图2所示：

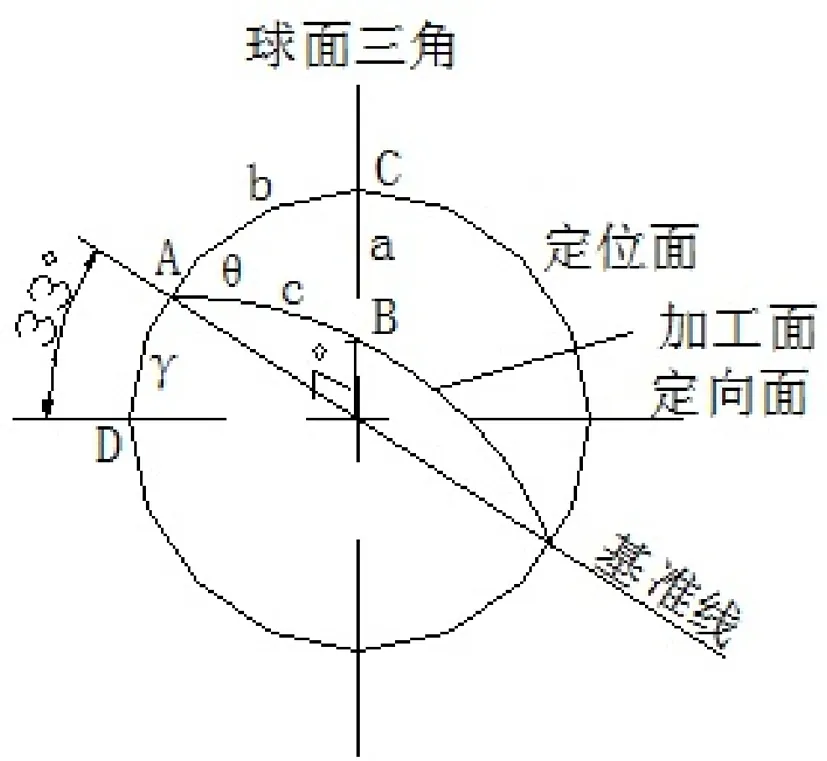
图2 球面三角简图

根据已知条件，在球面三角形△ABC中,因∠C=90°

a=∠C-7°(倾斜角)=83°

(1)

b=∠C-33°(斜面夹角)=57°

(2)

cotA=sinb/tana=0.103

(3)

A=84°7′

由图可知θ=A

为保证铣削效果加工时铣刀与斜面保持垂直，则夹具的扳角=90°-θ=5°53′,定向角(扭角)γ=33°

为方便计算回转轴心位置，建立简图如图3。

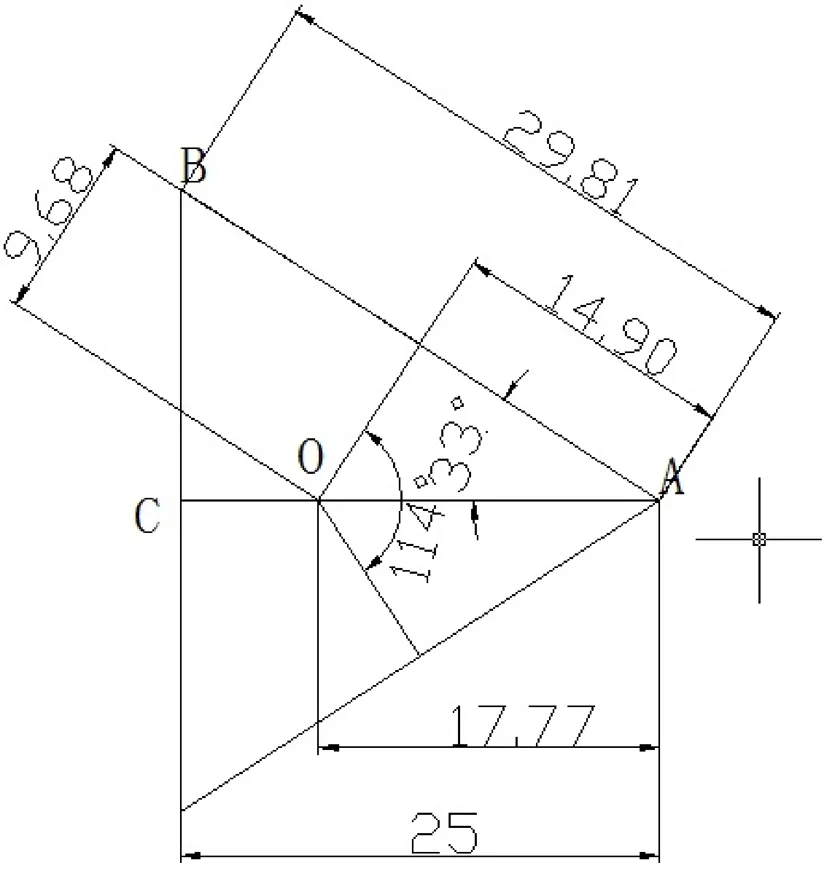
图3 回转中心简图

根据零件图可知AC=25mm，∠BAC=33°

则

AB=AC/cos∠BAC=29.81mm

(4)

又 ∠DAO=∠BAC=33°

按偏差的比例P（Proportional）、积分I（Integral）和微分D（Derivative）进行控制的调节器（简称为PID调节器），它是一种成熟技术的调节器，最广泛应用于连续控制系统。在长期应用中已积累了丰富的经验。随着微机技术的发展，微控制器可以很容易地实现PID控制算法。在模拟调整系统中，PID算法的表达式为：

AD=AB/2=14.905mm

则

AO=AD/cos33°=17.77mm

(5)

DO=AD/tan∠DAO=9.68mm

(6)

根据以上可知Φ21mm定位孔心O1至回转轴心O的距离为87.23mm。

对于回转夹具而言，一般都是采用定位支撑元件绕销孔转动的方式实现回转，为此还需根据扳角和定向角逆向推导出相关定位支撑部件的相关尺寸参数。为此，还需分别建立扳角机构简图(图4)和扭角机构简图(图5)

图4 扳角机构简图

由简图可知，夹具的扳角为5°53′,折合板转起后，O2O3横向距离和O3A直线距离即为支撑件尺寸，推倒如下

已知BC=20mm ∠O2BC=5°53′=∠AO3B

O2B=BC/cosO2BC=20.11mm

(7)

同理 在三角形BO3A中

AB=O2A-O2B=19.89mm

则

O3A=ABcotAO3B=193.02mm

(8)

O3B=AB/sinAO3B=194.04mm

(9)

O3B+O2C=196.1mm

在设计夹具时，选择上述尺寸的支撑件完成组装即可实现所需扳角。同理，可推导出扭角结构相关参数公式，为此建立扭角机构简图如下

图5 扭角机构简图

由简图可知，在三角形AOO4中

AO=BO=AO4cotAOO4=69.29mm

(10)

OO4=OO5=AO4sinAOO4=82.62mm

(11)

在设计夹具时，尺寸AO与OO4可通过选用标准件进行组合实现。

3 结 语

通过利用球面三角算法，将复杂的空间角度问题转化为直观易懂的平面几何问题，并推导出了相关夹具设计尺寸参数方程，为企业后续夹具快捷设计快速组装提供了方案，实现了缩短企业研发周期，提高夹具的使用柔性的目的。

参考文献:

[1] 周太平，康志成，夏翔．数控铣床与加工中心夹具设计[J].现代制造工程2011(2):91-95.

[2] 李奎山,王金福.钻孔加工中转角的球面螺旋计算[J]. 机械工程师,1995(2):19-20.