随机转速波动下水轮机调节系统动力稳定性

许贝贝， 陈帝伊， 张 浩， 李欢欢

(西北农林科技大学 水利水电科学研究院，陕西 杨陵 712100)

水轮机调节系统是水电站系统重要组成部分，其运行状况直接影响水电站系统乃至整个电力系统的稳定与安全运行[1]。因此，从水轮机调节系统角度来探究水电站系统稳定性已经成为一研究热点。水轮机调节系统稳定性研究成果主要体现在以下两方面：①水轮机调节系统线性确定性数学模型[2-3]，该类模型的水轮机力矩往往采用传递函数或者差分形式，此模型主要适用于工况点附近的理论分析；②水轮机调节系统非线性确定性数学模型[4-11]，该类模型的水轮机力矩往往采用由IEEE Group提出的简单非线性公式，此模型能够在一定程度上描述水轮机在过渡过程下的动态力矩特性。

随着风电并网容量的快速增加，使得电网系统随机波动性和难以预测性增强[12]，结合我国水电建设由大型水电站逐渐向巨型机组、特大型水电站系统方向发展的趋势，给水电站系统稳定运行带来了新巨大挑战[13-19]。尤其是受到电力系统随机性增强的影响，机组转速呈现瞬时随机波动现象越加明显[20]。工程经验表明，转速波动过大会破坏水轮发电机组的转矩平衡，从而破坏机组运行的稳定性。因此，考虑转速随机波动引起力矩变化的特性，分析机组运行稳定域的变化规律是非常必要的。

本文基于刚性水击条件下水轮机调节系统模型，考虑转速波动的随机效应，建立了新的水轮机调节系统的随机动力学模型，通过随机逼近理论和非线性系统稳定理论对水轮机调节系统进行稳定性分析，得出了随机激励下系统的随机动力学响应和稳定域的变化规律。

1 随机水轮机调节系统建模

刚性水击条件下水轮机调节系统的动力学模型可表示为

(1)

式中：ωs为发电机转速额定值；Tab为机组惯性时间常数；mt为水轮机力矩；ω为发电机角速度Pe为发电机电磁功率；Dt为水轮机组阻尼系数；eqh和ey为水轮机力矩传递函数；Ty为主接力器时间常数；Tw为压力引水系统水流惯性时间常数；e为中间变量；u为控制信号；y为接力器行程输出。

发电机的转速波动可分为两种类型，如图1所示。第一种是发电机转速在小范围内波动，该范围一般在额定转速的±1%以内，从声音上难以准确判断，其在任意工况下均可能发生，且无规律可循；另外一种转速波动范围变化较大，往往出现在过渡过程中。

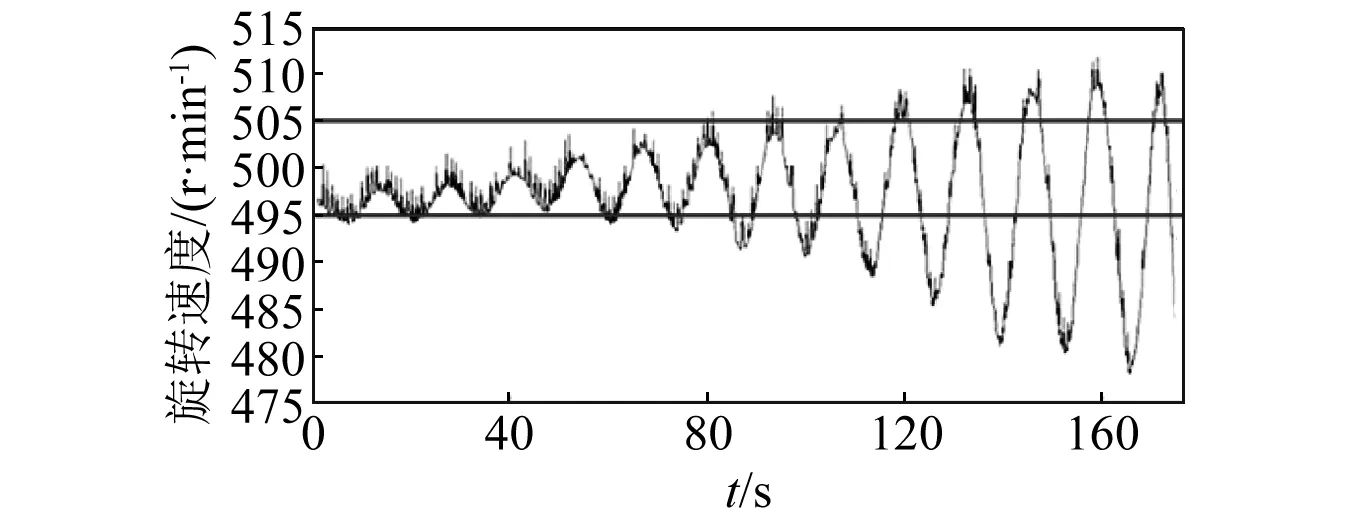
图1 发电机转速波动示意图Fig.1 The diagram of the generator speed fluctuation

针对发电机随机转速波动引起的发电机侧力矩的随机波动，在发电机电磁力矩侧引入随机激励项

(2)

则水轮机调节系统随机动力学模型可表示为

(3)

式中：D为随机强度；u为随机激励项。此处采用文献[21]提出的概率密度函数p(u)

(4)

基于上述提出的概率密度函数p(u)，以Chebyshev多项式为正交基，则随机水轮机调节系统模型动态系数可表示为

(5)

式中：N为Chebyshev多项式的最大个数。

将式(5)代入式(3)，则随机水轮机调节系统数学模型可表示为

(6)

式中：Pe为发电机电磁力矩，其公式可表示为

uPID为控制信号，其公式可表示为

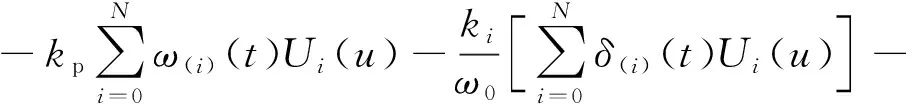
根据文献[18]，可以得到Chebyshev多项式的如下关系表达式

2U0U1=2U1

2U1U2=2(U3+U1)

…

(7)

(8)

当N为某一个值时，式(8)为随机激励项的近似，此处假设ω-1(t)=0和ωN+1(t)=0。将式(8)代入式(6)，两侧乘以Chebyshev多项式Ui(u)(i=0,1,2,3,4)[22]，再分别对等式两边取关于u数学期望，则式(9)可写为

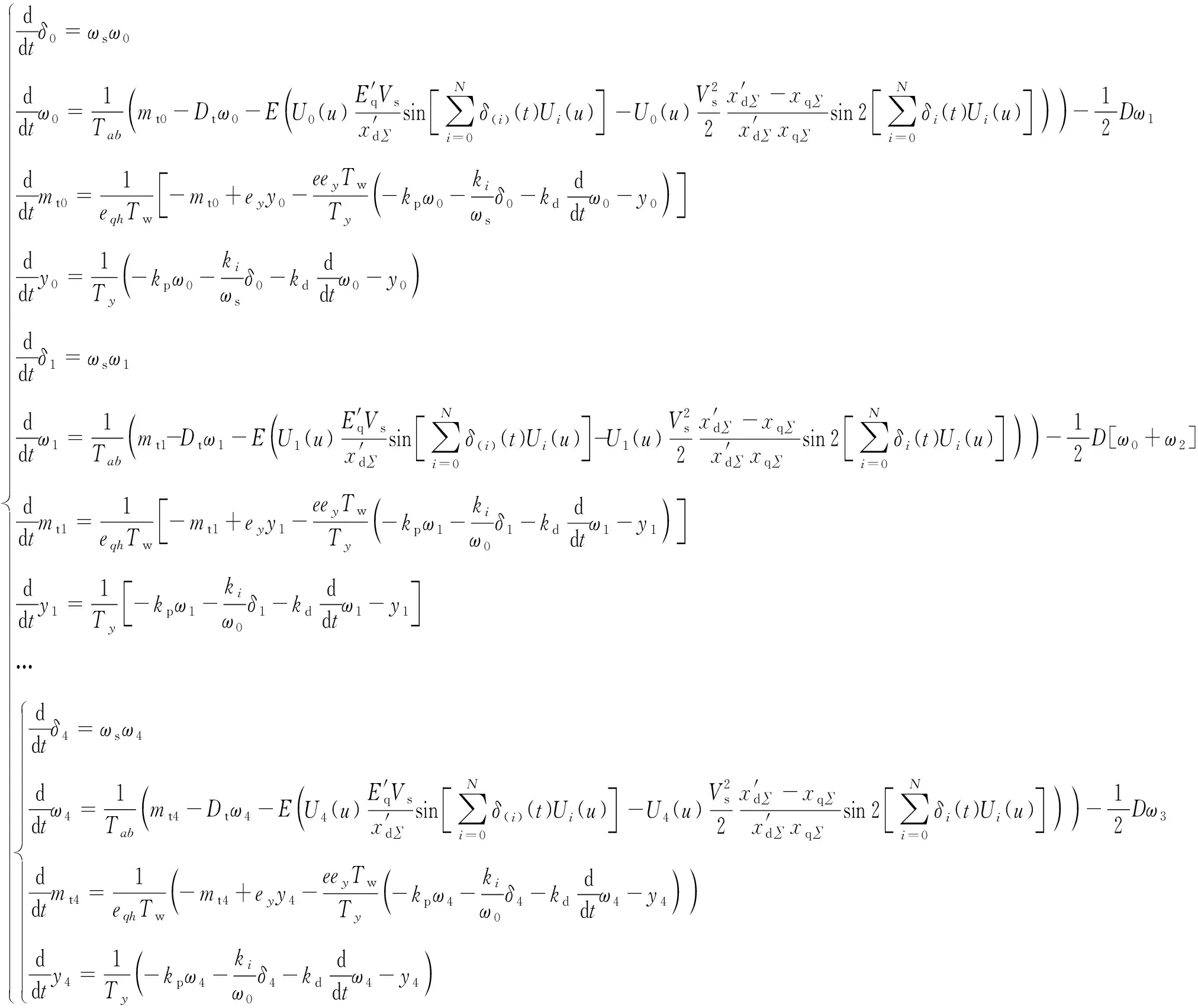
(9)

原随机水轮机调节系统模型的逼近随机响应可表示为

(10)

原随机水轮机调节系统模型的集合平均响应可表示为

(11)

2 随机水轮机调节系统仿真分析

图2展示了随调速器参数kd增大确定性水轮机调节系统式(1)发电机转速ω动态演化过程。由图2可知，随调速器参数kd增大，水轮发电机组共经历四种运行状态：转速ω偏差远大于0的不可调态、转速ω偏差为0时的稳定运行态、转速ω偏差幅值范围(0，0.021 6)的规律振动态和转速ω偏差幅值范围(-0.094,0.171)的随机振动态，即非线性动力学角度的发散态、收敛态、周期一态和混沌态。图3展示了当D=0.02时随调速器参数kd增大随机水轮机调节系统式(10)发电机转速ω动态演化过程。对比图2和图3可发现，确定性系统和随机系统总体动态演化过程具有相似性；但由于随机激励的影响，细节上仍有所区别，具体表现为：

(1)确定性系统式(1)由稳定运行态分别过渡到不可调态和规律振动态的两个关键值，即非线性动力学角度的HOPF分岔点，为0.611和1.833；随机系统式(10)由稳定运行态分别过渡到不可调态和规律振动态的两个关键值为-6.174和-0.097，即随机系统式(10)的两个关键点向左移动；

(2)确定性系统式(1)稳定运行态下，调速器参数kd的可调范围为(0.611，1.833)；随机系统式(10)稳定运行态下，调速器参数kd的可调范围变为(-6.174，-0.097)，即随机系统式(10)在稳定运行态下调速器参数kd可调范围增大；

(3)调速器参数在(-0.097，0.125)内变化时，转速ω变化率很大，机组过渡振动幅值变化十分明显；调速器参数kd=0.125右侧变化时，机组规律振动态类似于确定性系统式(1)机组的运行状态；

(4)确定性系统式(1)由规律振动态过渡到随机振动态的关键值，即非线性动力学角度的混沌分岔点，为5.722，随机系统式(10)状态过渡关键值向左移动，变为4.938。

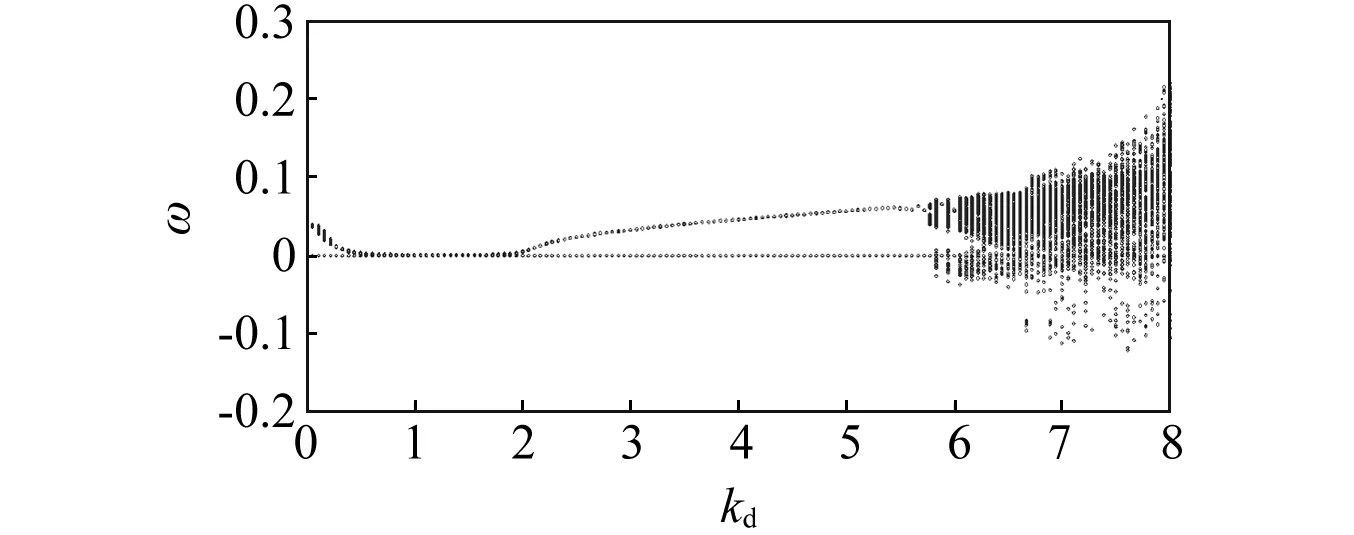
图2 随调速器参数kd增大确定性系统式(1)发电机转速ω动态演化过程Fig.2 Evolution diagram of the fluctuation of generator speed for the deterministic system

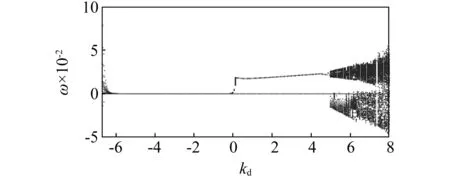
图3 随调速器参数kd增大D=0.02随机系统式(10)发电机转速ω动态演化过程Fig.3 Evolution diagram of the fluctuation of generator speed ω for the stochastic system (10) with D=0.02

图4为D=0.02和kd=3时随机系统与确定性系统发电机角速度ω、接力器行程y时域图和二者的相轨迹图。从图4可知，当调速器参数kd=3和随机强度D=0.02时，确定性系统式(1)和随机系统式(10)均处于规律振动态，但随机系统的发电机角速度ω和接力器行程y振动幅值明显小于确定系统对应参数的振动幅值，随机系统的发电机角速度ω和接力器行程y构成的极限环面积小于确定系统相应极限环的面积。因此，在随机强度D=0.02时，系统所具有的总能量小于确定系统所具有的总能量值，即随机转速波动强度影响水轮发电机组所具有的动态能量值。

图4 调速器参数kd=3随机系统(D=0.02)与确定系统动态过程发电机角速度、接力器行程时域图和相轨迹图Fig.4 Time waveforms of the generator speed, the servomotor displacement, and their phase diagram for the stochastic system with D=0.02 and deterministic system when kd=3

下文将以PID调速器参数kd为自变量，研究不同随机强度下水轮发电机组角速度ω稳定域的变化规律。不同随机强度下调速器参数kd与发电机角速度ω动态演化过程，如图5所示。

图5 以PID调速器参数kd为自变量不同随机强度下发电机转速ω动态演化过程Fig.5 Evolution diagrams of the generator speed of the stochastic system (10) with different levels of intensity D and varying of adjustment coefficient kd

从图5可知，当随机强度D增大时，机组由不可调态过渡到稳定运行态的关键点(命名为关键点1)逐渐向右移动，振幅变化率逐渐变大的不可调态也随关键点1整体向右平移。值得注意的是，在关键点1向右平移过程中，关键点1右侧水轮发电机组运行状态不受随机强度D的影响。因此，调速器参数kd的可调范围是从左向右逐渐缩减的。在随机强度D增大至0.36时，关键点1与机组由稳定运行态过渡到规律振动态的关键点重合，随机系统式(10)的运行状态由不可调态、稳定运行态、规律振动态和随机振动态缩减为不可调态、规律振动态和随机振动态。此时，保证机组稳定运行调速器参数kd的可调范围消失。由于调速器参数kd在(-0.097，0.125)内变化时转速ω偏差变化率很大，因此，当关键点1移动至(-0.097，0.125)时，随机系统式(10)可能会在不可调态和规律振动态交替运行。随着随机强度D继续增大，规律振动态会逐渐消失，保证机组小幅度规律振动调速器参数kd的可调范围也会逐渐消失。当关键点1移动至机组由规律振动态过渡到随机振动态的关键点，随机系统式(10)只保留随机振动态和不可调态。为了更加清晰地观察随机强度D对稳定运行区范围的影响规律，给出不同随机强度下机组稳定域变化，如表1所示。通过上述总结可发现，随机速度波动只对机组关键点1有影响，且随着随机强度D的增大，关键点1及左侧的不可调态不断右移，关键点1右侧机组的运行状态保持不变。

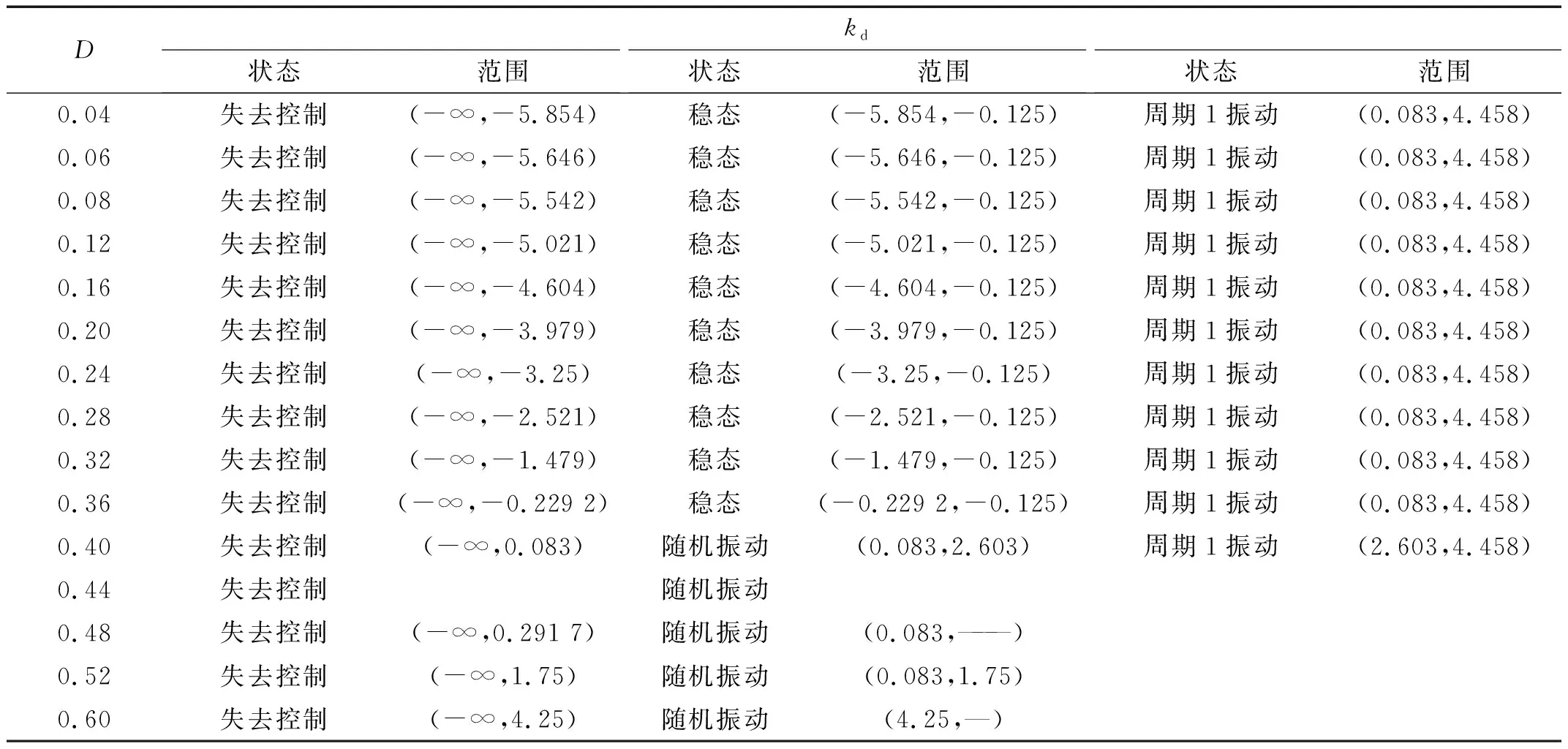
表1 不同随机强度下机组运行状态Tab.1 Operational states of the hydro-turbine generator with different levels of parameter D

3 结 论

本文考虑了随机波动扰速的影响，建立了新的水轮机调节系统随机动力学模型。在此基础上，利用随机逼近理论和非线性动力学理论，分析了随机激励对系统稳定性影响规律，可得以下结论：

(1)随机水轮机调节系统和原系统动态演化过程在宏观运行状态上比较相似，在随机转速波动影响下，随机系统稳定域、总能量等均发生变化。

(2)随着随机强度增加，关键点1及左侧不可调态整体向右平移，由于关键点1右侧不受随机激励影响，致使调速器参数kd的可调范围逐渐缩小。

(3)考虑到随机能源接入电网致使发电机转速随机波动性逐渐增大，推荐水电站调速器参数kd选值在保证机组稳定运行的可调范围内尽量大些。

参 考 文 献

[ 1 ] 沈祖仪. 水轮机调节[M].北京：水利水电出版社, 2008.

[ 2 ] 凌代俭. 水轮机调节系统分岔与混沌特性的研究[D]. 南京: 河海大学, 2007.

[ 3 ] 孔繁镍. 水轮机调节系统模型及其控制策略研究[D]. 南宁: 广西大学, 2013.

[ 4 ] 凌代俭，沈始祖. 考虑饱和非线性环节的水轮机调节系统的分叉分析[J]. 水力发电学报，2007,26(6):126-131.

LING Daijian, SHEN Shizu. Bifurcation analysis of hydro-turbine governing system with saturation nonlinearity[J]. Journal of Hydro Electric Engineering, 2007, 26(6):126-131.

[ 5 ] 陈帝伊，郑栋，马孝义，等. 混流式水轮机调节系统建模与非线性动力学分析[J]. 中国电机工程学报, 2012, 32(32): 116-123.

CHEN Diyi, ZHENG Dong, MA Xiaoyi, et al. Nonlinear dynamical analysis and mathematical model of hydro-turbine governing systems[J]. Proceedings of the CSEE, 2012, 32(32): 116-123.

[ 6 ] 郭文成，杨建东，王明疆. 基于HOPF分岔的变顶高尾水洞水电站水轮机调节系统稳定性研究[J]. 水利学报, 2016, 47(2): 189-199.

GUO Wencheng, YANG Jiandong, WANG Mingjiang. Stability analysis of hydro-turbine governing system of hydropower station with inclined ceiling tailrace based on hopf bifurcation[J]. Journal of Hydraulic Engineering, 2016, 47(2): 189-199.

[ 7 ] 许新勇, 职保平, 蒋莉, 等. 双扰动条件下水轮机竖向振动传导功率流分析[J]. 振动与冲击, 2016, 25(21): 63-68.

XU Xinyong, ZHI Baoping, JIANG Li, et al. Vertical vibration power flow of a water turbine under double-disturbance condition[J]. Journal of Vibration and Shock, 2016, 25(21): 63-68.

[ 8 ] 曾云，张立翔，钱晶，等. 电站局部多机条件下五阶发电机哈密顿模型[J]. 中国电机工程学报, 2014,34(3):415-422.

ZENG Yun, ZHANG Lixiang, QIAN Jing, et al. Fifth order generator Hamiltonian model under local multi-machine condition of a power station[J]. Proceedings of the CSEE, 2014, 34(3): 415-422.

[ 9 ] LIU Hongwei, LIN Yonggang, SHI Maoshun, et al. A novel hydraulic-mechanical hybrid transmission in tidal current turbines[J]. Renewable Energy, 2015，81: 31-42.

[10] LIU Xianlin, LIU Chu. Eigenanalysis of oscillatory instability of a hydropower plant including water conduit dynamics[J]. IEEE Transactions on Power Systems， 2007， 22(2): 675-683.

[11] 朱文龙, 周建中, 夏鑫, 等. 基于水电机组运行工况的水轮机压力脉动诊断策略[J]. 振动与冲击, 2015, 34(8): 26-40.

ZHU Wenlong, ZHOU Jianzhong, XIA Xin, et al. A novel diagnosis strategy for hydraulic turbine pressure pulsation based on operating state of a hydroelectric generating unit[J]. Journal of Vibration and Shock, 2015, 34(8): 26-40.

[12] 徐勤. 考虑风电不确定性的风电并网调度方法研究[D]. 镇江: 江苏大学, 2016.

[13] 王正伟, 刘艳艳, 赵潇然, 等. 水力机械转轮流固耦合特性分析与设计要素研究[J]. 水利水电技术, 2015, 46(6): 72-78.

WANG Zhengwei, LIU Yanyan, ZHAO Xiaoran, et al. Analysis on fluid-structure interaction characteristics of hydraulic machinery runner and study on tis design elements [J]. Water Resources and Hydropower Engineering, 2015, 46(6): 72-78.

[14] 国际水电协会. 2015年水电行业现状报告[R]. 北京：中国水利水电研究院, 2015.

[15] 宋志强, 马震岳. 考虑不平衡磁拉力的偏心转子非线性振动分析[J]. 振动与冲击, 2010, 29(8): 169-173.

SONG Zhiqiang, MA Zhenyue. Nonlinear vibration analysis of an eccentric rotor with unbalance magnetic pull [J]. Journal of Vibration and Shock, 2010, 29(8): 169-173.

[16] 王正伟, 杨校生, 肖业祥. 新型双向潮汐发电水轮机组性能优化设计[J]. 排灌机械工程学报, 2010, 28(5): 417-421.

WANG Zhengwei, YANG Xiaosheng, XIAO Yexiang. Hydraulic performance optimization of bidirectional tidal power turbine[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(5): 417-421.

[17] REN Mifeng, WU Di, ZHANG Jianhua, et al. Minimum entropy-based cascade control for governing hydroelectric turbines[J]. Entropy, 2014,16(6): 3136-1348.

[18] IEEE Working Group. Hydraulic turbinie and turbine control model for system dynamic studies[J]. IEEE Transaction on Power Systems, 1992, 7(1): 167-179.

[19] 肖若富, 陶然, 王维维, 等. 混流泵叶轮反问题设计与水力性能优化[J]. 农业机械学报, 2014, 45(9): 84-88.

XIAO Ruofu, TAO Ran, WANG Weiwei, et al. Inverse design and hydraulic optimization of mixed-flow pump impeller[J]. Transactions of The Chinese Society of Agricultural Machinery, 2014, 45(9): 84-88.

[20] 吴勤. 发动机转速波动的原因分析及解决方法[J]. 车用发动机, 2011(6): 35-36.

WU Qin. Reason analysis of engine rotate speed fluctuation and solvent[J]. Vehicle Engine, 2011(6): 35-36.

[21] 马少娟, 徐伟, 李伟, 等. 基于Chebyshev多项式随机逼近的随机van der Pol系统的被周期分岔分析[J]. 物理学报, 2005, 54(8): 3508-3515.

MA Shaojuan, XU Wei, LI Wei, et al. Period-doubling bifurcation analysis of stochastic van der Pol system via Chebyshev polynomial approximation[J]. Acta Physica Sinica, 2005, 54(8): 3508-3515.

[22] 徐伟.非线性随机动力学的若干数值方法及应用[M]. 北京: 科学出版社, 2013.