磁场中旋转运动圆板磁弹性超谐-组合共振

胡宇达， 秦晓北

(1. 燕山大学 建筑工程与力学学院，河北 秦皇岛 066004；2. 燕山大学 河北省重型装备与大型结构力学可靠性重点实验室，河北 秦皇岛 066004)

导电导磁结构件广泛应用于航空航天、超导发电机、电磁传感器、发动机等众多高新科技装置与设备中，处于电磁场中的导电弹性体因为受到电、磁、力等多种因素的作用，而表现出复杂的耦合动力学行为，或将直接影响系统运动的安全性与可靠性。近年来，许多学者展开了这一领域的研究。Moon 等[1]较早的对薄板的磁弹性屈曲问题进行了研究，提出了Moon-Pao模型，为后面研究的学者提供了很多的理论参考；郑晓静等[2-3]对磁场中铁磁梁式板、软铁磁壳的动力学特性进行了分析；Hasanyan等[4-5]研究了载流平板的磁弹性屈曲和后屈曲问题，并对处于倾斜磁场中的导电板的非线性振动问题进行了数学建模与研究；Takagi等[6]在考虑磁黏滞阻尼的影响下，采用了新的数值分析方法，对处于磁场环境中的薄板的动力学行为进行了研究；胡宇达等[7-10]研究了磁场中轴向运动导电薄板的非线性动力学行为以及旋转圆板的磁弹性主共振问题；Bayat等[11]对变厚度功能梯度环形旋转板的磁热机械响应进行了研究；Zenkour[12]研究了功能梯度环形夹层板的磁热弹性响应；高原文等[13]研究了横向磁场中铁磁梁式板的混沌运动问题；王省哲等[14]针对磁场中铁磁梁式板的磁弹性屈曲问题进行了研究；Bhandari等[15]研究了轴向非均匀磁场中旋转盘引起的铁磁流体的流动问题；Rad等[16]针对均布外激励作用下变厚度环形FGM板的磁热动力响应进行了分析。

在旋转结构动力学问题的研究中，Pei等[17]针对临界和超临界速度下的旋转柔性薄板进行了研究，分析了温度分布、热应力等对旋转盘动态稳定性及稳态振幅的影响。Sharma等[18]研究了变厚度及变密度弹性旋转环形薄板的有限差分解。Hussain等[19]研究了加速旋转盘在黏性流体中的数值解。Jabbari等[20]针对变厚度FGM旋转圆板进行研究，分析了厚度、角速度等参数对旋转盘力学性能的影响。

本文针对磁场环境中两频激励作用下的旋转运动导电圆板的谐波-组合共振问题进行研究，得到系统稳态解稳定的判定条件及幅频响应方程，绘制幅频特性曲线、动相平面轨迹图并分析系统不同物理参量对谐波-组合共振特性的影响。

1 旋转运动圆板磁弹性基本方程

1.1 应变能与动能

图1为旋转运动导电圆板在外加磁场B0作用下的示意图。圆板的板厚为h，半径为R，密度为ρ。

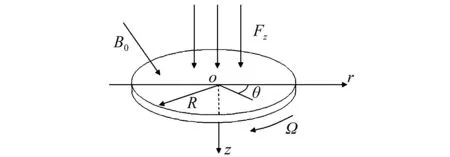
图1 旋转圆板示意图Fig.1 Rotating circular plate diagram

设旋转运动圆板内任意一点的位移为

ur1=ur+zu1

(1)

uθ1=uθ+zv1

(2)

uz=w

(3)

用位移表达的中面内力

(4)

(5)

(6)

则旋转圆板的中面应变势能表示为

(7)

用位移表示的弯矩，扭矩

(8)

(9)

(10)

则旋转圆板的弯曲应变势能表示为

(11)

板上任意一点的速度表达式

(12)

式中：i，j，k分别为坐标轴r，θ，z方向上的单位向量。

则旋转圆板的动能为

(13)

1.2 电磁力

旋转运动导电圆板电流密度表达式

J=σ0(E+V×B)

(14)

式中：σ0为电导率；E为电场强度矢量；B为磁感应强度矢量。

磁场环境中旋转运动圆板受到的洛伦兹力矢量表达式

f(fr,fθ,fz)=J×B0

(15)

(16)

(17)

(18)

则电磁力、电磁力矩在虚位移上所做的虚功为

(19)

假设圆板在横向位移w上产生了微小的变化量δw，则Fz在虚位移δw上所做的功为

(20)

1.3 振动方程

应用Hamilton原理建立旋转运动圆板的振动微分方程

(21)

将式(7)、式(11)、式(13)、式(19)和式(20)代入式(21)中，得到旋转运动导电圆板轴对称非线性磁弹性振动微分方程

(22)

2 周边夹支旋转板谐波-组合共振求解

2.1 振型函数与无量纲化方程

受组合动载荷Fz=F1cosω1t+F2cosω2t作用下做旋转运动的圆形薄板，设满足周边夹支边界条件的位移函数为

(23)

将式(23)代入式(22)，应用伽辽金法进行积分，推得旋转运动圆板无量纲化振动方程

(24)

2.2 共振问题的多尺度法求解

对于两频激励，考虑超谐波共振和组合共振同时发生的联合共振情况，系统的无量纲化频率为

(25)

式中：σ1，σ2为频率调谐参数。

(26)

采用多尺度法求解方程，取时间尺度T0=τ，T1=ετ，讨论一次近似解，可将式(26)的解表示为

q(τ,ε)=q0(T0,T1)+εq1(T0,T1)

(27)

将式(27)代入式(26)，令方程两端的ε0和ε1项的系数相等，可得到如下线性偏微分方程分别为

(28)

(29)

式(28)的通解为

q0=A(T1)eiT0+Λ1eiΩ1T0+Λ2eiΩ2T0+cc

(30)

将式(30)的通解代入式(29)，根据消除久期项的条件，得到关于A的关系式

(31)

(32)

(33)

分析式(32)和式(33)，当且仅当σ1T1-β和σ2T1-β都为常数时才能存在稳态运动，即β′=σ1=σ2=σ，同时，令γ=σT1-β，对于稳态运动a′=γ′=0，则由式(32)和式(33)可得到磁场环境下旋转运动圆板谐波-组合共振幅频响应方程

(34)

2.3 稳定性分析

研究系统稳态运动下解的稳定性问题，设

a=a0+a1,γ=γ0+γ1

(35)

式中：a0，γ0为系统稳态运动下的稳态解；a1，γ1为小的扰动量。

将稳态解a,γ代入式(32)和式(33)，并对小的扰动量a1，γ1进行Taylor展开，可得到关于a1和γ1的一阶线性近似式

(36)

(37)

根据Lyapunov稳定性近似理论，稳态运动下解的稳定性依赖于式(36)和式(37)右端系数矩阵的特征值。通过式(36)和式(37)的Jacobi矩阵并考虑到稳态运动下a′=γ′=0，可得到特征方程

(38)

再根据Hurwitz判据，可得系统稳态解稳定的充要条件

(39)

3 算例分析

针对磁场环境下受横向动载荷作用的铝制旋转圆形薄板进行数值分析，得到反映旋转运动圆板谐波-组合共振特性的图形。主要参数：密度ρ=2 670 kg/m3，泊松比μ=0.34，弹性模量E=71 GPa，电导率σ0=3.63×107(s/m)，圆板半径R=0.4 m。

图2为转速Ω=8 000 r/min时共振振幅a随频率调谐参数εσ的变化规律曲线图。由图2可知，在给定εσ范围内，共振幅频响应曲线向右偏移，呈现硬弹簧特性，随着εσ的改变，系统出现多值性和跳跃现象，呈现典型的非线性振动特性；随着磁感应强度的增加，共振曲线呈现明显的内缩趋势，共振区域变窄，振幅减小，可见磁场起到了电磁阻尼的作用；图2(b)、图2(c)和图2(d)中显示，随着板厚的减小，外激励力幅值F1，F2的增大，在给定的εσ范围内，系统共振区域变宽，激发多解区域的临界点呈滞后右移趋势。

图2 幅频a-εσ响应图Fig.2 Amplitude frequency response

图3为振幅a随磁感应强度B0z变化曲线图，取F1=500 N/m2，F2=1 000 N/m2，Ω=8 000 r/min和h=4.5 mm。从图3可知，在给定的B0z范围内，图中曲线呈现关于B0z=0左右对称形式，在给定调谐参数εσ范围内，曲线呈现从单值到多值并逐渐缩颈最终分离出上部的封闭曲线趋势；调谐参数的改变对曲线变化规律影响显著。图中由虚线分割的多值解区域中，区域1、区域3代表稳定解区域，区域2代表不稳定解区域。

图4为不同调谐参数下振幅a-力幅F1，F2的三维变化图，取B0z=0.5 T，h=4.5 mm及Ω=8 000 r/min。从图4可知，在给出的几种调谐参数下，激励力幅值F1=0时，无论F2取何值，共振振幅均为0，而当F≠0时，F2=0可能激发振动，激发的共振是超谐波共振。从F1等于某一值的截面看，共振振幅a随F2的变化曲线可以出现持续增加、先增加后减小或先减小后增加等多种复杂情况，调谐参数εσ的微小改变对曲线的影响显著。

图5为不同磁感应强度下振幅a-力幅F1，F2的三维变化图，取h=4.5 mm，εσ=0.001及Ω=8 000 r/min。从图5可知，磁感应强度取较小值时，振幅a随激励力幅值F1，F2变化曲线较复杂，振幅有先增加后减小或先减小后增加等多种形式，增大磁感应强度到某一值后，振幅呈单一增大趋势。

图6为h=4.5 mm时振幅a随外激励力幅值F1变化规律曲线图。从图6(a)可知，B0z=0.5 T时，小的F1就可以激发系统的多值解，当磁感应强度B0z增大到一定值后，系统的解退化为单值，共振振幅随之减小；从图6(b)可知，系统的解呈现从一个到三个再到一个的转变，随着转速的增大，系统的多值解区域变窄，共振曲线向左偏移；图6(c)为不同调谐参数下的a-εσ变化规律曲线，从图6(c)可知，εσ取值的大小决定了单值曲线到多值曲线的变化，随着εσ的增大，系统的多值解区域变宽，多值解区域共振振幅随之增加；图6(d)显示激励力幅值对共振曲线影响较大，当F2=0时，系统解呈现从单值到多值，后又变为单值的变化趋势，此时系统仅激发超谐波共振，增大F2，共振曲线继续向左偏移，解由多值逐渐退化为单值。

图7为Ω=8 000 r/min时振幅a随激励力幅值F2变化规律曲线图。图7(a)显示随着F1的增加，共振曲线向左偏移，呈现软弹簧特性，且随着磁感应强度B0z的增大，多值解区域减小，共振曲线呈明显内缩趋势；图7(b)、图7(c)显示随着板厚、调谐参数的增大，共振曲线向右偏移，激发多值解的临界点呈滞后右移趋势；图7(d)显示，随着F1的增大，共振曲线向左偏移，激发超谐-组合共振多值解所需要的激励力F2值减小，F1=0时，a-F2共振曲线不会被激发。

图3 振幅a-磁感应强度B0z响应图Fig.3 Amplitude-magnetic density response

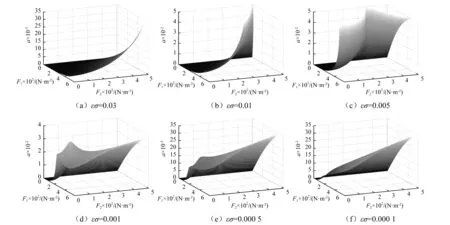
图4 振幅a-力幅F1，F2的三维变化图Fig.4 Three-dimensional variations of amplitude a-excitation amplitude F1， F2

图5 振幅a-力幅F1、F2的三维变化图Fig.5 Three-dimensional variations of amplitude a-excitation amplitude F1，F2

图6 振幅a-激励力幅值F1响应图Fig.6 Amplitude a-excitation amplitude F1

图8为改变初始条件得到的动相平面轨迹图，箭头指出了轨迹的运动方向，取参数F1=500 N/m2，F2=1 000 N/m2，h=4.5 mm，B0z=0.5 T，Ω=8 000 r/min。图中显示当调谐参数εσ取不同值时，稳态解的个数也不同。图8(a)只有一个稳定焦点S1，其共振振幅为aS=0.157，记为S1(aS=0.157)。图8(b)中显示有两个稳定焦点S1(aS=0.052)，S3(aS=0.393)和一个不稳定鞍点S2(aS=0.338)。可见，图8(b)中的稳态解与图8(c)中的结果是一致的，且图8(c)中的上支和下支曲线是稳定解，中部曲线是不稳定解，其解的不同取决于初始条件。

图9为取板厚h=4.5 mm，εσ=0.08时的动相平面轨迹图。图9(a)给出了不同磁感应强度下对应的两个稳定焦点，其中B0z=2 T对应点S1(aS=0.393)，B0z=0.5 T对应点S2(aS=0.381)；图9(b)给出了不同力幅F2下对应的两个稳定焦点，其中F2=800 N/m2和F2=1 000 N/m2分别对应点S1(aS=0.452)和S2(aS=0.393)。可见，参量的改变对系统非线性稳态解有显著影响。

图7 振幅a-激励力幅值F2响应图Fig.7 Amplitude a-excitation amplitude F2

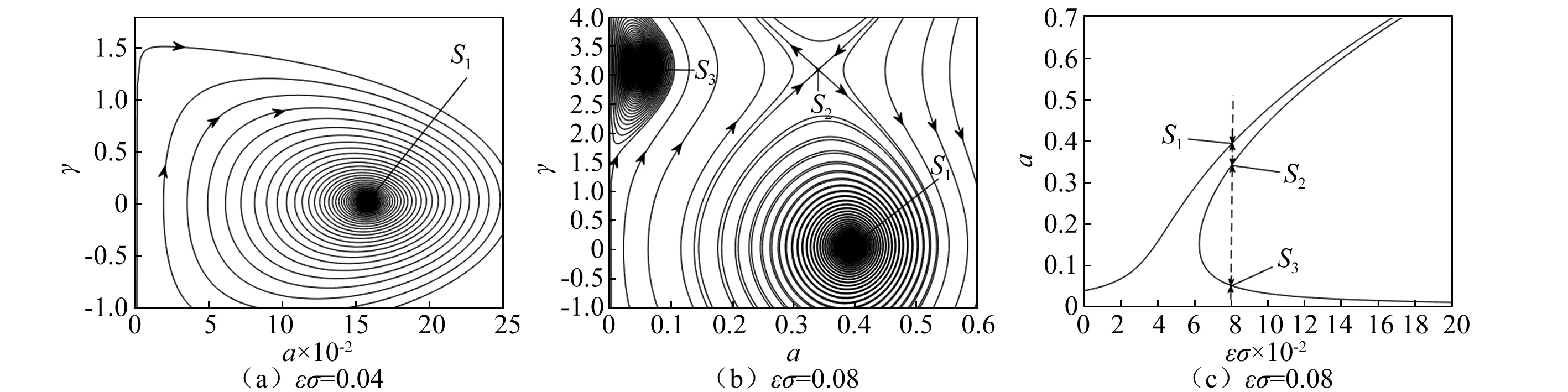
图8 动相平面轨迹Fig.8 Moving phase plane trajectory

图9 动相平面轨迹Fig.9 Moving phase plane trajectory

4 结 论

本文针对磁场环境中受两频激励作用旋转运动圆板的超谐-组合联合共振问题进行了研究，研究结果表明：

(1)在给定频率参数范围内，共振曲线向右偏移，呈硬弹簧特性，并出现多值性和跳跃现象，呈现典型的非线性振动特性。

(2)随着力幅的增加，共振曲线向左偏移，呈现软弹簧特性，且随着磁感应强度的增大，多值解区域减小，共振曲线呈明显内缩趋势。

(3)初始条件对非线性系统的稳态响应影响较大，幅频响应曲线上支和下支部分是稳定解，中间部分是不稳定解。由此可见，通过改变不同参量，可实现稳态解从多值到单值、稳定到不稳定的转变，从而达到控制系统共振现象的目的。

参 考 文 献

[ 1 ] MOON F C, PAO Y H. Magnetoelastic buckling of a thin plate [J]. ASME Journal of Applied Mechanics, 1968, 35(1): 53-68.

[ 2 ] 郑晓静，刘信恩. 铁磁导电梁式板在横向均匀磁场中的动力特性分析[J]. 固体力学学报， 2000，21(3)： 243-250.

ZHENG Xiaojing, LIU Xinen. Analysis on dynamic characteristics for ferromagnetic conducting plates in a transverse uniform magnetic field [J]. Acta Mechanica Solida Sinica, 2000, 21(3): 243-250.

[ 3 ] ZHENG X J, WANG X Z. A magnetoelastic theoretical model for soft ferromagnetic shell in magnetic field [J]. International Journal of Solids and Structures, 2003, 40(24): 6897-6912.

[ 4 ] HASANYAN D J, LIBRESCU L, AMBUR D R. Buckling and postbuckling of magnetoelastic flat plates carrying an electric current [J]. International Journal of Solids and Structures, 2006, 43(16): 4971-4996.

[ 5 ] HASANYAN D J, KHACHATURYAN G M, PILIPOSYAN G T. Mathematical modeling and investigation of nonlinear vibration of perfectly conductive plates in an inclined magnetic field [J]. Thin-Walled Structures, 2001, 39(1): 111-123.

[ 6 ] TAKAGI T, TANI J. New numerical analysis method of dynamic behavior of a thin plate under magnetic field considering magnetic viscous damping effect [J]. International Journal of Applied Electromagnetics in Materials, 1993, 4(1): 35-42.

[ 7 ] 胡宇达，胡朋. 轴向运动导电板磁弹性非线性动力学及分岔特性[J]. 计算力学学报，2014，31(2)：180-186.

HU Yuda, HU Peng. Magneto-elastic nonlinear dynamics and bifurcation of axially moving current-conducting plate [J]. Chinese Journal of Computational Mechanics, 2014, 31(2): 180-186.

[ 8 ] HU Y D, LI J. The magneto-elastic subharmonic resonance of current-conducting thin plate in magnetic field [J]. Journal of Sound and Vibration, 2009, 319(3/4/5): 1107-1120.

[ 9 ] HU Y D, WANG T. Nonlinear free vibration of a rotating circular plate under the static load in magnetic field [J]. Nonlinear Dynamics, 2016, 85(3): 1825-1835.

[10] 胡宇达，王彤. 磁场中导电旋转圆板的磁弹性非线性共振[J]. 振动与冲击，2016，35(12)：177-181.

HU Yuda, WANG Tong. Nonlinear resonance of a conductive rotating circular plate in magnetic field [J]. Journal of Vibration and Shock, 2016, 35(12): 177-181.

[11] BAYAT M, RAHIMI M, SALEEM M. One-dimensional analysis for magneto-thermo-mechanicl response in a functionally graded annular variable-thickness rotating disk [J]. Applied Mathematical Modelling, 2014, 38(19/20): 4625-4639.

[12] ZENKOUR A. On the magneto-thermo-elastic responses of fg annular sandwich disks [J]. International Journal of Engineering Science, 2014, 75(2): 54-66.

[13] 高原文, 周又和, 郑晓静. 横向磁场激励下铁磁梁式板的混沌运动分析[J]. 力学学报, 2002, 34(1): 101-108.

GAO Yuanwen, ZHOU Youhe, ZHENG Xiaojing. Analysis of chaotic motions of gemetrically nonliear ferromagnetic beam-plates exicited by transverse magnetic fields [J]. Acta Mechanica Sinica, 2002, 34(1): 101-108.

[14] 王省哲, 郑晓静. 铁磁梁式板磁弹性初始后屈曲及缺陷敏感性分析[J]. 力学学报, 2006, 38(1): 33-40.

WANG Xingzhe, ZHENG Xiaojing. Analysis on magnetoelastic initial post-buckling and sensitivity to imperfection for ferromagnetic beam-plates [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 33-40.

[15] BHANDARI A, KUMAR V. Ferrofluid flow due to a rotating disk in the presence of a non-uniform magnetic field [J]. International Journal of Applied Mechanics & Engineering, 2016, 21(1): 273-283.

[16] RAD A B, SHARIYAT M. Thermo-magneto-elasticity analysis of variable thickness annular fgm plates with asymmetric shear and normal loads and non-uniform elastic foundations [J]. Archives of Civil & Mechanical Engineering, 2016, 16(3): 448-466.

[17] PEI Y C, CHATWIN C, HE L, et al. A thermal boundary control method for a flexible thin disk rotating over critical and supercritical speeds [J]. Meccanica, 2017, 52(1/2): 383-401.

[18] SHARMA S, SANEHLATA Y. Finite difference solution of elastic-plastic thin rotating annular disk with exponentially variable thickness and exponentially variable density [J]. Journal of Materials, 2013 (5): 809205.

[19] HUSSAIN S, AHMAD F, SHAFIQUE M, et al. Numerical solution for accelerated rotating disk in a viscous fluid [J]. Applied Mathematics, 2013, 4(6): 899-902.

[20] JABBARI M, GHANNAD M, NEJAD M Z. Effect of thickness profile and fg function on rotating disks under thermal and mechanical loading [J]. Journal of Mechanics, 2016, 32(1): 35-46.