近场与远场长周期地震动对高层结构作用机理比较分析

王 博， 代慧娟， 吴 涛， 刘伯权

(1. 长安大学 建筑工程学院，西安 710061； 2. 西安科技大学 建筑与土木工程学院，西安 710054)

结构地震破坏模式主要分为首次超越破坏与累积损伤破坏两种类型，且最大响应与累积耗能的破坏界限相互影响[1-2]。文献[3]研究指出地震动最大瞬时输入能与结构最大位移响应具有较强的相关性，认为当最大瞬时输入能较小且总输入能较大时易发生累积损伤破坏；反之，易发生首次超越破坏。然而，该研究结论主要是基于普通地震动分析而来，其能否适用于长周期地震动有待进一步分析。此外，研究表明[4-6]，长周期地震动尚包括远场长周期地震动(亦称远场类谐和地震动)与近场长周期地震动(亦称近断层脉冲型地震动)两大类，而后者又包括近断层向前方向性地震动与近断层滑冲型地震动两种形式。同时，既有研究表明[7-10]，高层结构在长周期地震动作用下的地震响应明显大于普通地震动，且不同类型长周期地震动作用下的结构响应特征亦差异显著。然而，目前对不同类型长周期地震动及普通地震动作用下高层结构响应特征存在较大差异的内在机理尚未能揭示清楚。

鉴于此，本文以远场类谐和地震动、近断层向前方向性地震动及近断层滑冲型地震动三类长周期地震动为研究对象，首先在分析其最大瞬时输入能与SDOF体系最大位移响应相关性的基础上，探讨长周期地震动作用下的结构破坏模式；然后，以某高层RC(Reinforced Concrete)框架结构为例，分析长周期地震动对高层结构的作用机理。

1 长周期地震动作用下的结构破坏模式探讨

选择来自于1999年台湾7.6级集集地震的远场类谐和地震动、近断层向前方向性地震动及近断层滑冲型地震动各10条，如表1所示。采用MATLAB编制程序计算不同周期及延性系数下，每类长周期地震动最大瞬时输入能与SDOF(Single Degree of Freedom)体系最大位移响应间的相关系数。其中，瞬时输入能IE为连续两速度零点间的能量输入，如式(1)所示。相关系数计算式如式(2)所示[11]。SDOF体系的自振周期分别取0.1 s，0.2 s，0.5 s，1.0 s，1.5 s，2.0 s，4.0 s，6.0 s，8.0 s，10.0 s，采用双线性恢复力模型，屈服后刚度折减系数取0.05，延性系数分别取2，3，5，阻尼比取5%。

(1)

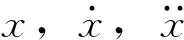
(2)

式中：X，Y分别为长周期地震动最大瞬时输入能与SDOF体系最大位移响应。

表1 长周期地震动的基本信息

图1为三类长周期地震动最大瞬时输入能与最大位移响应的相关系数计算结果。

由图1可以看出，自振周期对长周期地震动最大瞬时输入能与最大位移响应的相关性程度影响显著。当自振周期大于1.0 s时，三类长周期地震动的最大瞬时输入能与SDOF体系最大位移响应均具有较强的相关性，最大瞬时输入能越大，最大位移响应就越大。鉴于此，参考胡冗冗等的研究分析认为，可通过最大瞬时输入能与总输入能的相对大小来分析长周期地震动作用下中长周期结构的破坏模式。

为量化对比分析，定义瞬时输入能比为最大瞬时输入能与总输入能的比值，如式(3)所示。瞬时输入能比越大，结构越易发生首次超越破坏；反之，易发生累积损伤破坏。

图1 长周期地震动最大瞬时输入能与SDOF体系最大位移响应的相关性Fig.1 The correlation between the maximum instantaneous input energy and the maximum displacement response of SDOF system for three types of long-period ground motions

(3)

表2为表1中30条长周期地震动的瞬时输入能比计算结果。由表2可知，远场类谐和地震动的瞬时输入能比普遍小于近断层向前方向性地震动与近断层滑冲型地震动，其中，近断层滑冲型地震动对应的瞬时输入能比最大。这说明，近断层滑冲型地震动与近断层向前方向性地震动作用下，结构易发生首次超越破坏，而远场类谐和地震动作用下，结构易发生累积损伤破坏。

表2 长周期地震动瞬时输入能比的平均值计算结果

2 基于HHT的长周期地震动IMF分量对结构弹塑性地震响应的影响分析

2.1 HHT基本理论

Hilbert-Huang变换(Hilbert-Huang Transform，HHT)是一种非平稳信号处理方法[12-14]，主要包括经验模态分解(Empirical Mode Decomposition, EMD)与Hilbert谱分析两部分。首先通过EMD可将信号分解为若干本征模态函数(Intrinsic mode function, IMF)，图2为EL Centro 地震动通过经验模态分解得到的9个IMF分量与1个残量，可以看出不同分量所处的频段不同；然后，对每个IMF分量进行Hilbert变换可得到其Hilbert谱，最后汇总各IMF的Hilbert谱即可得到原始信号的Hilbert谱，如式(4)所示。

(4)

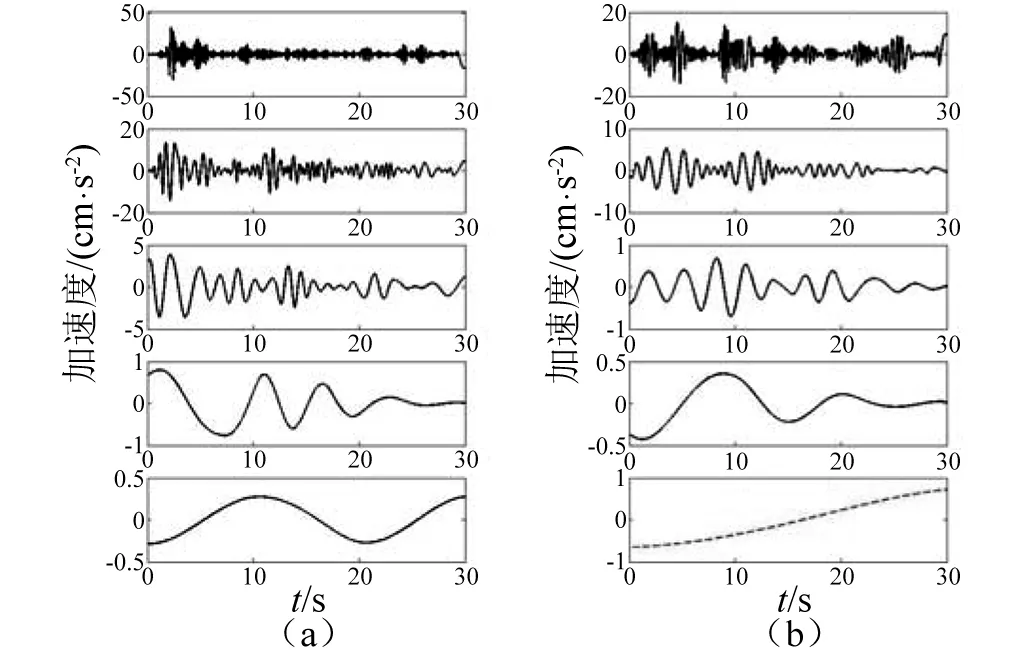
图2 EL centro地震动IMF分量Fig.2 IMF of EL centro ground motion

将H(ω,t)对时间积分可得Hilbert边际谱，可反映信号幅值在频域内的分布情况，如式(5)所示

(5)

将H(ω,t)的平方对时间积分可得Hilbert能量谱，可反映频率信号在持时内累积的能量，如式(6)所示

(6)

将H(ω,t)的平方对频率积分可得到瞬时能量，可反映信号能量随时间的变化情况，如式(7)所示

(7)

2.2 分析步骤与方法

(1) 建立有限元分析模型。采用ABAQUS软件建立某12层RC框架结构有限元模型，如图3所示。该结构依据我国现行规范[15-16]设计，抗震设防烈度为7度，Ⅲ类场地。分别采用梁单元B31与壳单元S4R模拟梁柱构件及楼板。梁柱混凝土材料本构选用PQ-Fiber纤维模型中的UCONCRETE02；钢筋本构选用PQ-Fiber模型中的USTEEL02；楼屋面板采用ABAQUS自带的混凝土塑性损伤本构模型[17]。动力特性分析表明，结构基本自振周期为2.22 s。

(2) 对长周期地震动进行EMD。选择3条典型的长周期地震动ILA056-NS、TCU094-NS、TCU052-NS，将峰值加速度均调整至220 gal。基于EMD获得每条地震动的各IMF分量。各IMF分量的峰值及所在频段不同，考虑到长周期地震动最后两个或三个IMF分量一般峰值较小，且所处频段对应的周期远大于结构的基本自振周期，为简化计算，不予考虑。

(3) 依次去掉每一个IMF分量，将其余IMF分量叠加重构而成新的地震动。对于ILA056-NS，依次去掉第1～第6个IMF分量，可得到6条新地震动，依次命名为H1,H2,H3,H4,H5,H6；对于TCU094-NS，依次去掉1～6个IMF分量，可得到6条新地震动，依次命名为D1,D2,D3,D4,D5,D6；对于TCU052-NS，依次去掉第1～第5个IMF分量，可得到5条新地震动，依次命名为F1,F2,F3,F4,F5。

(4) 分别计算3条原始长周期地震动及重构而成的17条新地震动作用下框架结构的弹塑性地震响应，基于计算结果对比分析不同IMF分量对结构地震响应的影响。为量化分析各IMF分量的影响程度，定义偏差度为原始地震动与重构地震动所对应响应值之差占原始地震动所对应响应值的百分比。偏差度越大，说明所去掉的该IMF分量对结构响应的影响程度越大。

2.3 计算结果分析

图4为各重构地震动及原始长周期地震动作用下结构的楼层位移。表3为重构地震动作用下结构顶点最大位移及偏差度的计算结果，其中，对偏差度较大的数字加下划线以突出显示。

图4 长周期地震动原始与重构地震动作用下结构楼层位移响应对比Fig.4 Comparison of floor displacement responses between the original and reconstructed long-period ground motions

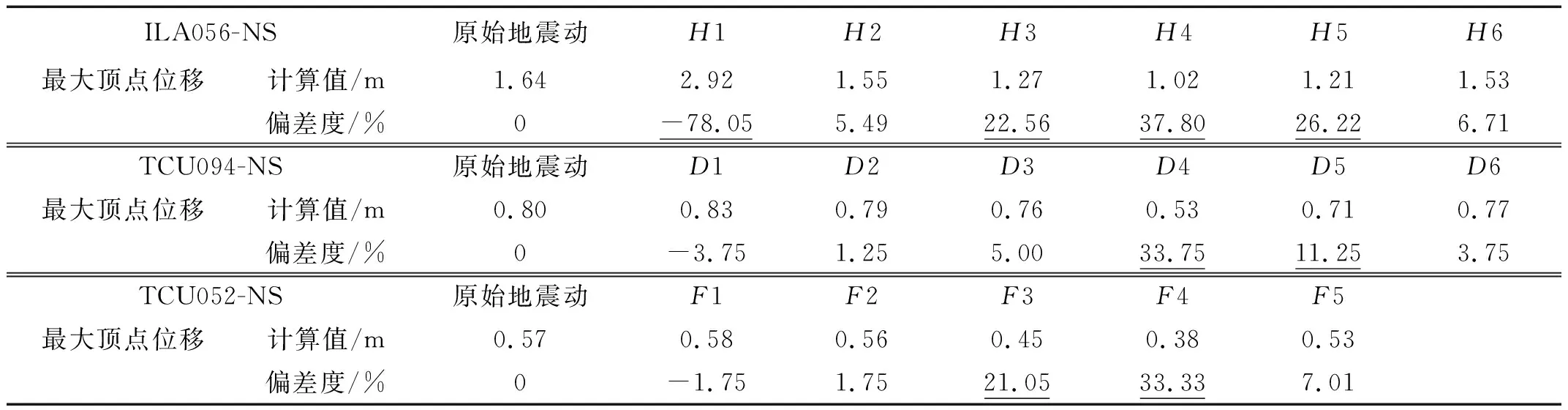
ILA056-NS原始地震动H1H2H3H4H5H6最大顶点位移计算值/m1.642.921.551.271.021.211.53偏差度/%0-78.055.4922.5637.8026.226.71TCU094-NS原始地震动D1D2D3D4D5D6最大顶点位移计算值/m0.800.830.790.760.530.710.77偏差度/%0-3.751.255.0033.7511.253.75TCU052-NS原始地震动F1F2F3F4F5最大顶点位移计算值/m0.570.580.560.450.380.53偏差度/%0-1.751.7521.0533.337.01

由图4及表3可知：对于ILA056-NS地震动，去掉第3、第4、第5个IMF分量时，最大顶点位移减小幅度较大，而去掉第1个IMF分量时，最大顶点位移则出现大幅度的增大；对于TCU094-NS地震动，去掉第4、第5个IMF分量时，最大顶点位移减小幅度较大；对于TCU052-NS，去掉第3、第4个IMF分量时，最大顶点位移减小幅度较大；此外，对于两种近场长周期地震动TCU094-NS与TCU052-NS，在去掉第1个IMF分量后，最大顶点位移仅略微增大，增幅远小于远场类谐和地震动ILA056-NS。

结合各IMF分量所在频段分析认为，只有当去掉与结构基本自振周期较接近且峰值较大的IMF分量时，结构响应才会有较大幅度的减小。此外，初步分析认为第1个IMF分量(高频分量)对结构响应具有干扰作用，去掉该分量后会引起结构响应的增大，且远场类谐和地震动高频分量的干扰作用不容忽视。

3 长周期地震动有效峰值的定义与分析

由上述分析可知，长周期地震动部分IMF分量对结构响应的影响较小，可忽略不计。鉴于此，为便于分析，将对结构响应影响较大的IMF分量叠加重构而成新的地震动，称为有效长周期地震动。图5为对应于本文分析用框架结构的有效长周期地震动及原始长周期地震动的加速度时程曲线。通过试算分析，对于远场类谐和地震动ILA056-NS，其有效长周期地震动由第3～第6个IMF分量与第1个高频IMF分量叠加重构而成，而对于近断层向前方向性地震动TCU094-NS与近断层滑冲型地震动TCU052-NS，其有效地震动均由第3～第5个IMF分量叠加重构而成。需要说明的是，有效长周期地震动的量化控制与结构特性、地震动特性及地震动各IMF分量对结构响应的相对影响程度均相关，还有待于进一步的深入研究。

图6为有效长周期地震动与原始长周期地震动作用下结构楼层位移的对比情况。需要说明的是，对于远场类谐和地震动ILA056-NS，为进一步分析验证高频IMF分量的干扰作用，分别计算第1个IMF分量(纯高频地震动)、由第3～第6个IMF分量叠加重构而成的地震动(不含高频地震动)，以及由第1个与第3～第6个IMF分量叠加重构而成的地震动(含高频地震动，即有效长周期地震动)作用下的结构响应。可以看出，纯高频地震动作用下的结构响应较小，但去掉第一个高频IMF分量后，结构响应却显著大于原始地震动，而在叠加该高频IMF分量重构而成的有效地震动作用下，结构响应与原始地震动比较接近。采用其它远场类谐和地震动进行计算亦得到同样的结论。这说明，在构建远场类谐和地震动的有效地震动时，高频IMF分量的影响不容忽视。同时，由图6(b)、图6(c)可知，对于近断层向前方向性地震动与近断层滑冲型地震动，其有效地震动与原始地震动作用下的结构响应均比较接近，这说明本文提出的有效长周期地震动的构建方法是合理的。关于高频分量对结构响应的影响机理，作者初步分析认为，其与地震动的特性及结构特性均相关，有待于后续针对该问题进行深入研究。

为进一步分析，定义有效长周期地震动的加速度峰值为有效峰值，定义有效峰值占原始地震动峰值加速度的百分比为有效峰值率。计算表1中30条长周期地震动及10条普通地震动对应于本文分析用框架结构的有效峰值与有效峰值率，如表4所示。对比结果表明，三类长周期地震动的有效峰值均大于普通地震动，分析认为这是导致长周期地震动作用下高层结构的地震响应普遍大于普通地震动的内在原因。同时，可以看出，普通地震动的有效峰值率均在30%以下，远小于三类长周期地震动(普遍在80%以上)，分析认为这是由于普通地震动的IMF分量主要集中于高频段，对高层框架结构影响较大的低频IMF分量较少且峰值较小引起的。

图5 有效长周期地震动与原始长周期地震动加速度时程比较Fig.5 Comparison of acceleration time-history curves between the valid and original long-period ground motions

图6 有效长周期地震动与原始长周期地震动作用下结构楼层位移响应对比Fig.6 Comparison of floor displacement responses under the valid and original long-period ground motions

4 长周期地震动能量梯度的定义与分析

基于Hilbert-Huang变换(HHT)，通过对比分析不同类型长周期地震动的瞬时能量曲线及累积能量曲线，尝试从时域角度进一步分析长周期地震动对高层结构的作用机理。图7和图8分别为代表性长周期地震动ILA056-NS、TCU094-NS和TCU052-NS的瞬时能量曲线与累积能量曲线。

由图7和图8可知：

(1) 远场类谐和地震动ILA056-NS在0～20 s与28.20～59.81 s内均包含较大能量，且两段内的瞬时能量最大值较为接近，分别为226.8 cm2/s3与207.8 cm2/s3，但所对应的累积能量相差较大，前、后两者分别为1 577 cm2/s2与2 532 cm2/s2，后者约为前者的1.61倍，约占地震动总能量的61.62%。此外，两部分的持时均较长，分别为20 s与30 s，能量释放较为平缓。

表4 有效峰值及有效峰值率计算结果

(2) 近断层向前方向性地震动TCU094-NS存在多个较大的瞬时能量，最大值为386.10 cm2/s3，远大于远场类谐和地震动，但其累积能量仅为远场类谐和地震动ILA056-NS的61.22%，且持时较短，仅为远场类谐和地震动的一半，能量主要集中分布于12.36～27.50 s区段内，累积能量为1 749.7 cm2/s2，约占总能量的69.63%，能量释放比较集中。

(3) 近断层滑冲型地震动TCU052-NS的最大瞬时能量为456 cm2/s3，大于近断层向前方向性地震动，且约为远场类谐和地震动的2倍，而在6.96 s的脉冲段内所包含的能量达到737.8 cm2/s2，约占总能量的58.74%，能量释放急剧。

统计分析表1中30条长周期地震动的瞬时能量曲线，可以看出不同类型长周期地震动在时域内的能量分布特征存在较大差异，并可通过速度脉冲持时及最大瞬时能量这两个参数来体现。其中，远场类谐和地震动与近断层滑冲型地震动在脉冲持时内的瞬时能量曲线可近似为三角形脉冲，如图9所示。由图9中的虚线与细实线对比可知，当最大瞬时能量相同时，脉冲持时越长，总能量就越大；由图9中的细实线与粗实线对比可知，当脉冲持时相同时，最大瞬时能量越大，总能量就越大。对于近断层向前方向性地震动，其含有多个脉冲段，而每个局部瞬时能量脉冲段亦可简化为三角形脉冲，在整个脉冲持时内的瞬时能量曲线可近似为多个交错三角形。

为定量对比分析不同类型长周期地震动的能量分布情况，提出能量梯度GE的概念，如式(8)所示。能量梯度主要用来反映地震动瞬时能量的变化率，能够体现能量释放的剧烈程度。能量梯度越大，说明地震动的能量释放越集中，从而使结构在较短时间内塑性变形急剧增加，易发生首次超越破坏；能量梯度越小，说明地震动能量释放越平缓，从而使结构塑性变形充分发展，易发生累积损伤破坏。其计算原理是将每个有效局部瞬时能量脉冲段均简化等效为三角形脉冲，首先求出对于每个有效局部瞬时能量脉冲段内的局部能量梯度；然后再依据各局部瞬时能量脉冲段所包含的能量对每个局部能量梯度进行加权。

图7 瞬时能量曲线Fig.7 Transient energy curves

图8 累积能量曲线Fig.8 Accumulative energy curves

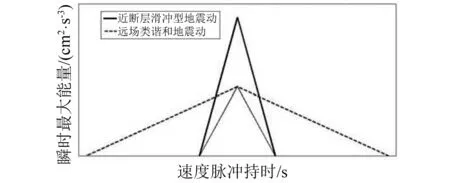
图9 瞬时能量曲线简化示意图Fig.9 Simplified sketches of instantaneous energy curves

(8)

式中：n为有效局部能量脉冲段的个数，规定当局部最大瞬时能量不小于速度脉冲段内最大瞬时能量的50%时为有效局部能量脉冲。该规定可从某种程度上考虑脉冲段总能量的影响，因为对于持时与最大瞬时能量均较小的脉冲段，其能量梯度亦可能较大，然而却因其所包含的总能量较小而不会对结构产生较大破坏作用。GEi为第i个有效局部能量脉冲段的能量梯度； ΔEi为第i个有效局部能量脉冲段内上升段最大瞬时能量与最小瞬时能量之差； ΔTi为第i个有效局部能量脉冲段内最小瞬时能量增至最大瞬时能量所需的时间。

当仅含有1个脉冲段时，n取1，式(8)便退化为式(9)，可直接用于远场类谐和地震动及近断层滑冲型地震动能量梯度的计算。

(9)

按照上述方法计算表1中30条长周期地震动的能量梯度分布情况，如图10所示。

由图10可知，远场类谐和地震动的能量梯度显著小于近断层向前方向性地震动与近断层滑冲型地震动，且近断层滑冲型地震动的能量梯度最大。这说明，远场类谐和地震动的能量释放最为平缓，考虑其类谐和振动特征，可将其对高层结构的作用称为脉冲循

图10 三类长周期地震动能量梯度的对比Fig.10 Comparison of energy gradients for three types of long-period ground motions

环作用，在该类地震动作用下结构易发生累积损伤破坏；近断层向前方向性地震动与近断层滑冲型地震动的能量释放比较集中，考虑其大速度脉冲特征，可将其对高层结构的作用称为脉冲冲击作用，且近断层滑冲型地震动的脉冲冲击作用更强，在此两类地震动作用下结构易发生首次超越破坏。分析认为，这是导致不同类型长周期地震动作用下高层结构响应特征存在较大差异的内在原因。同时，可以看出，三类长周期地震动作用下结构破坏模式的分析结论同“1”节基于瞬时输入能比的分析结论一致。

5 结 论

(1) 在中长周期范围内，长周期地震动最大瞬时输入能与弹塑性SDOF体系最大位移响应存在较强的相关性，最大瞬时输入能越大，最大位移响应就越大。提出以瞬时输入能比作为分析结构地震破坏模式的指标，结果表明，远场类谐和地震动作用下，高层结构易发生累积损伤破坏，而近断层向前方向性地震动与近断层滑冲型地震动作用下，则易发生首次超越破坏。

(2) 提出有效长周期地震动的概念，定义了有效峰值与有效峰值率，分析表明，长周期地震动的有效峰值及有效峰值率普遍大于普通地震动，进而揭示了导致长周期地震动作用下高层结构的地震响应大于普通地震动的内在原因。

(3) 提出长周期地震动能量梯度的概念，分析表明，三类长周期地震动的能量释放特征差异显著，其中，远场类谐和地震动的能量释放最为平缓，揭示了该类地震动对高层结构的脉冲循环作用机理，近断层向前方向性地震动与近断层滑冲型地震动的能量释放比较集中，揭示了此两类地震动对高层结构的脉冲冲击作用机理，且近断层滑冲型地震动的冲击作用最强，分析认为这是导致三类长周期地震动作用下结构地震响应存在较大差异的内在原因。

(4) 本文虽初步从频域与时域的角度揭示了长周期地震动对高层结构的作用机理，但诸如有效长周期地震动的参数量化控制、长周期地震动高频分量对结构响应的干扰机理等问题还有待于进一步深入研究。

参 考 文 献

[ 1 ] 于琦，孟少平，吴京. 基于变形与能量双重准则的钢筋混凝土结构地震损伤评估[J]. 土木工程学报，2011，44(5): 16-23.

YU Qi, MENG Shaoping, WU Jing. Deformation and energy-based seismic damage evaluation of reinforced concrete structures[J]. China Civil Engineering Journal, 2011，44(5): 16-23.

[ 2 ] 黄庆丰，王大富. 钢筋混凝土结构的地震损伤分析及能量参数模型[J]. 地震工程与工程震动，2010，30(5): 93-99.

HUANG Qingfeng, WANG Dafu. Analysis of seismic damage to reinforced concrete structures and energy parameter model[J]. Earthquake Engineering and Engineering Vibration, 2010, 30(5): 93-99.

[ 3 ] 胡冗冗，王亚勇. 地震动瞬时输入能量与结构最大位移反应关系研究[J]. 建筑结构学报，2000，21(1): 71-76.

HU Rongrong, WANG Yayong. A study on relation instantanesous energy of earthquake strong motion and maximum displacement response of structures[J]. Journal of Building Structures, 2000，21(1): 71-76.

[ 4 ] 杜东升，王曙光，刘伟庆，等. 长周期地震动影响因素及频谱参数研究[J]. 建筑结构学报，2014，35(增刊1): 1-8.

DU Dongsheng, WANG Shuguang, LIU Weiqing, et al. Study on affecting factors and spectral parameters of long period ground motions[J]. Journal of Building Structures, 2014，35(Sup 1): 1-8.

[ 5 ] 李雪红，王文科，吴迪，等. 长周期地震动的特性分析及界定方法研究[J]. 振动工程学报，2014，27(5): 685-692.

LI Xuehong, WANG Wenke, WU Di, et al. The bounded method and characteristics analysis for long-period ground motions[J]. Journal of Vibration Engineering, 2014,27(5): 685-692.

[ 6 ] KALKAN E, KUNNATH S K. Effects of fling step and forward directivity on seismic response of buildings[J]. Earthquake Spectra, 2006, 22(2): 367-390.

[ 7 ] 陈清军，袁伟泽，曹丽雅. 长周期地震波作用下高层建筑结构的弹塑性动力响应分析[J]. 力学季刊，2011，32(3): 403-410.

CHEN Qingjun, YUAN Weize, CAO Liya. Elasto-plastic dynamic response analysis of high-rise structures under long period ground motion[J]. Chinese Quarterly Mechanics，2011, 32(3): 403-410.

[ 8 ] 杉本訓祥，塩原，勝俣英雄，等. 縮小 20 層 RC 造建物試験体の長周期地震動による震動実験(その1～その11)[C]//日本建築学会会议. 北海道：日本建築学会大会学術講演梗概集, 2013.

[ 9 ] 马华，曹飞，唐贞云，等. 高层框架结构E-defense振动台试验弹塑性时程对比分析[J]. 地震工程与工程振动，2015，35(1): 143-149.

MA Hua, CAO Fei, TANG Zhenyun, et al. Comparative analysis of E-defense shaking table test and nonlinear time history simulation for high-rise frame structure[J]. Earthquake Engineering and Engineering Vibration, 2015, 35(1): 143-149.

[10] 杨迪雄，潘建伟，李刚. 近断层脉冲型地震动作用下建筑结构的层间变形分布特征和机理分析[J]. 建筑结构学报，2009，30(4): 108-118.

YANG Dixiong, PAN Jianwei, LI Gang. Deformational distribution feature and mechanism analysis of building structures subjected to near-fault pulse-type ground motions[J]. Journal of Building Structures, 2009, 30(4): 108-118.

[11] YANG D X, PAN J W, LI G. Non-structure-specific intensity measure parameters and characteristic period of near-fault ground motions[J]Earthquake Engineering and Structural Dynamics, 2009, 38(11): 1257-1280.

[12] 王博，白国良，代慧娟. 典型地震动作用下长周期单自由度体系地震反应分析[J]. 振动与冲击，2013，32(15): 190-196.

WANG Bo, BAI Guoliang, DAI Huijuan. Seismic response analysis of long-period SDOF system under typical ground motions[J]. Journal of Vibration and Shock, 2013,32(15): 190-196.

[13] 吴琛，周瑞忠. Hilbert-Huang变换在提取地震信号动力特性中的应用[J]. 地震工程与工程振动，2006, 26(5): 41-46.

WU Chen, ZHOU Ruizhong. Application of Hilbert-Huang transform in extracting dynamic properties of seismic signals[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 41-46.

[14] 张郁山. 希尔伯特-黄变换(HHT)与地震动时程的希尔伯特谱—方法与应用研究[D]. 北京：中国地震局地球物理研究所，2003.

[15] 建筑抗震设计规范：GB 50011—2010 [S]. 北京：中国建筑工业出版社，2016.

[16] 抗震设计规程：DGJ 08-9—2013 [S]. 北京：中国建筑工业出版社，2013.

[17] 陆新征，叶列平，缪志伟，等. 建筑抗震弹塑性分析—原理、模型与在ABAQUS, MSC.MARC和SAP2000上的实践[M]. 北京：中国建筑工业出版社，2009.