乘性双态噪声和周期调制简谐噪声激励下的线性过阻尼谐振子的随机共振
2018-06-28钟苏川
张 路, 钟苏川
(1. 四川大学 数学学院,成都 610065; 2. 四川大学 空天科学与工程学院, 成都 610065)
随着对随机振动理论研究的深入,学者们逐渐认识到噪声对随机动力系统并不总起破坏作用,而是会产生多种积极的、建设性的重要效应[1]。因此,针对随机动力系统中噪声所诱导的各种非线性效应,研究这些效应产生的条件、机制和应用,已经成为近年来非线性科学发展的一个重要的任务。对许多受随机噪声作用的动力系统,系统响应的某些函数(如输出信噪比、矩、自相关函数、功率谱或信噪比等)随噪声的某些特征参数(如噪声的强度、相关率等)呈现非单调性,这类现象被称为随机共振(Stochastic Resonance, SR)。随机共振的概念最早是由Benzi等[2]在20世纪80年代为解释第四季冰川问题而提出的。随后,人们针对各种系统和噪声协同作用产生的随机共振现象进行了深入的研究[3-8],发现随机共振是随机动力系统中非常普遍的一类现象,这也因此引起了人们的普遍关注和浓厚兴趣,并将其广泛应用于激光物理、生物物理、化学物理及工程信号处理等诸多领域。对各类随机共振现象及其控制的研究不仅对物理学的研究起着重要的作用,也对工程实际应用有着特殊的价值。
对随机共振现象的早期研究主要集中在白噪声驱动的非线性系统,研究认为非线性系统是发生随机共振的一个必要条件。随后,Fulinski[9]用数值方法研究了非Markov噪声作用的一个线性随机流模型,发现系统的输出信噪比对噪声强度也存在非单调的依赖关系。Berdichevsky[10]讨论了受乘性色噪声驱动的线性系统,发现系统稳态响应的幅值增益关于噪声强度和相关时间非单调变化。在此之后,很多由乘性色噪声作用的线性系统中都发现了随机共振现象[11-19]。我们之前的工作,发现由乘性二次色噪声和周期调制噪声联合驱动的线性过阻尼系统,系统稳态响应振幅和方差均存在随机共振现象[20]。
事实上,自然界中不存在真正的白噪声,所有噪声都有长短不一的相关时间(即为色噪声),只有噪声相关时间远小于确定系统的驰豫时间时,噪声之间的关联才可以近似为零从而当作白噪声处理[21]。然而,还有很多色噪声广泛存在于各类实际系统,例如,双态噪声(Dichotomous Noise)又称随机电报噪声,是两态泊松过程的实现[22],即普遍存在于金属、超导薄膜、纳米器件、双极型晶体管等器件和材料中,常以对电阻、电导、电压或电流的影响表现出来。同时,双态噪声是两状态泊松过程的实现,当噪声相关率趋于无穷时,它将退化为高斯白噪声。而简谐噪声(Harmonic Noise)作为一种常用的准单色噪声,是由白噪声驱动一个阻尼谐振子而生成的[23],此类噪声不仅具有噪声强度,关联时间还具有频率特征,可由噪声强度,频率参数以及阻尼参数共同控制噪声的形式[24-25],但是现有文献对简谐噪声诱导的随机动力学特性的报道还非常少,因此对其激励的随机振动系统进行讨论研究有着重要的理论和实际意义。另一方面,通常的加性噪声与乘性噪声由于起源的内在机制不同, 因此在同一模型中总被建模成相互独立的噪声,但是在某些特殊情况下,这两种噪声可能有共同的物理起源,或者在某种条件下, 这二种噪声相互耦合, 从而表现出相关性[26]。因此,研究噪声的相关时间以及相关噪声的相关性对随机系统各种物理性质的影响,是一个完整的随机理论不可缺少的方面,而且我们也将在本文的研究结果中发现,相互关联的色噪声会使随机系统表现成简单白噪声情况下完全不同的性质。因此,对这类噪声所产生的非线性效应,也有必要进行深入的研究。此外,将双态噪声以乘性方式,简谐噪声以周期调制的方式引入线性系统可得到一个精确可解的模型, 而具有精确可解的模型更容易应用到各门具体学科的研究中。
本文针对由乘性双态噪声和周期调制简谐噪声联合驱动的线性过阻尼系统,推导了系统稳态响应稳定的充分条件及其振幅的解析表达式,并通过其解析表达式理论分析了系统稳态响应振幅关于噪声强度、噪声相关率、非对称性、关联率等参数存在随机共振现象所需满足的条件,发现了此类系统系统稳态响应振幅关于各种噪声参数具有随机共振现象。
1 系统模型
本文考虑具有乘性色噪声和周期调制色噪声外激励的线性过阻尼系统,它的随机微分方程

(1)
式中:ξ(t)为具有零均值和非零相关函数的色噪声, 满足〈ξ(t)〉=0, 〈ξ(t)ξ(s)〉=Dξλξexp(-λξ|t-s|);Dξ为色噪声强度;λξ为色噪声的相关率。假设ξ(t)为非对称的双态随机过程, 并且ξ(t)在{A1,-B1}中取值,A1,B1均为正数,ξ(t)的非对称性用Δξ=A1-B1表示。y(t)为由白噪声驱动一个阻尼谐振子而生成的简谐噪声,满足如下方程
(2)
式中:η(t)为一个具有零均值和非零相关函数的白噪声, 满足〈η(t)〉=0, 〈η(t)η(s)〉=2Dηδ(t-s);Dη为白噪声强度。 阻尼参数Γ>0主要影响简谐噪声的频域带宽; 频率参数ΩE>0则主要影响噪声的中心频率位置。由于式(1)中的y(t)为线性二阶式(2)的系统响应, 因此,求解式(2)可以得到简谐噪声y(t)的解析表达式为
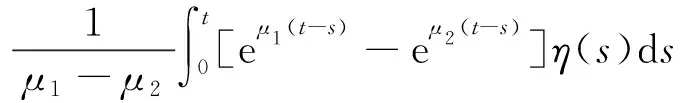
(3)

(4)
经过推导可得简谐噪声的稳定相关函数为
(5)
它的相关时间则定义为
(6)
当Γ→∞,ΩE→∞,τy为常数时,简谐噪声可退化成O-U噪声,进一步,若τy→0,简谐噪声退化为白噪声。
同时,假设ξ(t)和η(t)为两个相关噪声,满足
(7)
式中:κ>0为双态噪声ξ(t)和白噪声η(t)的关联系数;λξη>0为关联率。
2 系统响应的一阶稳态矩及响应振幅
对式(1)两边取均值得到

(8)
对式(3)两边取均值可得

(9)
将式(9)代入式(8)有

(10)
式(1)两边同时乘以ξ(t)并取均值得到
(11)
另外,ξ(t)为双态噪声, 由Shapiro-Loginov公式[27]得到

(12)
又由ξ(t)是一个两态随机过程,满足
〈ξ2x〉=Dξλξ〈x〉+Δξ〈ξx〉
(13)
将式(12),式(13)代入式(11)化简后可得

(14)
同时,在y(t)的解析表达式式(3)两边同时乘以ξ(t)并取均值, 同时利用〈ξ(t)〉=0得到
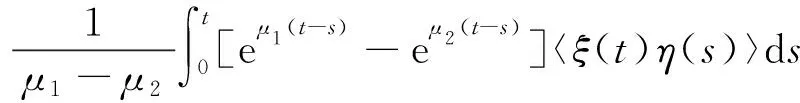
(15)
将式(7)代入式(15)化简得到
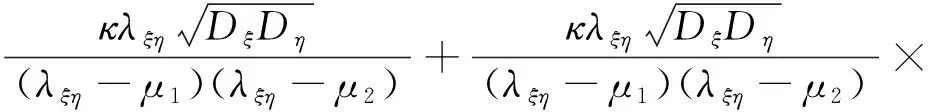
(16)
将式(16)代入式(14)化简后有

(17)
其中,
(18)
联立式(10)和式(17)可得〈x〉和〈ξx〉满足如下的非齐次线性方程组
(19)
式(19)所对应的齐次方程组的特征方程为
λ2+(2a+λξ+Δξ)λ+a(a+λξ+Δξ)-
Dξλξ=0
(20)
由线性方程组稳定性Routh-Hurwitz判据可得如下条件
2a+λξ+Δξ>0,a(a+λξ+Δξ)-Dξλξ>0
(21)
当参数满足式(21)时,线性方程组组的平衡点(0,0)稳定。在此情况下,若双态噪声和白噪声的关联率λξη>max(μ1,μ2), 求解式(19)并令t→∞,可以得到系统的平均稳态响应(一阶稳态矩)的解析表达式为
〈x(t)〉st=Astcos(Ωt+φ)
(22)
式中:Ast和φ分别为系统稳态响应的振幅和相位,满足
(23)
3 随机共振行为研究
式(23)给出了系统的稳态响应振幅Ast解析表达式, 从Ast的解析表达式可知,Ast关于周期激励幅度A, 白噪声强度Dη, 关联系数κ均为单调递增函数。 因此不存在随机共振现象,而关于双态噪声强度Dξ, 相关率λξ, 非对称性Δξ, 两种噪声相关率λξη则可能存在非单调性。 下面我们依次分析Ast关于这些参数存在随机共振现象的条件,并讨论系统参数a和简谐噪声参数对随机共振现象的影响。
3.1 Ast 关于双态噪声强度Dξ 的随机共振
当其他参数固定为常数时,Ast可以看成双态噪声强度Dξ的函数
(24)
式中:
(25)

当系统参数a分别取1.0,0.5,0.2,0.1时, 系统的稳态响应振幅Ast作为双态噪声强度Dξ的函数的曲线图,如图1(a)所示。其他参数设置为A=1,Ω=0.1,κ=0.1,Dη=0.1,λξ=0.1, Δξ=0.1,λξη=0.1,Γ=1,ΩE=0.1。可以Ast关于Dξ出现了随机共振现象, 随着a的不断增加,共振峰不断增高峰值点逐渐右移。Ast作为双态噪声强度Dξ的函数在不同周期激励频率参数下的曲线图,如图1(b)所示。其中,a=0.1,由图1(b)可知,随着周期激励频率的不断减小,共振峰越来越高,且峰值点逐渐左移,这说明对于低频信号会有更明显的共振现象,而且频率越低,越微弱的噪声即能激发共振现象。Ast作为双态噪声强度Dξ的函数在不同阻尼参数Γ和频率参数ΩE情况下的曲线图, 如图1(c)和图1(d)所示。其中,a=1,Ω=0.1,ΩE=0.1(见图1(c)),Γ=1(见图1(d)),从图中可知,随着Γ和ΩE的不断减小,共振峰峰值均不断增大,而共振峰值点始终保持不变,这是因为共振峰值点的位置同Γ和ΩE均无关。

图1 系统的稳态响应振幅Ast作为双态噪声强度Dξ的函数的曲线图Fig.1 The amplitude of the system steady-state response Ast as functions of noise intensity Dξ
3.2 Ast 关于双态噪声相关率λξ 的随机共振
当其他参数固定为常数时,Ast可以看成双态噪声相关λξ的函数
(26)
式中:

(27)
可见Ast关于λξ的单调性与F2(λξ)=Ω2(λξ+γ1)2+(Dξ-a)2(λξ-γ2)2关于λξ的单调性相反, 而dF2/dλξ=2[Ω2+(Dξ-a)2][λξ-[(Dξ-a)2γ2-Ω2γ1]/[Ω2+(Dξ-a)2]],因此记λSR=[(Dξ-a)2γ2-Ω2γ1]/[Ω2+(Dξ-a)2], 可得:当λξ<λSR时,Ast关于λξ单调递增; 当λξ>λSR时,Ast关于λξ单调递减;Ast在λξ=λSR时取到最大值,即出现了随机共振。
当系统参数a分别取0.7,0.5,0.2,0.1时,系统的稳态响应振幅Ast作为双态噪声相关率λξ的函数的曲线图,如图2(a)所示。其他参数设置为A=1,Ω=0.1,κ=0.1,Dξ=1, Δξ=0.1,Dη=0.1,λξη=0.1,Γ=1,ΩE=0.1。从图2(a)可知,Ast关于λξ出现了随机共振现象, 随着a的不断减小,Ast关于λξ的共振峰不断增高且峰值点逐渐左移。Ast作为双态噪声相关率λξ的函数在不同周期激励频率Ω情况下的曲线图, 如图2(b)所示。其中,a=0.5,可以看到随着激励频率的减小,Ast曲线逐渐出现了共振峰,且峰值越来越大,峰值点逐渐右移。Ast作为双态噪声相关率λξ的函数在不同阻尼参数Γ和频率参数ΩE情况下的曲线图,如图2(c)和图2(d)所示。其中,a=0.5,Ω=0.1,ΩE=0.1(见图2(c)),Γ=1(见图2(d)),同样地,随着Γ和ΩE的不断减小,共振峰峰值均不断增大,而共振峰值点始终保持不变。

图2 系统的稳态响应振幅Ast作为双态噪声相关率λξ的函数的曲线图Fig.2 The amplitude of the system steady-state response Ast as functions of correlation ratio λξ
3.3 Ast 关于双态噪声非对称性Δξ 的随机共振
当其他参数固定为常数时,Ast可以看成双态噪声非对称性Δξ的函数
(28)
式中:
δ1=2a+λξ,δ2=[Ω2-a2-(a-Dξ)λξ]/a
(29)
Ast关于Δξ的单调性与F4(Δξ)=Ω2(Δξ+δ1)2+a2(Δξ-δ2)2关于Δξ的单调性相反, 而dF4/dΔξ=2(Ω2+a2)(Δξ-(a2δ2-Ω2δ1)/(Ω2+a2)), 因此记ΔSR=(a2δ2-Ω2δ1)/(Ω2+a2), 可得: 当Δξ<ΔSR时,Ast关于Δξ单调递增; 当Δξ>ΔSR时,Ast关于Δξ单调递减;Ast在Δξ=ΔSR时取到最大值,即出现了广义随机共振。
当系统参数a分别取1.0,0.5,0.2,0.1时,系统的稳态响应振幅Ast作为双态噪声非对称性Δξ的函数的曲线图,如图3(a)所示。 其他参数设置为A=1,Ω=1,κ=0.1,Dξ=1,Dη=0.1,λξ=0.1,λξη=0.1,Γ=1,ΩE=0.1。从图3(a)可知,Ast关于Δξ均出现了随机共振现象, 随着a的不断减小,共振峰不断增高且峰值点逐渐右移。Ast作为非对称性Δξ的函数在不同周期激励频率Ω情况下的曲线图,如图3(b)所示。其中,a=1, 从图3(b)可知,随着激励频率的减小,Ast曲线共振峰峰值越来越大,峰值点逐渐右移。Ast作为双态噪声非对称性Δξ的函数在不同阻尼参数Γ和频率参数ΩE情况下的曲线图, 如图3(c)和图3(d)所示。其中,a=1,Ω=1,ΩE=0.1(见图3(c)),Γ=1(见图3(d)),同样地,随着Γ和ΩE的不断减小,共振峰峰值均不断增大,而共振峰值点始终保持不变。

图3 系统的稳态响应振幅Ast作为双态噪声非对称性Δξ的函数的曲线图Fig.3 The amplitude of the system steady-state response Ast as functions of asymmetry coefficient Δξ
3.4 Ast 关于双态噪声和简谐噪声关联率λξη 的随机共振
当其他参数固定为常数时,Ast可以看成噪声关联率λξη的函数
(30)
式中:
(31)

当系统参数a分别取1.0,0.5,0.2,0.1时, 系统的稳态响应振幅Ast作为关联率λξη的函数的曲线图,如图4(a)所示。其他参数设置为A=1,Ω=1,κ=0.1,Dξ=1,Dη=0.1,λξ=0.1, Δξ=0.1,Γ=1,ΩE=0.1。 从图4(a)可知,Ast关于λξη均出现了随机共振现象, 随着a的不断减小,共振峰不断增高且峰值点逐渐右移。Ast作为关联率λξη的函数在不同周期激励频率Ω情况下的曲线图,如图4(b)所示。其中,a=0.1,从图4(b)可知, 随着Ω的不断减小,共振峰峰值均不断增大,而共振峰值点则不断右移。Ast作为关联率λξη的函数在不同阻尼参数Γ情况下的曲线图,如图4(c)所示。其中,a=1,Ω=1,ΩE=0.1, 从图4(c)可知, 随着Γ的不断减小,共振峰峰值均不断增大,而共振峰值点则不断右移。Ast作为关联率λξη的函数在不同频率参数ΩE情况下的曲线图,如图4(d)所示。其中,a=1,Ω=1,Γ=1, 随着ΩE的不断减小,共振峰逐渐出现,峰值不断增大,而共振峰值点则逐渐左移。

图4 系统的稳态响应振幅Ast作为双态噪声和简谐噪声关联率λξη的函数的曲线图Fig.4 The amplitude of the system steady-state response Ast as functions of correlation rate λξη
4 结 论
简谐噪声是一种普遍存在的准单色噪声,这类噪声和传统随机共振中考虑的白噪声相比,不仅具有传统的刻画指标-噪声强度参数,还具有另外两个新的指标参数,即阻尼参数和频率参数。本文考虑了乘性双态噪声,周期调制简谐噪声共同作用的线性过阻尼谐振子, 通过分析系统稳态响应振幅的共振行为后发现:由于乘性噪声、周期调制噪声和线性系统的协同作用,系统响应的稳态幅值关于多种噪声参数则存在随机共振现象。并且,系统参数a和简谐噪声阻尼及频率参数均可在一定范围内实现对线性过阻尼振子随机共振的有效控制。因此,本文的研究工作充分说明乘性噪声、周期调制简谐噪声和线性系统的协同作用对系统共振行为起着关键的作用,从而为进一步深入研究多种形式色噪声对系统共振行为的影响提供了理论基础,同时也为后续物理、工程的相关应用提供了坚实的理论依据。
参 考 文 献
[ 1 ] 郑志刚. 耦合非线性系统的时空动力学与合作行为[M]. 北京: 高等教育出版社, 2004.
[ 2 ] BENZI R, SUTERA A, VULPIANI A. The mechanism of stochastic resonance[J]. Physical A, 1981, 14(11): 453.
[ 3 ] FAUVE S, HESLOT F. Stochastic resonance in a bistable system[J]. Phys. Lett. A,1983, 97(1): 5-7.
[ 4 ] GITTERMAN M. Classical harmonic oscillator with multiplicative noise[J]. Physical A , 2005, 352(2): 309-334.
[ 5 ] MCNAMARA B, WIESENFELD K. Theory of stochastic resonance[J]. Phys. Rev. A, 1989, 39(9): 4854-4869.
[ 6 ] JIA Y, YU S N, LI J R. Stochastic resonance in a bistable system subject to multiplicative and additive noise[J]. Phys. Rev. E, 2000, 62(2): 1869-1878.
[ 7 ] 张金燕,林敏. 二次方分段双稳系统的随机共振特性及其应用[J]. 振动与冲击, 2015, 34(19): 213-223.
ZHANG Jinyan, LIN Min. Stochastic resonance characteristic of a quadratic segmented bistable system and its application[J]. Journal of Vibration and Shock, 2015, 34(19): 213-223.
[ 8 ] 李晓龙,冷永刚,范胜波,等. 基于非均匀周期采样的随机共振研究[J]. 振动与冲击,2011,30(12): 78-84.
LI Xiaolong, LENG Yonggang, FAN Shengbo, et al. Stochastic resonance based on periodic non-uniform sampling[J]. Journal of Vibration and Shock, 2011,30(12): 78-84.
[ 9 ] FULINSKI A. Relaxation, noise-induced, and stochastic resonance driven by non-markovian dichotomic noise[J]. Phys. Rev. E, 1995, 52(4): 4523-4526.
[10] BERDICHEVSKY V G M. Multiplicative stochastic resonance in linear systems analytical solution[J]. Europhys. Lett., 1996, 36(3): 161-165.
[11] BERDICHEVSKY V G M. Stochastic resonance in linear system subject to multiplicative and addtive noise[J]. Phys. Rev. E, 1999, 60(2): 1494-1499.
[12] CAO L, WU D J. Stochastic resonance in a linear system with signal-modulated noise[J]. Europhys. Lett., 2003, 61(5): 593-598.
[13] ZHANG L, ZHONG S C, PENG H, et al. Stochastic multi-resonance in a linear system driven by multiplicative polynomial dichotomous noise[J]. Chin. Phys. Lett., 2011, 28(9): 090505.
[14] 冷永刚,田祥友. 一阶线性系统随机共振在转子轴故障诊断中的应用研究[J]. 振动与冲击, 2014, 33(17): 2-5.
LENG Yonggang, TIAN Xiangyou. Application of a first-order linear system's stochastic resonance in fault diagnosis of rotor shaft[J]. Journal of Vibration and Shock, 2014, 33(17): 2-5.
[15] JIN Y, XU W, XU M, et al. Stochastic resonance in linear system due to dichotomous noise modulated by bias signal[J]. J. Phys. A, 2005, 38(17): 3733-3742.
[16] 周玉荣,何正友. 相关偏置信号调制噪声和加性噪声驱动线性系统随机共振[J]. 振动与冲击, 2011,30(11): 171-174.
ZHOU Yurong, HE Zhengyou. Stochastic resonance of a linear system with corelated bias signal-modulated noise and additive noise[J]. Journal of Vibration and Shock, 2011,30(11): 171-174.
[17] ZHANG W, DI G. Stochastic resonance in a harmonic oscillator with damping trichotomous noise[J]. Nonlinear Dynamics, 2014,77(4): 1589-1595.
[18] GUO F, ZHOU Y R., JIANG S Q, et al. Stochastic resonance in an over-damped bias linear system with dichotomous noise[J]. Chin.Phys.Lett., 2006, 23(7): 1705.
[19] 靳艳飞, 徐伟, 李伟. 偏置信号调制下色关联噪声驱动的线性系统的随机共振[J]. 物理学报, 2005, 54(11): 5027-5033.
JIN Yanfei, XU Wei, LI Wei. Stochastic resonance for bias-signal-modulated noise in a linear system[J]. Acta Physica Sinica, 2005, 54(11): 5027-5033.
[20] 张路,钟苏川, 彭皓, 等. 乘性二次噪声驱动的线性过阻尼振子的随机共振[J]. 物理学报, 2012, 61(13): 130503.
ZHANG Lu, ZHONG Suchuan, PENG Hao, et al. Stochastic resonance in a over-damped linear oscillator driven by multiplicative quadratic noise[J]. Acta Physica Sinica, 2012,61(13): 130503.
[21] 胡岗.随机力与非线性系统[M]. 上海:上海教育出版社, 1994.
[22] VANDEN B C. On the relation between white shot noise, gaussian white noise, and dichotomic markov process[J]. J.Stat.Phys., 1983, 31(3): 467-483.
[23] 包景东.经典和量子耗散系统的随机模拟方法[M]. 北京: 科学出版社,2009.
[24] 宋艳丽. 简谐噪声激励下FitzHugh-Nagumo神经元的动力学行为[J]. 物理学报, 2010,59(4): 2334-2338.
SONG Yanli. Dynamical behaviour of fitzHugh-nagumo neuron model driven by harmonic noise[J]. Acta Physica Sinica, 2010,59(4): 2334-2338.
[25] 白占武,宋艳丽.简谐速度噪声与简谐噪声环境中谐振子的动力学共振[J]. 物理学报,2007, 56(11): 6220-6223.
BAI Zhanwu, SONG Yanli. The dynamical resonance of a harmonic oscillator coupled to a heat bath with harmonic velocity noise and harmonic noise[J]. Acta Physica Sinica, 2007, 56(11): 6220-6223.
[26] 付海翔,曹力,吴大进,关联噪声驱动系统的一阶数值模拟算法[J]. 计算物理,1999,16(5): 481-488.
FU Haixiang, CAO Li, WU Dajin. A numerical algorithm of first-order for system driven by correlated noises[J]. Chinese Journal of Computational Physics, 1999,16(5): 481-488.
[27] SHAPIRO V E, LOGINOV V M. “Formulae of differentiation” and their use for solving stochastic differential equations[J]. Physical A, 1979, 91(3/4): 563-574.
