基于小波相关性的简支梁桥损伤评估方法

闫宇智， 战家旺， 张 楠， 夏 禾， 李 明， 胡所亭

(1. 北京交通大学 土木建筑工程学院，北京 100044； 2. 高速铁路轨道技术国家重点实验室，北京 100891)

桥梁结构是交通运输系统中的枢纽工程，其健康状态影响着交通系统的正常运转，关系到社会稳定和人民群众的切身利益。随着我国桥梁建设的迅速发展，桥梁垮塌以及桥梁严重受损等工程事故不断发生，造成大量人员伤亡和财产损失[1]。因此桥梁结构的健康状况检测和评估逐渐受到重视，也渐渐成为桥梁工程研究的热门方向[2-3]。

桥梁健康状态评估方法主要分为静力法和动力法两种。其中，基于动力测试的桥梁结构健康状态评估方法因其测试方便、快捷、经济、不需要中断交通等优势而受到越来越多的关注[4-5]。桥梁动力评估方法的基本思想是：以结构损伤前后的位移、速度、加速度等动力响应或者频率、振型、曲率模态等模态参数的变化为基本依据，对结构的健康状态加以评定。

结构损伤动力识别方法可分为无模型损伤识别方法和基于有限元模型的损伤识别方法两种。小波分析法是近些年发展起来的一种无模型损伤识别方法：余竹等[6]对损伤简支梁的位移响应进行连续小波变换，表明可以通过小波变换模极大值确定损伤的位置；Chang等[7]对简支梁的模态振型做Gabor小波变换，由其系数峰值可以检测到裂缝的位置；任东华[8]提出了基于铁路桥墩模态参数小波变换的损伤识别方法。这些方法都是通过小波变换对信号的局部微小变化较为敏感的特性来进行损伤识别的，然而其大多只能对损伤进行定位，并不能达到对损伤定量识别的目的。基于模型修正理论的结构损伤识别方法是发展较为完善的一种基于有限元模型的损伤识别方法：战家旺等[9]利用模态频率和模态振型构造目标函数，对桥梁下部结构的损伤进行定位和定量识别；杨雅勋[10]提出了基于灰关联曲率绝对差的损伤识别指标，并采用简支梁桥数值模型对其进行了验证。这些方法可对结构损伤进行定位和定量识别，然而在实际应用中，识别参数的数量很容易受到振动测试技术的制约。

在上述背景下，本文综合既有模型修正技术和小波分析方法的优势，提出了一种以小波相关性构造目标函数，采用模型修正技术对桥梁结构进行损伤识别的方法。该方法以移动荷载作用下的桥梁位移响应为研究对象，采用先定位后定量的损伤分步识别方法。进一步提出了桥梁损伤边界逼近分析方法，可实现对未知病害的精确定位和损伤程度的精细化识别。

1 小波相关性指数及计算方法

对于桥梁而言，行驶的车辆是其最主要的活载，因此研究移动荷载作用下桥梁的动力响应具有十分重要的意义。假设N个单元的简支梁桥为等截面(EI为常数，损伤位置除外)，恒载质量均匀分布(单位长度梁的质量m为常数)，阻尼为黏滞阻尼，当移动力荷载P(t)以匀速V在损伤梁上移动时(见图1)，梁的运动满足小变形理论并在弹性范围内，此时梁的运动方程可以表示为

(1)

式中：δ为Dirac函数； 位移y(x,t)可根据振型分解法写成广义坐标形式

(2)

式中：qi(t)为第i阶广义振型坐标；φi(x)为第i阶模态振型。从式(2)中可知，当已知结构的各阶模态振型φ(x)， 便可以求得移动荷载作用下简支梁的位移y(x,t)。由位移互等定理[11]可知，移动荷载作用下的位移响应可代替模态振型作为小波变换损伤识别的输入。

图1 移动荷载作用下的简支梁桥Fig.1 Simply-supported bridge under moving loads

由图1可知， 虽然在刚度变化截面a的左右两侧EI(a+)≠EI(a-)，但结构(竖向位移、转角、弯矩和剪力)仍应满足变形协调条件和内力平衡条件

(3)

小波变换是一种信号时频域分析工具，它可以同时在时域和频域内对信号进行分析。小波具有多分辨率的特点，正是这种特性使得小波变换具有对信号的自适应性。由于对信号进行小波变换后求二阶导数等价于用小波函数的二阶导数对信号进行小波变换[12]，因此本文选取满足消失距的墨西哥帽小波(Gauss函数的二阶导数的相反数)作为母小波函数

(4)

对移动荷载作用下结构x0位置处的位移响应时程进行连续小波变换

(5)

式中：ψ*(t)为复共轭；s和u分别为尺度因子和平移因子。由于损伤位置处二阶导数不等，使得信号在损伤位置处发生突变，通过检测突变位置即可对损伤进行定位。

在分析尺度s的选择上，原则上来讲尺度越小越能反映奇异点的局部特性；但是现实中我们往往还需要考虑动力效应和噪声的影响，尺度越小，其小波系数就会越大，对损伤识别结果的干扰也就会越大。综合考虑以上因素，选择合理的尺度范围可更加方便的发现奇异点。

为了对损伤进行定量评估，提出了小波相关性的概念。小波相关性(Wavelet Transform Correlation， WTC)反映了两条不同信号曲线进行小波变换后同一尺度下的相关程度，它对简支梁的刚度矩阵的变换非常敏感。例如，实测简支梁位移在尺度k下的小波系数曲线Wtk与相同尺度下的理论简支梁小波系数曲线Wak之间的WTC指数为

(6)

对于简支梁而言，当有限元模型与实际简支梁结构趋于吻合时，WTC指数计算结果趋近于1；相反当实际简支梁结构发生损伤时，其位移响应的小波系数线Wtk在损伤区域附近会发生明显突变，此时，WTC指数计算结果也将发生变化，损伤程度越大，WTC指数越趋近于0。基于损伤程度和WTC指数的映射关系，即可实现对简支梁损伤的定量评估。

2 基于小波相关性的损伤识别方法

本文在既有模型修正方法的基础上，以移动荷载作用下的桥梁位移响应为研究对象，提出了基于小波相关性的损伤识别方法，其损伤识别流程如图2所示。

图2 简支梁桥健康状态动力评估流程Fig.2 Flowchart of simply-supported bridge dynamic assessment

步骤1对实际桥梁结构施加移动荷载，拾取结构的位移响应，并采用连续小波变换对响应进行分析，得到实际多阶模态频率和多尺度小波系数曲线。

步骤2选取合理尺度的小波系数曲线，对其奇异性进行判别，实现桥梁损伤的定位识别。

步骤3建立有限元模型，对有限元模型施加移动荷载，拾取对应位置处的位移响应，并对其进行重采样处理，使得有限元模型与实际桥梁结构在移动荷载通过时的采样点数保持一致，并得到理论多阶模态频率和多尺度小波系数曲线。

步骤4基于模态频率和WTC指数构造目标函数，通过优化迭代方法识别简支梁结构损伤定位区域的整体状态指数，最终实现桥梁损伤的定量识别。

基于上述损伤识别流程，即可实现简支梁桥多个位置病害的同步定位和分步定量识别。并将其应用于铁路桥梁的损伤评估中。该方法与其他模型修正方法类似，本质上是一种结构优化求解问题。

2.1 桥梁损伤模拟

一般认为损伤并不改变结构的质量，仅改变其刚度。刚度EI因病害发生变化时，一般假定截面惯性矩I不改变，而用降低弹性模量E来模拟。将简支梁模型的全桥弹性模量均分为n个损伤区段，假设E0j为桥梁第j个损伤区段的初始设计弹性模量，Edj为发生病害后该区段的弹性模量， 则第j个损伤区段的损伤指数αj(0≤αj≤1)定义为

(7)

可用上述各损伤区段的损伤指数构成向量来描述简支梁的整体状态指数

α={α1,a2,…,αn}

(8)

通过桥梁整体状态指数的变化，即可对桥梁各个部位的健康状态进行定位和定量评估。

2.2 模型修正优化算法

结构模型修正中，目标函数是描述有限元模型特性与实际结构特性相关程度的表达式，表示模型与实际结构之间的误差。实际结构发生损伤时，测点位移响应的WTC指数会发生明显变化，因此可基于该指标对结构的损伤进行识别。本文采用模型与实际结构的模态频率和WTC指数差值构造目标函数

(9)

式中：λai和λti为桥梁第i阶理论和试验的模态频率值；mf为实测频率的阶数；η1和η2为基于各阶频率的目标函数与基于WTC指数的目标函数在总目标函数中的权重系数，反映了各子目标函数在总目标函数中的相对重要性。

与传统基于模态参数的目标函数相比，该目标函数具有如下特点：

(1) 直接利用有限元模型和实际桥梁结构小波系数曲线的形状相似性，不需要精确的位移幅值，减少了测试误差和噪声的影响。

(2) 对损伤梁进行识别时，仅需在梁上布置一个位移测点即可对简支梁的损伤进行定位和定量识别，操作简单，快捷，准确性高。

(3) 采用先定位后定量的损伤分步识别方法，减少了待识别参数的个数，提高了循环迭代的计算效率。

在进行目标函数匹配时，采用有边界信赖域方法对非线性方程进行求解。收敛准则为

(1)F(α)≤ξ

(10)

(2) |Fk+1(α)-Fk(α)|/Fk(α)≤ε&K>D

(11)

式中：ε(%)为容许误差；ξ为容许残差；D为限定最大迭代次数。两者满足其一即达到收敛。

3 损伤识别数值算例

3.1 桥梁模型

以图3所示简支钢梁模型为研究对象，利用本文所提的改进模型修正方法对其进行损伤识别。简支梁模型材料为钢材，弹性模量为2×105MPa，密度为7 800 kg/m3，泊松比为0.25，跨度为1 900 mm，截面高20 mm，截面宽142.5 mm。移动荷载大小为270 N，移动荷载速度为0.2 m/s，采样频率为512 Hz，模型采用平面梁单元建模，并用降低单元刚度的方法模拟桥梁损伤。

由于小波变换是基于信号奇异性的损伤识别方法，需要对模型进行较为精细的单元划分，较小的单元长度也保证了信号的平稳，因此本文将该简支梁模型划分为51个节点(依次从左到右)，50个单元，单元长度为38 mm。由于模型的单元长度较小，在实际简支梁结构发生损伤时往往会伴随着相邻几个单元同时发生损伤，因此将全桥均分为10个损伤区段，即将相邻5个单元作为整体进行损伤识别。设置的损伤工况如表1所示，位移测点布置在26节点。

图3 简支钢梁有限元模型Fig.3 FE model of simply-supported bridge

工况损伤单元(损伤区段)损伤指数工况131～35单元(E7)0.2工况231～35单元(E7)0.5工况316～20单元(E4)0.5工况416～20单元(E4),31～35单元(E7)0.5,0.2工况531～33单元(部分E7)0.5

模态频率是最容易测量，也是精度最高的模态参数。将各损伤工况下简支梁桥的两阶模态频率汇总于表2。从表2可知：①当损伤发生时，简支梁各阶模态频率均有一定程度的下降，说明模态频率对简支梁的损伤较为敏感，因此将模态频率指标纳入目标函数；②不同损伤区域发生相同损伤程度的情况下，各阶模态频率值相同，说明模态频率仅能确定损伤是否发生，而不能对损伤实现定位和定量识别。

表2 频率汇总

3.2 桥梁损伤定位识别

以损伤工况2为研究对象，对简支梁的损伤进行定位识别，其中横坐标为归一化的荷载位置x/L。图4为桥梁损伤前后移动荷载通过时的位移时程曲线对比图。从图中可以看出，几乎看不出位移响应在损伤位置处有任何突变。

图4 损伤前后位移时程曲线Fig.4 Deflection time histories before and after damage

对损伤梁的位移时程曲线做连续小波变换，得到最大尺度smax=100的小波系数灰度图(见图5)，其中颜色越浅数值越大。从图5可知，在0.6L～0.7L附近灰度图呈白色，说明该区域存在奇异性，即出现损伤。

本文选取尺度s=20作为该简支梁的分析尺度。损伤前后小波系数曲线对比图，如图6所示。从图6可知，与未损伤区域相比，损伤区域的小波系数曲线在损伤位置处会出现明显凸起。

图5 工况2下小波系数灰度图Fig.5 Gray image of wavelet coefficient for case 2

图6 损伤前后小波系数曲线对比图Fig.6 Comparison of wavelet coefficients curve before and after damage

采用上述小波分析方法即可对简支梁桥的损伤进行定位识别。基于损伤前后小波系数曲线的WTC指数，采用模型修正技术，即可对桥梁的损伤进行定量识别。

3.3 桥梁损伤定量识别

将结构在损伤状态下的小波系数曲线和模态频率作为“实测值”，基于图2测试流程计算损伤前后的WTC指数，并结合前2阶模态频率构造目标函数。其中，一阶模态频率、二阶模态频率和WTC指数构造的目标函数的权重系数比值为1∶1∶10。对上节中确定的损伤区域进行损伤识别。识别结果见图7，损伤指数随迭代次数的变化规律见图8。从图中可以看出：①在0.6L～0.7L处确实出现损伤，损伤指数为0.5，与设定损伤值完全吻合；②迭代10次左右损伤指数就达到收敛，计算效率较高。

图7 工况2损伤识别结果Fig.7 Damage identification results for case 2

图8 工况2条件下损伤指数随迭代次数变化规律Fig.8 Damage indexes vs iteration number for case 2

同理，工况1、工况3和工况4下的损伤识别结果，分别如图9～图11所示。从图9～图11可知，在简支梁不同位置设定的不同程度损伤均得到了较为准确的识别。

图9 工况1损伤识别结果Fig.9 Damage identification results for case 1

图10 工况3损伤识别结果Fig.10 Damage identification results for case 3

图11 工况4损伤识别结果Fig.11 Damage identification results for case 4

4 损伤识别影响因素分析

对于实际桥梁而言，一般事先并不知道移动荷载的大小和速度，测点位置及噪声对损伤识别结果的影响也值得关注，因此本节依然以图3简支钢梁模型为研究对象，对基于模型修正理论和小波相关性的简支梁桥损伤识别方法的影响因素进行逐一分析。

4.1 荷载大小对损伤识别结果的影响

为了研究移动荷载大小对损伤识别结果的影响，对损伤模型(工况2)依然施加270 N的移动荷载，对待修正模型分别施加270 N，405 N和540 N三种不同大小的移动荷载，损伤识别结果如图12所示。从图12可知，移动荷载大小对损伤识别结果几乎没有影响。

图12 荷载大小对损伤识别结果影响对比图Fig.12 Influence of load value on damage identification

4.2 荷载速度对损伤识别结果的影响

当移动荷载以不同速度通过简支梁桥，采用相同采样频率所得到的采样点数会有所差别。但在构造WTC指数时，需要损伤模型与待修正模型的位移时程具有相同的采样点数。因此，为了解决该问题又不影响损伤模型位移响应(实测值)的准确性，需对待修正模型的位移响应进行重采样处理。

为了研究移动荷载速度对损伤识别结果的影响，将损伤模型(工况2)的移动荷载速度设为0.2 m/s，将待修正模型的移动荷载速度分别设为0.2 m/s，0.3 m/s和0.4 m/s，损伤识别结果如图13所示。从图13可知，移动荷载速度对损伤识别结果几乎没有影响。但是移动荷载的速度不宜过高，过高的速度会导致结构位移响应的动力成分增加，采样点数减少，信号平稳性下降，最终影响识别的精度。

图13 荷载速度对损伤识别结果影响对比图Fig.13 Influence of load velocity on damage identification

4.3 测点位置对损伤识别结果的影响

对于位移测点来说，不同的测点位置对应不同的

位移时程曲线，因此位移测点的位置对损伤识别结果的影响需要进行详细分析。分别将位移测点布置在13节点(L/4附近)、26节点(L/2附近)和37节点(3L/4附近)，各测点小波系数灰度图及损伤识别结果如图14和图15所示。

从图14和图15可知：①测点离损伤位置越近，灰度图的亮条纹越明显，定位识别效果越好，这是因为由于损伤的存在，损伤位置处的响应有更大的奇异性，因此为了保证各个位置的损伤均能较好定位识别，位移测点尽量布置在跨中附近；②测点位置对损伤的定量识别几乎没有影响。

图14 不同测点响应的小波系数灰度图Fig.14 Gray image of wavelet coefficient in different measuring points

图15 测点位置对损伤识别结果影响对比图Fig.15 Influence of measuring points position on damage identification

4.4 噪声对损伤识别结果的影响

为了分析噪声对识别结果的影响，在测试加速度和位移响应中均加入一定水平的随机噪声，并用“污染”后的数据进行损伤识别。加入3%的随机噪声时工况4的损伤定位识别结果和定量识别结果，分别如图16和图17所示。可以看出，信号中虽然加入了噪声，但是依然能够对损伤进行定位识别和较为精确的定量识别，这说明本文所提的损伤评估方法具有较强的抗噪性。

图16 加入3%噪声后小波系数灰度图Fig.16 Gray image of wavelet coefficient with 3% noise

图17 加入3%噪声后工况4损伤识别结果Fig.17 Damage identification results with 3% noise for case 4

5 桥梁损伤边界逼近识别方法

当实际结构发生损伤时，损伤的位置和程度是无法预知的，而在有限元建模时，单元和损伤区段的划分是随机的，因此并不能够保证损伤区段与实际损伤位置的完美重合。基于此，本文提出一种桥梁损伤边界逼近识别方法，具体步骤如下：

步骤1对移动荷载作用下桥梁的位移响应进行连续小波变换，得到多尺度小波系数曲线图，实现对损伤的初步定位识别。

步骤2采用本文所提有限元模型修正方法对第一步定位的损伤区段进行初步的定量识别。

步骤3对损伤区段进行精细划分，从左右边界逐渐逼近损伤区，最终实现桥梁损伤的精确定位和精细化识别。

5.1 损伤区域定位

仍以图3所示的简支钢梁为例，损伤位置及程度选用工况5。具体损伤单元和损伤区段的划分，如图18所示。对损伤梁的位移时程曲线做连续小波变换，得到的小波系数灰度图，如图19所示。从图19可知，损伤区域初步定位于0.5L～0.8L。

图18 损伤单元和损伤区段划分图Fig.18 Division of damage elements and damage areas

图19 损伤工况5小波系数灰度图Fig.19 Gray image of wavelet coefficient for case 5

5.2 损伤程度初步定量

采用本文所提方法对疑似损伤区段E6，E7和E8进行初步定量识别，结果如图20所示。从图20可以判断：①E6和E8区段的损伤指数较小，固在此区段内未发生明显损伤； ②E7区段的损伤指数较大，说明该区段发生了明显损伤。E7区段的损伤指数识别值为0.37，与假定的0.5有一定的误差，这是因为识别区段(E7)大于损伤区段(31单元～33单元)，所识别的损伤指数是区域平均后的结果。

图20 损伤初步定量识别结果Fig.20 Damage preliminary identification results

5.3 损伤程度精细化识别

为了进一步确认损伤的位置和程度，按照从左右边界逐步逼近的原则，将损伤区段E7进一步细分，此时将31单元、32单元～34单元和35单元划分为E7a，E7b和E7c区段(见图21)。以弹性模量E7a，E7b和E7c的损伤指数作为识别参数，再次进行损伤识别，得到识别结果如图22所示。

从图22可知：①E7a区域(31单元)为损伤发生的左临界点，但是由于损伤的右临界点尚未确定，因此其损伤指数的识别值并不精确；②35单元并未发生损伤。

图21 第一次细分后有限元模型Fig.21 FE model after first subdivision

图22 第一次细分后识别结果Fig.22 Damage identification results after first subdivision

为了找到损伤区域的右临界点，对损伤区段进行进一步细分(见图23)，进一步细分后的识别结果，如图24所示。从图24可知34单元未发生损伤。

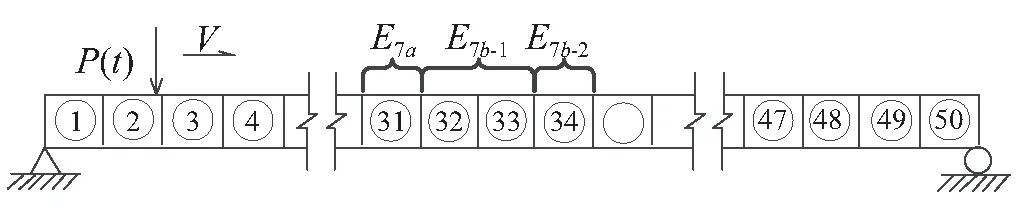
图23 第二次细分后有限元模型Fig.23 FE model after second subdivision

图24 第二次细分后识别结果Fig.24 Damage identification results after second subdivision

如图25所示，对损伤区段再进行细分，细分后识别结果如图26所示。从图26可知，E7b-1b区域(33单元)为损伤发生的右临界点，31单元～33单元的损伤指数均为0.5，与设定值完全吻合。

图25 第三次细分后有限元模型Fig.25 FE model after third subdivision

图26 第三次细分后识别结果Fig.26 Damage identification results after third subdivision

上述分析结果表明，本文所提的损伤分步识别方法可以对损伤逐步逼近，最终实现对损伤的精细化识别。

6 结 论

(1) 提出了一种以移动荷载作用下的桥梁位移响应为研究对象，以小波相关性构造目标函数，采用模型修正技术对简支梁桥进行损伤识别的方法。

(2) 所提方法仅布置一个位移测点即可对不同位置和程度的损伤进行精确识别，且抗噪能力强。

(3) 测点位置距离损伤位置越近，定位识别效果越好；荷载速度、大小和测点位置对损伤的定量识别效果影响较小。

(4) 在实际桥梁测试中，可采用桥梁损伤边界逼近识别方法，实现对损伤位置的逐步逼近和损伤程度的精细化识别。

最后需要说明的是，本文通过理论分析和数值算例初步探讨了基于模型修正理论和小波相关性损伤识别方法的可行性，但在实际应用中的效果尚不清楚。因此，在条件允许的情况下应该进一步开展模型试验和现场试验，对所提方法的实际工程适用性做进一步的验证。

参 考 文 献

[ 1 ] 吉伯海, 傅中秋. 近年国内桥梁倒塌事故原因分析[J]. 土木工程学报, 2010, 43(增刊1): 495-498.

JI Bohai, FU Zhongqiu. Analysis of Chinese bridge collapse accident causes in recent years [J]. China Civil Engineering Journal, 2010, 43(Sup 1): 495-498.

[ 2 ] PEETERS B. System identification and damage detection in civil engineering [D]. Leuven: Catholic University of Leuven, 2000.

[ 3 ] JIANG L J, TANG J, WANG K W. An optimal sensitivity-enhancing feedback control approach via eigenstructure assignment for structural damage identification [J]. Journal of Vibration and Acoustics, 2007, 129(6): 771-783.

[ 4 ] PERERA R, RUIZ A. A multistage FE updating procedure for damage identification in large-scale structures based on multi objective evolutionary optimization[J]. Mechanical Systems and Signal Processing, 2008, 22(4): 970-991.

[ 5 ] 赵俊，张伟伟，马宏伟. 移动荷载作用下简支梁的动态影像及裂纹损伤识别研究[J]. 振动与冲击,2011,30(6): 97-103.

ZHAO Jun, ZHANG Weiwei, MA Hongwei. Dynamic response and crack detection of simply supported beam under moving loads[J]. Journal of Vibration and Shock, 2011, 30(6): 97-103.

[ 6 ] 余竹，夏禾，殷永高，等. 基于小波变换与Lipschitz指数的桥梁损伤识别研究[J]. 振动与冲击,2015,34(14): 65-69.

YU Zhu, XIA He, YIN Yonggao, et al. Bridge damage identification based on wavelet transform and lipschitz exponent[J]. Journal of Vibration and Shock, 2015,34(14): 65-69.

[ 7 ] CHANG C, CHEN L. Vibration damage detection of a timoshenko beam by spatial wavelet based approach[J]. Applied Acoustics, 2003, 64(12): 1217-1240.

[ 8 ] 任东华. 基于模态参数小波变换的铁路桥墩损伤识别方法及试验研究[D]. 北京：中国铁道科学研究院，2014.

[ 9 ] 战家旺，王伟，张楠，等. 基于模型修正理论的铁路桥墩损伤定量评估方法[J]. 中国铁道科学,2015,36(5): 28-35.

ZHAN Jiawang, WANG Wei, ZHANG Nan, et al. Quantitative damage evaluation method for railway piers based on model updating theory[J]. China Railway Science, 2015, 36(5): 28-35.

[10] 杨雅勋. 基于动力测试的桥梁结构损伤识别与综合评估理论研究[D]. 西安：长安大学,2008.

[11] 余竹. 基于移动荷载作用下结构响应及小波分析的桥梁损伤诊断研究[D]. 北京：北京交通大学,2014.

[12] 任宜春，马石城，林琳. 移动荷载作用下梁裂缝识别的小波方法研究[J]. 振动与冲击，2004,23(2): 82-85.

REN Yichun, MA Shicheng, LIN Lin. Identification of simple-supported beam cracks by means of wavelet analysis[J]. Journal of Vibration and Shock, 2004, 23(2): 82-85.