影响三轴数控机床加工精度的因素研究

吴嘉炎

（茂名市高级技工学校，广东 茂名 525000）

数控机床是一种装有程序控制系统的自动化机床，在机械制造业中有着广泛的应用。影响数控机床加工精度的因素有很多，若要保障其的加工精度，我们需要进行科学的研究，采取有效的措施避免加工精度受到影响。基于此，本文就影响三轴数控机床加工精度的因素进行分析。

1 结合多体系统的理论分析齐次坐标在实践运用中的变换情况

1.1 多体系统的理论在三轴数控机床实践方面的运用

在实践工作中，多体系统具有一定的复杂性，尤其是在机械系统中，其主要是通过抽象方式进行有效描述，在当前的实际运用中，已经成为研究机械系统最常用方式。以下通过对系统实施合理编号的方式而抽象出对应的图行表达，可以更好地满足个体位置关系的要求，形成良好的结果，即拓扑结构。

图1是数控机床X、Y和Z型在三维空间中的示意图。

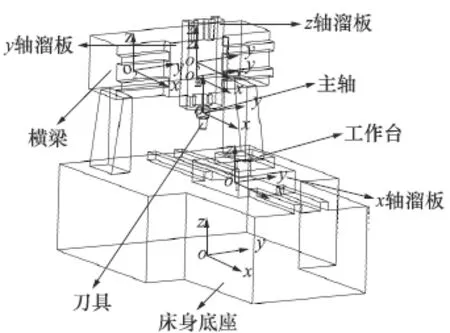
图1 数控机床中X、Y、Z型三维的结构图

在本研究过程中，我们建立三维的空间结构图，即通X、Y和Z，而不同的分支结构构建出拓扑结构，即工件分支以及刀具分支。图2是拓扑结构示意图。

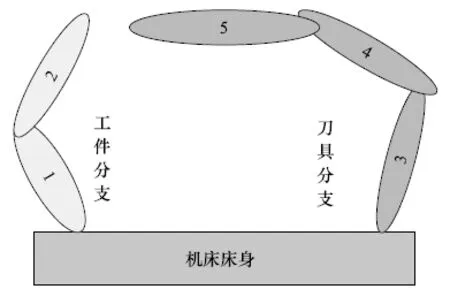
图2 拓扑结构

结合图2中的拓扑结构图可知，主要的两条分支有一定的误差，工件分支的情况是床身1至2，而刀具分支则是床身中的3—4—5属于分支结构。

通过对刀具分支分析可得到：通过图像3和图形4分析可知，y和z分别代表的是溜板，图形5代表的是刀具。

1.2 结合齐次坐标的变换理论分析其实际的应用情况

在齐次坐标中，其实质就是把原本n维向量运用一个+1的维向量进行表示。如，在二维点的(x，y)中，运用齐次坐标就可以将其表示：(nx，ny，n)。所以，此时就可以得到一个齐次向量，而不是唯一的。通过分析齐次坐标可知，n的取值不同，能够表示同一点。如在齐次坐标中的点分别为：(16，8，2)和(8，4，1)，都能够将其表示成一个二维点，即(8，4)。关于齐次坐标系的分析可以参考图3。

结合上图3可知，在坐标系中O1和O2之间有对应的变化情况，通过对坐标系O1的移动可知，即沿x轴方向进行移动，一直达到δx，再沿着y轴方向进行移动，一直到δy，最后向z轴方向继续移动方面则是δz。通过平移之后，在坐标系中就可以通过x、y以及z轴的角度进行旋转而得到角度分别是εx、εy和εz。在坐标系中，O2坐标系O1的换矩阵如下：

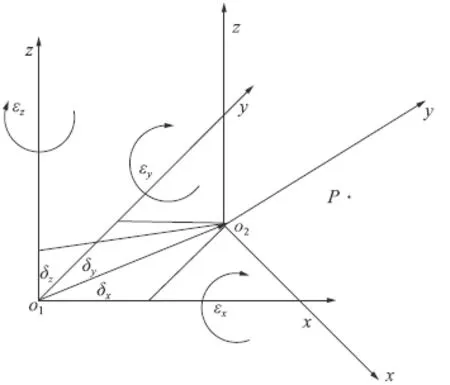
图3 参考坐标系

结合上式可知，Tx、Ty和Tz分别在指坐标系中有不同的指代，即O2至坐标系O1的变化，主要是通过移动以及变换的方式而得到的；而在Rx、Ry和Rz中，分别指代的是O2一直到坐标系O1旋转之后坐标的变换具体情况。

如果位移与旋转角度小的情况下，以及。通过分析可知，二者只能保存一个阶量，同时通过简化就可以得到如下的式子：

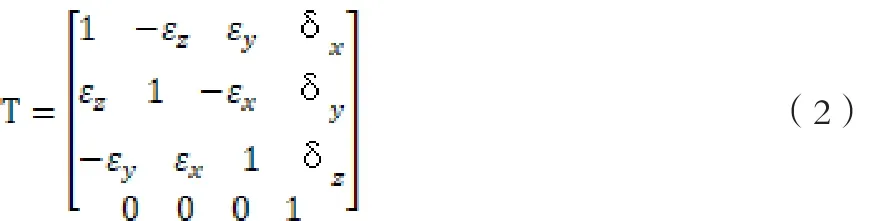
2 结合XYZ型探究数控机床各个不同方面的影响问题

通常情况下，数控机床实施加工，主要需要提升其加工的精度，但是在实践工作中，对加工精度产生的影响因素较多，例如在装配中所可能出现的误差，再如在运行中出现的误差等。此外，热误差、换刀误差也有影响。

2.1 探究数控机床实际装配方面的影响因素

分别通过X、Y和Z型的数控机床，通常在x轴、y轴以及z轴溜板、床身、主轴以及横梁等结合坐标系而做出分析(在选取参考价值方面，主要针对的是刀具、工件而实施加工)。

（1）在机床、床身方面，通过建立一个坐标系进行分析，分别将x、y和z的溜板、主轴、工作台、刀具、横梁和工件建立坐标系。

（2）在建立x、y和z的溜板中，坐标系中的x、y以及z轴的方向可以参考床身底座，并保持和坐标系x、y和z轴的方面是一致的。

（3）在建立x、y和z的溜板中，主要针对工作台、横梁、主轴、底座、刀具以及工件的坐标系分析，其坐标原点是不重合的。

（4）在x、y和z溜板中，主轴、工作台、横梁、工件以及刀具而取出相应点装配，并控制好对应的误差计算。

经过上述分析，工件误差的分支理论变换的矩阵如下：

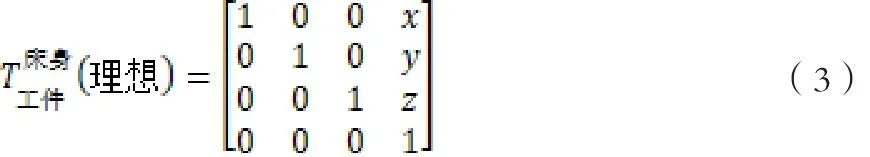
实际装配中发生误差之后，工件误差变换矩阵如下式所示：

在式子中：

在公式中可以将x、y和z分别运用在指代相应的部件，理论坐标差值可以表示为和，移动过程中误差差值；和分别指代的是旋转误差的差值。

通过上述理论可知，刀具误差的分支情况可以转变为实际的变换矩阵：

在公式中，E代表的是综合误差的矩阵。

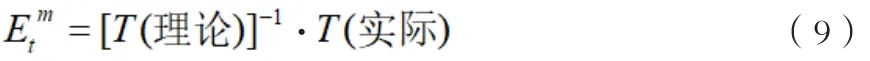
因为这个计算十分复杂，所以在实际的计算过程中将工件的分支以及刀具分支中所存在装配误差的矩阵其表达为公式(10)与(11)。

通过上述装配的误差做出如下的定义：

在上述的公式中可知：⊕代表的是矩阵中包含字母，并且经过应项相加的方式而保障各个不同的常数项不变。

经过上述分析，工件误差的分支理论变换的矩阵如下：

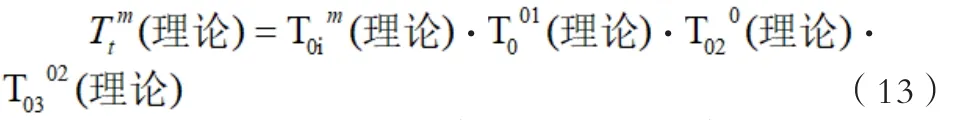
工作加工刀具实际切削点、理论都会发生位置的变化，即偏移的情况。在这种情况下，刀具的坐标系T就会出现对应的改变，而在工件坐标系中的W坐标就可以通过矩阵转换成如下的式子：

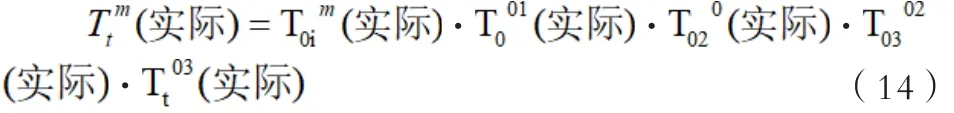
通过进一步的详细分析可知：

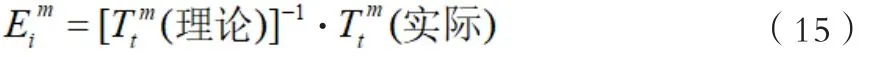
通过小误差的理论可知，将综合的误差矩阵EMT可以表示如下形式：

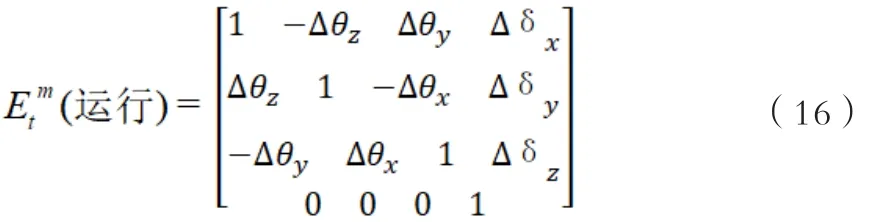
在式中可知：是刀具在坐标系中位置误差：而则作为刀具在坐标系中所出现的误差。

在把不同运动链的过程中，放置坐标的矩阵变换情况可以通过代入后得到和、表达式。

在加工中，数控机床的换刀次数和具体加工工件的情况都有一定的关系，所以，我们假设其对应的数控机床中换刀的次数是n。为了方便计算，就可以取一个合理参考的坐标系，后就分析其换刀一次之后的刀尖理想的位置与实际的位置之间存在的偏差。假设全部换刀后，而x方向中所出现的偏差就会不同，而下标字母则分别代表的是换刀次数；，在换刀之后，y的方向偏差也会变化，而下标字母所代表的换刀次数分别是；，通过换刀之后可知，z方向出现对应的偏差，结合式子可知（下标字母为换刀次数）。最终实施换刀的次数为n次后，x轴方向所发生的偏移量如下所示：

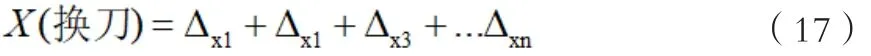
而在换刀n次之后，此时y轴的方向偏移量是：

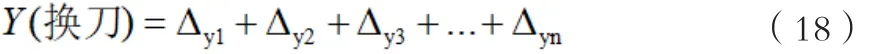
而在换刀n次之后，此时z轴的方向偏移量是：

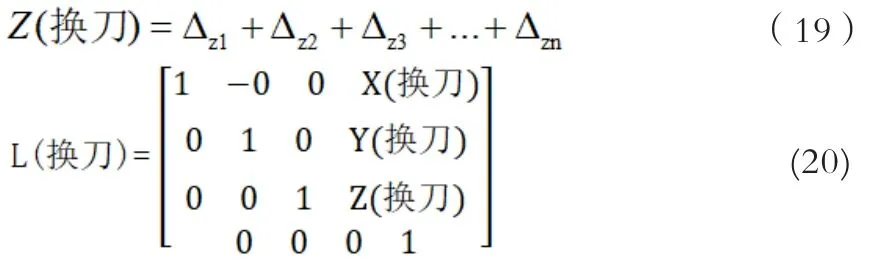
2.2 分析数控机床中温度的影响因素

在加工中，数控机床通过加工时的温度升高，如果在不考虑其他误差的情况，例如几何的误差，其还会产生热误差。 在数控机床中，通过溜板中的x、y和z轴，某一轴的运动产生三个不一样的方向热漂移误差。

（1）溜板在x轴中移动，热漂移的误差是1x( x)、

（2）溜板在y轴中移动，热漂移的误差是1x(y)、

（3）溜板在z轴中移动，热漂移的误差是1x( z)、

下标字母含义是热漂移的误差方向，括号内字母含义是溜板移动的方向。

在这里考虑主轴3个热漂移的误差，记成：。

在工件分支（床身—1—2）中：图形1含义是x溜板，图形2含义是安装x溜板。

刀具分支加工中，图像3含义：y溜板，图形4含义：z溜板，图形5含义是：刀具。

结合数控机床误差分析后，综合的热误差发生矩阵情况，即EMT(热)可以表示为如下方式：

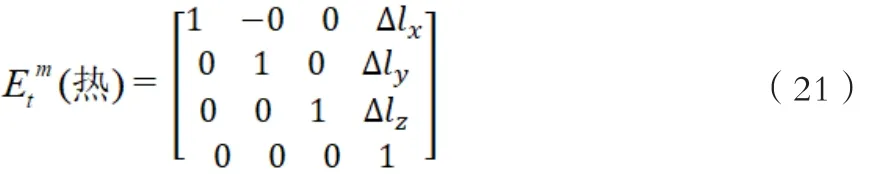
在式子中：

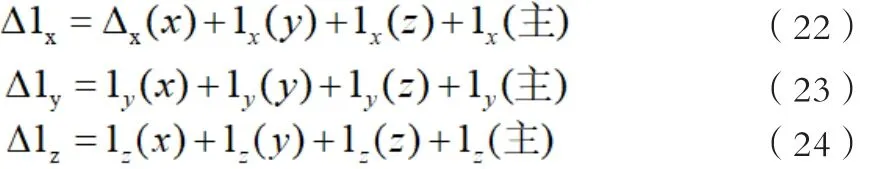
3 结语

通过上述分析可知，数控机床可以凭借自身优点在机械制造业发展过程中得到十分广泛的应用。然而，在日常工作中，数控机床中有许多影响的因素，使加工精度方面受到干扰。应通过研究其中的影响因素，采取措施有效避免发生误差。

[1] 李志鹏.数控机床加工的工艺参数优化与选择[J].现代制造技术与装备,2017,(06):96-97.

[2] 苏显峰.数控机床加工中的精度补偿技术[J].黑龙江科学 ,2017,8(08):72-73.

[3] 王伟,李晴朝,康文俊,陶文坚,杜丽.基于综合评价体系的五轴数控机床加工性能评价和误差溯源方法[J/OL].机械工程学报,:1-9.

[4] 杨斌.基于内置传感器的数控机床动态加工误差测量方法[J].机床与液压,2017,45(01):35-39.

[5] 刘灿,侯磊,马泳涛.非正交五轴数控机床加工整体叶轮的编程工艺研究[J].煤矿机电,2015,(06):45-47.

[6] 程卫锋. 数控机床误差原因和精度补偿[J]. 国防制造技术 ,2016,(02):51-53.

[7] 沈斌,邓丽芬,劳黎露,刘春学.数控机床几何误差测量及误差补偿研究[J].机床与液压,2016,44(05):80-83.

[8] 邹华兵.三轴数控机床几何误差测量与辨识的研究[J]. 制造技