基于模糊集和k-means算法的变压器红外图像分割

， ， ，

(1.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043；2. 中国铁路北京局集团有限公司，北京 100000)

0 引言

k-means 算法是 Mac Queen J提出的一种经典的聚类算法。聚类分析又是数据挖掘中的重要研究领域，广泛应用于数据压缩、模式识别、图像识别、客户分类、空间数据处理等。算法依据经验给出聚类数k值，结果受初始中心影响大，鲁棒性不强。因此有必要对k值的获取进行研究，提高聚类的准确性。

k值的选择，没有固定的选取方法，一般根据具体情况具体分析。文献[1]运用距离代价函数，选取检测距离代价函数最小值时的聚类结果。文献[2]提出一种基于参考区域的初始化方法，用于k-means文本聚类算法自动阈值确定。刘婷等通过评价算法分类程度好坏的适度函数获得k值,并应用人工数据集进行验证[3]。2012年，刘小丹、牛少敏提出结合蚁群算法的分割方法，进行k值获取和聚类中心选定[4]。但由于蚁群算法的自组织性，同时算法复杂、程序运行时间长和易受环境变化的影响，实际应用效果并不理想。2014年，和敬涵等提出基于k-mean聚类的电气设备红外图像故障识别方法[5]，但文中仅仅给出设定k值，分割效果也有待提升，并且成像背景中不含有树木、建筑、电缆、电线杆等复杂背景因素。本文结合红外图像特点，选取用灰度级直方图进行估计。

红外图像具有对比度低、边缘模糊(设备自身热传导，尤其同材质接触情况下更为严重)、信噪比低、成分比较复杂的特点[6]，并且受传感器自身性能影响，不能较好地反应局部细节差异。另外，红外成像因其被动工作，在成像仪感应到的物体表面的红外能量较弱并且在反射干扰(成像仪中会对反射与辐射能量一并计算)等情况下，检测物边缘杂波含量大，使得图像信噪比降低和形状信息不足，也使识别更加困难[7]。因此，根据红外图像自身特点，使用FLUKE TI400热成像仪，现场获取变压器红外数字图像，根据直方图选取k值，然后进行均衡化,调节灰度图像明暗对比度，再结合模糊集理论进行图像增强，更有利于提高k-means算法后续数据的处理，有效提高了分割的准确性。

1 k-means算法原理

k-means算法主要思想是通过迭代过程把数据集划分为不同的类别，并逐次更新聚类中心直至达到要求的精度[8]，下文中将给出具体过程说明与程序流程图。

(1)相似度测度的选择。计算数据相似度时，根据实际需要选择欧氏距离，也可以根据具体情况选择曼哈顿距离或者明考斯距离作为相似性度量[9]。设数据集为X={xm|m=1，2，…，total}，X含有的数据用d个属性A1,A2，…，Ad(维度)来描述。数据样本为xi=(xi1,xi2,…，xid),xj=(xj1,xj2,…，xjd)，其中，xi1,xi2,…，xid和xj1,xj2,…，xjd分别是样本xi和xj对应d个描述属性A1,A2,…，Ad的具体取值。d值越大，相似度越小，反之亦然。欧式距离

(1)

(2)选择评价聚类性能的准则函数。聚类分析是数据挖掘的重要工具，其有效性评价方法选用也各有不同。这里选用误差平方和准则函数作为聚类性能的评价标准

(2)

式中，X为数据集，Xi聚类子集(k个)，mi聚类子集的聚类中心，E为所有对象均方差之和，p为对象的空间中的点。

(3)簇中数据相似度计算。①把所有数据对象随机分配到k个非空的簇中；②计算各个簇的平均值，并用该平均值代表相应的簇；③根据每个数据与聚类中心的距离，分配给最近的簇；④转到步骤②，重新计算各个簇的平均值，新的聚类中心被计算出。不断重复此过程，直到满足准则函数为止。

k-means算法对大数据集挖掘，具有相对可伸缩性，是一种高效的聚类算法[10]。但是k-means算法需要设定初始k值，结果受初始中心影响大，并对“噪声”和孤立点数据敏感，鲁棒性不强。

2 针对红外图像处理改进的k-means算法

2.1 直方图和模糊集的图像增强

红外图像对比度较低，低端热成像产品往往不能兼具良好的温度分辨率与较好的成像质量，而国外高端产品价格昂贵，并且通常降低性能进行出口限制。红外图像对比度低、目标识别与分割较为困难[11]，尤其户外情况下红外成像背景相较于变电站更为复杂，易受天气、阳光反射和“天空陷阱”等因素影响。目前许多研究所与企业都在进行无人机电力巡线开发试验，对户外复杂情况下红外图像的处理，也将更具有实际使用价值。

2.1.1 直方图均衡化

直方图均衡化是一种利用灰度变换，自动调节图像对比度的方法，是一种以累计分布函数变换法为基础的直方图修正法。在低对比度红外图像中应用效果更加明显，如图1，处理后的变压器红外图像目标物轮廓更为清晰。理论关系式为

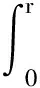
(3)

式中，T(r)为变换函数，T(r)需满足1≥T(r)≥0，pr(r)为图像概率密度函数。数字图像处理中离散形式为

(4)

下面分析变压器红外图像的灰度直方图，由图2(a)可以发现灰度集中分布于灰度级210、230、240附近，低灰度级也存在少部分，因此估计k=3。

图1 红外原始图像增强后效果对比图

2.1.2 基于模糊集的图像增强步骤

(1)图像模糊特征的提取。通过式(5)实现图像空间域到模糊域的变换

(5)

式中，gmn为当前像素点的灰度值；基本参数Fe和Fd为变换系数；gmax为当前图像中最大灰度值。

(2)隶属度修正。 运用模糊增强算子(INT)的回归调用来修正隶属度

(6)

模糊增强是在模糊特征平面上对μmn进行非线性变换，其关键在于用模糊增强算子增大(当μmn≥0.5)μmn的值和减小(当μmn≤0.5)μmn的值。

(3)增强处理后的模糊域逆变换。通过式(7)将图像数据从模糊域逆变换回空间域

(7)

2.2 形态学的开运算

形态学具有完备的数学基础理论，较空域和频域处理也具有明显优势，并且提取边缘光滑、抗噪性好，易用于图像并行处理的实现。通过开运算去除图像中较小的点，并增强图像整体性。

结构元素B对A的开运算，记作AοB：

AοB=(AΘB)⊕B

(8)

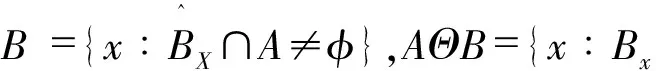
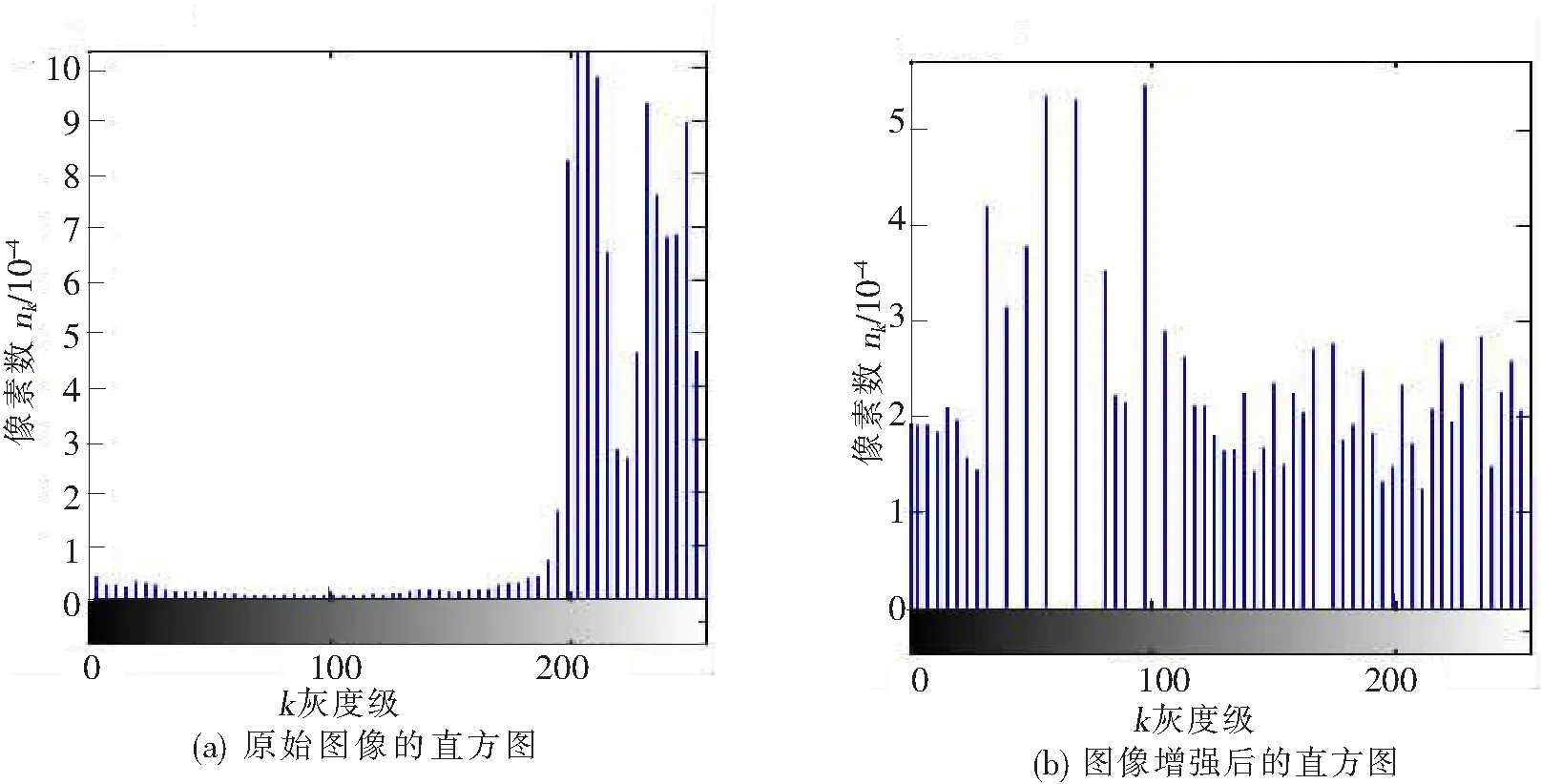
图2变压器红外原始图像与改进后图像的直方图对比图

2.3 算法步骤

(1)根据原始变压器红外图像直方图估计k值。

(2)直方图均衡化、模糊集增强后，为每个聚类确定一个初始聚类中心，这样就有k个初始聚类中心。

(3)将样本集中的样本按照最小距离原则分配到最邻近聚类。

(4)使用每个聚类中的样本均值作为新的聚类中心。

(5)重复步骤(2)、(3)直到聚类中心不再变化。

(6)结束，得到k个聚类，再结合形态学开运算进行细节处理，应用边缘检测进行图像分割。

3 运用Matlab实现算法

在数字图像处理中常应用Matlab或vs2015+opencv进行编程算法改进,其中Matlab也集成了大量内部函数，编写程序比较简单,新版本的opencv已由C语言转向C++/python/C语言开发，开发难度相对较大。在Matlab中通过imhist()函数计算和显示灰度直方图，通过histeq()函数进行直方图均衡化。也可以根据灰度集中分布于灰度级210、230、240附近，取k=3。

图3 改进算法变压器红外图像分割结果对比图

误差概率是一种常见的衡量图像分割结果优劣的加权方法。同样适用于红外图像分割。误差概率可用下式计算

PE=P(O)P(B|O)+P(B)P(O|B)

(9)

式中，P(B|O)是将目标错分为背景的概率；P(O|B)是将背景错分为目标的概率；P(O)和P(B)分别是图像中目标和背景所占比例的先验概率。原始图像分割基本不能判别目标，均衡化后，计算得PE=6.41%。

下面对比几个常用的图像分割评价指标：边界边缘重合度(EBC)、目标分割率(OSP)、分割冗余度(SRR)、分割有效测度(SEM)、dice系数(衡量分割的完整性)。

(10)

式中，B为由边缘检测算子对分割参考图像提取的像素点集合；E为某分割算法分割出边界的像素点的集合。

(11)

式中，RT为真实目标区域；RS为实际结果分割区域。

(12)

(13)

表1 图像分割评价指标

从表1中数据分析图像边缘重合度、目标分割率、分割有效测度、dice系数都有较大提升，分割冗余度(SRR)体现了目标的偏移程度，本文方法在一定程度上使偏移增大，但可以看出增长并不明显,基本可以忽略其对分割效果的影响。

为验证算法的鲁棒性，人为设定k=2,5,10时的原始图像分割结果与改进后分割结果，来做对比分析。从实验结果分析，k=2～9之间都可以较好地分割出变压器，改进后k=2时分割结果更加清晰；k=5时，改进后方法对由变压器底部拍摄到的钢支撑架部分(彩色原图中可以发现支撑钢梁的位置)，也做出了有效分割,并且受物体的发射率及外界光线强度等外部因素影响小。k=9时变压器散热油管也能较好地分割，并且反映了变压箱体温度范围的分布情况。从图4 (m)中明显可以看出4个温度层次，下文将应用smartview软件对变压器温度范围进行温度统计与分析。

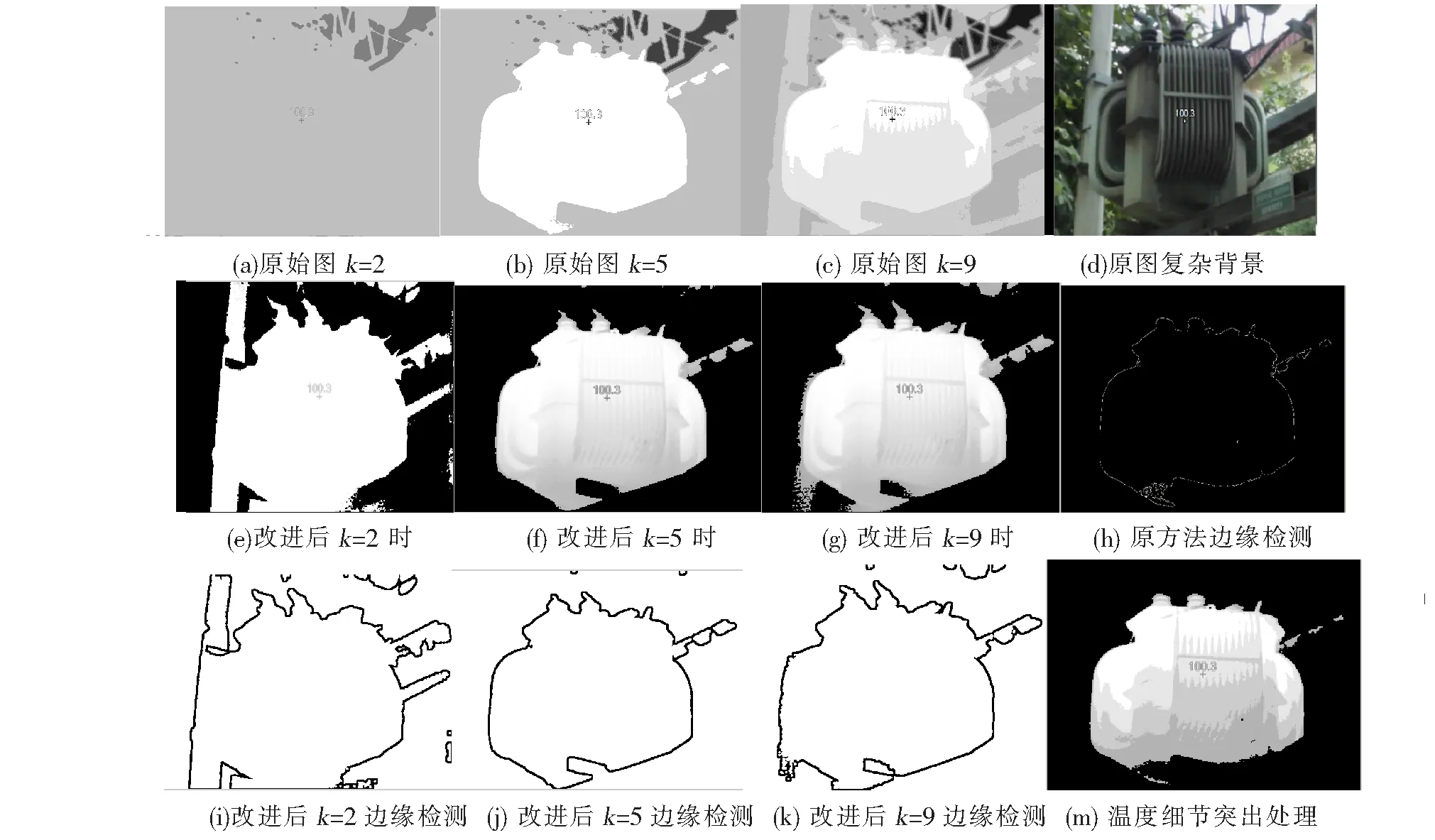
图4 分割结果图与验证算法的鲁棒性分割效果对比图

图5在原始红外图像中标记与统计了部分温度代表点，主要有4个集中分布于温度100.0、96.8、95.5、92.2(°F)附近及背景温度。从k=9的分割图中可以辨别温度区间分布上高下低。为突出变压器温度细节分布，在分割区域内屏蔽模糊增强，增加细节区分度(如图4 (m))。实验中，通过直方图温度统计和3D-IR温度统计图(以三维方式显示像素温度，X与Y轴由图像像素位置组成，Z轴是图像上(X,Y)位置的温度值)验证变压器表面温度分布情况，同时验证了k=9时改进方法的温度细节表现性。若在已分割区域对分割目标，做针对性的细节增强处理，将更好地体现细节区分性，同时也将更好地应用于红外图像的电气设备温度故障判别工作中。

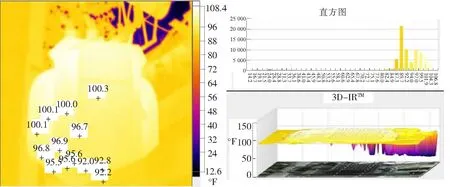
图5 变压器红外图像温度分布标记与综合统计图

4 结论

针对k-means 算法k值选定和复杂背景下红外图像误分割问题，提出了根据灰度级直方图估计k值方法，并利用直方图均衡化和模糊集进行图像增强，然后通过k-means 算法结合数学形态学的开运算，再进行图像分割。通过Matlab编写程序，并与原来算法处理结果比较，表明该改进算法分割更为准确并且鲁棒性好，又使用FLUKE的smartview软件对红外图像中温度分布进行统计，验证了该算法的温度分布细节的表现能力。

参 考 文 献

[1]杨善林,李永森,胡笑旋,等. K-MEANS算法中的K值优化问题研究[J]. 系统工程理论与实践,2006,2:97-101.

[2]索红光,王玉伟. 基于参考区域的k-means文本聚类算法[J]. 计算机工程与设计,2009,2:401-403+407.

[3]刘婷,郭海湘,诸克军,等. 一种改进的遗传k-means聚类算法[J]. 数学的实践与认识,2007,8:104-111.

[4]刘小丹，牛少敏.一种改进的k-means聚类彩色图像分割方法[J]. 湘潭大学自然科学学报，2012,34(2)：90-93.

[5]和敬涵，杨洋，张沛，等.基于k-means聚类旳电气设备红外图像故障识别[C]//中国高等学校电力系统及其自动化专业学术年会论文集.北京：北京交通大学，2014.

[6]顾建雄. 红外图像增强算法研究[D].兰州：兰州大学,2009.

[7]余小英. 云背景下红外弱小目标检测算法研究[D].西安：西安电子科技大学,2009.

[8]任景彪. K-均值聚类算法的研究与分析[D]. 天津：天津工业大学, 2010.

[9]Fahim A M,Salme A M,Torkey F A,et al. An efficient enhanced k-means clustering algorithm[J]. Journal of Zhejiang University Science A:Science in Engineering,2006,10:1626-1633.

[10]Chen Na,Xu Zeshui,Xia Meimei. Hierarchical hesitant fuzzy K-means clustering algorithm[J]. Applied Mathematics:A Journal of Chinese Universities(Series B),2014,1:1-17.

[11]周西柳, 章洁. 基于聚类余弦变换的图像增强算法研究[J]. 计算机仿真, 2012, 29(2):216-219.