计及可再生电源不确定性的配电网鲁棒最优潮流

王婷婷，白晓清，李佩杰，刘文泰

(广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004)

0 引言

随着分布式电源渗透率的增加，配电网的规划与操作将变得更复杂。为了合理规划分布式电源的优化运行，充分发挥具有随机性的可再生分布式电源RDG(Renewable Distributed Generation)等新型电源的积极作用，配电网需采取主动管理、主动规划等措施。传统“被动”配电网将逐渐发展为智能化的主动配电网ADN(Active Distribution Network)[1]。

由于负荷不对称、线路参数不对称及运行条件的改变，三相不平衡是ADN的基本特征之一。因此，许多研究者致力于不平衡配电网潮流研究。文献[2]提出了一种混合相潮流模型，该模型结构复杂，求解效率低。为高效求解不平衡三相模型，2种方法——电流注入法、序分量法被提出[3-4]。文献[5]则基于序分量法，提出一种有效的三相不平衡配电网改进潮流计算方法，该方法收敛率好，通用性强。一般而言，最优潮流(OPF)属于典型的非线性优化问题，呈现非凸性，难以获得全局最优解。为此，二阶锥规划(SOCP)、半定规划等方法被提出[6-7]，例如，文献[8]采用二阶锥松弛技术建立了凸的三相无功优化模型，并调用优化算法包高效求解。同时，ADN中考虑RDG的研究也日益增加。文献[9]考虑风电、光伏发电不确定性，构建了多目标配电网重构模型，采用场景法处理，利用多目标扰动生物地理学算法进行求解。对于分布式电源定容选址问题[10]，为优化利用资源，从考虑网损最小的单目标优化问题发展为综合考虑网损、电压和电流质量等方面的多目标优化问题[11]。然而，以上文献均采用传统的确定性优化DO(Deterministic Optimization)模型和方法，未考虑模型中某些参数的不确定性，如RDG的出力。

由于RDG出力具有较低预测精度及频繁的波动性，其出力往往不确定。这使得线路潮流和节点电压面临越限风险，影响电力系统安全运行。因此，在ADN的相关研究中，RDG出力的随机性不应该被忽略。目前，随机优化SO[12](Stochastic Optimization)和鲁棒优化RO(Robust Optimization)是解决考虑不确定因素优化问题的2种强有力方法。

在SO方法应用方面，文献[13]提出了一个基于机会约束优化并考虑RDG预测误差的多目标三相OPF模型，并用群组搜索及两点估计法求解，该方法计算量大。文献[14-15]基于场景法建立了考虑RDG出力随机性和负荷不确定性的多目标随机优化模型，并利用场景缩减技术减轻计算负担。与上述SO方法相比，RO方法无需建立不确定因素的概率分布模型，采用不确定参量的变化范围来描述不确定性，在不确定性模型构建和计算量方面具有显著优势。目前，RO优化方法大多用于解决主网中考虑参数不确定性的经济调度[16-17]、机组组合[18-19]等问题。由于ADN中优化模型更为复杂，直接应用RO方法存在一定难度。同时，RO方法考虑了不确定参数的最坏情况，获得的解比较保守。而需求侧主动响应可改善电网负荷特性，减少投资，提高运营经济性。其中价格型需求侧响应DR(Demand Response)[20]通过价格信号，引导用户主动调节和改善用电结构与方式，可在一定程度上消纳RDG的不确定性[21-22]。

本文在现有研究成果的基础上，首先基于配电网DistFlow支路潮流SOCP形式，建立以系统利润最大化为目标、考虑需求侧响应的三相不平衡配电网DO-OPF模型；然后对DO模型进行扩展，建立考虑RDG出力不确定性的RO模型，为改善RO模型解的保守性，提高其经济性，本文建立考虑需求侧响应的RO-OPF模型，并对RO-OPF模型中的不确定集进行凸转换，利用凸优化方法求解；最后在2个标准IEEE算例上进行仿真测试研究，对仿真结果进行安全性和经济性比较分析，结果表明，相比于传统DO模型和RO模型，本文所提考虑需求侧响应的RO-OPF模型获得的优化结果能同时兼顾安全性和经济性。

1 不平衡ADN的DO-OPF模型

1.1 三相配电网DistFlow支路等式约束

辐射状配电网结构通常如图1所示。节点i为配电网根节点，P0、Q0分别为流入配电网的有功、无功功率。基于DistFlow方法的支路潮流等式约束详细推导过程见文献[15]，表达式如下：

(1)

(2)

(3)

图1 辐射状配电网结构Fig.1 Structure of radial distribution network

上述等式约束中仅约束式(2)为非凸二次形式，可直接改成SOCP形式[8]：

(4)

其中，‖·‖为2范数。

1.2 ADN三相不平衡DO-OPF模型

一般ADN中较为关注网络损耗、成本等问题，可以归结为考虑经济性最优。不失一般性，本文DO-OPF模型的目标函数设为配电网利润最大化[22]：

maxf(x)=Frev-Fcost

(5)

(6)

运营成本Fcost包括从主网买电费用、可再生分布式能源购买费用、价格型需求侧响应调度互动成本：

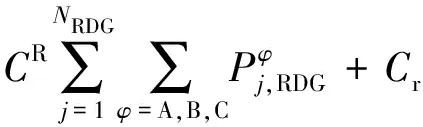
(7)

(8)

(9)

其中，NDR为价格型需求侧响应的数量。

本文DO-OPF模型中考虑以下约束。

b. 电压边界约束：

(10)

c. 主网与配电网间的交换功率限制：

(11)

(12)

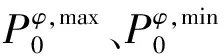
d. RDG运行约束：

(13)

e. 连续无功补偿约束：

(14)

f. 线路潮流约束：

(15)

g. 需求侧响应量约束：

(16)

至此，DO-OPF模型如下：

(17)

2 考虑RDG出力不确定性的RO-OPF模型

2.1 不确定集

模型式(17)中的所有参数均为确定的。然而，由于RDG有功出力预测精度不高，RDG有功出力与预测值的偏差应视为不确定参数。本文采用盒式不确定集描述模型中相应的不确定性参数。

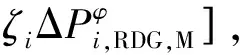
(18)

2.2 ADN三相不平衡RO-OPF模型

(19)

根据式(18)定义，当ΓR=0时，式(19)为DO-OPF模型。显然，当RDG实际出力与预测出力有偏差时，DO-OPF的解有可能不可行。而由于RO-OPF模型中已经考虑了RDG出力不确定性，当此偏差在0.1≤ΓR≤1时依然保持可行，鲁棒性更强。

2.3 RO-OPF模型的求解方法

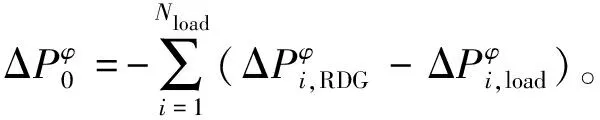
(20)

(21)

其中，Zij为支线ij所在线路总节点数。根据不确定集式(18)，约束式(20)、(21)可分别表示为线性约束式(22)、(23)。

(22)

(23)

其中，∀ζi：‖ζi‖∞≤ΓR；Zij，RDG为节点i至支线ij所在线路末端节点之间所有不确定RDG接入点个数；Zij，DR为节点i至支线ij所在线路末端节点之间所有需求侧响应个数。

(24)

约束式(24)为线性约束且不含任何不确定参数。由不确定集式(18)可知，p为无穷范数，因此对偶‖·‖p*为1范数。同样地，约束式(23)确定性线性约束形式为：

(25)

至此，模型式(19)中所有含不确定参数的约束均已转化为确定的线性约束，所提RO-OPF模型的凸规划SOCP形式为：

(26)

3 算例分析

本文算法在MATLAB仿真平台下进行仿真验证，调用Gurobi求解，以验证本文方法的有效性。在Win7/.NET环境下编译，在PC机(CPU-Intel Core i3 3.19 GHz内存8 G)上分别对IEEE 13和IEEE 123节点标准不平衡三相系统进行测试[25]。

仿真验证过程由如下2个阶段组成。

第一阶段(调度决策制定阶段)：分别对DO-OPF、RO-OPF模型进行求解，得到最优决策(包括头节点出力、需求侧响应量等)，并分析比较经济性。

第二阶段(实际运行/校验阶段)：对各RDG接入点采用蒙特卡洛方法模拟生成符合正态分布的5000 组RDG有功出力，校验第一阶段得出的最优决策的安全性和经济性。采用的校验方法为进行以最优决策量为定值的最优潮流计算，计算收敛表示该最优决策能免疫RDG出力变化，否则采取调用含备用惩罚系数的系统备用方法使其收敛。收敛率高表示在面对RDG实际出力与预测值有出入时，保证系统继续安全运行的能力强。最后对目标函数的期望值和方差进行经济性比较。

仿真流程图如图2所示。

图2 仿真流程图Fig.2 Flowchart of simulation

3.1 基础数据和假设条件

在IEEE 13和IEEE 123节点系统中接入RDG，接入点及其预测值如表1所示。2个系统中RDG渗透率(RDG有功出力与系统总负荷的比值)分别为29.89%、19.43%。其中IEEE 13和IEEE 123节点系统基准功率分别为1 MV·A和10 MV·A，基准电压均为4.16 kV。

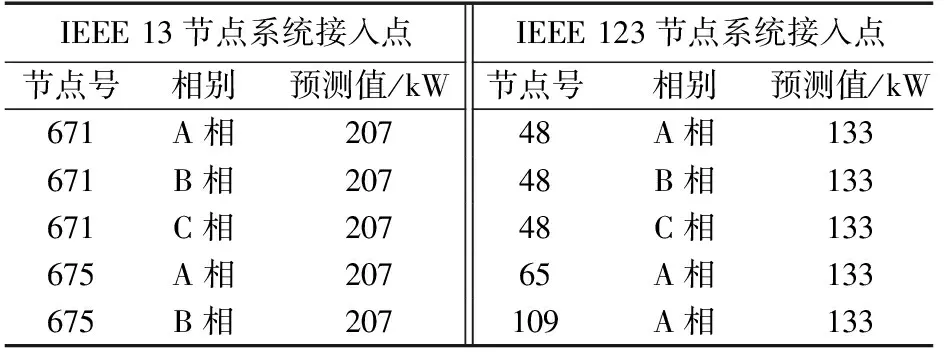
表1 RDG接入点及出力预测值Table 1 Access point of RDG and forecasted power output

单时间断面电价信息如表2所示。选取表3中线路末端负荷节点为价格型需求侧响应，其价格需求侧响应曲线的参数设置见表3。

表2 电价信息表

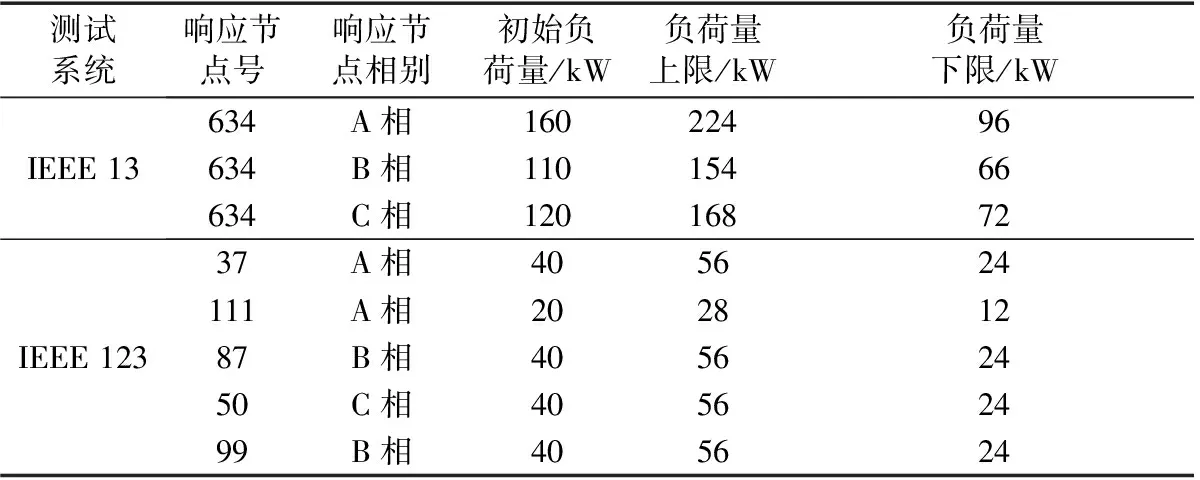
表3 价格型需求侧响应的负荷信息表Table 3 Load information of price-based DR

3.2 模型比较分析

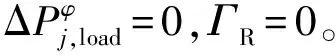
情景3：考虑RDG不确定性及需求侧响应RO-OPF，即模型式(26)。

3.2.1 3种情景第一阶段目标函数经济性比较

单位时间内，IEEE 13节点系统情景1最优解(系统最大利润)为313元，IEEE 123节点系统为300元。

表4展示了随着RDG不确定水平ΓR的增加，相比DO-OPF模型(情景1)，RO-OPF模型(情景2和情景3)第一阶段最优目标函数值的减少百分比。结果表明在调度决策制定阶段，由于考虑了不确定性，RO-OPF模型在2种情景下的经济性均比DO-OPF模型差。当ΓR=100% 时，情景2下IEEE 13节点系统最大利润值减少了17.11%，IEEE 123节点系统减少了13.85%；情形3由于配置了需求侧响应,2个系统的最大利润值减少幅度有所降低，但减少的最大幅度也都超过了6%。此外，IEEE 123节点系统RDG渗透率低，不确定参数较少，因此其RO-OPF最大利润减少幅度比IEEE 13节点系统低。2种RO-OPF场景的目标函数值随ΓR增加而减少，表明RO-OPF的解相比DO-OPF具有一定的保守性。

表4 随着ΓR增大情景2和情景3最优目标函数较情景1的减少百分比Table 4 Optimal objective function decreased percentages of scenario 2 and 3 compared to scenario 1 along with increase of ΓR

表5展示了情景3在不同ΓR下，各需求侧响应节点的各相响应功率计算结果。IEEE 13节点系统在ΓR=100%时达到最大响应量，为10.50 kW，总负荷响应量仅占系统总负荷的0.5%；IEEE 123节点系统最大响应量为ΓR=100% 时的2.06 kW，总响应量仅占总负荷的0.3%。同时，表4中相同ΓR下，情景3的最大利润减少幅度均比情景2的少一半左右。以上结果表明，情景3中引入的价格引导型需求侧响应可以有效改善RO-OPF解的保守性，经济性能较高。

表5 需求侧响应节点互动功率计算结果Table 5 Calculation results of interactive power for DR nodes

根据式(8)需求侧响应量与电价的关系，表6给出各响应节点电价计算结果，并对应表5中各响应节点响应量，电网侧通过向需求侧给出如表6所示的价格信号，使得价格型需求侧响应参与电网互动。

表6 响应节点电价计算结果Table 6 Calculative results of response load price

3.2.2 3种情景所得决策第二阶段安全、经济性比较

a. 第二阶段安全性比较。

表7给出了3种情景在ΓR为10%～100%情况下的成功率比较结果。情景1在所有情况下均有约50%的成功率。同时，随着不确定水平ΓR增大，对情景1第一阶段最优决策进行安全性测试时，OPF计算越难收敛，成功率越低。然而，在情景2和情景3中，2个测试系统成功率均保持100%，即若实际运行中RDG出力预测误差在考虑的不确定范围内时，基于RO-OPF模型所得最优决策不受RDG不确定性的干扰，能保证系统安全稳定运行。与情景1的DO-OPF相比，RO-OPF模型鲁棒性较强，能有效免疫RDG预测误差的不确定性。

表7 随着ΓR增大3种情景的成功率比较Table 7 Comparison of success rates among three scenarios along with increase of ΓR

表8 固定的实验组(不确定性在最坏情况下)及不同ΓR条件下的RO-OPF成功率Table 8 Success rate of RO-OPF for fixed trials (uncertainty at worst case) and different ΓRs

b. 第二阶段经济性比较。

图3 2个系统第二阶段经济性比较散点图Fig.3 Scatter diagram of economy at stage 2 for two systems

系统情景期望值/元均方差/元2IEEE 1310.730.0320.760.0130.820.01IEEE 12310.0620.000 42020.0780.000 13530.0820.000 133

由图3散点图可以看出，2个测试系统中情景3的最大利润值分布整体偏高，且散点呈密集分布。情景2的最大利润值较情景3略低，散点密集程度相差不大，而情景1的5 000个散点值整体偏低，散点稀疏程度高。

表9与图3结果一致，2个测试系统在仿真测试第二阶段(实际运行/校验阶段)RO-OPF模型的目标函数最大系统利润期望值比DO-OPF模型的大，均方差较DO-OPF模型小，而RO-OPF模型中的情景3最大系统利润期望值比情景2大，均方差大致相等。分析表明第二阶段RO-OPF模型所得决策经济性好，能使系统得到较大的最大利润平均值，且系统所得最大利润值数值稳定性好，同时考虑了需求侧响应的RO-OPF模型(情景3)所得决策经济性比未考虑需求侧响应的情景2好。

4 结论

本文提出了一个考虑随机RDG有功出力不确定的ADN的RO-OPF模型，该模型以系统利润最大为目标，同时考虑多个安全约束，并转化成确定性凸规划求解。考虑随机RDG出力不确定性时，RO模型利用合理不确定性水平表示预测误差置信区间，分析结果表明，在调度决策制定阶段RO-OPF模型的经济性较DO-OPF模型略差，最优策略较保守。但在实际运行阶段，RO-OPF模型的最优解展示出较强的鲁棒性，能完全免疫RDG有功出力的不确定性。当在实际运行中RDG出力变化时，RO-OPF所得最优决策依然能保证系统安全运行。同时，由于RO-OPF已经考虑了RDG出力的不确定性，在实际运行阶段不仅减少了不确定因素带来的利润风险，而且能使系统比DO-OPF模型获得较高的利润。此外需求侧响应措施能有效改善RO-OPF解的保守性，提高了其经济性。本文RO-OPF属于单时段优化问题，下一步研究重点会将RO方法引入配电网的动态OPF问题中。

参考文献：

[1] 曾鸣，彭丽霖，王丽华，等. 主动配电网下分布式能源系统双层双阶段调度优化模型[J]. 电力自动化设备，2016，36(6)：108-115.

ZENG Ming，PENG Lilin，WANG Lihua，et al. Two-stage dual-level dispatch optimization model of distributed energy system in active distribution network[J]. Electric Power Automation Equipment，2016，36(6)：108-115.

[2] MARINHO J M T，TARANTO G N. A hybrid three-phase single-phase power flow formulation[J]. IEEE Transactions on Power Systems，2008，23(3)：1063-1070.

[3] GARCIA P A N，PEREIRA J L R，CARNEIRO S J，et al. Three-phase power flow calculations using the current injection method[J]. IEEE Transactions on Power Systems，2000，15 (2)：508-514.

[4] ABDEL-AKHERM，NOR K M. Improved three-phase power-flow methods using sequence components[J]. IEEE Transactions on Power Systems，2005，20 (3)：1389-1397.

[5] 杨雄，卫志农，孙国强，等. 含分布式电源的配电网三相解耦潮流计算方法[J]. 电力自动化设备，2014，34 (3)：99-107.

YANG Xiong，WEI Zhinong，SUN Guoqiang，et al. Decoupled three-phase power flow calculation for distribution network with DGs[J]. Electric Power Automation Equipment，2014，34 (3)：99-107.

[6] JABRR A. A conic quadratic format for the load flow equations of meshed networks[J]. IEEE Transactions on Power Systems，2007，22(4)：2285-2286.

[7] 白晓清，韦化，Katsuki Fujisawa. 求解最优潮流问题的内点半定规划法[J]. 中国电机工程学报，2008，28(19)：56-64.

BAI Xiaoqing，WEI Hua，Katsuki Fujisawa. Solution of optimal power flow problems by semi-definite programming[J]. Proceedings of the CSEE，2008，28(19)：56-64.

[8] 刘一兵，吴文传，张伯明，等. 基于混合整数二阶锥规划的三相有源配电网无功优化[J]. 电力系统自动化，2014，38(15)：58-64.

LIU Yibing，WU Wenchuan，ZHANG Boming，et al. Reactive power optimization for three-phase distribution networks with distributed generators based on mixed integer second-order cone programming[J]. Automation of Electric Power Systems，2014，38(15)：58-64.

[9] 王薪苹，卫志农，孙国强，等. 计及分布式电源和负荷不确定性的多目标配网重构[J]. 电力自动化设备，2016，36(6)：116-121.

WANG Xinping，WEI Zhinong，SUN Guoqiang，et al. Multiobjec-tive distribution network reconfiguration considering uncertainties of distributed generation and load[J]. Electric Power Automation Equipment，2016，36(6)：116-121.

[10] 刘波，张焰，杨娜. 改进的粒子群优化算法在分布式电源选址和定容中的应用[J]. 电工技术学报，2008，23(2)：103-108.

LIU Bo，ZHANG Yan，YANG Na. Improved particle swarm optimization method and its application in the sitting and sizing of distri-buted generation planning[J]. Transactions of China Electrotech-nical Society，2008，23(2)：103-108.

[11] 夏澍，周明，李庚银. 分布式电源选址定容的多目标优化算法[J]. 电网技术，2011，35(9)：115-121.

XIA Shu，ZHOU Ming，LI Gengyin. Multi-objective optimization algorithm for distributed generation locating and sizing[J]. Power System Technology，2011，35(9)：115-121.

[12] 方斯顿，程浩忠，徐国栋，等. 随机最优潮流及其应用的研究综述[J]. 电力自动化设备，2016，36(11)：1-10.

FANG Sidun，CHENG Haozhong，XU Guodong，et al. Reviews on stochastic optimal power flow and its application[J]. Electric Power Automation Equipment，2016，36(11)：1-10.

[13] CAO Y I，TAN Y，LI C，et al. Chance-constrained optimization-based unbalanced optimal power flow for radial distribution networks[J]. IEEE Transactions on Power Delivery，2012，28(3)：1855-1864.

[14] NIKNAM T，ZARE M，AGHAEI J. Scenario-based multiobjective Volt/Var control in distribution networks including renewable energy sources[J]. IEEE Transactions on Power Delivery，2012，27(4)：2004-2009.

[15] 王永杰，吴文传，张伯明. 考虑负荷量测和光伏不确定性的主动配电网鲁棒电压控制[J]. 电力系统自动化，2015，39(9)：138-144.

WANG Yongjie，WU Wenchuan，ZHANG Boming. Robust voltage control model for active distribution network considering load and photovoltaic uncertainties[J]. Automation of Electric Power Systems，2015，39(9)：138-144.

[16] 徐秋实，邓长虹，赵维兴，等. 含风电电力系统的多场景鲁棒调度方法[J]. 电网技术，2014，38(3)：654-661.

XU Qiushi，DENG Changhong，ZHAO Weixing，et al. A multi-scenario robust dispatch method for power grid integrated with wind farms[J]. Power System Technology，2014，38(3)：654-661.

[17] JABR R A. Adjustable robust OPF with renewable energy sources[J]. IEEE Transactions on Power Systems，2013，28(4)：4742-4751.

[18] 高红均，刘俊勇，刘继春，等. 基于坏场景集的含风电机组组合模型[J]. 电力系统保护与控制，2013，41(10)：27-32.

GAO Hongjun，LIU Junyong，LIU Jichun，et al. The unit commit-ment with wind power based on the bad scenario set[J]. Power System Protection and Control，2013，41(10)：27-32.

[19] 汲国强，吴文传，张伯明. 考虑风电不确定性的机组检修鲁棒优化方法[J]. 中国电机工程学报，2015，35(12)：2919-2926.

JI Guoqiang，WU Wenchuan，ZHANG Boming. Robust optimization method of generator maintenance schedule considering[J]. Proceedings of the CSEE，2015，35(12)：2919-2926.

[20] 张钦，王锡凡，王建学，等. 电力市场下需求响应研究综述[J]. 电力系统自动化，2008，32(3)：97-106.

ZHANG Qin，WANG Xifan，WANG Jianxue，et al. Survey of demand response research in deregulated electricity markets[J]. Automation of Electric Power Systems，2008，32(3)：97-106.

[21] 曾丹，姚建国. 应对风电消纳中基于安全约束的价格型需求响应优化调度建模[J]. 中国电机工程学报，2014，34(31)：5571-5578.

ZENG Dan，YAO Jianguo. Optimization dispatch modeling for price-based demand response considering security constraints to accommodate the wind power[J]. Proceedings of the CSEE，2014，34(31)：5571-5578.

[22] NGUYEN D T，NGUYEN H T，LONG B L. Dynamic pricing design for demand response integration in power distribution networks[J]. IEEE Transactions on Power Systems，2016，31(5)：3457-3472.

[23] BEN-TAL A，GHAOUI L E，NEMIROVSKI A. Robust optimi- zation[M]. Princeton，NJ，USA：Princeton University Press，2009：163-179.

[24] JOHAN L. Research article automatic robust convex programming[J]. Optimization Methods and Software，2012，27：115-129.

[25] IEEE PES AMPS DSAS Test Feeder Working Group. 1992 test feeder cases[EB/OL]. [2014-02-03]. http:∥sites.ieee.org/pes-testfeeders/resources/.