电网分区的主动半监督探测方法

刘 剑，李兴源，王 成，干 华，许立雄

(1. 四川大学 电气信息学院，四川 成都 610065；2. 雅砻江流域水电开发有限公司，四川 成都 610051；3. 国网四川省电力公司，四川 成都 610041；4. 成都城电电力工程设计有限公司，四川 成都 610041)

0 引言

负荷需求的增长是电网演化生长的内在动力，其与能源分布在地域上的不匹配，促使现代电网朝着互联的方向发展[1-2]。电网的规模日益庞大、结构日益复杂，对电网的计算分析与运行监控也日益困难。在实际运行中，相关人员通常将互联的大规模电网划分为若干的小规模区域来降低分析调控的复杂度[3-4]。因此，大规模互联电网的快速有效分区具有显著的现实意义。

基于优化的电网分区方法将分区内部联系紧密、分区间联系稀疏的要求量化为目标函数，采用诸如遗传算法[5-6]、模拟退火算法[7]、禁忌搜索算法[8-9]、进化规划算法[10-11]等人工智能优化算法搜索目标函数最优且满足分区内部连通性要求的分区划分方案。优化类电网分区方法难以准确量化定性描述的电网分区要求，且人工智能优化算法具有容易陷入早熟收敛的问题。

自20世纪80年代层次聚类被用于法国电网电压无功控制分区以来，凝聚型电网分区方法得到了更多的研究关注，成为了主流方法[12]。文献[13-15]均以节点间电压无功灵敏度关系定义反映节点间联系紧密性的电气距离，分别采用层次聚类[13]、模糊聚类[14]和仿射传播(AP)聚类[15]进行电网分区。电气距离只给出节点间相异性的量度，并未给出节点坐标的清晰描述，不利于聚类算法的应用[16]。处于同一分区的节点，其对应的图Laplacian矩阵的非平凡特征向量元素十分相似[17]，文献[17-18]取前k个非平凡特征向量构成节点的k个属性，建立节点的坐标描述，继而采用聚类算法完成电网分区。但k值的选取缺乏普适有效的方法。文献[16,19]基于电网的无功控制源构建映射空间，建立节点坐标描述，并且在此基础上应用聚类算法进行电网分区。但是映射空间的维度将随系统规模的增大而增加，易产生“高维聚类问题”[20]。文献[20-21]提出了多阶段的聚类分区方法，初始阶段通过合并电气联系明显紧密的节点集来降低系统的规模，以减少凝聚阶段的聚类维度。凝聚型电网分区方法利用节点之间的某种相似性度量来探测分区，缺少对先验知识的有效利用，当被用于网架结构强度不均匀的互联电网时，难以得到分区半径以及分区数曲线的平坦区[12]，分区结果也难以符合实际应用需求[12]。

为此，本文提出了一种结合主动学习的电网分区半监督探测方法：利用无功电压的局部性和分区内部联系紧密、相互之间联系稀疏的特性，主动选取分区核心节点，将先验知识转化为极少数节点的分区编号标签；基于节点间的电压影响，定义分区对节点的吸引度作为标签扩散的依据，从分区核心节点开始传播标签确定分区划分。此外，借鉴聚类有效性分析的思路，重新定义了silhouettes指标用于评价电网分区结果的优劣。

1 电网分区的主动半监督探测方法

现实网络存在一定的背景，人们对其也有一定的认知。有效地利用这些先验知识可以改善社团(分区)探测结果的质量，使之更加能够符合实际应用需求。但是先验知识往往需要人工转化为社团(分区)探测算法所需的形式，如标签节点，这极大地影响了半监督社团(分区)探测方法的应用。为此，本文引入主动学习的思想，由电力网络演化发展的局域性和电力系统无功电压的局部性等电网先验知识，主动筛选分区的核心节点进行标签标记，从分区核心节点传播扩散分区标签，半监督地探测电网分区。

1.1 分区核心节点的标签主动标记

密度峰值快速搜索聚类CFSFDP[22](Clustering by Fast Search and Find of Density Peaks)是由Alex和Laio提出并于2014年发表在《Science》上的一种高效简洁的聚类算法，可以处理任意形状分布的数据集并且能够自动确定类的个数。CFSFDP的核心是建立在对类中心特性的认知上：类中心具有相对较高的局部密度并且与其他高局部密度数据点之间具有相对较远的距离。电网局域(分区)的中心同样也具有该特性。电力网络的演化发展具有局域性和局域内有限优先连接性[23]：局域电网间，通过少量高压输电线路不断连接逐步形成跨区乃至跨国的互联大电网；局域电网内，变电站将尽可能地选择与中心变电站距离最近的变电站进行接入。局域(分区)中心节点周边线路连接稠密而局域(分区)边界节点周边线路连接稀疏，局域(分区)中心节点具有相对较高的连接稠密度并且与其他高连接稠密度节点间的距离相对较远。为此，可以利用CFSFDP确定类中心的思路来筛选电网分区的核心节点。

CFSFDP采用式(1)所示的高斯核函数来衡量数据点的局部密度ρ。高斯核函数存在明显的拐点，拐点之前函数值大、变化快，拐点之后函数值小、变化慢。

(1)

其中，dij为数据点i和数据点j间的距离；dc为截断距离。

对于任一数据点i，其拐点距离内的数据点越多，则局部密度越大。高斯核函数的拐点界定了数据点局部密度的局部范围。式(1)所示高斯核函数的拐点与输入的截断距离dc密切相关。dc取值的恰当与否决定了最终结果的优劣。电力系统的无功电压具有局部性，节点对其邻域内的节点电压影响显著而对其邻域外的节点电压影响微弱，节点的电压影响呈现类似高斯核函数的分布。但节点的邻域是由电网内在的电气特性所决定的而非外部输入的截断距离dc。故采用节点的电压影响衡量电网节点的连接稠密度，由潮流计算PQ解耦法的电压无功修正方程的系数矩阵B″，可得如下的节点电压影响矩阵z：

(2)

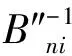
(3)

CFSFDP采用数据点i到所有比其局部密度大的数据点间的距离最小值作为数据点i与其他高局部密度数据点间的距离，即：

(4)

电网节点也采用式(4)来衡量其与其他高连接稠密度节点间的距离，式(4)中的距离dij采用文献[13]中定义的电气距离。

电网分区的核心节点具有相对较高的连接稠密度且与其他高连接稠密度节点间的距离相对较远，即分区核心节点具有较大的ρ值和δ值，将二者相乘得到η，则分区核心节点具有明显大的η值。若对所有节点的η值由大到小排序并作分布曲线图，则曲线存在一个明显间隙，间隙后各节点的η值相差不大，但间隙前节点与间隙后节点的η值差异显著[22]。由此可筛选分区核心节点，进而对其标记分区编号标签，作为先验知识引入指导电网分区探测。

1.2 分区组成节点的标签扩散探测

标签传播社团探测算法的核心思想源自个体在新地方选择居住社区时的反应：个体将选择其大多数直接朋友所居住的社区[24]。直接朋友们的影响造就了该居住社区对个体的吸引。借鉴这一思路，结合电网节点间的电压影响，定义如下的分区k对节点i的吸引度：

(5)

其中，zij为节点电压影响矩阵z的第i行第j列元素，表征节点j对节点i电压的影响；Ck表示第k个分区，|Ck|为第k个分区所包含的节点数。若分区k对节点i的吸引度大于剩余所有分区对节点i的吸引度总和(如式(6)所示)，表明分区k对节点i具有绝对的吸引力，节点i将标记分区k的编号标签。

(6)

位于几个分区结合部的节点j可能无法标记分区编号标签，因为这几个分区都无法表现对节点j的绝对吸引力(不满足式(6))。若节点j本该归属于分区k，则其加入后不会显著破坏分区k内聚外离的结构。对于无法标记的边界节点，可考虑从节点加入分区后对其所加入分区结构破坏的角度来确定节点的分区归属。由电网节点电压影响矩阵z定义如下的分区结构强度：

(7)

其中，Cm表示第m个分区，|Cm|为第m个分区所包含的节点数。式(7)的分子是分区内部对分区节点的电压影响，数值越大表明分区内部连接越紧密，反映了分区的内聚性；分母是分区外部对分区节点的电压影响，数值越小表明分区之间的连接越稀疏，反映了分区的外离性。对边界节点j而言，对比分析其加入各可能分区后所加入分区结构强度的变化，取对分区结构破坏最小或提升最显著的分区加入：

lj=nNo.Ck, ΔγCk=max{γCm-γCm{j}}

(8)

其中，lj为节点j的分区编号标签；nNo.Ck为分区k的编号；γCm{j}为节点j加入Cm前分区结构强度。

综上所述，标签传播的电网分区探测流程可描述如下：

a. 选取标签节点(由1.1节筛选的分区核心节点)的邻接节点作为待标记节点；

b. 由式(5)计算各分区对待标记节点的吸引度；

c. 由式(6)确定是否将分区编号标签传播给分区邻接节点；

d. 统计未标记节点数，若节点数减少则转到步骤a，若无变化表明剩余的未标记节点均为边界节点，则转到步骤e；

e. 确定边界节点的所有可能分区，由式(7)和式(8)标记边界节点的分区编号标签。

1.3 算法流程

电网分区的主动半监督探测(ASD)流程如图1所示。

图1 电网分区的主功半监督探测流程Fig.1 Flowchart of active semi-supervised detectionfor power grid partition

2 电网分区结果优劣的评价

一个好的分区划分结果下各个分区内部节点之间的联系紧密、各个分区之间节点的联系稀疏。这与聚类分析中对聚类结果的评价相一致：一个好的聚类结果下各类内部成员之间的相似度高而各类之间成员的相似度低。针对聚类结果的有效性评价，已有研究提出了众多的量化指标[25]。可从这些指标的评价思路出发，结合电网分区问题本身，重新定义指标的计算式，用于评价电网分区结果的优劣。

文献[25]对30个聚类有效性指标进行了对比分析研究，结果显示silhouettes指标的性能最优。假设有N个样本，d(i，Ck)表示第i个样本与第k类内部各成员样本的平均相似度，silhouettes指标定义如下[26]：

(9)

(10)

silhouettes指标从类内凝聚度a(i)和类间分离度b(i)2个方面综合评价聚类结果，类内凝聚度和类间分离度是基于个体之间的相似性d(i,Ck)来度量的。电网分区同样要求分区内有高的凝聚性而分区间有高的分离性，但这种凝聚性和分离性反映在节点之间联系的紧密程度上。对于节点i而言，若其与节点j联系紧密，则其对节点j的影响大，其受到节点j的影响也大，反之亦然。由电网节点电压影响矩阵z定义如下节点i受第k个分区内部节点的平均影响：

(11)

则用于评价电网分区结果的silhouettes指标如下：

(12)

se的值域为[-1，1]，数值越大表明电网分区结果越好。

3 算例分析

3.1 IEEE 39节点系统

IEEE 39节点系统共有9个电源节点、30个负荷节点(节点39是外部等值节点且负荷功率大于发电功率，将其作为非电源节点)、46条支路。

由式(3)计算IEEE 39节点系统各负荷节点的连接稠密度ρ，并由大到小排序，节点6的连接稠密度最大，为分区核心节点；其余节点还需由式(4)计算距离δ，再由ρ与δ的乘积η做进一步的筛选。图2给出了IEEE 39节点系统除节点6之外其余各负荷节点η由大到小排序后的分布图。图2中曲线存在明显的分割间隙，该间隙之后各节点的η相差不大，但该间隙之前节点(节点16、节点2)的η显著较大。这些节点(节点16、节点2)有相对较高的连接稠密度且与其他高连接稠密度节点有相对较远的距离，为分区核心节点。

图2 节点η值降序曲线Fig.2 η in decreasing order of nodes

由此可确定IEEE 39节点系统的分区核心节点为节点6、节点16和节点2，相应地，系统可划分为3个分区。由分区核心节点按1.2节所述标签扩散方法探测IEEE 39节点系统的分区结果如图3所示。

图3 IEEE 39节点系统分区结果Fig.3 Power grid partition result of IEEE 39-bus system

图4 基于HC方法的IEEE 39节点系统聚类过程Fig.4 Clustering process of IEEE 39-bus system based on HC method

进一步地，采用文献[13]的层次聚类(HC)方法和文献[18]的谱聚类(SC)方法对IEEE 39节点系统进行分区，并与本文所提主动半监督探测方法方法进行比较。

文献[13]中HC方法通过分析聚类过程的合并距离曲线来确定最佳分区个数。图4给出了IEEE 39系统聚类过程的合并距离曲线，图中σ为聚类过程中每次合并的2个类对应的类间距离。图中7分区到6分区、6分区到5分区、5分区到4分区、3分区到2分区均出现明显的平台期，其中3分区到2分区的平台期最长。进一步根据式(12)计算2—7分区的评价指标se，结果如图5所示。3分区方案的se最大，表明3分区方案是最佳的分区结果，因此取3分区方案作为最终的分区结果。

图5 基于HC方法的不同分区方案的seFig.5 se of different partition schemes based on HC method

图6 基于SC方法的相对特征值间隙Fig.6 Relative eigengaps based on SC method

文献[18]中SC方法采用图Laplacian矩阵特征值的相对间隙来确定最优分区数。图6给出了IEEE 39节点系统基于输电线路电抗的Laplacian矩阵特征值的相对间隙，图中γ为Laplacian矩阵特征值的相对间隙，k为分区个数。图中特征值的相对间隙在k=3处取得最大值，由此可确定IEEE 39节点系统的最佳分区数为3。

本文所提主动半监督探测方法确定的分区个数与文献[13]中HC方法和文献[18]中SC方法的结果相一致，表明了所提方法的有效性。

表1为本文所提主动半监督探测方法与文献[13]中HC方法和文献[18]中SC方法的分区结果比对。表1中的节点编号与图3中节点编号相一致。本文所提主动半监督探测方法的分区结果se指标最大，表明所提方法能够获得比HC方法和SC方法更好的分区结果。

表1 不同方法分区结果比较Table 1 Comparison of partition results among different methods

图7为本文所提方法与文献[13]中HC方法各自结果的分区半径比较，图中r为分区半径(分区内部各节点到分区核心节点的平均电气距离)。本文所提方法得到的各分区半径差异显著，这在一定程度上表明IEEE 39节点系统是一个网架结构强度不均匀的系统。HC方法结果的各分区半径差异不大，也说明其聚类过程采用的是同一分区半径，对于网架结构强度不均匀的系统并不能给出符合实际应用需求的分区结果[12]。上述结果表明本文所提方法能够克服凝聚型电网分区方法[13,16,18-19]的不足，具有一定的优越性。

图7 主动半监督探测方法和HC方法分区半径对比Fig.7 Comparison of partition radius between ASD method and HC method

3.2 某实际省级电网

某实际省级电网某时刻实时数据对应的地理接线图(220kV及以上电压等级)如图8所示。该时刻全网共有500 kV节点55个、输电线路67条(不计多回)，220 kV节点316个、输电线路360条(不计多回)。采用本文所提方法对该时刻电网进行分区。

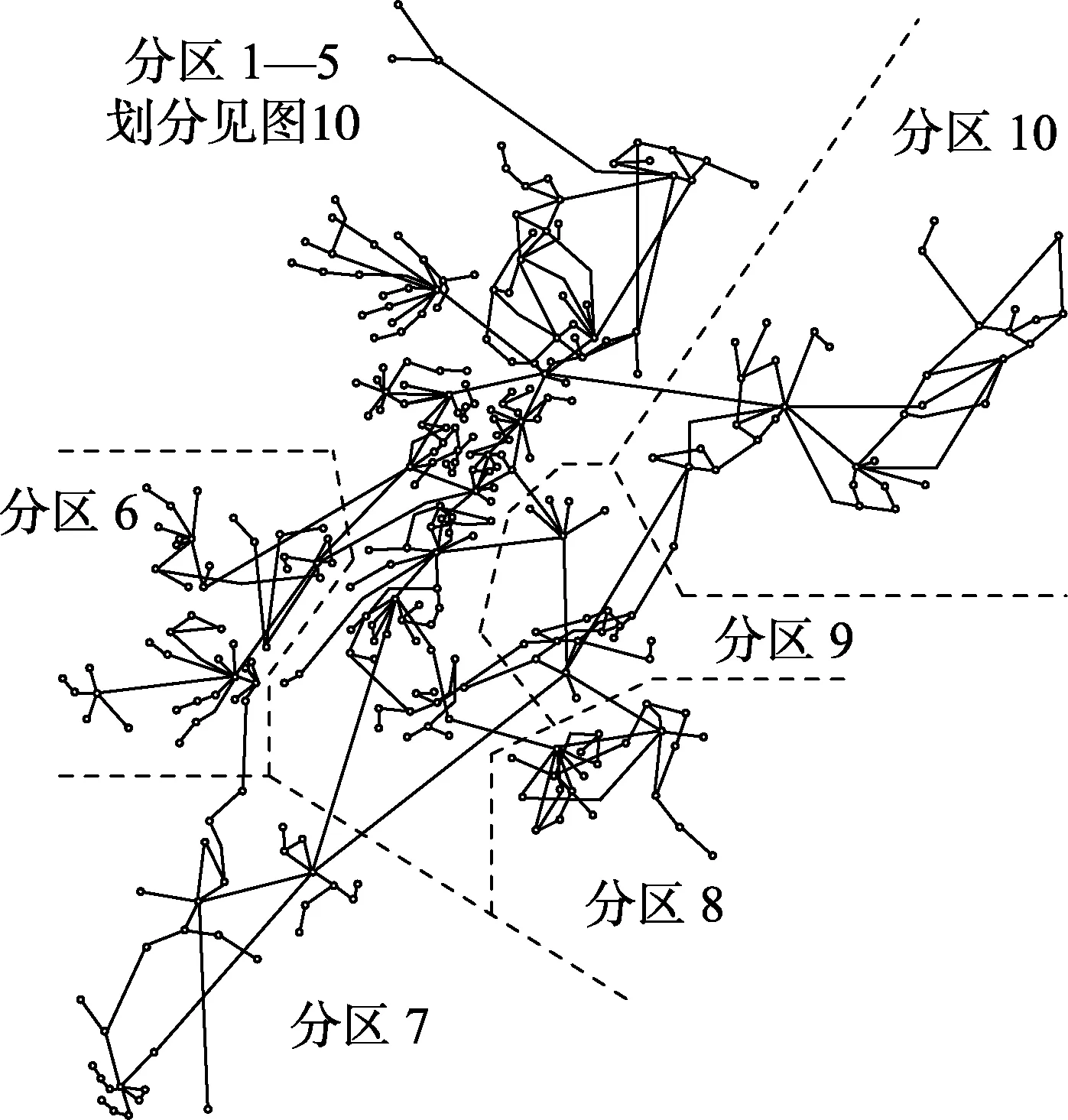
图8 某实际省网分区结果Fig.8 Partition result of a practical provincial power grid

首先，筛选分区核心节点标记分区编号标签。由式(3)计算该省级电网各负荷节点的连接稠密度ρ并由大到小进行排序，连接稠密度最大的节点为分区核心节点之一；对剩余节点由式(4)进一步计算距离δ及ρ与δ的乘积η，并对η由大到小进行排序。图9为该省级电网除了连接稠密度最大节点之外的剩余各负荷节点η由大到小排序后的分布图。图9中的曲线存在一明显间隙，在该间隙之前的节点η明显大于该间隙之后的节点η，且该间隙之后的节点η相差不大。该间隙之前的这些节点具有相对高的连接稠密度且与其他高连接稠密度节点有相对远的距离，为分区核心节点。由此确定出该省级电网有10个分区核心节点，相应地可划分为10个分区。

图9 某实际省网节点η值的降序曲线Fig.9 η in decreasing order of nodes in a practical power grid

然后，传播分区编号标签探测分区组成节点。由分区核心节点按1.2节所述标签传播扩散方法探测该省级电网的分区，结果如图8、10所示。

图10 某实际省网局部分区结果Fig.10 Partial partition result of a practical provincial power grid

分区结果与该省级电网的演化发展和运行实际相符合。分区1和分区5—7在该省级电网形成前分别为西部局域电网和西南部与中南部地区电网。分区1、6、7位于该省西部，水电资源丰富，但受限于地理条件，仅由极少的500 kV输电线路与主网相连(如分区1仅由双回500 kV输电线路与主网相连)。分区5位处该省西部水电基地与东部外送之间，汇集水电分流外送，受限于短路电流问题，在保证水电外送的前提下尽量减少与主网的连接。故西部局域电网和西南部与中南部地区电网各自形成为1个分区。分区2— 4、分区8和9以及分区10在该省级电网形成前分别为北部局域电网、南部局域电网和东部局域电网。分区3、4是该省省会所在也是负荷中心，受限于不断增长的短路电流水平，先从北部局域电网解环运行，然后内部又东(分区3)西(分区4)解环运行，故北部局域电网划分成3个分区(分区2— 4)。分区8和9分别有直流外送和交流外送，考虑到外送安全问题，分片解环运行，故南部局域电网划分成2个分区(分区8和9)。

上述结果表明本文所提方法能够得到符合实际应用需求的分区结果，进一步验证了所提方法的有效性和实用性。

4 结论

本文提出了一种标签节点主动选取的标签扩散电网分区探测方法。利用电网分区核心节点具有相对较高的连接稠密度且与其他高连接稠密度节点间的距离相对较远的特性，主动选取标签节点；依照分区对节点电压的影响，由分区核心节点向分区邻接节点扩散传播标签，探测电网分区。IEEE 39节点系统和某实际电网算例表明本文所提方法能够克服聚类型电网分区方法的不足，有效处理网架结构强度不均匀的情形且无需人工辅助即可确定分区个数。本文所提方法可用于电压无功控制、输电断面识别等。

参考文献：

[1] BATTAGLINI A，LILLIESTAM J，BALS C，et al. The supersmart grid[R]. Postdam,Germany：Postdam Institute for Climate Impact Research，2008.

[2] 周孝信，陈树勇，鲁宗相. 电网和电网技术发展的回顾与展望——试论三代电网[J]. 中国电机工程学报，2013，33(22)：1-11.

ZHOU Xiaoxin，CHEN Shuyong，LU Zongxiang. Review and pros-pect for power system development and related technologies：a concept of three-generation power systems[J]. Proceedings of the CSEE，2013，33(22)：1-11.

[3] 江木，吴文传，张伯明，等. 省级电网分层分区有功实时调度模型与方法[J]. 电力系统自动化，2009，33(22)：10-13.

JIANG Mu，WU Wenchuan，ZHANG Boming，et al. A multi-area coordinated power dispatch method for provincial power grid[J]. Automation of Electric Power Systems，2009，33(22)：10-13.

[4] WANG F,HEDMAN K W. Dynamic reserve zones for day-ahead unit commitment with renewable resources[J]. IEEE Transactions on Power Systems,2015,30(2)：612-620.

[5] DING H,EL-KEIB A A,SMITH R. Optimal clustering of power networks using genetic algorithms[J]. Electric Power Systems Research,1994,30(3)：209-214.

[6] 胡泽春，王锡凡，王秀丽，等. 用于无功优化控制分区的两层搜索方法[J]. 电网技术，2005，29(24)：37-41.

HU Zechun，WANG Xifan，WANG Xiuli，et al. A two-layered network partitioning approach for optimal reactive power dispatching[J]. Power System Technology，2005，29(24)：37-41.

[7] HABIBALLAH I O,IRVING M R. Multipartitioning of power system state estimation networks using simulated annealing[J]. Electric Power Systems Research,1995,34(2)：117-120.

[8] CHANG C S,LU L R,WEN F S. Power system network partitioning using Tabu search[J]. Electric Power Systems Research,1999,49(1)：55-61.

[9] 刘大鹏，唐国庆，陈珩. 基于Tabu搜索的电压控制分区[J]. 电力系统自动化，2002，26(6)：18-22.

LIU Dapeng，TANG Guoqing，CHEN Heng. Tabu search based network partitioning for voltage control[J]. Automation of Electric Power Systems，2002，26(6)：18-22.

[10] COTILLA-SANCHEZ E,HINES P D H,BARROWS C,et al. Multi-attribute partitioning of power networks based on electrical distance[J]. IEEE Transactions on Power Systems,2013,28(4)：4979-4987.

[11] 颜伟，高峰，王芳，等. 考虑区域负荷无功裕度的无功电压优化分区方法[J]. 电力系统自动化，2015，39(2)：61-66.

YAN Wei，GAO Feng，WANG Fang，et al. An optimal network partitioning algorithm for reactive power and voltage control considering regional reactive power margin[J]. Automation of Electric Power Systems，2015，39(2)：61-66.

[12] 李卫星，齐士伟，牟晓明，等. 基于节点耦合关系解析的无功电压递归切割分区方法[J]. 中国电机工程学报，2014，34(31)：5625-5632.

LI Weixing，QI Shiwei，MOU Xiaoming，et al. A recursive network partitioning method for reactive power/voltage control based on the analysis of node coupling relationships[J]. Proceedings of the CSEE，2014，34(31)：5625-5632.

[13] LAGONOTTE P，SABONNADIERE J C，LEOST J Y，et al. Struc-tural analysis of the electrical system：application to secondary voltage control in France[J]. IEEE Transactions on Power Systems，1989，4(2)：479-486.

[14] 乔梁，卢继平，黄蕙，等. 含风电场的电力系统电压控制分区方法[J]. 电网技术，2010，34(10)：163-168.

QIAO Liang，LU Jiping，HUANG Hui，et al. Voltage control partitioning for power containing grid-connected wind farms[J]. Power System Technology，2010，34(10)：163-168.

[15] 周琼，贠志皓，丰颖，等. 风电接入下基于AP聚类的无功功率-电压控制分区方法[J]. 电力系统自动化，2016，40(13)：19-27，158.

ZHOU Qiong，YUN Zhihao，FENG Ying，et al. Reactive power-voltage control partitioning of wind power integration system based on affinity propagation clustering[J]. Automation of Electric Power Systems，2016，40(13)：19-27，158.

[16] 郭庆来，孙宏斌，张伯明，等. 基于无功源控制空间聚类分析的无功电压分区[J]. 电力系统自动化，2005，29(10)：36-40.

GUO Qinglai，SUN Hongbin，ZHANG Boming，et al. Power network partitioning based on clustering analysis in Mvar control space[J]. Automation of Electric Power Systems，2005，29(10)：36-40.

[17] 许刚，王紫雷. 基于Normal 矩阵谱平分法的快速电压控制分区[J]. 电网技术，2014，38(1)：199-204.

XU Gang，WANG Zilei. Fast voltage control partitioning based on Normal matrix spectral bisection method[J]. Power System Technology，2014，38(1)：199-204.

[19] 赵晋泉，刘傅成，邓勇，等. 基于映射分区的无功电压控制分区算法[J]. 电力系统自动化，2010，34(7)：36-39，56.

ZHAO Jinquan，LIU Fucheng，DENG Yong，et al. Network partitioning for reactive power/voltage control based on a mapping division algorithm[J]. Automation of Electric Power Systems，2010，34(7)： 36-39，56.

[20] 韦钢，李明，卢炜，等. 充放储一体站并网的多级阶梯电压控制分区方法[J]. 中国电机工程学报，2015，35(15)：3824-3831.

WEI Gang，LI Ming，LU Wei，et al. Multistage ladder voltage control partitioning method containing grid-connected charging-discharging-storage integrative station[J]. Proceedings of the CSEE，2015，35(15)：3824-3831.

[21] 鲍威，朱涛，赵川，等. 基于聚类分析的三阶段二级电压控制分区方法[J]. 电力系统自动化，2016，40(5)：127-132.

BAO Wei，ZHU Tao，ZHAO Chuan，et al. A three-stage network partition method for secondary voltage control based on agglomerative analysis[J]. Automation of Electric Power Systems，2016，40(5)：127-132.

[22] RODRIGUEZ A,LAIO A. Clustering by fast search and find of density peaks[J]. Science,2014，6191(344)：1492-1496.

[23] 梅生伟，龚媛，刘峰. 三代电网演化模型及特性分析[J]. 中国电机工程学报，2014，34(7)：1003-1012.

MEI Shengwei，GONG Yuan，LIU Feng. The evolution of three-generation power systems and characteristic analysis[J]. Procee-dings of the CSEE，2014，34(7)：1003-1012.

[24] BAGROW J P，BOLLT E M. Local method for detecting communities[J]. Physical Review E，2005，72(4)：046108.

[25] ARBELAITZ O，GURRUTXAGA I，MUGUERZA J，et al. An extensive comparative study of cluster validity indices[J]. Pattern Recog-nition，2013，46(1)：243-256.

[26] ROUSSEEUW P J. Silhouettes：a graphical aid to the interpretation and validation of cluster analysis[J]. Journal of Computational and Applied Mathematics，1987，20：53-65.