随机交叉全局和声搜索算法
2018-06-26翟军昌秦玉平
翟军昌,秦玉平
1.渤海大学 信息科学与技术学院,辽宁 锦州 121013
2.渤海大学 工学院,辽宁 锦州 121013
1 引言
受音乐创作中乐师根据经验调音现象的启发,Geem等人提出了一种新的启发式优化算法和声搜索(Harmony Search,HS)[1]。与一般启发式优化算法[2-6]相比,HS算法种群规模小故内存开销较小,而且每次迭代只产生一个候选和声向量,提高了算法的灵活性。此外,HS算法不需要对求解问题进行编码等操作。HS算法参数较少,具有非常好的优化效果,因此在工程中得到了广泛的应用[7-8]。
HS算法在进化后期容易盲目搜索,不能有效调整解向量的结构。如果算法产生质量较高的解向量则会引导算法较快地收敛,若收敛到局部最优,则很难再跳出局部最优解。因此,提高算法跳出局部最优的能力受到了研究者广泛的关注[6-13]。
文献[9-10]探索了和声记忆库考虑概率HMCR、基音调整概率PAR和基因调整步长bw的调节对算法的影响,提出动态参数策略提高算法性能。但算法中引入了过多的静态参数,导致算法的适用性降低。文献[11-15]分别研究了全局最好和声作为引导产生新和声的策略,提高算法全局收敛性能。其中,文献[11]在文献[9]的基础上研究了全局最好和声引导产生新和声的策略,虽然算法具有较好的全局收敛性,但算法的参数并未减少,而且新和声的分量从最好和声的随机一维引导产生,在解决实际工程问题时,容易破坏解向量的结构。文献[12]虽然提出新和声通过最好和声对应维的信息产生,但算法中仍然无法摆脱需要设置多个参数的困扰。文献[13]则将HMCR、PAR和bw三个参数排除,引入了位置更新和变异操作,虽然提高了算法的收敛性和跳出局部最优的能力,但算法又引入了新参数变异概率。最近,文献[15]在文献[13]的研究成果基础上,引入反向学习技术提高HS算法对解空间信息的开发能力,但算法的参数并未减少。上述研究成果虽然在一定程度上提高了算法的收敛精度和收敛速度,但仍然存在参数设置较多,收敛速度慢和陷入局部最优等问题。
本文提出随机交叉全局和声搜索(Random Crosser Global Harmony Search,RCGHS)算法。通过多策略学习随机交叉即兴创作产生新和声,结合反向学习策略提高算法全局搜索和局部搜索的能力,克服了算法易陷入局部最优的不足。
2 HS算法与反向学习
2.1 HS算法
HS算法通过和声记忆库考虑、随机选取和基因调整策略,对优化问题每个决策变量在一定范围内不断搜索和调整,从而获得最优解。主要包括参数与和声记忆库初始化、即兴创作、更新和判断终止条件5个步骤。其中,即兴创作可以描述为:

其中,rand表示0到1之间的随机数。表示新生成和声向量xnew的第 j维分量。xjL和xjU分别表示第 j维分量的下界和上界。
2.2 反向学习
反向学习[16]的原理是通过问题的可行解寻找其反向解并对二者评估,选出较优的解作为下一代个体。其中,反向点和反向学习优化的定义如下:
定义1反向点:假设x=(x1,x2,…,xD)为D维空间中的任意一点,且x1,x2,…,xD∈R,xi∈[ai,bi]。则与x对应的全局反向点定义为ox=(ox1,ox2,…,oxD),其中

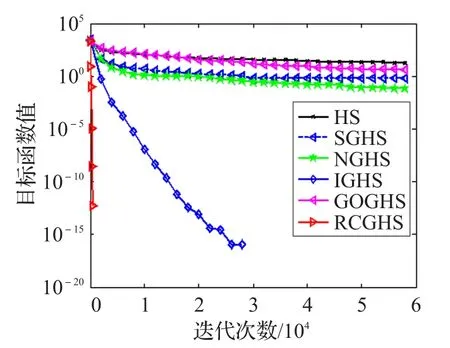
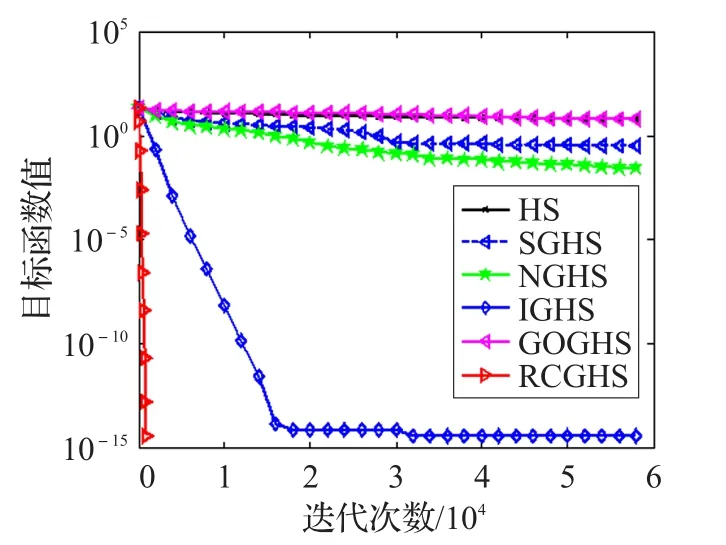
定义2反向学习优化:设x=(x1,x2,…,xD)为D维空间的一个点,其全局反向点ox=(ox1,ox2,…,oxD),考虑最小化问题,如果 f(ox) HS算法通过随机选择和声即兴创作策略,对小规模优化问题具有较好的优化效果。如果面临高维复杂优化问题,算法在进化后期的盲目搜索,会使和声记忆库的多样性变差,导致算法陷入局部最优难以跳出。相比之下,通过当前最好和声引导即兴创作,可以提高算法的全局收敛性能和算法的效率。文献[13]提出最差和声与最好和声的对称区间内产生新和声的策略。其中,新和声向量xnew的第 j维分量通过下面的策略产生,即 式(2)和(3)的实质可以看成是算法进化过程中,最差和声向最优和声学习的一种策略。 当前最差和声向最好和声学习,虽然可以使其快速向最好和声聚集,但很容易忽略其他一些有价值的和声附近的信息。尤其在解决多个局部最优值问题时,经过一定迭代次数之后和声集中于局部最优值附近,导致整个和声记忆库中的和声陷入一个狭小的空间内,从而使算法局部最优。 从经验学习的角度去考虑,如果只强调最差和声向最优和声学习,则忽略了其他和声与最优和声之间的经验交互。对于算法进化而言,算法局部搜索的能力则会随之降低。而最差和声代表了当前和声的适应度函数值是最差的,并不代表最差和声所有分量的信息都是最差且没有价值(潜力)的。对于最差和声向量来说,可能只有部分分量的信息是较差的。如果能将最差和声向量的某些分量借助其他和声对应分量的信息更新,则会提高算法的进化效率。此时,如果能够加强其他和声的某些分量向最优和声学习进行经验交互,从而实现对局部信息的搜索就显得尤为重要。 因此,通过随机选择其他和声与当前最优和声交互随机学习,增加其他和声与最优和声之间彼此交互的机会,既可以提高算法局部搜索的能力,也为和声记忆库即兴创作提供更有价值的信息,为产生高质量的和声提供有力的保障。 通过前面的分析,本文采用两种学习策略随机交叉的学习方式产生新和声。将和声记忆库中最差和声以及其他和声分别向最优和声学习的随机交叉动态产生新和声。同时,结合随机交叉反向学习策略扩大算法的搜索区域,提高算法搜索性能。 3.2.1 最差和声向最优和声随机学习 最差和声向最优和声学习动态产生新和声向量xnew的第 j( j=1,2,…,N )维分量,即 其中和分别表示最优和声与最差和声向量的第 j维分量。 通过最差和声在最优和声附近的对称区间内随机学习,可以有效开发最优和声解空间附近的信息。尤其在优化早期,不同和声之间的差异较大。通过最优和声引导创作新和声时,使当前最差和声对最优和声的学习可以快速向最优和声聚集,提高和声搜索算法的全局搜索性能。 3.2.2 其他和声向最优和声随机学习 为了增加其他和声与最优和声之间彼此交互,实现对其他和声附近解空间信息有效开发,提高算法局部搜索性能。在和声记忆库即兴创作过程中,新和声向量某一维以一定的概率随机选择一个和声xr与xbest对应的分量相互学习开发解空间信息,从而产生新和声向量xnew的第 j维分量,即 其中,r∈{1 ,2,…,HMS} ,和分别表示xr和xbest的第j(j =1,2,…,N )维分量。通过其他和声向最优和声随机交互学习进化,可以实现对其他和声附近解空间局部信息有效开发并利用,提高算法局部搜索的性能。不仅提高了和声记忆库中和声向量的质量,同时为后续即兴创作产生新和声向量提供指导作用。 3.2.3 随机交叉 本文将两种学习策略随机交叉即兴创作。新和声向量xnew的第j(j =1,2,…,N )维分量按照下面的规则执行。其伪代码为: If rand 执行式(4) Else 执行式(5) End if 两种学习策略随机交叉使新和声的一部分分量通过最差和声向最优和声学习产生,实现全局搜索。同时,新和声的另一部分分量通过其他和声向最优和声学习进行经验交互后产生,实现对局部信息的搜索。将二者随机交叉,发挥启发式优化算法的随机性的特点,通过其在全局搜索与局部搜索之间随机跳跃,避免了算法单一进行全局搜索或局部搜索的缺陷,从而实现全局搜索和局部搜索的动态平衡。此外,通过两种不同学习策略随机交叉动态产生新和声的策略,既保持了当前最优和声向量的特性,同时又继承了最差和声向量与其他和声向量的某些特质。随机交叉策略避免了最差和声向量某些分量信息对算法即兴创作的干扰,加快了算法的收敛速度,提高了算法的优化效率。 3.2.4 随机交叉反向学习 为了扩大算法的搜索区域,采用一种随机反向学习策略。其原理是:一方面通过两种学习策略产生的新和声向量xnew后,即兴产生其对应的反向和声向量oxnew;另一方面通过和声记忆库中最好和声xbest反向数的邻域值,通过每一维的迭代反向学习,产生反向和声向量oxnew。oxnew对应的第 j维分量按照下面的规则执行,即 通过反向解的引入,对新和声向量进行反向区域的搜索,可以扩大算法的搜索区域,增强算法的邻域搜索和全局搜索能力。 算法更新过程中,和声记忆库即兴创作产生的和声向量xnew与反向和声向量oxnew中适应度较优的个体直接替换和声记忆库中的最差和声。 RCGHS算法的操作步骤如下。 步骤1初始化优化问题和算法的参数: 设置和声记忆库大小HMS和最大迭代次数K。 步骤2初始化和声记忆库: 确定第 j个分量的范围[xjL,xjU],随机产生HMS个和声向量存入和声库中。 步骤3即兴创作产生新和声: For j=1 to N%即兴创作过程开始 If rand 执行式(4) Else 执行式(5) End if 执行式(6) End for 步骤4更新和声记忆库: xnew与oxnew适应度较优的个体直接替换和声记忆库中的最差和声向量。 步骤5判断终止准则: 如果当前迭代次数等于最大迭代次数K,则终止运行算法,否则重复执行步骤3和步骤4。 本文RCGHS算法通过两种不同学习策略随机交叉动态产生新和声。其中,第一种学习策略采用当前最差和声向当前最优和声学习进化,可以使当前最差和声快速向最优和声聚集,使新产生的和声成为最优和声的可能性大大提高,提高了算法的全局搜索性能。第二种学习策略,通过其他和声向量向最优和声学习,可以有效地对其他和声附近局部信息的开发,避免较差分量对新和声的干扰,提高算法局部搜索的性能。将两种学习策略随机交叉,使新和声在解空间不同区域内随机更新,可以实现算法全局搜索和局部搜索之间的平衡,提高了算法跳出局部最优的能力,使算法向全局最优收敛。 两种学习策略中通过当前和声记忆库中最优和声向量作为引导,使最差和声与其他和声均向最优和声向量学习实现解空间信息的开发。动态产生的新和声继承了和声之间交互学习后的经验,而且受最优和声的引导启发,保证新和声以一种单调递增的方式去产生,其实质是一种贪婪的选择策略使新和声逐渐向全局最优逼近,可以保证算法的收敛性。 在即兴创作后期利用反向学习技术搜索反向解空间,最终将二者适应度值较优的和声向量存储于和声记忆库中,其本质仍然是一种贪婪的选择策略。因此通过两种学习策略即兴创作动态产生的新和声,再结合反向学习策略创作新和声可以保证算法的收敛性。 将 RCGHS与 HS 算法[1]、SGHS算法[12]、NGHS 算法[13]、IGHS 算 法[14]、GOHS 算法[15]、人工 蜂 群 ABC 算法[4]、基本粒子群PSO算法[5]和灰狼GWO算法[6]进行优化性能测试。实验中选取优化算法6个经典标准测试函数,其中函数 f1~f3是单峰函数,函数 f4~f6是多峰函数,具体表达如下: f1:Sphere单峰函数 其中,-100≤xi≤100,全局最优为0。 f2:Schwefel’s problem 2.2.2单峰函数 其中,-100≤xi≤100,全局最优为0。 f3:Rotated hyper-ellipsoid单峰函数 其中,-100≤xi≤100,全局最优为0。 f4:Rastrigin多峰函数 其中,-100≤xi≤100,全局最优为0。 f5:Griewank多峰函数 其中,-100≤xi≤100,全局最优为0。 f6:Ackley多峰函数 其中,-100≤xi≤100,全局最优为0。 在仿真实验中取HMS=5,每种HS算法用到的参数选择参考文献中最优设置。ABC算法种群大小取30,limit=50;PSO算法,学习因子C1和 C2均取2,种群大小取30;GWO算法,种群大小取30。 实验中所有HS算法迭代60 000次,ABC、PSO和GWO算法分别迭代2 000次。实验中向量空间分别取N=50和N=100,每种算法独立运行30次,分别用Best代表最优值,Worst代表最差值,Mean代表平均值,Std代表方差,对6个函数的测试结果如表1和表2所示。 由表1和表2中对6个测试函数的优化结果来看,HS、SGHS、NGHS、ABC和PSO算法的优化效果相对较差,尤其是到了高维空间中,这几种算法均陷入了局部最优。IGHS、GOGHS和GWO算法的优化精度则相对有所提高。相比之下,无论在低维空间还是高维空间,本文RCGHS算法的优化效果明显优于其他几种算法的优化结果。RCGHS算法对6个函数优化均可以搜索到最优解,而且除了函数 f6外,对其他几个函数优化无论在低维空间还是高维空间中所得到的最差值和平均值均与最优解相同。由表1和表2的实验结果总体来看,本文RCGHS算法在高维空间中优化精度变化相对较小,其他几种算法的优化精度均有不同程度的下降。这说明RCGHS算法比其他几种算法更加稳定。 在实验中,函数 f4、f5和 f6均是多峰函数,RCGHS算法在低维空间和高维空间均可以搜索到其最优解,而且对 f4和 f5优化的最差值和均值都与最优解相同。尤其对多峰函数 f6优化很多算法都陷入了局部最优,而本文算法仍然可以搜索到最优解。这说明在解决具有多个极值问题时,RCGHS算法在当前最好和声引导即兴创作具有很强的全局搜索能力的前提下,增加其他向量向最优和声向量学习的策略后,算法加强了对其他和声附近信息的精细搜索,使算法的局部搜索能力得到了提高。此外,在算法进化后期,随机交叉策略结合反向学习技术实现对反向解得搜索,使算法能迅速摆脱局部最优的困扰,提高了算法跳出局部最优的能力。 表1 标准函数测试结果(N=50) 表2 标准函数测试结果(N=100) 图1 函数 f1最优值进化曲线 图2 函数 f2最优值进化曲线 图3 函数 f3最优值进化曲线 图4 函数 f4最优值进化曲线 图5 函数 f5最优值进化曲线 图6 函数 f6最优值进化曲线 为了对比几种和声搜索算法的收敛精度和收敛速度,本文给出了几种和声搜索算法对函数 f1~f6在高维空间(N=100)优化,每种算法迭代60 000次时的最优值进化曲线,如图1~6所示。 由图1~6中6个函数的最优值进化曲线可以看出,不论是从收敛速度还是收敛精度来看,RCGHS算法的优化效果明显优于其他几种HS算法。 根据表1和表2中的实验结果以及图1~6函数的最优值进化曲线总体上说,引入新的学习策略后,RCGHS算法对于6个标准函数优化的寻优精度得到了明显的提升,而且本文RCGHS算法的收敛速度明显快于其他几种改进HS算法。 在上面的仿真实验中,几种和声搜索算法除了和声记忆库大小HMS和迭代次数K两个参数外,每种算法的其他主要参数个数分别为:HS算法3个参数(HMCR、PAR 和 bw),SGHS算法5个参数 (HMCRm、PARm、bwmin、bwmax和 LP),NGHS算法1个参数 (Pm),IGHS算法2个参数(HMCR和PAR),GOGHS算法1个参数(Pm),RCGHS算法0个参数。根据算法的主观参数分析可以看出本文算法的主观参数最少,所以本文算法的实验结果受经验影响相对较小。 本文针对和声搜索算法容易陷入局部最优的问题,提出了随机交叉全局和声搜索(RCGHS)算法。通过不同的学习策略的随机交叉对解空间信息进行开发,并结合随机反向学习策略实现算法全局搜索和局部搜索的平衡。与其他HS算相比,RCGHS算法的主观经验参数设置较少,算法更具有适用性。利用优化算法6个标准测试函数对RCGHS算法与目前已发表文献中优秀的改进HS算法及ABC、PSO和GWO算法进行寻优效果比较,仿真结果表明RCGHS算法的寻优性能得到了有效的提升,验证了算法的有效性和稳定性。 [1]Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68. [2]谢宏,向启均,陈海滨,等.机器人逆运动学差分自适应混沌粒子群求解[J].计算机工程与应用,2017,53(8):126-131. [3]李艳娟,陈阿慧.基于禁忌搜索的人工蜂群算法[J].计算机工程与应用,2017,53(4):145-151. [4]Karaboga D.An idea based on honey bee swarm for numerical optimization,Technical Report-tr06[R].Erciyes University,Engineering Faculty,Computer Engineering Department,2005. [5]Kennedy J,Eberhart R C.Particle swarm optimization[C]//IEEE International Conference on Neural Networks,1995:1942-1948. [6]Mirjalili S,Mirjalili S M,Lewis A.Grey wolf optimizer[J].Advances in Engineering Software,2014,69:46-61. [7]Molina-Moreno F,García-Segura T,Martí J V,et al.Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms[J].Engineering Structures,2017,134:205-216. [8]Al-Betar M A,Awadallah M A,Khader A T,et al.Tournament-based harmony search algorithm for non-convex economic load dispatch problem[J].Applied Soft Computing,2016,47(C):449-459. [9]Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems[J].Applied mathematics and computation,2007,188(2):1567-1579. [10]Chen J,Pan Q,Li J.Harmony search algorithm with dynamic control parameters[J].Applied Mathematics and Computation,2012,219(2):592-604. [11]Omran M G H,Mahdavi M.Global-best harmony search[J].Applied Mathematics and Computation,2008,198(2):643-656. [12]Pan Q K,Suganthan P N,Tasgetiren M F,et al.A selfadaptive global best harmony search algorithm for continuous optimization problems[J].Applied Mathematics and Computation,2010,216(3):830-848. [13]Zou D,Gao L,Wu J,et al.Novel global harmony search algorithm for unconstrained problems[J].Neurocomputing,2010,73(16):3308-3318. [14]Valian E,Tavakoli S,Mohanna S.An intelligent globalharmony search approach to continuous optimizationproblems[J].Applied Mathematics and Computation,2014,232:670-684. [15]Guo Z,Wang S,Yue X,et al.Global harmony search with generalized opposition-based learning[J].Soft Computing,2017,21(8):2129-2137. [16]Tizhoosh H R.Opposition-based learning:A new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling,Control and Automation,and International Conference on Intelligent Agents,Web Technologies and Internet Commerce,2005,1:695-701.3 RCGHS算法
3.1 算法改进分析
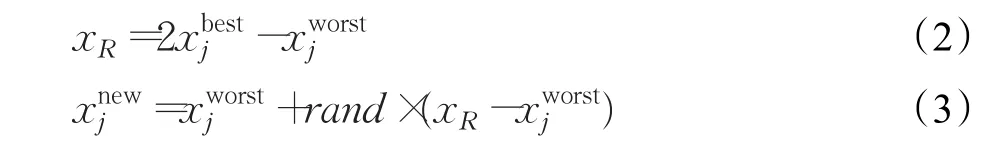
3.2 即兴创作
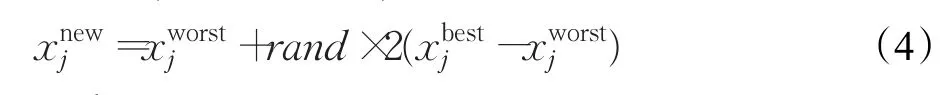
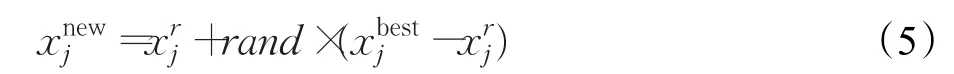
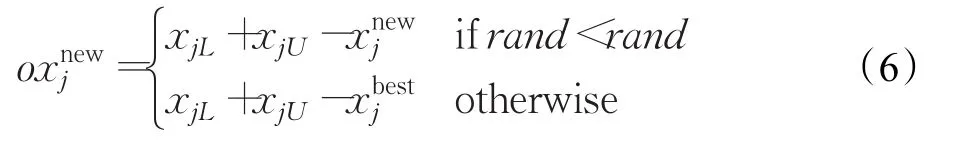
3.3 更新和声记忆库
3.4 算法操作步骤
3.5 收敛性分析
4 仿真实验
4.1 仿真实验准备
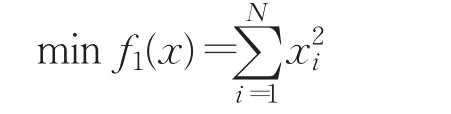
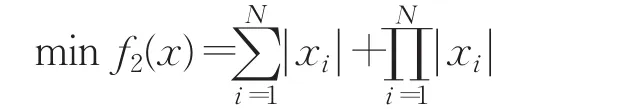
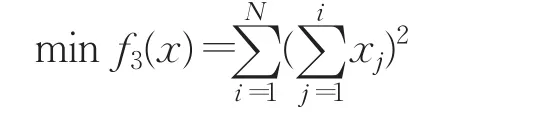
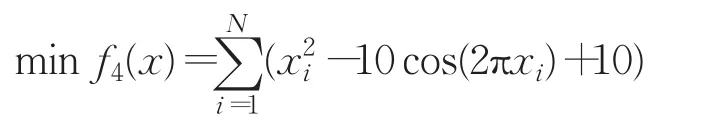
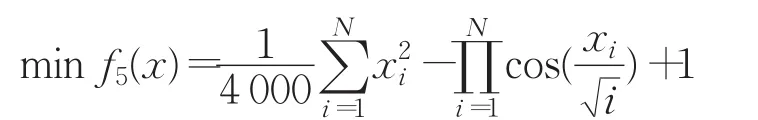
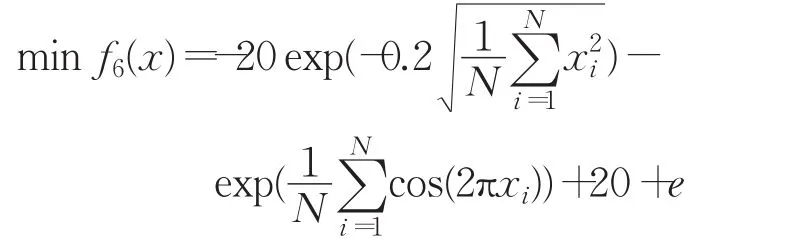
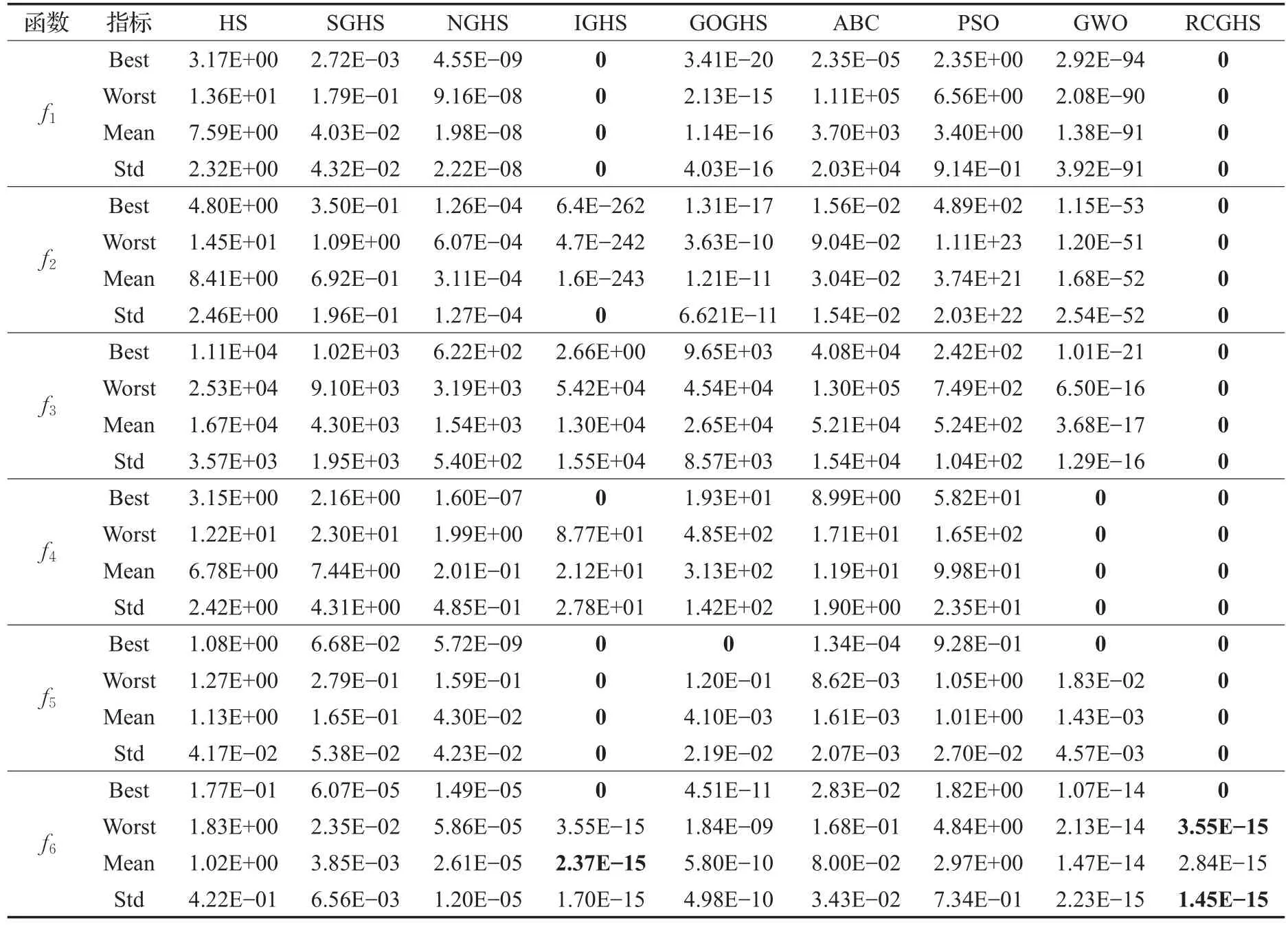
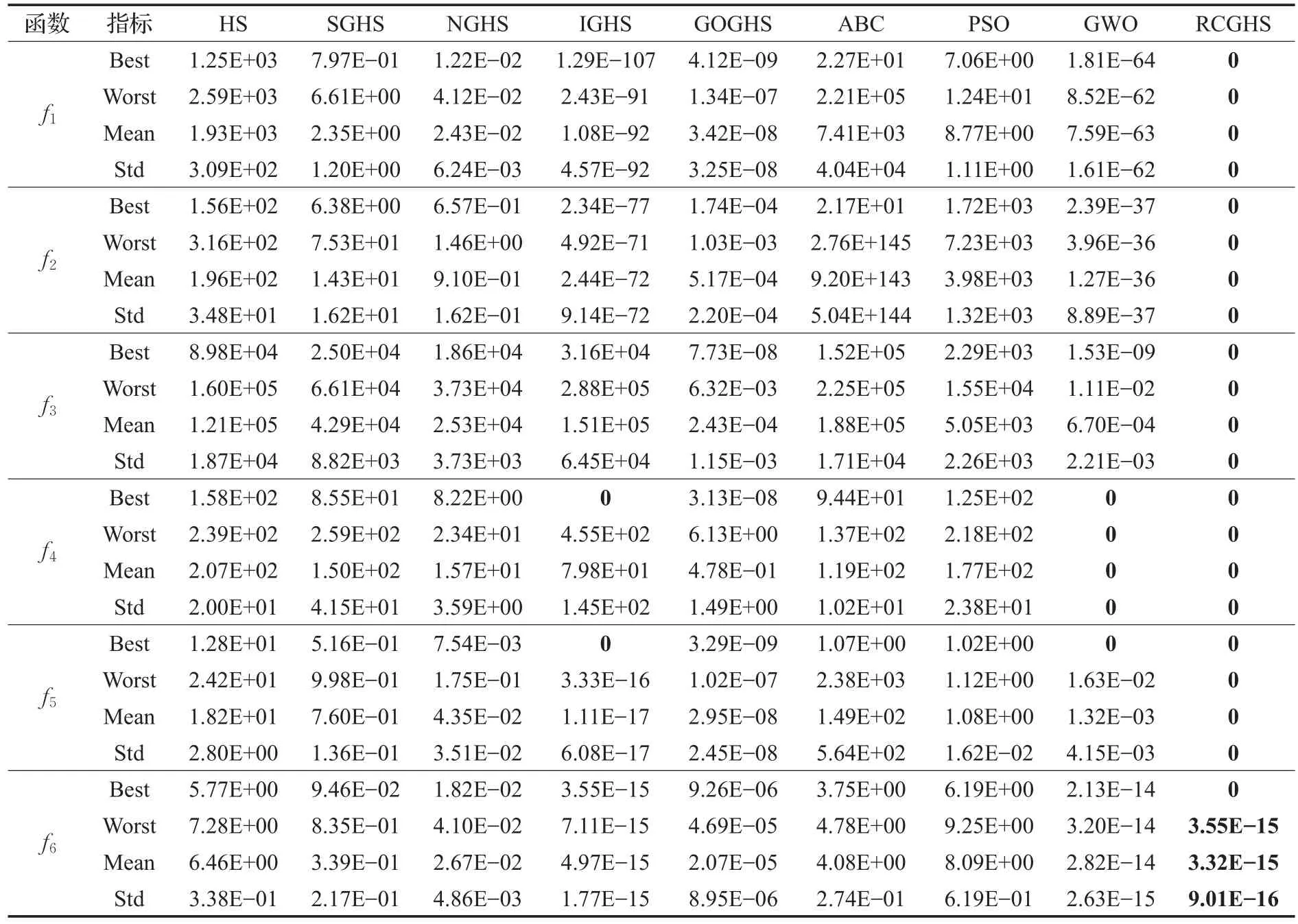
4.2 仿真结果与分析
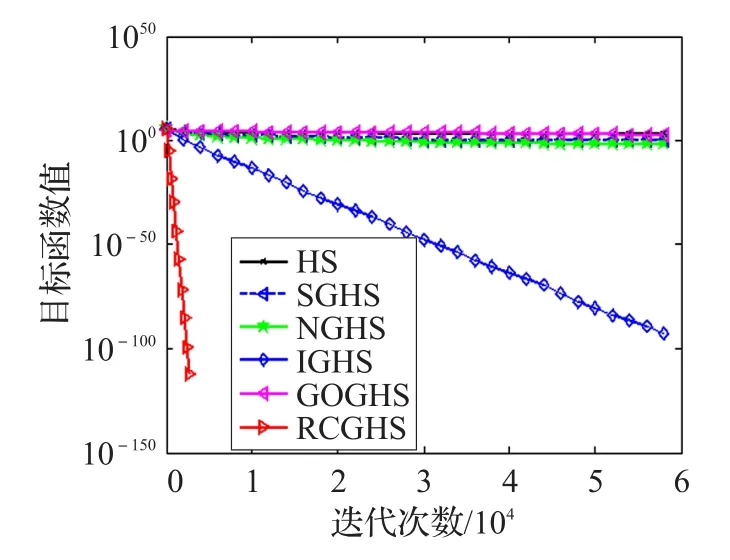
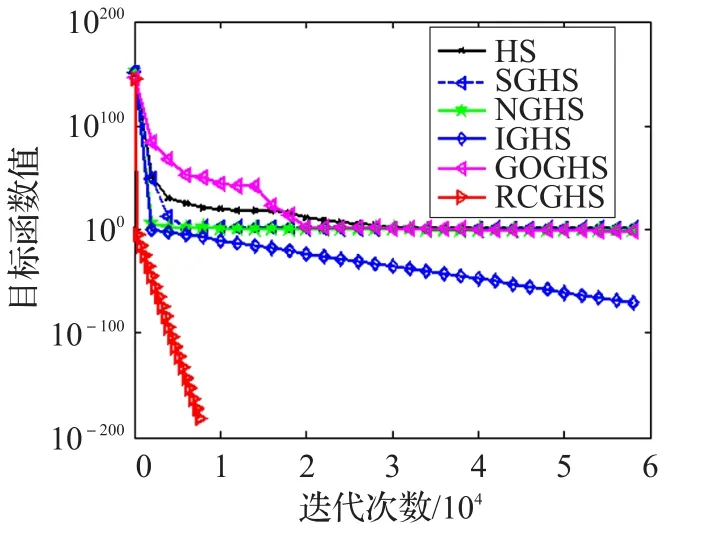
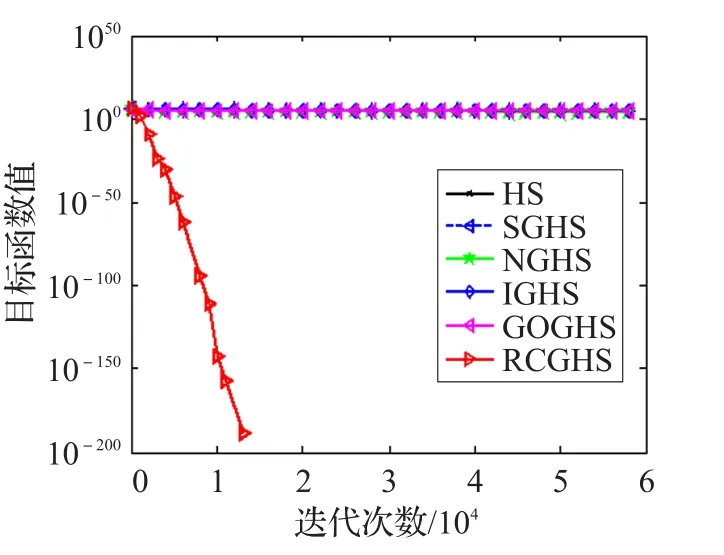
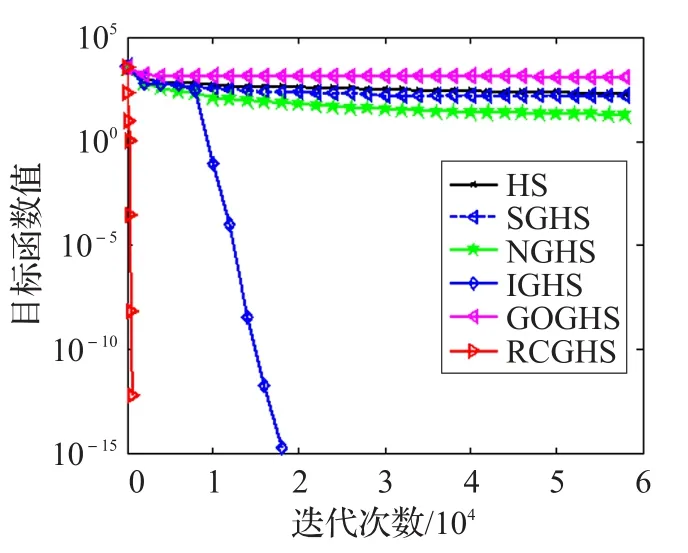
4.3 算法参数分析
5 结束语
