基于融合百度指数的电商订单量组合预测研究

王长琼，曹乜蜻，王艳丽，邱 杰，刘晓宇

武汉理工大学 物流工程学院，武汉 430063

1 引言

近年来，随着中国电子商务爆发式的增长，用户需求预测成为企业电子商务战略的核心部分，并对市场导向与库存控制具有积极影响。

在电商需求分析方面，李长春对阿里电商平台的交易数据进行挖掘，并运用随机森林方法对商品需求进行动态预测[1]。许圣佳、蒋炜通过利用点击量和购买量的历史信息进行需求预测，运用阿里巴巴大数据进行实证分析[2]。Qiu等人在电商环境下建立客户购买预测模型（COREL），并运用京东数据调查客户动机，挖掘顾客消费偏好[3]。Yang等人通过网站进行市场购物篮分析以挖掘消费者网上购物模式[4]。综上可知，学者们已经对电商环境下的需求变化进行了探究，但是单一的预测模型本身的局限性会影响预测精度，同时网购用户订单需求预测的相关研究相对缺乏。

在网络搜索应用方面，孙烨等人通过加入百度指数的VAR模型对三清山日游客量进行预测分析，发现移动端百度指数比PC端有更好的预测效果[5]。张爱华等人以余额宝资产规模为例，运用ARIMA模型构建引入互联网搜索量的市场需求预测模型[6]。Preis通过分析谷歌中与金融相关的搜索词的变化，发现该模式可以成为股票市场波动的“预警信号”[7]。Hand等人研究发现谷歌趋势数据可以提高电影录取预测模型的准确性[8]。综上所述，网络搜索产生的影响日益增大，但目前在网络搜索对电商用户订单预测方面的研究尚未明确。

在组合预测模型方面，王宁等人在训练过程中采用网格搜索法对支持向量机回归模型参数进行优化[9]。丁宏飞等人通过蜂群优化算法对参数进行优化，提出了一种基于多模型融合预测算法的BP神经网络和支持向量机相结合的组合预测方法[10]。丁闪闪等人采用Adaboost算法对BP神经网络进行优化，构建了BP_Adaboost预测模型，以改善传统BP神经网络的预测性能并利用南京市典型道路数据对该方法进行了性能评价[11]。杨波、吴涵等人建立趋势曲线预测模型、回归预测模型及灰色预测模型的物流需求单项预测模型，以Shapley值为权重确定方法，建立了组合预测模型，并以重庆空港物流园为例进行应用[12]。Tselentis等人比较了统计与贝叶斯组合模型和经典单时间序列模型在短期交通预测中的表现，并证明了组合预测的风险比选择单一模型的风险要低[13]。Voronin等人结合小波变换、ARIMA模型和神经网络，建立组合预测模型，同时对电力需求和价格进行预测[14]。李翔、朱全银针对传统BP神经网络容易陷入局部极小、预测精度低的问题，提出使用Adaboost算法和BP神经网络相结合的方法，提高网络预测精度和泛化能力[15]。综上所述，组合预测模型在一定程度上可以有效地提高预测精度，但在电商应用方面还较少，选取的数据和指标较为单一。

本文拟建立基于BP神经网络、基于Adaboost的BP神经网络、支持向量机SVM（Support Vector Machine）的组合预测模型，以避免单一模型的不足。同时，本文将影响网购用户的直接因素与相关网络指数结合，构建一套融合百度指数和电商订单衍生信息的指标体系，以进一步提高组合预测模型精度。

2 组合预测模型原理

2.1 组合预测模型

组合预测能够整合单项预测的优势，较大限度地利用各单项预测样本信息，有效弥补单一预测因随机因素的影响导致预测误差较大的缺点，从而提高整体预测精度。针对BP神经网络易陷入局部最优化、Adaboost算法对异常样本的敏感、SVM对大规模训练样本的困难性，本文将适用于物流需求预测的BP神经网络预测方法、基于Adaboost的BP神经网络预测方法、支持向量机SVM预测方法三种方法的预测结果进行结合，选择Shapley组合预测法对结果进行处理，得出更为满意的预测方案。

步骤1根据网购订单量影响因素构建融合百度指数的订单量预测指标体系，区分训练数据与预测数据，并对原始数据进行归一化等预处理。

步骤2通过BP神经网络模型、支持向量机SVM模型对预处理的数据进行预测分析，得出预测数据。同时，将相同结构的BP神经网络使用Adaboost算法进行优化，构建基于Adaboost的BP神经网络模型，得到其预测数据。

步骤3计算各模型训练数据的平均相对偏差MRD（Mean Relative Deviation）：

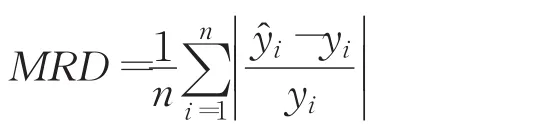
其中，yi为训练原值，为训练所得预测值，n为训练组数。

步骤4根据各模型平均训练MRD，计算各模型Shapley值的分配，并确定组合预测中各预测方法的权重。

步骤5根据各模型分配的权重计算预测数据的组合预测结果。

组合预测算法原理如图1所示。

图1 组合预测模型原理图

2.2 算法详细设计

目前，在物流需求预测神经网络方法中主要是采用BP网络，但在进行学习训练时BP神经网络随机初始化权值与阈值往往会降低其收敛速度，容易陷入局部极值问题。BP神经网络模型最重要的是输入层、隐含层、输出层神经元个数的选择以及激励函数、训练函数的确定，这需要通过大量实验来选择。

Adaboost算法是Boosting算法的一种改进算法，能对弱预测器的误差进行适应性调整，从而达到提高任意弱预测器的预测精度的目的。但Adaboost算法对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。本文以BP神经网络作为集成模型的弱预测器，利用Adaboost算法的思想集成BP神经网络，使用加权后选取的训练数据代替随机选取的训练样本，将弱分类器联合起来，得到BPAdaboost强预测器。构建的BP-Adaboost强预测器是由多个BP网络组成，能有效克服单一BP神经网络的缺点。计算流程及模型结构见图2。

图2 基于Adaboost的BP神经网络模型结构

支持向量机SVM可用于回归预测分析，对订单量或快递量进行有效预测。SVM能够较好地解决小样本、非线性、高维数问题，常被用于识别和预测。但SVM算法对大规模训练样本难以实施。其重点在于：第一，回归函数的确定。本文采用极小化优化模型来确定回归函数。第二，核函数的确定。核函数的选择决定了特征空间的结构。本文采用基于径向基RBF（Radial Basis Function）核函数，该函数能够很好地实现非线性映射。

Shapley值法是确定各单项预测方法在组合预测方法中的权数的大小，N种单项预测方法根据各自误差的大小来分配权重。Shapley值实现的是每个合作成员对该合作联盟的贡献大小，突出反映了各个成员在合作中的重要性。其最大优点就是原理和结果易于被各个合作方视为公平，结果易于被各方接受。

算法步骤如下：

（1）选取指标，并运用不同单预测模型对因变量进行预测，得到预测值。

（2）计算组合预测中各单预测方法的权重。Shapley值的分配公式为：

其中，n为预测方法数目，s为集合I={1,2,…,n}中的任意子集，Ei为该预测模型分得的误差量（即Shapley值），E(s)为各组合的误差，w(||s)为加权因子。根据上述计算结果确定组合预测中各预测方法的权重，公式为：

其中，E为组合预测的总误差。

（3）计算组合预测结果。在t时刻的组合预测值可表示为：

其中，Yit表示第i种预测方法在t时刻的预测值。

2.3 SVM的信息粒化时序回归预测

如果能知道电商订单量或快递量的变化趋势和变化空间，这对于企业来说是非常有帮助的。本文利用SVM对进行模糊信息粒化后的电商相关指数进行变化趋势和变化空间的预测，并选择W.Pedrycz模糊粒化方法模型进行数据处理。

对于给定的时间序列X(x1,x2,…,xN)，考虑单窗口问题，即把整个时序X看成是一个窗口进行模糊化。本文采用三角型模糊粒子，其隶属函数如下：

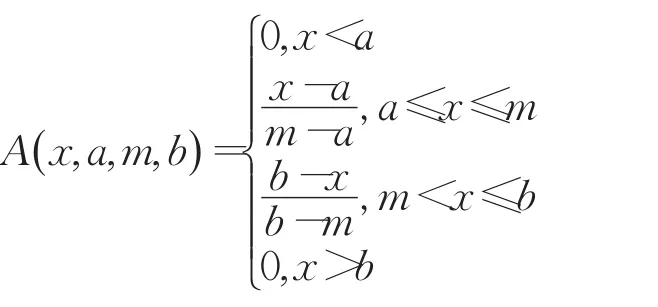
W.Pedrycz模糊粒化方法建立模糊粒子的基本思想为：（1）模糊粒子可以很好地代表原始数据；（2）模糊粒子要有一定特殊性。为了满足上述的两个要求，找到两者的最佳平衡，可考虑建立如下的关于A的一个函数：

其中，MA满足建立模糊粒子的基本思想（1）；NA满足建立模糊粒子的基本思想（2）。

W.Pedrycz将信息粒化理论用到时间序列分析中，对时间序列进行信息粒化，取得了很好的效果。故本文用W.Pedrycz模糊粒化方法对电商订单量时间序列进行模糊粒化，利用SVM对模糊粒化后的数据进行变化趋势和空间的回归预测。

3 基于融合百度指数和电商用户订单信息的指标模型

由于网购订单量受多重因素的影响，涉及到的行业和企业也是五花八门，不同行业和企业在电商预测方面所采用的指标也不尽相同。因此，通过分析影响因素来构建一个适用于网购订单量的综合评价指标体系，就具有十分重要的理论与现实意义。针对电商整体环境和市场运营方式，本文总结了以下两类影响因素：

（1）电商网购订单直接影响因素

①用户行为导向因素，即用户的行为对电商交易额和交易量的影响因素。从当前市场环境下的需求方来说，用户行为主要包括商品浏览、商品加入购物车、店铺收藏、用户登录次数等方面。

②商家行为导向因素，即商家为维持、促进店铺交易额从而获取利润的行为对市场的影响。从市场供应方来说，商家行为主要包括商品单价、商品折扣力度、同行业水平、用户评价展示和预售等方面。

③交易行为导向因素，即在供需双方交易的过程中产生的数据流对下笔交易所产生的影响。通常包括交易额、交易量、订单笔数、下单用户数、第三方支付方式等因素。

（2）网络搜索间接影响因素

搜索引擎所记录下的海量数据与电商用户的兴趣、需求、“用户关注度”甚至未来行为必然存在着关联。如果能够有效挖掘“搜索数据”中的用户需求信息并加以利用，这些影响因素对于电商交易订单需求预测精度的提高和市场趋势把握力度的增大会是很强助力。目前，将网络搜索数据作为影响因素来预测电商订单需求量的研究还较少，本文会结合百度指数关键词搜索对预测精度的影响展开研究。关键词的选取方法主要包括直接取词法、相关取词法、技术取词法等。考虑到数据的可获得性，本文会通过对基准关键词的直接搜索来建立影响因素指标体系。此外，由于移动端百度指数比PC端使用广泛、更具代表性，选择移动端指数可以使得预测结果更为精确。

本文通过对用户行为日志数据的处理，结合上述影响因素，通过SPSS软件对影响因素指标和评价因素指标之间进行相关性分析，选取通过显著性检验且相关系数大于0.85的指标作为最终指标，构建了基于融合百度指数和电商用户订单信息的指标体系，如表1所示。

表1 电商物流需求预测指标体系

4 实例分析

4.1 样本收集与预处理

本文选取了某一时间段内百度指数关键词搜索量和某电商平台68万条数据，以周为单位对这些数据进行分类整合，按照上文所构建的指标体系整理出了连续32周的数据，选取前31组数据训练，用第32组数据测试。如表2所示。在软件运用方面，针对各影响因素和评价指标之间相关关系的问题，采用SPSS软件进行检验；针对组合预测建模，采用Matlab软件进行求解。

表2 某区域电商订单需求预测指标统计数据

4.2 预测与结果分析

4.2.1 模型参数设置

根据指标体系，BP网络输入层神经元个数为7，输出层神经元个数为1，通过实验选取隐含层神经元个数为7。此外，根据实验对比分析，最终选取logsig函数作为激励函数，trainlm函数作为训练函数，训练次数200 000，训练目标100E-05。

在基于Adaboost的BP神经网络预测模型中，采用10个BP神经网络作为弱预测器组成的强预测器对订单量进行预测，把弱预测器预测误差超过0.1的测试样本作为应该加强学习的样本。BP神经网络的参数设置与上文相同。

在SVM预测模型中，使用matlab中libsvm工具箱进行SVM回归，默认径向基函数（RBF）作为SVM的核函数，通过matlab编程、采用交叉验证方法实现对回归最佳惩罚参数c和核函数参数g的寻找。

4.2.2 结果分析

单项预测方法的预测结果和平均相对偏差MRD如表3所示。可以看出，BP神经网络对这组数据适应度较好，基于Adaboost的BP神经网络和SVM的训练拟合程度相对较差，但从后文的第32组数据看，其预测能力均高于BP神经网络。

计算各成员Shapley值，再根据权重计算公式调整权重，故最终组合预测模型为：

Y=0.640Y1+0.185Y2+0.175Y3

利用组合模型对第32组数据进行预测，预测结果如表4所示。

（1）组合预测结果分析

结合表3、表4，可以看出，组合预测模型的预测误差可以收敛到1.25%，达到很好的预测效果。而预测误差最低值所使用的SVM模型，其训练误差却高达5.47%；与此相反，在训练过程中表现突出的BP神经网络模型，预测时的误差却是最大值2.95%。Shapley值组合预测的预测值会比较平稳，不像其他单一模型的预测值波动较大，这也是组合预测模型的一大优势。而且Shapley值法科学合理的分配各单一模型权重，使其误差也会与精度最优的模型相差不大。组合预测模型还具有现实可操作性和较强的实用性。

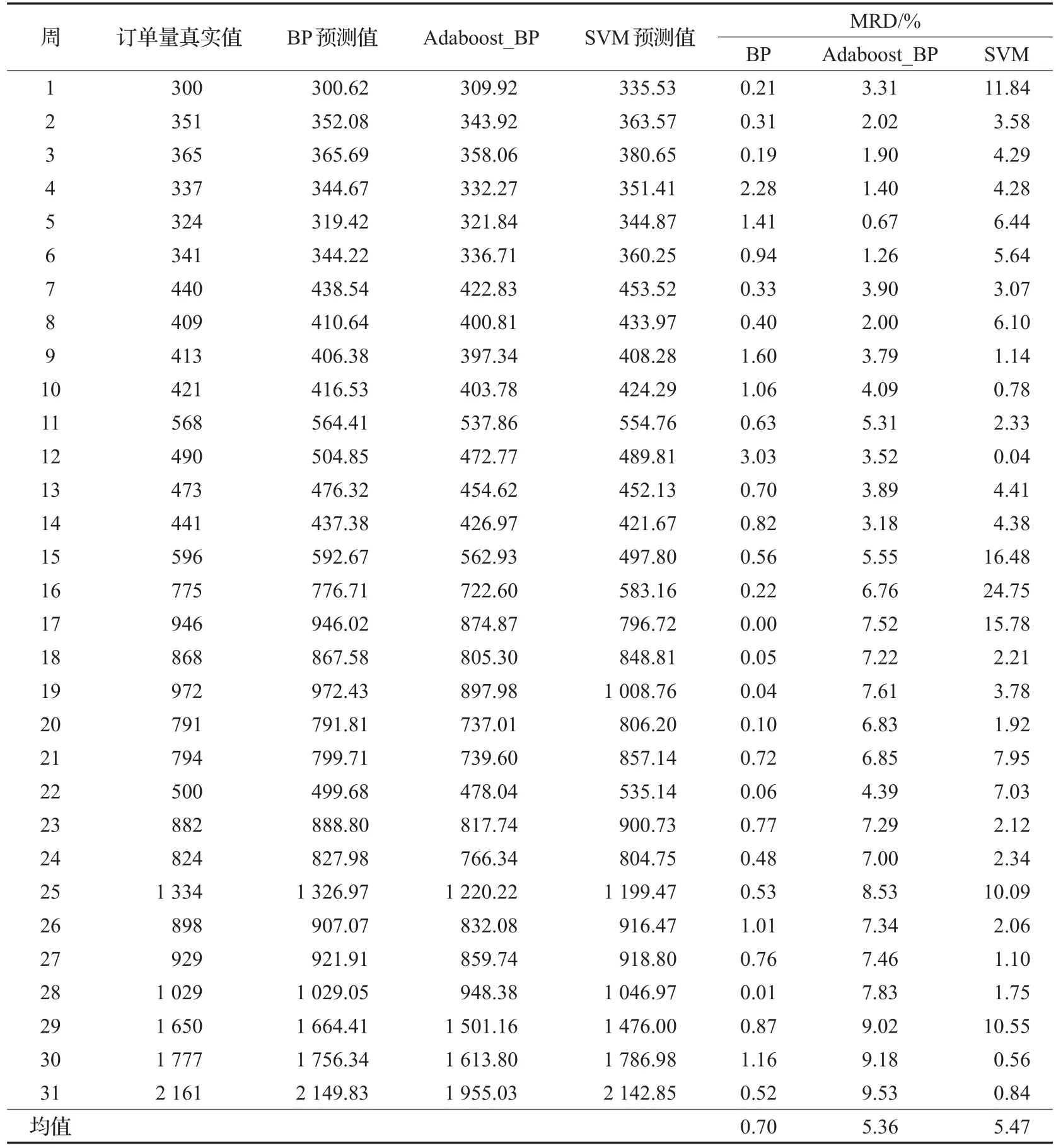
表3 各单预测模型训练结果和训练相对误差

表4 组合预测结果

（2）误差MRD波动分析

各模型MRD波动情况如图3所示。

图3 平均相对偏差MRD波动图（融合百度指数）

SVM模型和基于Adaboost的BP神经网络模型在前31组的训练中表现较差，但第32组的预测结果精度很高；BP神经网络的前期训练结果非常好，但在预测过程中误差猛增，且由于神经网络本身随机性较强，使得实验结果并不稳定，在实验过程中甚至出现误差非常大的个别情况。Shapley值组合预测模型的预测结果相对稳定，始终保持在5%以内，即使在SVM模型出现较大失误的情况下也可以快速修正，且最终的预测误差非常低。

（3）预测值与原始值的拟合程度分析

Shapley值组合预测值与原始值的拟合图如图4所示。可以看出组合模型的预测值与数据原始值的拟合程度非常高，可以有效地对电商订单量的波动做出正确的判断和预测。

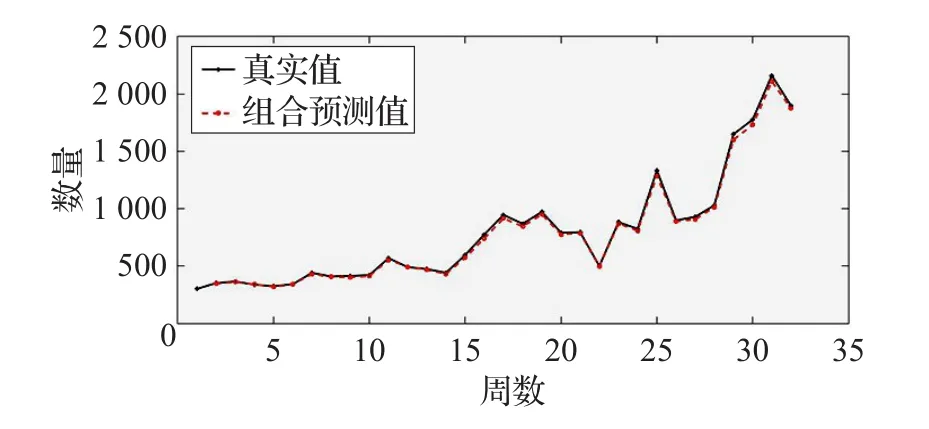
图4 拟合趋势图

本文用可决系数R2来衡量预测值与原始值的拟合程度。可决系数R2越大，说明模型对原始值的拟合程度越好。拟合数据结果如表5所示。

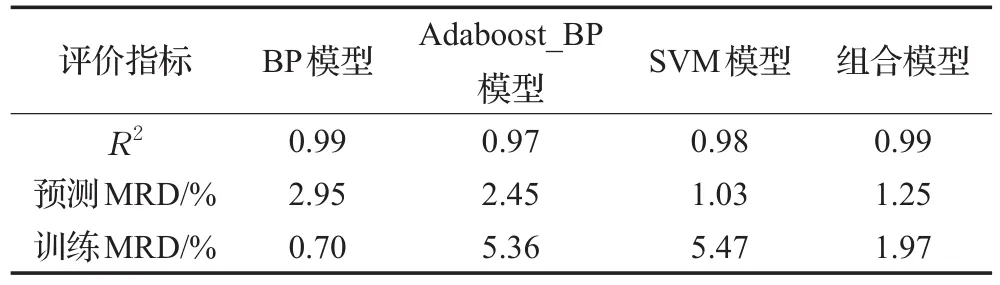
表5 拟合数据结果

从可决系数R2反映的数据来看，组合模型的预测值与原始值的拟合程度在4种模型中排名第一，高达99%，说明各样本预测点与回归线靠得非常近，由样本回归做出解释的离差平方和与总离差平方和十分相近，也就是拟合优度非常高。这就证明了本文所提出的组合预测模型对于电商订单量预测的适应性和准确性。同时，将每个指标中准确度排名靠前的两组数据在表中标出，可以直观清楚地看到，本文所提出的组合预测模型在三项指标中全部表现出色。相对于单项预测模型的单项预测评价指标，组合预测模型的预测精度有所降低，但组合预测模型仍然可以较好地刻画电商订单量的整体变化趋势，预测结果可以为电商管理人员提供有价值的参考信息。

在电商订单量不断变化的今天，组合预测模型可以更好地适应不断变化的数据，避免单一模型对数据不适应性而导致的预测失真。

4.2.3 百度指数比较分析

为了研究加入了百度指数作为预测指标后模型的有效性，本文另做了一组6个输入指标（不包括百度指数）的实验，与上述实验对比分析，实验结果如图5所示。

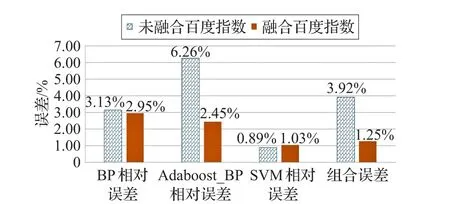
图5 预测误差对比分析图

从实验结果可以看出，6个指标输入的实验误差相对较大，融合了百度指数作为预测指标的实验，尤其是对于基于Adaboost的BP神经网络模型、本文所构建的组合预测模型来说，预测结果更为精确。该研究证明了网络搜索关键词对电子商务订单量预测的起着明显的影响作用，可以作为反映电商订单量预测趋势的影响因素。

4.3 趋势预测

趋势结果如图6、图7所示。Low=2 076.77,r=2 595.56,Up=2 595.56，即，在接下来的两周中，订单量的变化趋势和变化空间为[2 076.77,2 595.56]。这个结果可对物流公司或供应链企业车辆调配、提前调货等方面提供有力依据。

图6 Low趋势拟合图

图7 Up趋势拟合图

5 结束语

本文对电商环境下的用户订单量预测进行研究。实验证明，组合预测模型比BP神经网络模型、基于Adaboost的BP神经网络模型、支持向量机SVM模型更能适应动态变化的数据，训练和预测过程中都能保持较小稳定偏差波动，准确度达到98.75%。同时，本文构建了基于融合百度指数和电商用户订单信息的指标体系模型，将百度指数关键词“快递”的移动端搜索数据量融入电商订单量变化的影响因素。通过对比试验，融合百度指数的组合预测模型准确度比未融合模型高2.67%，证明了百度指数作为网购订单量预测影响因素的有效性，为电商企业预测用户需求提供了一种新思路。

[1]李长春.大数据背景下的商品需求预测与分仓规划[J].数学的实践与认识，2017，47（7）：70-79.

[2]许圣佳，蒋炜.电子商务环境下基于点击流的需求预测模型和企业库存优化[J].上海管理科学，2016，38（2）：18-27.

[3]Qiu Jiangtao，Lin Zhangxi，Li Yinghong.Predicting customer purchase behavior in the e-commerce context[J].Electronic Commerce Research，2015，15（4）：427-452.

[4]Yang Yinghui，Liu Hongyan，Cai Yuanjue.Discovery of online shopping patterns across websites[J].Informs Journal on Computing，2013，25（1）：161-176.

[5]孙烨，张宏磊，刘培学，等.基于旅游者网络关注度的旅游景区日游客量预测研究——以不同客户端百度指数为例[J].人文地理，2017（3）：152-160.

[6]张爱华，韩怡嘉.基于互联网搜索信息的预测模型研究——以余额宝产品需求为例[J].北京邮电大学学报：社会科学版，2015，17（3）：36-41.

[7]Preis T，Moat H S，Stanley H E.Quantifying trading behavior in financial markets using Google trends[J].Scientific Reports，2013，3：1684.

[8]Hand C，Judge G.Searching for the picture：Forecasting UK cinema admissions using Google trends data[J].Applied Economics Letters，2012，19（11）：1051-1055.

[9]王宁，谢敏，邓佳梁，等.基于支持向量机回归组合模型的中长期降温负荷预测[J].电力系统保护与控制，2016，44（3）：92-97.

[10]丁宏飞，李演洪，刘博，等.基于BP神经网络与SVM的快速路行程时间组合预测研究[J].计算机应用研究，2016，33（10）：2929-2932.

[11]丁闪闪，王维锋，季锦章，等.基于时空关联和BP_Adaboost的短时交通参数预测[J].公路交通科技，2016，33（5）：98-104.

[12]杨波，吴涵.基于组合预测模型的物流园区物流需求预测——以重庆空港物流园为例[J].数学的实践与认识，2015，45（20）：16-25.

[13]Tselentis D I，Vlahogianni E I，Karlaftis M G.Improving short-term traffic forecasts：To combine models or not to combine?[J].Intelligent Transport Systems Iet，2015，9（2）：193-201.

[14]Voronin S，Partanen J.Forecasting electricity price and demand using a hybrid approach based on wavelet transform，ARIMA and neural networks[J].International Journal of Energy Research，2014，38（5）：626-637.

[15]李翔，朱全银.Adaboost算法改进BP神经网络预测研究[J].计算机工程与科学，2013，35（8）：96-102.