基于截面数据的C1插值融合曲面重建

赵欢喜，初小宇

中南大学 信息科学与工程学院，长沙 410083

1 引言

基于截面数据的曲面重建是指根据已知的三维物体的若干截面上的数据点或者曲线数据，重新构建其立体数字化模型的过程。目前，曲面重建技术被大量应用到船体表面重建、工业产品样品制造以及CT切面模型重构等重要领域中，一个还原精确、数据冗余量小的重建模型对实现设计目标至关重要。

在曲面重建过程中，基于截面数据进行拟合并重建曲面是经常遇到的问题，这类数据由一组有序的截面轮廓线组成，每条截面线上有若干个有序排列的三维数据点。对于这类问题，目前常用的方法步骤如下：（1）分别对每行截面数据点进行拟合，构成一组有序的截面曲线；（2）对这组截面线通过蒙皮、拉伸等方法构造待建曲面。NURBS曲面由于其优秀的几何性质和在自由曲面造型和规则曲面造型中良好的表现力，目前被大量应用于曲面重建中；然而NURBS方法进行曲面重建面临着如何获取一组节点矢量相同的截面曲线的问题。这个问题可以通过直接的节点插入解决，但这使控制顶点反求的计算过程变得非常复杂，最后重建的曲面上将产生大量的控制顶点，造成了数据量膨胀，并且随着截面数目的增加，该问题变得更加显著。

针对这个问题，国内外学者对于如何在不牺牲曲面精度的条件下减少截面线上的控制顶点数，做了大量的研究[1-12]。文献[1]将其转化为带约束的能量最小化问题，使用法向量的梯度作为能量值，用水平集函数表示曲面，通过求该问题的解来得到曲面；文献[2]提出一种基于预制模板的曲面重建方法，通过放缩和变换进行原始轮廓与模板之间的匹配，随后通过重新参数化来得到控制顶点；文献[3]中Piegl和Tiller通过直接寻找一条理想的节点矢量来减少控制顶点的数量，该方法在减少数据冗余上效果显著，但得到的曲面形状是否精确非常依赖于节点矢量的设置是否理想；文献[4]中Liu等引入了细分方法来改善截面上数据点大量增加的问题；文献[5]中，Shamsuddin在上文的基础上提出了一种改良的向心参数化方法，先寻找控制顶点数最多的截面线，在误差容忍的范围内来减少曲线上的控制顶点数，用求得的节点矢量调整剩余的截面线，达到减少控制顶点数的目的；文献[6]中，曲学军等基于统计的方法对数据点的分布规律进行了分析，从而确定初始节点向量，合理地控制了生成的曲面上的控制顶点数目；文献[7-8]提出一种可调节区间的方法来调整控制顶点，在弹性区间内寻找尽量相近的节点并合并，能够有效地减少数据冗余，也能获得较为满意的参数化结果，但该方法受噪声的影响较大；文献[9-11]通过重采样重新取点，并进行重新参数化，从而求得一系列匹配点对，减少了节点矢量相容过程中的大量节点插入；文献[12]先构造低阶的插值曲线和曲面来拟合数据点，随后逐渐升阶来逼近待建曲面，避免了数据的参数化和节点向量选取不当造成的形状扭曲问题，但缺乏拟合复杂曲面的能力。以上方法都是通过构造合适的公共节点向量来实现曲线的相容性拟合，虽然相对之前的方法能够有效地减少控制顶点的数目，曲面得到了压缩，但是NURBS曲面需使用矩形网格的控制点这一缺点没有得到根本解决，这使得很多的控制点存在的意义只是为了满足拓扑上的限制，而并没有提供实际有意义的几何信息，最后构造出的曲面依然存在大量的冗余控制点。目前针对这种情况的研究较少，文献[13-16]采用T样条曲面来构造曲面，控制网格中可以存在T型的控制顶点，从而可以基于节点向量不同的截面线直接进行曲面拟合，有效地改善节点插入带来的数据量增大问题，同时保留了良好的局部控制能力，不过T样条曲面在进行网格化和处理曲面拼接上更加麻烦。

为了避免NURBS方法中构建曲面需要进行的节点矢量相容的过程，同时能够直接通过对原始数据插值来构造更精确的待建曲面，本文提出了一种双方向融合插值的C1参数曲面重建方法，利用融合的思想来构造截面曲线并处理曲面拼接，取得了较好的冗余量减少的效果。

2 融合曲面重建方法

本文提出的双方向融合插值的C1参数曲面重建方法共分两步，第一步插值截面上相邻的数据点构造曲线段，然后引入融合算法[17-18]将曲线段进行拼接，以得到光滑的截面轮廓曲线；第二步，插值相邻截面的轮廓曲线构建一系列曲面片，再次使用融合算法将所有曲面片进行拼接，从而得到一个光滑的待建曲面。该方法可以基于原始数据点数目不同的截面进行分段插值曲面重建，不会产生由于节点插入带来的大量的数据冗余以及复杂的计算过程；本方法同时采用了融合的思想来处理分段曲线、曲面的拼接，改良了传统参数曲线、曲面拼接方法需要边界条件的缺陷。

2.1 问题描述

给出一个物体的一组截面数据，表示为Ci,(i=1,2,…,n-1,n)，第i个截面Ci上的数据点表示为Pi,j,(i=1,2,…,n-1,n;j=1,2,…,mi)；根据这组截面数据插值构建截面曲线Fi(u),(i=1,2,…,n-1,n)，然后构建一个参数曲面S(u,v),(u∈[0,1],v∈[0,1])，S(u,v)通过所有截面曲线，并且达到C1光滑。

2.2 插值构造截面曲线

对于给定的截面数据，本方法构造截面曲线的过程为首先将每个截面上的数据点进行弦长参数化，然后将同一截面上每三个相邻的数据点进行插值，构造若干条待融合的曲线段；最后将相邻的曲线段两两融合，并把最终产生的融合曲线段首尾相接，产生光滑的截面曲线。

2.2.1 截面数据点参数化

本方法使用弦长参数化的方法进行数据点参数化，确定截面上各个数据点的参数值。取沿截面线的参数方向为u向，沿各截面排列的参数方向为v向。则Pi,j的参数值为：

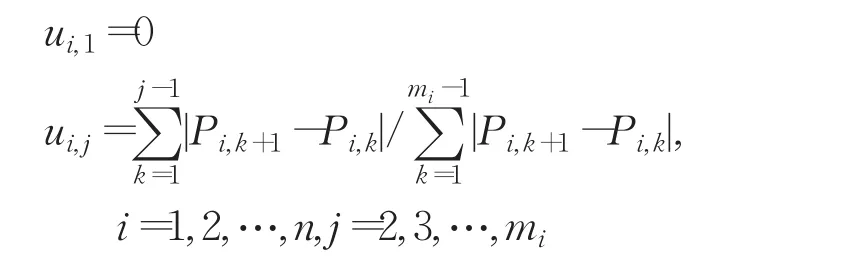
2.2.2 局部插值构造曲线段

随着插值数据点数的增加，高阶的多项式插值会出现龙格现象，产生剧烈的震荡。为了保证更精确的还原待建曲面上的自然形状，减少曲面上的扭曲和形变，本方法先对截面数据点进行局部插值构造曲线段，然后将其拼接得到截面线。依次将截面上所有相邻的三个数据点Pi,j,Pi,j+1,Pi,j+2进行插值，用Pi,j(u)表示得到的曲线段。公式如下：

其中，i=1,2,…,n,j=1,2,…,mi-2,u∈[ui,j,ui,j+2]。

2.3 构造融合曲线

传统方法中的曲线拼接需要获得待拼接曲线的切矢、导矢等微分信息，计算相当麻烦；基于融合思想的曲线拼接是指将起点与终点相同的若干曲线段直接通过融合函数进行融合，不需要边界的微分信息即可完成曲线的光滑拼接。本方法采用的融合函数如下：

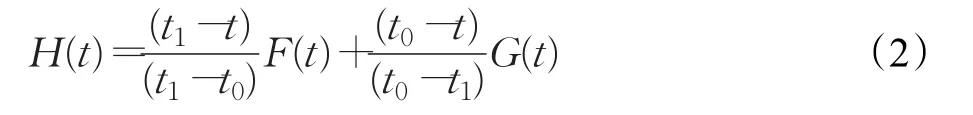
其中，F(t)和G(t)为待融合曲线，H(t)为融合后的曲线，t∈[t0,t1]。

使用公式（2）对上一步求得曲线段Pi,j(u)、Pi,j+1(u)的参数u方向上的公共部分进行融合，公式如下：

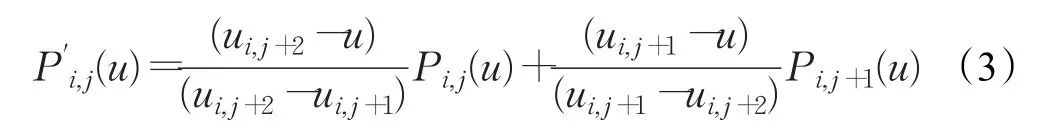
其中，i=1,2,…,n,j=1,2,…,mi-3,u∈[ui,j+1,ui,j+2]。

将公式（3）中得到的曲线段与Pi,1(u)上u∈[0,ui,2]的部分和Pi,mi-2(u)上u∈[umi-1,1]的部分首尾拼接，即可得到一条C1光滑的截面曲线，表达式为：

其中，i=1,2,…,n。

对于封闭的截面曲线同样可以使用该方法进行构造，只需在首尾相接的位置再插值一条曲线，然后按以上步骤进行融合即可。

2.4 融合曲面重建

NURBS曲面的构造方法为先将各截面曲线的节点矢量合并，得到公共节点矢量；然后通过反求控制顶点得到曲面的矩形网格，从而得到待建曲面。为避免节点矢量相容的过程，本方法先将相邻的三条截面曲线进行插值来构造曲面片，随后将相邻曲面片参数上的公共部分进行融合以完成拼接，从而得到待建曲面。

2.4.1 插值截面曲线构造曲面片

将各截面曲线进行v方向上的参数化，确定各截面曲线的参数值。公式如下：

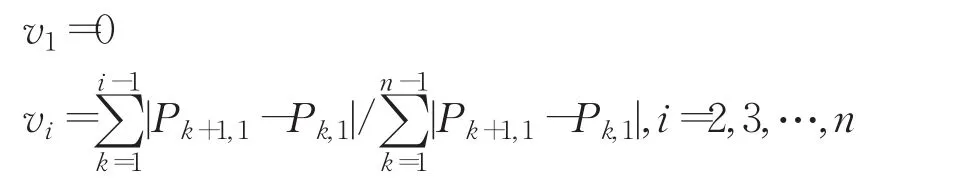
依次将每三条相邻的截面样条曲线进行插值，用Si(u,v)表示初步得到的曲面片。公式如下：

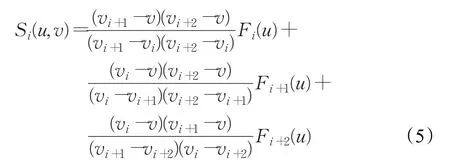
其中，i=1,2,…,n-2,v∈[vi,vi+2],u∈[0,1]。

2.4.2 构造融合曲面

传统的曲面拼接需要曲面的拼接部分切平面相同才能达到C1的连续，但是融合曲面的构造只需要两个曲面在参数域存在公共部分即可，而不需要考虑边界的信息，融合后得到的曲面根据融合函数的不同可以达到不同阶数的连续。将公式（5）中得到的曲面片的公共部分进行融合，然后将得到的融合曲面拼接，从而得到最终的待建曲面。本方法采用的融合函数如下：

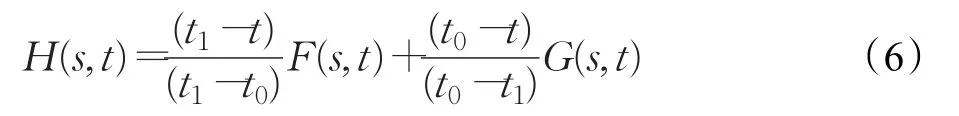
其中，F(s,t)和G(s,t)为待融合曲面，H(s,t)为融合后的曲面，t∈[t0,t1]。

使用公式（6）将公式（5）中求得的曲面片进行融合，公式如下：

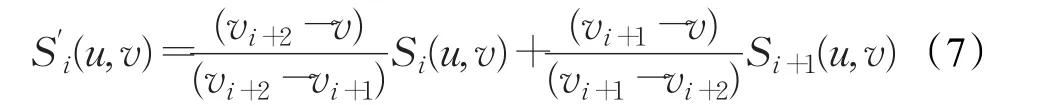
其中，i=1,2,…,n-3，v∈[vi+1,vi+2]，u∈[0,1]。

融合过程如图1所示，图1（a）中为用公式（5）插值相邻的截面曲线后得到的两个参数上存在公共部分的曲面片，图1（b）为施加公式（6）中的融合函数后得到的曲面片。

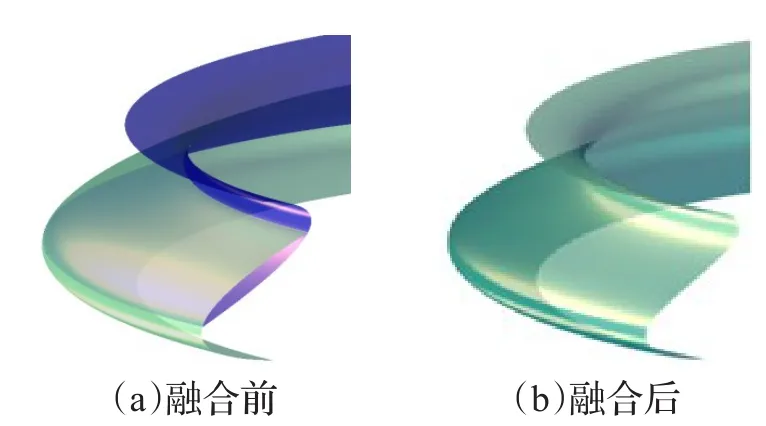
图1 曲面片的融合过程

3 算法应用实例及分析

为验证本算法的有效性，建立实验对一系列实物模型进行了曲面重建。图2为经过坐标测量机测量后得到的截面数据点，图3为经过本算法实现的应用实例。图3（a）、图3（b）为国际象棋的棋子的重建模型，图3（a）中的模型上有29行，共约1.22×103个数据点，图3（b）中的模型上有24行，共约1.08×103个数据点。从结果可以看出重建后的曲面光滑，原始模型的局部特征得以保留；图3（c）为一个花瓶的重建模型，该原始数据包含0.82×103个数据点，存在一定的噪音，重建完成后的曲面虽然存在些微形变，但是整体依然反映了原始模型的外形；图3（d）为一根弯管的重建模型，采样后得到约1.04×103个数据点，从实例可以看出该重建曲面形状得到了较好的控制，并且保证了曲面的光滑，没有出现明显的曲面形变和扭曲。

图4为一个箕型曲面的原始数据和通过本方法得到的重建结果，该原始数据有约2.29×103个数据点。如图4（a）所示，该原始数据的采样点数在各个轮廓上并不相等，并且分布很不均匀；从图4（b）中的融合曲面重建结果可以看到曲面表面光滑，并且没有出现明显的扭曲，从而证明了本方法在针对每行原始数据点数差距较大且分布不均匀时，能达到较好的重建效果。

图2 原始数据

图3 一组算法应用实例

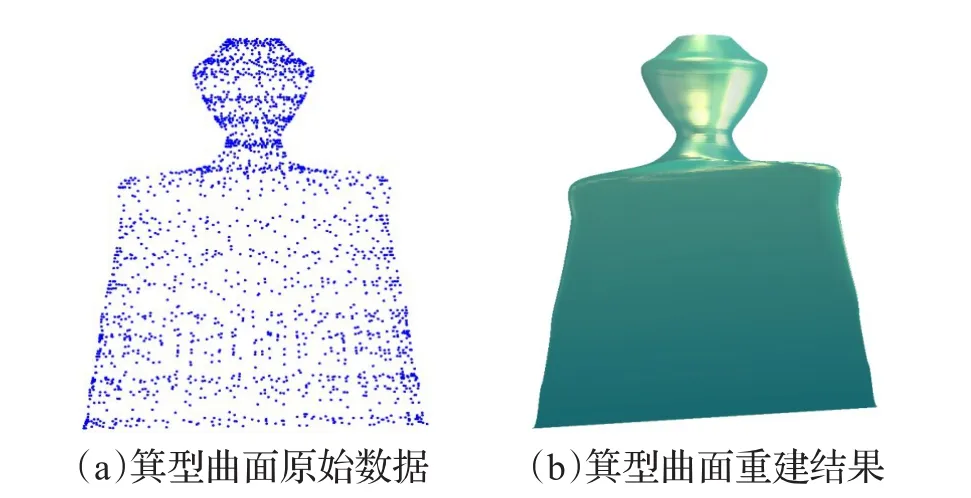
图4 箕型曲面重建实例

表1至表5显示的数据为基于几种方法将图2（a）～（d）、图4（a）中的原始数据进行曲面重建后得到的曲面上的数据点数的对比。本文以Piegl方法得到的曲面数据点数作为基准来判断各方法进行曲面重建后数据点数的冗余量减少效果。表中数据显示，当原始扫描数据点在每个截面上点数并不相同并且分布不太均匀时，本方法与Piegl等传统方法对比，数据量增长相对更少，而传统方法因为节点的大量增加导致了控制点数的膨胀，带来了较多的数据冗余。

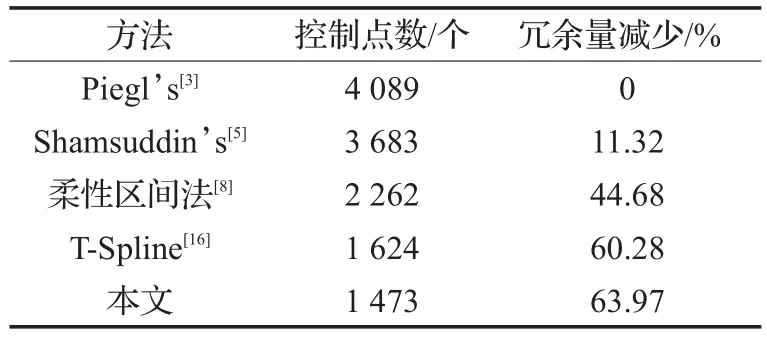
表1 图2（a）与几种方法数据冗余量减少的对比

表2 图2（b）与几种方法数据冗余量减少的对比

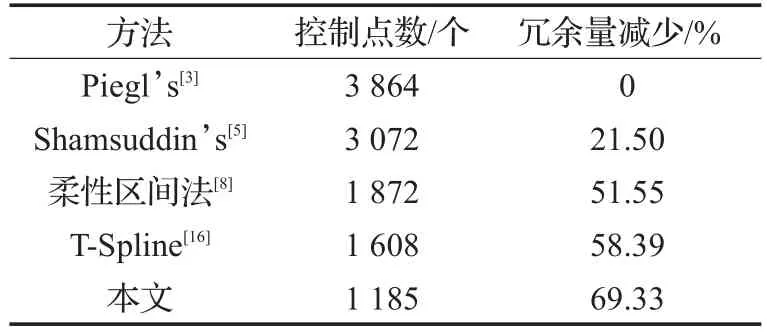
表3 图2（c）与几种方法数据冗余量减少的对比

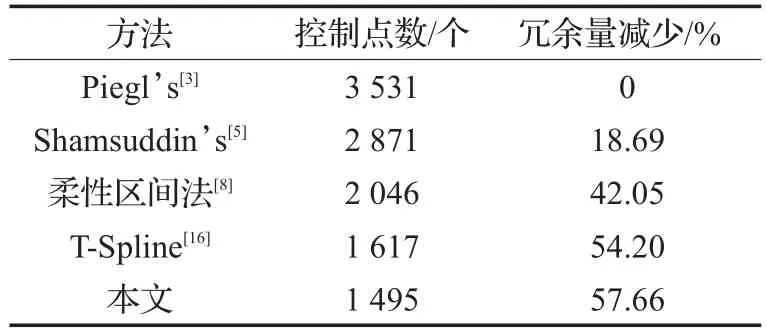
表4 图2（d）与几种方法数据冗余量减少的对比

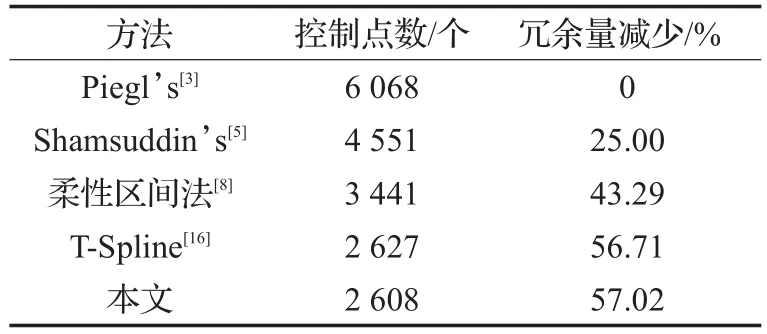
表5 图4（a）与几种方法数据冗余量减少的对比

表6为在实现了图2（a）～（d）、图4（a）中的曲面重建的基础上，使用Geomagic Studio软件提供的曲面偏差分析，将原物体的表面曲面模型与几种方法重建曲面的比较结果。从表中数据可以看出，融合曲面重建方法在大大减少了控制顶点冗余的同时，保证了待建曲面的重建精度，与已有方法相比并没有出现明显的误差量增加。

表6 曲面重建结果的重建精度对比

4 结束语

为了避免NURBS曲面构建过程中的节点矢量相容的过程，改善NURBS曲面控制点必须位于矩形网格上的缺陷，提出了一种双参数方向上融合插值的C1曲面重建方法，先后分段插值以构造曲线段、曲面片，采用了融合的思想进行曲线、曲面拼接，最后得到光滑的待建曲面。本方法虽然目前限于没有分支结构的曲面重建，但是依然可以用于拟合大量的实物模型。融合曲面的构造不需要考虑边界信息，可以直接进行曲面拼接，不仅能得到光滑的待建曲面，而且能够有效地减小计算量。

在将来的工作中，针对单个截面数据点列参数化时，如果数据点个数较少可能会引起截面线扭曲变形的问题，本方法将寻求一种更佳的参数化方法来提高精度；同时如何将本方法延伸到C2以至Cn精度的曲面重建，也是下一步值得探讨和研究的。

[1]Kim S U，Lee C O.Accurate surface reconstruction in 3D using two-dimensional parallel cross sections[J].Journal of Mathematical Imaging and Vision，2015，53（2）：182-195.

[2]Holloway M，Grimm C，Tao J.Template-based surface reconstruction from cross-sections[J].Computer&Graphics，2016，58（1）：84-91.

[3]Piegl L A，Tiller W.Surface skinning revisited[J].Visual Computer，2002，18（4）：273-283.

[4]Liu S，Jacobson A，Gingold Y.Skinning cubic Bezier splines and Catmull-Clark subdivision surfaces[J].ACM Transactions on Graphics，2014，33（6）：1-9.

[5]Shamsuddin S M，Ahmed M A，Samian Y.NURBS skinning surface for ship hull design based on new parameterization method[J].InternationalJournalofAdvanced Manufacturing Technology，2006，28（9）：936-941.

[6]曲学军，宁涛，席平.逆向工程中平面轮廓线数据的B样条曲面拟合[J].计算机工程，2004，30（10）：14-19.

[7]Wu Xiaogang，Chen Dan，Zheng Chunying.Flexible skinning research in reverse engineering based on cross-sectional fitting[C]//Proceedings 3rd International Symposium Computer Science&Computational Technology，2010：373-375.

[8]郭伟青，李际军，吴小刚.逆向工程中扫描数据点的曲面重构[J].计算机集成制造系统，2004，10（9）：1160-1164.

[9]Park H，Kim K，Lee S C.A method for approximate NURBS curve compatibility based on multiple curve refitting[J].Computer-Aided Design，2000，32（7）：237-252.

[10]Park H.Lofted B-spline surface interpolation by linearly constrained energy minimization[J].Computer-Aided Desigh，2003，35（14）：1261-1268.

[11]Zhang Xia，Zhao Jibin，Liu Weijun，et al.Skinning surface algorithm of B-spline for scattered point cloud[C]//2011 International Conference on Consumer Electronics，Communications and Networks，2011：2617-2620.

[12]林子植，潘日晶.基于轮廓数据的B样条曲面重建[J].计算机工程与应用，2008，44（19）：59-62.

[13]Sederberg T，Zheng J，Bakenov A，et al.T-splines and T-NURCCS[J].ACM Transactions on Graphics，2003，22（3）：477-484.

[14]李新.T样条和T网格上的样条[D].合肥：中国科学技术大学，2008.

[15]Yang Xunnian，Zheng Jianmin.Approximate T-spline surface skinning[J].Computer-Aided Design，2012，44（12）：1269-1276.

[16]Li Yusha，Chen Wenyu，Cai Yiyu，et al.Surface skinning using periodic T-spline in semi-NURBS form[J].Journal of Computational and Applied Mathematics，2015，273（1）：116-131.

[17]Wenz R.Interpolation of curve data by blended generalized circles[J].Computer Aided Geometric Design，1996，13（8）：673-680.

[18]Majeed A，Mt Piah A R，Ridzuan Y Z.Surface reconstruction from parallel curves with application to parietal bone fracture reconstruction[J].Plos One，2016，11（3）.