林业运动模糊图像复原的融合正则化方法

赵汐璇，阚江明

北京林业大学 工学院，北京 100083

1 引言

林区立地条件十分复杂，林业机器人（工程装备）一般属于大型装备，在林区行走作业时很容易发生一些小幅的无规律运动（包括在松软或者潮湿林地上发生的滑动、碰撞障碍物产生的振动和不平路面的颠簸）。而林业机器人的作业机械臂长达8 m，相机安装在作业机械臂的末端，这些小幅的无规律运动很容易造成林业机器人视觉系统获取的图像产生运动模糊，这会影响后续的识别、三维重建和测量精度等工作。林业机器人无规律运动情况极为复杂，并且是必然会发生，不可忽视的。针对这一问题，对林业机器人无规律运动条件下的运动模糊图像复原这一非常具有挑战性且有很大应用价值的图像盲复原问题进行了研究。

由于图像盲复原问题是一个不适定性问题，这就导致了求解这个问题时可能会获得无穷多的近似解。因此，怎样从众多的近似解中找出最优解是图像盲复原技术需要解决的主要问题。在以往的研究中，常使用正则化技术来解决这个问题。其思想是通过在代价函数中增加问题的正则化约束项，将不适定问题转化为适定的问题[1]。通过怎样的正则化约束项来构造代价函数，成为研究的关键问题。麻省理工学院Fergus等[2]通过高斯模型近似自然图像的梯度的重尾分布，构建图像恢复过程的正则项。但由于近似误差的存在，使得图像复原结果在结构上不够精确，同时振铃效应较为严重。

为了克服恢复出的清晰图像中含有振铃效应的问题，Shan等人[3]考虑了自然图像的全局先验和局部先验。在局部通过限制模糊图像与复原图像的梯度相等来构造正则项约束，并采取连续的分段一次和二次函数拼接的正则项来逼近全局图像的重尾分布。这一方法很好地抑制了振铃效应。但存在细节信息损失以及噪声的问题。

Krishnan等[4]构造了自然图像高频部分L1范数与L2范数比值的归一化算子，这一算子可以得到与清晰图像相仿的能量，并且具有尺度缩放不变性。他们发现图像模糊程度越大这一归一项值相应增大，并且这一算子在高频部分与L1有相同效果。因此可通过构造最小化函数约束这一正则项达到去模糊的效果。

目前应用字典学习及稀疏表示的技术进行图像盲复原是图像复原领域的热点。Elad等人[5]分别构造了基于大量采集图像的字典和基于模糊图像本身的字典，然后通过约束字典系数的稀疏性和字典复原图像的接近度正则项构建最小化函数。提出通过KSVD算法来求解复原图像的方法，取得了很好的效果。

Li将稀疏表示正则项应用到盲图像去模糊模型中，同时估计原始图像、模糊核及稀疏系数，三者交替进行[6]。Yin等认为，无论图像清晰与否，用给定的字典对图像进行稀疏表示，表示的系数是相同的[7-8]。Li等从模糊图像中估计模糊核，然后基于图像在过完备字典中表示的稀疏性，通过用清晰字典更新模糊字典去除图像模糊[9]。

受以上文献的启发，考虑能否提出一种运动模糊图像复原方法能够充分利用图像的全局和局部信息，将上述文献的优势结合起来。以此为出发点，本文提出了一种融合的正则化林业运动模糊图像复原算法。先通过引入L1范数与L2范数比值的正则项，求解模糊核，将图像盲复原问题转化为非盲复原问题，再引入图像超拉普拉斯先验正则项及稀疏表达正则项，对复原图像进行求解。引入的稀疏表达正则项可以利用先验字典丰富的信息以及每一图像小块包含的局部信息。而L1/L2范数、超拉普拉斯正则约束项，可以很大程度上约束整幅图像中的高频信号，充分利用林业图像中大量的边缘信息，并且对稀疏表示正则项容易产生块效应的问题进行很好的弥补。最后，分别对人工合成的运动模糊图像及自然采集运动模糊图像进行了实验，并和其他方法进行了比较，实验结果表明了本文方法的有效性。

2 方法概述

在林业作业环境中，林业机器人相机抖动产生的运动模糊图像的数学模型为：

其中，f为待求清晰图像，林业机器人作业机械臂运动数学模型记为k，林业机器人作业环境噪声模型记为n，林业机器人在有噪声条件下获得的模糊活立木图像为g。本文研究的目标是通过已获得的运动模糊图像g，求解运动模糊核K，复原未知的清晰图像 f。

为了解决上述问题，本文提出了林业运动模糊图像复原的融合正则化方法。

3 算法步骤

本章将对本文提出的融合L1/L2范数及图像梯度先验约束的稀疏正则化去运动模糊方法进行详细地阐述，下面将依次对算法流程中的每一步进行介绍。

3.1 初始化图像

本文中，采用文献[5]中稀疏表达的方法对图像去噪，用运动模糊图像本身进行字典训练。这样可以重构出一幅去噪图像将其作为初始化图像。

3.2 运动模糊核的盲估计

L1范数常被用来惩罚高频带信息，图像噪声多处于高频带部分，因此限制L1范数使之达到最小，是图像去噪的一种方式[10]。L1/L2正则项可以被看做L1范数的归一项，并且L1/L2正则项还具有尺度不变性。当用于图像时，它既有L1范数能根据图像全部能量对边缘尺度进行调整的作用，并且满足与模糊程度的正相关关系。因而L1/L2正则项可以在高频域很好地区分清晰、模糊图像，很适用于图像去模糊的问题。因此，采用文献[4]提出的L1/L2正则项来构造代价函数，约束求解模糊核。

构造代价函数：

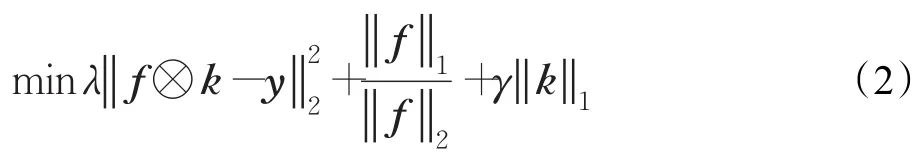
其中第一项保证了复原图像与原始图像的接近度，第二项是对 f的L1/L2正则项，保证了复原过程中尺度不变的稀疏性，第三项是为减少模糊核噪声，对模糊核的约束项，其中k满足总和为1，且非负。λ、γ为权重系数，确保了模糊核和图像正则项之间的相对权值。

由于式（2）是高度非凸，对其进行求解最常用的方法是交替更新 f和k进行求解。

3.2.1 f的更新

首先，初始化一个模糊核k，固定k，求解 f。即求解：

由于项的存在，使得这一问题成为一个非凸问题。通过将前一步迭代得到的 f的L2范数值代入式（3），使其转化为一个求解式（4）的凸的L1正则项的优化问题：

L1正则项的优化问题，是压缩感知领域中常见的问题，有很多解决方法。本文中，采用迭代阈值收缩算法（ISTA算法）对本问题进行求解。在完成对 f的更新后，下一步就是实现对模糊核k的更新。

3.2.2 k的更新

代入3.2.1小节计算得到的清晰图像 f的估计值，对模糊核k进行求解，式（2）即可转化为求解：

其中，模糊核满足约束条件k≥0,∑iki=1。可以采用非约束的迭代重加权最小二乘（IRLS）方法进行求解。IRLS算法中转化为方程求解的步骤，只需采用几步共轭梯度（CG）算法即可实现。

同时，本文采用了文献[11-12]中对模糊核的处理方法，对在最细尺度求得的模糊核进行阈值限制，使得值较小的部分置为零，这可以增加模糊核对噪声的鲁棒性。

3.2.3 多尺度的实现

采用文献[11]中多尺度模糊核的估计方法，构造由粗糙到精细的图像分辨率金字塔。在每一尺度都对 f和k进行200次交替更新。以 2的采样率通过双线性插值方法对图像进行采样，获得图像金字塔。设定初始模糊核大小为3×3。每一层计算出的清晰图像估计值f和模糊核k均作为下一层金字塔的初始值。

3.3 清晰图像的非盲复原

在求出模糊核k后，问题转化为非盲图像复原的问题。本文中通过建立结合超拉普拉斯梯度分布约束及稀疏表达约束的代价函数，以最小化代价函数为求解目标，对复原图像进行求解。超拉普拉斯梯度分布信息包含了图像的全局信息[13]，这可以有效抑制仅采用稀疏编码会产生的人工块效应[14]，并发挥出稀疏表达在计算速度，表达形式上的优势。

构造代价函数

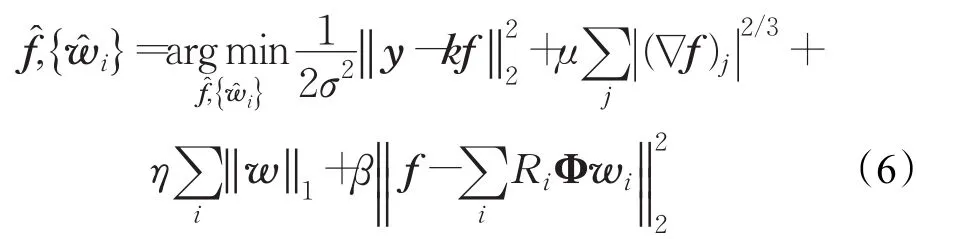
其中μ、η、β为权重系数，第一项保证了复原图像与原始图像的逼近程度，第二项为图像超拉普拉斯正则约束项，可保证自然图像的长拖尾分布[13]，第三、四项共同构成了字典稀疏先验约束项，Φ为通过对大量清晰图像进行在线字典学习得到的字典，Ri表示图像小块的位置信息[14]。由于超拉普拉斯梯度先验项和字典稀疏先验项的存在，使得这一问题是非凸的。需要通过交替更新 f和{wi}的方法进行求解。

3.3.1 w的求解

首先固定 f，式（6）的问题可以转换为：

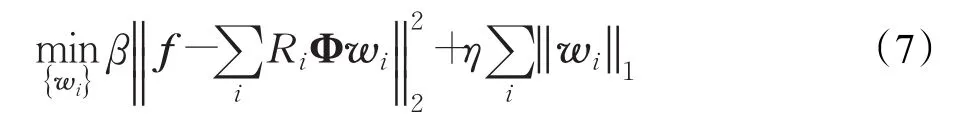
对于每一个图像小块，即需求解：

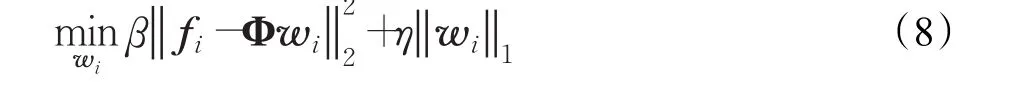
这是一个L1范数的最小化优化问题，有许多方法可对其进行求解。本文采用LASSO算法[15]对其进行求解。

3.3.2 f的求解

代入3.3.1小节求得的w的值，求解最优化 f的解的问题，是一个较为复杂的非凸问题。式（6）的代价函数转化为求解如下问题：

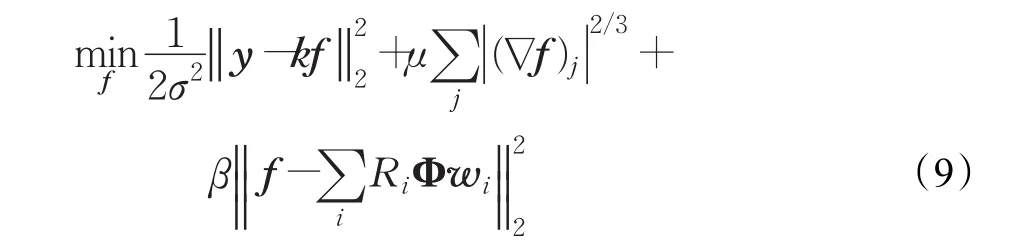
文献[16-17]给出了一种很好的解法。首先，引入一个辅助系数Z，将微分算子∇和L2/3伪范数分离，方便求解。式（9）可转换为：

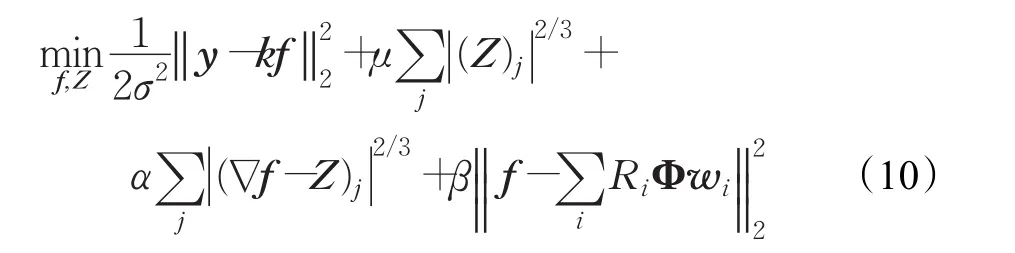
此时，随着α→∞式（10）的解收敛于式（9）的解。本文首先设定α的一个初值αmin，再以增益q不断增加，直至达到设定阈值αmax。给定一个α，式（10）可通过先固定一个变量求解另一个的方式，交替更新 f和Z。在实际应用中，对每个α值，仅需交替更新一次 f和Z即可满足要求。

（1）固定Z和α，最优的 f满足：

其中U=∑iRiΦwi，I为单位矩阵。采用文献[3]中的方法，对式（11）进行二维快速傅里叶（FFT）变换，整理式子可得解为：

其中d为相应于∇的二维卷积核。

（2）固定 f和α，最优的Z可通过下式求解：

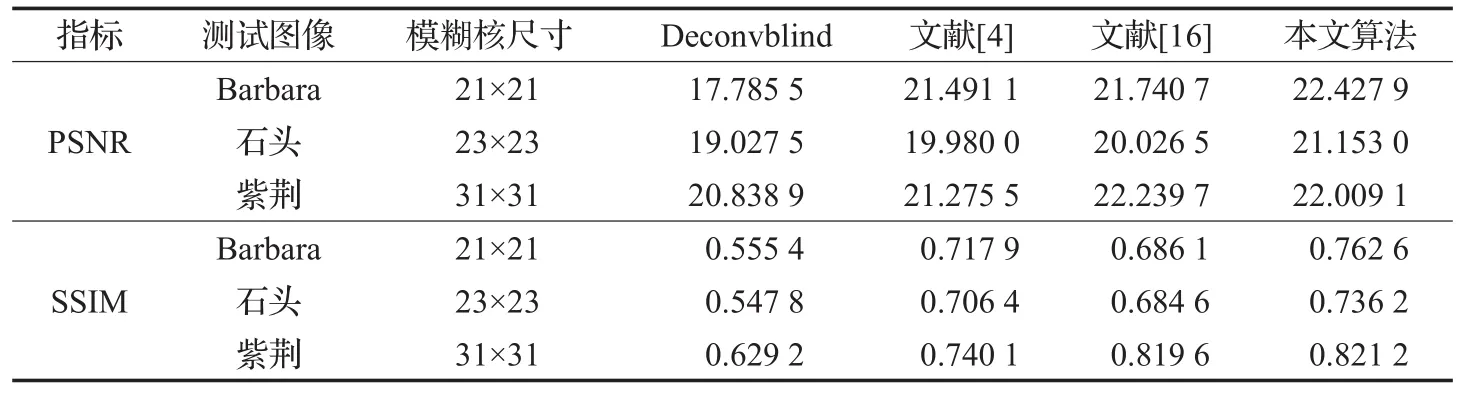
表1 不同方法模糊图像复原指标比较

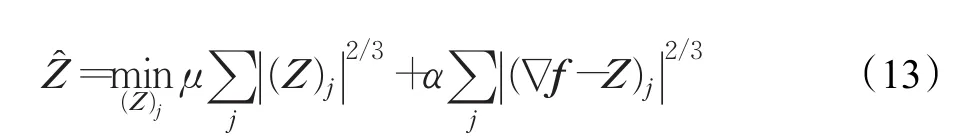
对Z求导，得到一个一元四次方程：

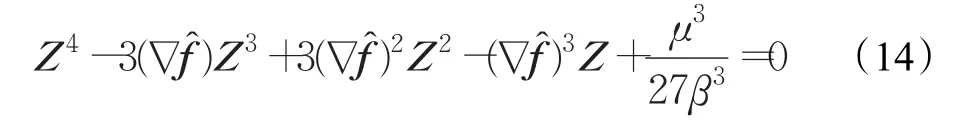
采用文献[13]提出的基于分析的方法可快速获得方程（14）的一个根，即为Z的解。

由于随着α→∞，式（10）的解收敛于式（9）的解，因而求得的Z的值即为所求 f，至此，得到了本文算法恢复得到的去运动模糊清晰图像 f。

4 实验结果

为了验证本文算法的可行性和性能，首先对人工合成的运动模糊图像进行了实验，由于人工合成的运动模糊图像的模糊核、原始清晰图像均已知，方便用客观的评价指标对算法复原的图像进行评价。本文选取了两项较为常用的评价指标对算法的复原结果进行评价。峰值信噪比（PSNR）是最普遍、最广泛使用的图像质量评价指标，不过许多实验结果都显示，PSNR的分数无法和人眼看到的视觉品质完全一致，因而采用峰值信噪比（PSNR）和结构相似度（SSIM）[18]这两项指标对图像复原的效果进行了评价。这两项指标均由原始清晰图像和算法复原图像对比得到，值越高代表图像复原效果越好。

在验证了本文提出的算法的有效性后，又对自然条件下真实运动模糊图像进行了实验，并与Matlab自带的deconvblind图像盲复原函数以及文献[4]、文献[16]这三种图像盲去模糊算法进行了对比。由于真实运动模糊图像的原始清晰图像不可知，在这一部分通过放大细节的方式对几种复原算法的结果直接进行比较。

4.1 人工合成运动模糊图像复原实验

首先通过Matlab平台，对采集得到的清晰图像进行逆时针以15°方向运动20个像素的模糊处理，再比较不同算法与本文算法对模糊图像进行复原的结果。选取了一张图像处理领域常用的图片以及采集得到的细节丰富的两张林业图片进行了分析实验。

由于估计模糊核尺寸的设定值对实验结果有很大影响，为保证实验的公平，对四种算法均设定相同的估计模糊核尺寸。其他参数也均为文献中设定好的参数。复原结果的平均PSNR评价指标和平均SSIM评价指标结果如表1所示。图1、图2分别展示了不同算法对测试图像“Barbara”和“石头”的复原结果。

图1 “Barbara”图像复原结果

图2 “石头”图像复原结果

通过实验结果，本文算法复原的测试图像的平均PSNR指标比文献[4]以及Deconvblind算法要高出很多，具有明显优势，相较于文献[16]的PSNR指标相差不多，根据图像特征的不同，有时会略低于文献[16]的值。但比较结构相似性的平均SSIM指标的结果，可以得到本文算法SSIM指标均高于其他三种算法，有很好的优势。结构相似度指数反映了场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合[18]。这一指标能够很好地体现图像具体的细节信息，细节信息丰富也是林业图像的一个重要特征。因而这也表明，本文算法的复原效果细节更加清晰，复原效果十分理想。

图3 自然条件下真实运动模糊图像复原结果及局部放大图

通过观察实验复原结果，从视觉效果上来看，Deconvblind函数复原出的图像始终有一层“薄雾”，图像整体依然存在明显的模糊。文献[4]复原出的图像细节比较清晰，但在图像的边缘存在比较明显的“振铃效应”。文献[16]运行出的结果在图片中有很明显的“波纹”存在，存在明显的“振铃效应”。而本文提出算法得到的复原图像相较于其他三种算法，图像光滑，细节清楚，边缘清晰，没有明显的“振铃效应”。因而，在视觉效果上本文算法也优于其他三种算法。

根据以上评价指标及人眼视觉感受，本文算法具有很好的可行性，并具有优良的性能，图像盲复原效果优于其他对比算法。

4.2 自然条件下真实运动模糊图像复原实验

为了进一步验证本文算法的有效性和性能，在这一部分，本文选取了自然条件下真实运动模糊的图像进行实验对算法进行了测试。选取了其中一幅测试图像的复原结果展示如图3所示。将红色方框部分放大，展示到对应种算法复原图像的下方，可以更清楚地看到图像复原的细节。本文算法估计的模糊核如图4所示。

图4 本文算法估计的模糊核

由图3可以看出，本文提出的方法同样可以复原自然条件下真实运动模糊图像，并取得较好的效果。本文的算法与Deconvblind相比复原效果明显更优，去除了明显的模糊，且复原的图像细节十分清晰。与文献[4]、文献[16]复原的结果相比，这两种算法或多或少地存在“假边缘”现象，可以明显看到树干的花纹以及细碎叶片的边缘有“白线”或“白点”存在，而本文算法没有出现明显的“假边缘”现象，且细碎叶片的边缘及树干纹理均十分清晰。需要注意的一点是，自然条件下真实运动模糊图像的往往会引入一些非线性的模糊过程、空间变化的模糊以及未知的噪声等等，它们都会对复原图像的质量产生严重的影响[19]。

5 结束语

林业机器人在林区作业时，不可避免地会发生小幅无规律运动，这会容易导致采集图像产生运动模糊，影响后续对图像信息的提取。针对这一问题，本文提出了林业运动模糊图像复原的融合正则化方法，融合了L1/L2范数及超拉普拉斯约束的稀疏表达正则项。本方法充分利用了L1/L2范数能量、尺度缩放不变性，超拉普拉斯正则项对林业图像中大量边缘信息的约束，以及稀疏表达对先验字典信息的利用率。首先，通过L1/L2范数正则项构造代价函数，将图像盲复原问题转化为非盲复原问题。再通过拉普拉斯正则项及稀疏正则项，构造图像复原代价函数，复原出清晰图像。最终实验结果显示出本文提出的运动模糊图像复原方法优于其他三种对比方法，复原结果在视觉上也更符合人眼的视觉感受[19]。

[1]马彦中.基于正则约束的运动模糊图像盲复原研究[D].沈阳：东北大学，2014.

[2]Fergus R，Singh B，Hertzmann A，et al.Removing camera shake from a single photograph[J].ACM Transactions on Graphics，2006，25（3）：787-794.

[3]Shan Q，Jia J，Agarwala A.High-quality motion deblurring from a single image[J].ACM Transactions on Graphics，2008，27（3）：1-10.

[4]Krishnan D，Tay T，Fergus R.Blind deconvolution using a normalized sparsity measure[C]//IEEE Conference on Computer Vision and Pattern Recognition，2011：233-240.

[5]Elad M，Aharon M.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Transactions on Image Processing，2006，15（12）：3736-3745.

[6]Li L，Kan J M，Wu Y X，et al.Motion blurred images restoration based on sparse regularization[J].International Journal of Applied Mathematics&Statistics，2013，51（24）：1-10.

[7]Yin M，Gao J，Tien D，et al.Blind image deblurring via coupled sparse representation[J].Journal of Visual Communication&Image Representation，2014，25（5）：814-821.

[8]Hu Z，Huang J B，Yang M H.Single image deblurring with adaptive dictionary learning[C]//International Conference on Image Processing，Hong Kong，China，2010：1169-1172.

[9]Li L，Zhang R，Kan J，et al.Image deblurring via an adaptive dictionary learning strategy[J].Telkomnika，2014，12（4）：855-864.

[10]Levin A，Weiss Y，Durand F，et al.Understanding and evaluating blind deconvolution algorithms[C]//IEEE Conference on Computer Vision& Pattern Recognition，2009：1964-1971.

[11]Freeman W T，Fergus R D W，Singh B，et al.Removing camera shake from a single photograph，US20080025627[P].2008.

[12]Whyte O，Sivic J，Zisserman A，et al.Non-uniform deblurring for shaken images[J].International Journal of Computer Vision，2012，98（2）：168-186.

[13]Krishnan D，Fergus R.Fast image deconvolution using hyper-Laplacian priors[C]//International Conference on Neural Information Processing Systems，2009：1033-1041.

[14]Aharon M，Elad M，Bruckstein A.-SVD：An algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing，2006，54（11）：4311-4322.

[15]Efron B，Hastie T，Johnstone I，et al.Least angle regression[J].Mathematics，2004，32（2）：407-451.

[16]Xu L，Zheng S，Jia J.Unnatural L0 sparse representation for natural image deblurring[C]//IEEE Conference on Computer Vision&Pattern Recognition，2013：1107-1114.

[17]Jia C，Evans B L.Patch-based image deconvolution via joint modeling of sparse priors[C]//IEEE International Conferenceon ImageProcessing，Brussels，Belgium，September 2011：681-684.

[18]Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment：From error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13（4）：600-612.

[19]唐述，龚卫国，仲建华.稀疏平滑特性的多正则化约束图像盲复原方法[J].软件学报，2013，24（5）：1143-1154.