基于密度二分法的密度峰值聚类方法
2018-06-26许朝阳林耀海
许朝阳,林耀海,张 萍
1.莆田学院 信息工程学院,福建 莆田 351100
2.福建农林大学 计算机与信息学院,福州 350002
1 引言
近年,密度峰值聚类方法(Density Peaks Clustering,DPC)[1]得到了广泛的研究和应用,例如,在电力消费行为的聚类[2],文本聚类[3],无监督的声学单词发现计算[4],批处理建模和在线监测[5],医疗数据[6],城市出租车热点区域发现[7],异常值检测[8]和超光谱段选择[9]等领域。密度峰值聚类方法以它不需要迭代、不需要太多参数等优点,备受欢迎。
学者们也对密度峰值聚类方法本身做了一些改进,以适应应用领域中的新情况,包括在聚类中心的判断,截断距离dc的选择,密度计算方法的修改等。如Ma等在文献[10]中设定,并按照从大到小排列,取前m个最大值作为聚类中心,Mehmood等提出了一种模糊CFSFDP方法[11],用于有效地自适应地选择聚类中心;Wang和Xu[12]引入了一种基于熵的截断距离dc的选择方法;Wang等[13]使用多变量的核密度估计方法自动选择截断距离dc。Mehmood等[14],基于热方程,使用另一个非参数密度估计器进行密度估计;Yan等[15]提出了基于点与其第k个最近邻点之间的距离(称为半径)来估计每个点的局部密度。Du等[16]在高维数据点情况下使用PCA降维,然后在降维后的空间中使用KNN计算每个点的密度。高诗莹等[17]通过计算数据样本中的密度比,以避免低密度的类在决策图上被遗漏,从而提高聚类准确率。李建勋等[18]充分利用属性数据提高聚类质量。
密度峰值聚类方法基于这样的假设:聚类中心被邻近地区密度较低的邻居所围绕,并且与具有更高局部密度的任何点具有相对较大的距离。但密度峰值聚类方法确实存在一些缺点。作为聚类中心的数据点密度的差异程度,是影响密度峰值聚类方法聚类效果的一个关键原因。包含两个方面:不同类的数据点密度差异过大,同一类中多个密度聚类中心密度值差异过小。已有的方法,有的没考虑到这些问题,有的只处理了一种情况,而本文方法能够较好地兼顾两种情况的处理。
在上述问题中,数据点的密度不均衡是个关键,因此,本文提出了基于数据点密度二分法的密度峰值聚类方法。首先,将聚类过程视作两部分:聚类中心的确定、其他数据点归并到相应聚类中心。相应的,在本文算法中将数据分为高密度点和低密度点。一方面,对高密度的点进行聚类,根据决策图识别出聚类中心;另一方面,根据本文提出的分配策略,使高密度点和低密度点都归并到合适的聚类中心,从而实现聚类。
2 相关研究与问题分析
2.1 基于k-近邻与聚合策略的自适应密度峰聚类
基于k-近邻与聚合策略的自适应密度峰聚类(ADPC-KNN)[19]所针对的问题是,密度峰值聚类方法所提出的dc的确定方案,难以适应众多类型的待聚类数据;该文章指出,dc的确定需要考虑到每个数据点的k近邻距离,并与所有数据点的k近邻距离、k近邻距离的标准差都正向相关。其具体的公式描述如下:

其中N是数据点的数量,是点i和k最近邻居之间的距离,定义如下,=maxj∈KNNi(dij),μk是其中定义的所有点均值:
文献[19]提出了新的dc确定方案,然后基本沿用密度峰值聚类方法计算δi和ρi。为了克服由于同一个类中存在多个峰值点,而被划分为多个类,该文献还提出了数据归并算法。它拓宽了聚类间的密度核心类和类之间的边界(异常值)。在聚类中心的判断上,它将δi大于平均值的点作为初始的聚类中心之后,利用密度可达作为条件判断,将满足该条件的合并为一个类。它的不足是,对于类与类之间距离较小但有明显边界的类,也常被误判为同一类。同时,由于该归并算法将所有密度大于密度均值的点都作为可能的密度中心,然后进行迭代归并、判断,因此,算法复杂度较高。
2.2 基于密度归一化的密度峰值聚类
基于密度归一化的密度峰值聚类(DNDPC)[20]所针对的问题是,当不同类的数据的密度差异过大时,低密度的聚类中心难以通过密度峰值聚类方法的决策图识别出来。该文的解决思路是,用当前点的最近30个邻居的密度均值进行密度归一化后,代替当前点的密度值ρi,用ρ'i在决策图中辅助判断聚类中心点。其归一化公式描述如下:

其中,ρi表示点i的密度,定义如公式(3);Dinn表示当前点i的30个最近邻。归一化密度仅用于选择聚类中心。其他非中心数据的处理,仍以原始密度的决策图上的关系为基础。这种归一化密度的思路,使得低密度的中心点能有比原来密度峰值聚类方法更多的机会,从决策图中被识别出来。但是,同一类数据点中存在多个密度峰值而被误判的情况仍然是文献[20]没有解决的一个问题。

2.3 关键问题分析
当密度峰值聚类方法对同一批待聚类数据中各个类的密度差异过大,或者不同批次待聚类的数据密度差异过大,通过密度峰值聚类方法的决策图难以得到聚类中心,或者同一个类中产生多个聚类中心。这是影响密度峰值聚类方法得出准确聚类结果的一种常见情况。
如果这个问题没有得到有效处理,往往可能产生诸多的错误聚类。例如,密度较大的类可能被划分为多个类,或密度较大的类与其他类合并,或同一个聚类中包含多个密度中心。如图1(a),来自于Compound数据集,内圆和外圆应该属于不同类,但是由于外圆具有多个高密度点,并且比内圆的密度高,导致内圆被错误归类到外圆的类上如图1(c)。如图1(b),来自于Jain数据集,上面的圆弧和下面的圆弧也应该属于不同类,但是由于密度不同,导致错误的聚类结果,如图1(d)。
针对这种情况,学者们给出的方法[19-20]能够某种程度上解决这个问题,但仍有所不足(如2.1、2.2节的分析)。本文基于这两个工作给出的工作结果和分析角度,既要使dc根据数据的特征而作相应变化[19],也要使得密度峰值聚类方法能够兼顾到低密度数据在聚类过程中容易被忽视的情况[20]。
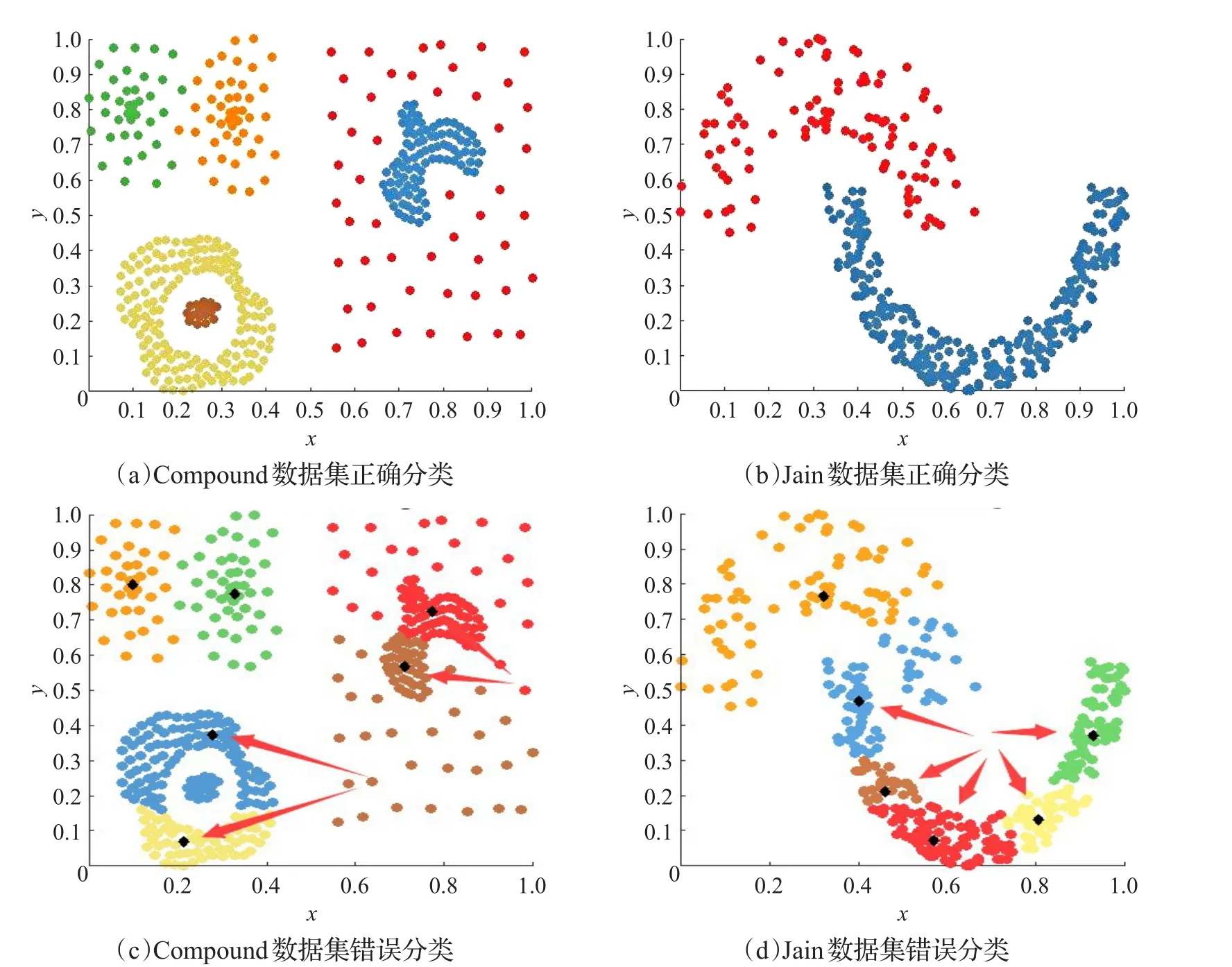
图1 密度不均衡数据集的聚类情况
因此,本文将聚类过程视为两个步骤:产生聚类中心、将数据点聚类到最为合适的聚类中心。相应的,求出所有数据点的密度平均值后,将数据点分为高密度数据点和低密度数据点。正因如此,本文所提方法称为“基于数据点密度二分法的密度峰值聚类”。在聚类之前去除低密度的点。然后对高密度的点进行聚类,使用一维高斯离散点检测,识别出聚类中心。分别对高密度点和低密度点提出了两个新的分配策略。
除了将数据分为高密度、低密度以便得到更好的聚类结果以外,本文的另外一个创新点是,本文认为在使用密度峰值聚类方法得到聚类结果后,要有相应的归并策略。如图2所示,上图被正确识别为两类,下图由于存在一条稀疏的数据带,在实际应用中很可能需要被识别为同一类。而到达到这个效果,就需要对密度峰值聚类方法的识别结果进行归并。
3 基于数据点密度二分法的密度峰值聚类方法
本文所提的基于数据点密度二分法的密度峰值聚类方法,包含以下内容:(1)基于k个最近邻居提出了截止距离dc的定义及计算;(2)基于一维离散点检测算法,能够有效和正确地发现密度峰值(聚类中心);(3)介绍了高密度点和低密度点的聚类分配新策略。这些新策略是连续应用的。

图2 两类数据需要归并的情况
3.1 截断距离和数据点二分法
为了使得dc能够根据数据集的不同形态而作相应修改,本文所提方法中dc的计算,参考了文献[19]。由于本文所提方法的dc主要用于对高密度数据点计算聚类中心,数据集更少,数据密度更高(相对于还未将数据分为高密度和低密度时的数据集),所以本文的dc在公式(1)的基础上乘以一个系数a。经过多次实验对比,系数a为0.25时效果最好。
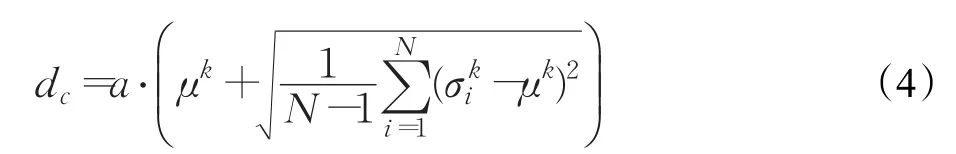
然后在密度峰值聚类方法的框架下,利用公式(3)计算 ρi。
本文高密度和低密度的分界值为全体数据点的密度值的均值,计算公式如公式(5):

然后,将点的密度值大于密度分界值ρˉ的点为高密度点,点密度值小于密度分界值ρˉ的点为低密度点。
3.2 聚类中心的计算
先对高密度数据点进行处理,计算出它们的聚类中心。
密度峰值聚类方法本质是一个二维度量的聚类算法,除了计算每个点的密度峰值之外,还需要计算每个点的距离,距离的定义如下:

根据密度和距离的值,计算γi的值

DPC算法的提出者[1]给出的选择聚类密度中心的方法是,通过人机交互的方式;也有众多学者对如何选择合适的聚类中心给出了自己的方案[10-11],由于这个不是本文的研究重心,这里选择的方案是在正态分布的假设下,如果i对应γi的值大于所有数据点的γ方差的3倍,那么i就可以被认为是一个聚类中心点[21]。聚类中心点构成一个集合,用C表示。

3.3 数据点分配策略
本文所谓的分配策略是指,在确定完聚类中心点以后,将每个点与最合适它的聚类中心点联系起来。从而,实现最终的聚类过程。
数据点的分配策略有两种,分别适用于高密度点和低密度点。
总体上来说,对高密度数据点的分配策略仍用原密度峰值聚类方法算法的方式。根据高密度点得到的决策图,会求出一系列的聚类中心点。整个数据集的聚类中心,也将在这一系列聚类中心中产生。为了后续将其他非聚类中心点归并中相应的聚类中心上,将上述这一系列聚类中心进行编号。对于密度最高的点,设置分配编号值为0;从密度第二大的点开始,设置分配编号值为密度比它大并且距离最小的点的编号。该分配策略优先考虑密度比较大的点,而后再寻找距离小的点。
与高密度点的分配策略不同,对于低密度点的分配策略需要同时考虑密度和距离两个因素。所以,定义了归属概率,用来表示,如公式(9)。低密度点i的分配策略是,分配到归属概率比i大的相邻点。

其中wij定义为代表点i和 j之间的相似度wij,这意味着点i和 j之间的距离越小,它们越相似。并将它们归一化。
除此以外,还作了密度中心合并策略,以避免同一个类中,由于存在多个峰值,而被错误划分。首先,定义了两个点的dc可达,即这两个点在所有的高密度点间存在一条路径,该路径上的点的两两之间的距离都小于dc。然后,在所有的高密度聚类中心点两两之间计算是否dc可达,如果可达则合并。
如图3,针对高密度点,如图3(b)中蓝色的点,对高密度点进行聚类,如图3(c),可以聚成4类,分别对这4类的中心点如图3(d),中心点合并后的效果如图3(e),最后低密度点聚类,如图3(f)。
3.4 算法流程
下面从4个方面来描述本文所提方法:算法主体、密度中心计算、数据点分配、密度中心合并。
算法1给出了本文算法的整体流程。
算法1算法主体
输入:待聚类数据集。
输出:每个数据点的聚类结果。
1.根据公式(1)计算截止距离dc。
2.根据公式(5)计算高低密度分界值。
3.调用算法2,对高密度点进行密度中心计算。
4.调用算法3,实现聚类中心合并。
5.调用算法4,实现数据点的分配。
算法2,是根据3.2节的分析而实现,属于密度二分法中的第一个关键步骤。
算法2密度中心计算
输入:所有高密度数据点。
输出:聚类中心点的编号。
1.使用公式(3),重新计算高密度点的ρi。
2.使用公式(6),计算 δi。
3.使用公式(8),计算聚类中心点。
算法3,可以有效避免,同一个类中,由于存在多个密度峰值点,而被误判为多个类。
算法3聚类中心合并
输入:所有聚类中心点的编号。
输出:新的聚类中心。
1.计算聚类中心点两两之间,是否dc可达。
2.如果两个点之间dc可达,把两者中密度较小点从集合C中删除。
算法4,是根据3.3节的分析而实现。
算法4数据点分配
输入:所有数据点和聚类中心。

图3 高密度点和低密度点计算示意图
输出:所有点的归类。
1.对于高密度点使用与原密度峰值聚类方法算法同样的策略。
2.对于低密度点做如下操作
2.1首先通过以下公式定义点i和 j之间的相似度wij。
2.2定义类归属的概率,点i到点c的概率。
2.3对进行排序升序排序,点i归属到比它大一些的那个点 j。
3.5 算法复杂度分析
本文所提算法主要有4个部分组成:算法1中的dc的计算,算法2中的密度和距离的计算,算法3中的dc可达性计算,算法4中的类归属概率的排序。下面就从这4部分对算法的时间复杂度进行分析。
假设样本数为N,需要计算所有点对之间的截止距离dc,计算复杂度为O(N2)。
接下来算法的其余3部分的计算复杂度从最好情况、最坏情况、平均情况这3类进行分析。
在最好的情况下,高密度点只有m个,其中m≪N,则计算密度和距离的复杂度为O(m2),且O(m2)≪O(N2)。每个聚类中心搜索路径的计算复杂度为O(m2),dc可达性计算的计算复杂度为其中mc为聚类中心的数目,类归属概率的排序的计算复杂度为O( )NlogN 。通过计算,本文所提算法整体上计算复杂度为O(N2)。
最坏的情况下,高密度点有N-1,则密度和距离的计算复杂度为O((N-1)2);对于每个聚类中心搜索路径的计算复杂度为O((N-2)2),dc可达性计算复杂度由于不存在低密度点,因此没有必要对算法4中的类归属概率进行排序。所以整体上计算复杂度为O(mcN2)。
平均情况下,高密度点有mh,则低密度点有N-mh,密度和距离的计算复杂度为O((mh)2);对于每个聚类中心搜索路径的计算复杂度为O((mh-1)2),dc可达性的计算复杂度为类归属概率的排序计算复杂度为由数学归纳法可证明,算法整体计算复杂度为O(N2logN)。
通过分析,可以看出,在所有类间距足够大且每类高密度点只有一个的情况下,算法时间复杂度将达到最优;在类与类之间边界交叉较多且类中包含多个高密度点的情况下,成为最坏时间复杂度。这两种情况都属于比较少见的情况。大部分情况下,趋近于平均时间复杂度O(N2logN)。
4 实验与分析
本章在合成的和真实的数据集上完成了一系列实验,将基于数据点密度二分法的密度峰值聚类方法(以下简称 DD-DPC)与 DPC[1]、ADPC-KNN[17]、DNDPC[18]等算法作了分析和对比。采用了聚类算法常用的对比指标调整后的兰特指数(ARI),每个基准值的范围从0到1,值越大,表示聚类效果越好。
为了比较候选聚类算法的优点,在实验中使用的数据列于表1。包括9个来自东芬兰大学1http://cs.joensuu.fi/sipu/datasets/的shape数据集。表1总结了所有数据集的属性数量和类数。
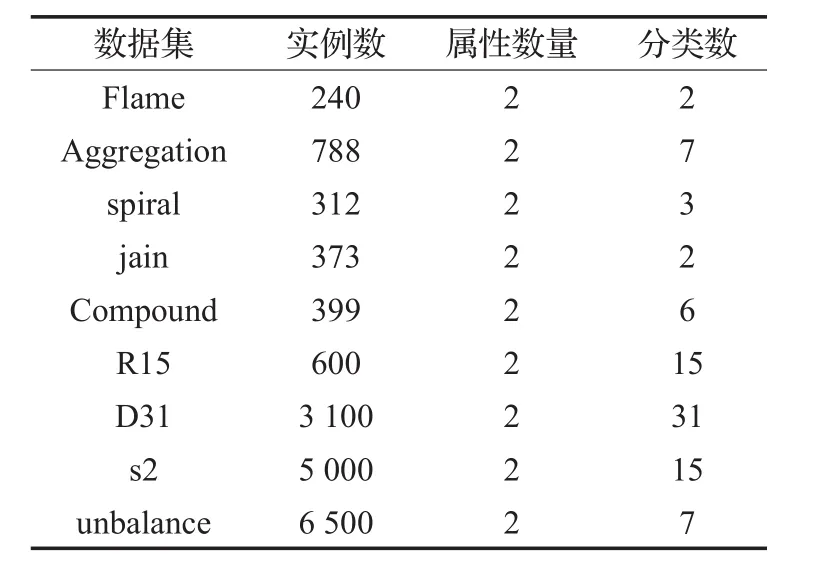
表1 9个实验数据集的信息
4种聚类算法都需要设置多种参数。DD-DPC和ADPC-KNN只需要一个参数即k近邻点个数,可预先指定。DPC和DNDPC都需要设置截止距离dc,初始聚类中心,由密度ρ和距离δ决策图手动选择。对于4种聚类算法在每个数据集上执行了多次,列出了每个方法的最佳结果。实验中4种聚类算法的参数都是精心挑选的。
4.1 聚类结果分析
将对DD-DPC、DPC、ADPC-KNN、DNDPC这4种算法在3种典型的二维数据集(Aggregation、Jain、Compound)上进行聚类分析比较。每个图像分别显示4种算法的聚类结果,使用不同的颜色和形状代表不同的聚类,如图4~6所示,其中子图(a)表示数据的真实结果,图(b)表示新算法的聚类结果,(c)~(e)子图分别表示DPC、ADPC-KNN、DNDPC算法的聚类结果。每个聚类中心每个聚类中心分别使用菱形方块表示。
图4中的Aggregation数据集,它有7个不同大小和形状的类,两对聚类相互连接。DD-DPC和DNDPC都可以找到正确的聚类中心和聚类,并获得与数据几乎一致的聚类结果,这个从4.2节的指标比较中也能看出。而DPC聚类算法由于无法处理类中拥有两个高密度点的情况,导致左下角的大类被分割成两类;ADPC-KNN由于计算出来的dc过大,导致左下角3个类都被误分为同一类。在表2中,DD-DPC和DNDPC的ARI都是将近100%准确,而DPC和ADPC-KNN则相对正确率低很多。
图5中的Jain数据集,它有2类373点构成,每个类中密度相对均匀,每个类都有多个高密度的点,在聚类中心决策图上可能会被认为聚类中心,导致聚类成多个类。图5分别显示了聚类中心和聚类效果。DD-DPC通过去除低密度点和合并聚类中心点可以获得良好效果。而DPC,DNDPC则会认为多个高密度点都是聚类中心,导致聚类成多个类。ADPC-KNN虽然能够合并,但是由于下方类的上半部分与上方类相对较近,导致聚类错误。
对于图6中的Compound数据集,它有399个点6类不同形状的聚类,点分布不均匀,其中有的类被另外一个类包含在中间。DD-DPC能够识别出包含在中间的类,但是识别不出分别在右边的那个密度相对小得多的类。而DPC、ADPC-KNN和DNDPC在对包含在里面的类无能为力。

图4 Aggregation数据集

图5 Jain数据集
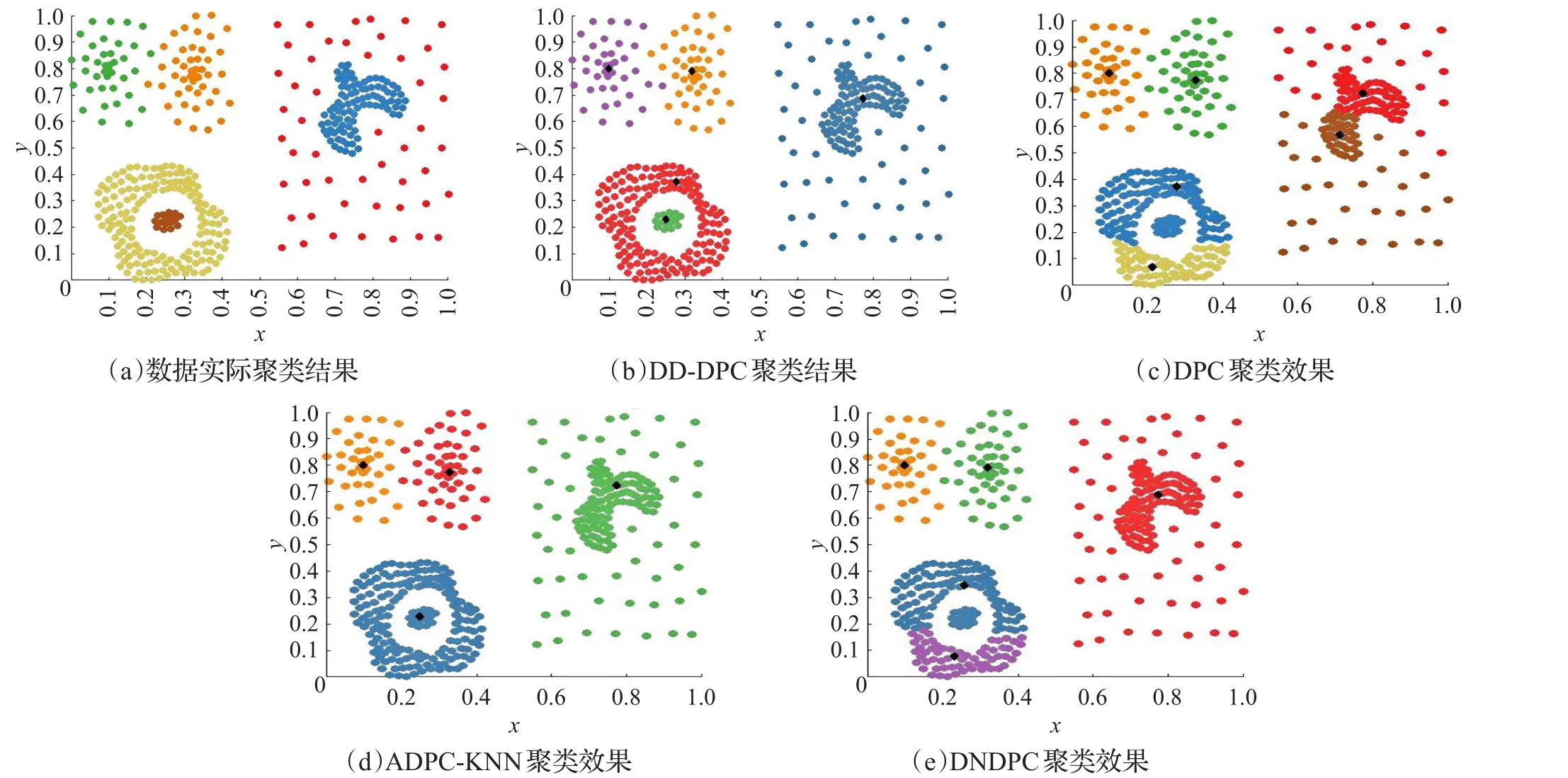
图6 Compound数据集
4.2 算法指标对比与分析
本节分别对4种算法,对调整后的兰特指数(ARI)指标进行比较。每个基准值的范围从0到1,值越大聚类效果越好。粗体表示结果最好。
表2表明,DD-DPC算法在unbalance数据集上表现略逊色于NDDPC,即说明也能处理类密度分布不均衡的情况。但是在其他数据集上,本文提出的DD-DPC在数据集上的表现良好,特别是Jain和Compound数据集上。因为该数据集中包含多个高密度峰值。
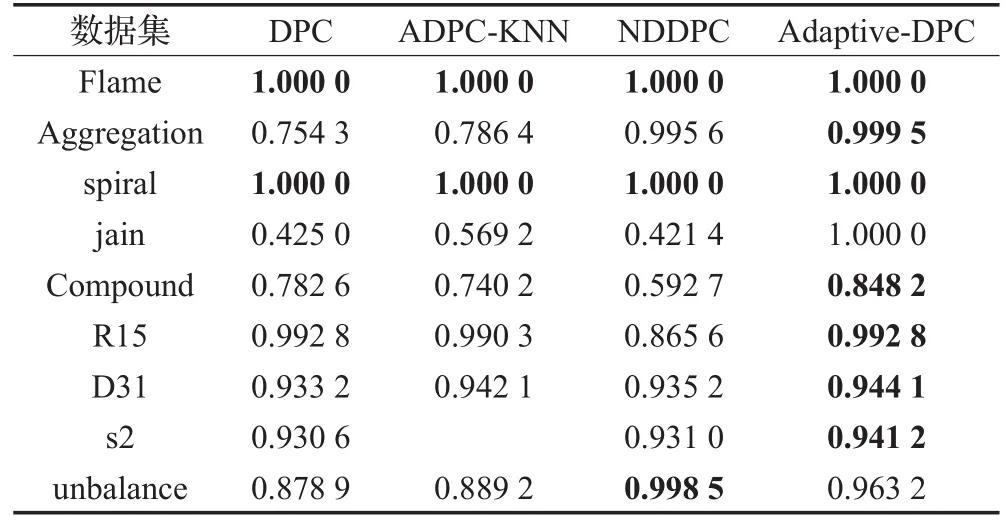
表2 4种聚类算法在合成数据集上的ARI指标比较
5 结论
本文的核心工作在于将密度峰值聚类方法的聚类过程视为聚类中心确定、每个数据点的聚类归属两个环节,然后提出将数据按照密度分为高密度和低密度分别聚类,提出了基于数据点密度二分法的密度峰值聚类方法。
在多个合成及实际数据集上,从聚类可视化结果以及调整后的兰特指数(ARI)指标上进行比较,实验结果表明,本文所提方法,能够有效地处理聚类中心的数据点密度差异较大,或者同一个聚类中包含多个密度中心等情况下,密度峰值聚类方法聚类效果受到影响的问题。
[1]Rodriguez A,Laio A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.
[2]Wang Y,Chen Q,Kang C,et al.Clustering of electricity consumption behavior dynamics toward big data applications[J].IEEE Transactions on Smart Grid,2016,7(5):2437-2447.
[3]Liu P,Liu Y,Hou X,et al.A text clustering algorithm based on find of density peaks[C]//2015 7th International Conference on Information Technology in Medicine and Education(ITME),2015:348-352.
[4]Yu J,Xie L,Xiao X,et al.A density peak clustering approach to unsupervised acoustic subword units discovery[C]//2015 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference(APSIPA),2015:178-183.
[5]Qin Y,Zhao C,Gao F.An iterative two-step sequential phase partition(ITSPP) method for batch process modeling and online monitoring[J].AIChE Journal,2016,62(7):2358-2373.
[6]Li S,Zhou X,Shi H,et al.An efficient clustering method for medical data applications[C]//2015 IEEE International Conference on Cyber Technology in Automation,Control,and Intelligent Systems(CYBER),2015:133-138.
[7]Liu Dongchang,Cheng S F,Yang Yiping.Density peaks clustering approach for discovering demand hot spots in city-scale taxi fleet dataset[C]//2015 IEEE 18th International Conference on Intelligent Transportation Systems,2015:1831-1836.
[8]Du H.Robust local outlier detection[C]//2015 IEEE International Conference on Data Mining Workshop(ICDMW),2015:116-123.
[9]Jia S,Tang G,Hu J.Band selection of hyperspectral imagery using a weighted fast density peak-based clustering approach[C]//International Conference on Intelligent Science and Big Data Engineering,2015:50-59.
[10]Ma C,Ma T,Shan H.A new important-place identification method[C]//2015 IEEE International Conference on Computer and Communications(ICCC),2015:151-155.
[11]Mehmood R,Bie R,Dawood H,et al.Fuzzy clustering by fast search and find of density peaks[C]//2015 International Conference on Identification,Information,and Knowledge in the Internet of Things(IIKI),2015:258-261.
[12]Wang X F,Xu Y.Fast clustering using adaptive density peak detection[J].Statistical Methods in Medical Research,2015,26(6):2800-2811.
[13]Wang S,Wang D,Li C,et al.Clustering by fast search and find of density peaks with data field[J].Chinese Journal of Electronics,2016,25(3):397-402.
[14]Mehmood R,Zhang G,Bie R,et al.Clustering by fast search and find of density peaks via heat diffusion[J].Neurocomputing,2016,208:210-217.
[15]Yan Z,Luo W,Bu C,et al.Clustering spatial data by the neighbors intersection and the density difference[C]//2016 IEEE/ACM 3rd International Conference on Big Data Computing Applications and Technologies(BDCAT),2016:217-226.
[16]Du M,Ding S,Jia H.Study on density peaks clustering based on k-nearest neighbors and principal component analysis[J].Knowledge-Based Systems,2016,99:135-145.
[17]高诗莹,周晓锋,李帅.基于密度比例的密度峰值聚类算法[J].计算机工程与应用,2017,53(16):10-17.
[18]李建勋,申静静,李维乾,等.基于趋势函数的空间数据聚类方法[J].计算机工程与应用,2017,53(6):22-28.
[19]Liu Y,Ma Z,Yu F.Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J].Knowledge-Based Systems,2017,133.
[20]Hou J,Cui H.Density Normalization in density peak based clustering[C]//International Workshop on Graphbased Representations in Pattern Recognition,2017:187-196.
[21]Barany I,Vu V H.Central limit theorems for Gaussian polytopes[J].Annals of Probability,2006,35(4):1593-1621.
