基于犹豫语言决策模型的数据产品服务商选择
2018-06-26戴意瑜
戴意瑜
华侨大学 网络与教育技术中心,福建 厦门 361021
1 引言
数据产品服务商是数据产品的供给方,它是根据用户的命令对数据执行必要的操作。数据产品管理中一个非常重要的问题就是数据产品服务商的选择问题,而数据产品服务商的选择问题本质上是一种模糊多属性群决策问题。模糊集[1]能够合理和便捷地处理模糊和不确定信息,随后各种模糊集的诱导形式相继被提出,包括直觉模糊集[2]、犹豫模糊集[3]、毕达哥拉斯模糊集[4]、犹豫正态模糊集[5]、二型模糊集[6]等等。然而语言信息能够贴近于人类的认知,所以运用语言变量表达决策者评估信息更为合理和直观。因此,Zadeh[7]于1975年提出了模糊语言方法。为了保持语言决策信息的全面性,Rodríguez等[8]引入了犹豫模糊语言术语集(HFLTS)的概念。Liao等[9]用数学的方法重新定义了HFLTS。
模糊理论中一个重要研究课题就是模糊决策方法的设计。文献[10]首次运用线性分配方法解决多属性决策问题。Borovička[11]考虑属性间的差异提出了改进的模糊分配方法。Chen[12]针对区间二型梯形模糊数,建立了新的线性分配方法用以确定最优方案排序。文献[13]基于直觉正态模糊信息集成算子,构建了新的多属性决策模型。文献[14]设计了基于最大群体效用与最小个体遗憾两个目标的群体信息集结优化模型。陈秀明和刘业政[15]提出多粒度犹豫模糊语言环境下未知权重的多属性群推荐方法。Liao等[16]建立了一种HFL-VIKOR方法用以处理属性间存在冲突的决策问题。Wei等[17]基于HFLTS得分函数提出了新的犹豫模糊语言TODIM方法。文献[18]建立了新的对犹豫模糊语言元进行完全排序的关系系统。Chen[19]研究了一种基于区间type-2模糊集的似然分配方法,并将其应用于备选方案的排序/选择问题。在犹豫模糊信息环境下,文献[20]依据属性重要性和欧几里德距离,设计一种线性分配方法确定备选方案的最优偏好排序。
综上可知,犹豫模糊语言信息理论是一个重要的研究课题。因此,有必要对犹豫模糊语言线性分配模型方法进行研究。本文首先提出犹豫模糊语言元间的可能度和差异度概念,然后设计犹豫模糊语言元最优度公式,最后建立犹豫模糊语言线性分配算法,并通过数据产品服务商选择实例说明本文方法的有效性。
2 基础知识
假设 S={st|t=-τ,…,-1,0,1,…,τ}为一个下标对称的语言集,其中s0表示无差别的语言变量,τ为一个正整数。为了方便起见,记M={1,2,…,m},N={1,2,…,n}。
定义1[9]令xi∈X(i∈N)为一个给定的集合,则定义在X上的犹豫模糊语言集(HFLS)表示为B={
定义2[12]令a=[a-,a+]和b=[b-,b+]为两个区间数,L(a)=a+-a-,L(b)=b+-b-,则称:
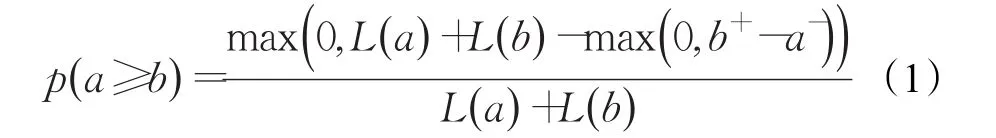
为a≥b的可能度。
3 基于犹豫模糊语言可能度的线性分配模型
主要针对犹豫模糊语言多属性决策问题,运用犹豫模糊语言可能度,构建新的线性分配方法处理决策问题。
令A={A1,A2,…,Am}为一个备选方案矩阵,C={C1,C2,…,Cm}是一组属性指标,其权重向量为w=(w1,w2,…,wn)T,备选方案Ai在属性指标Cj下的评估信息用HFLEhij表示,于是得到一个犹豫模糊语言决策矩阵H=(hij)m×n。
3.1 犹豫模糊语言可能度
在引入犹豫模糊语言可能度之前,首先提出HFLE的包络概念。
定义3令h是一个HFLE,则称语言变量区间env(h)=[h-,h+]为h的包络,其中

定义4假设h1和h2为两个HFLE,它们的包络分别为 env(h1)=[sα-,sα+]和 env(h2)=[sβ-,sβ+]。令 L(env(h1))=则称:
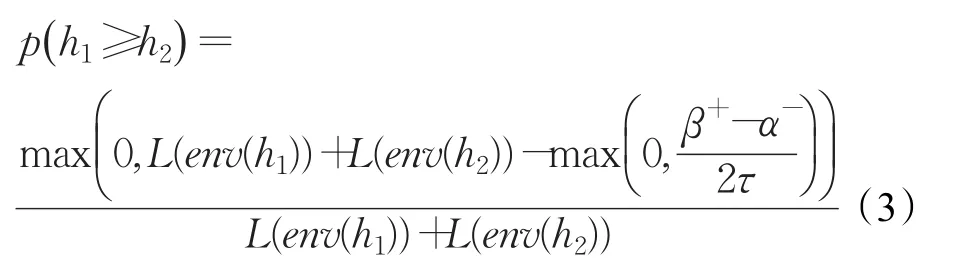
为h1≥h2的可能度。
于是,基于犹豫模糊语言决策矩阵H,运用公式(3)可以计算每个属性Cj下的可能度 p(hij≥hkj),从而得到n个可能度矩阵:
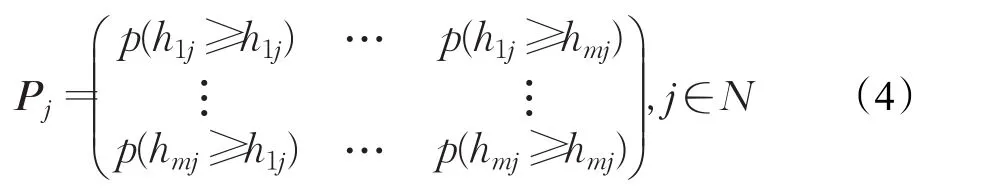
定理1 令h1和h2为两个HFLE,则可能度 p(hij≥hkj)满足以下性质:
(1)0≤p(hij≥hkj)≤1。
(2)p(hij≥hkj)+p(hkj≥hij)=1 。
(3)如果 p(hij≥hkj)=p(hkj≥hij),则有 p(hij≥hkj)=p(hkj≥hij)=0.5。
(4)p(hij≥hij)=0.5 。
由于定理1的证明过程简单,在此省略。
定理2假设可能度矩阵Pj中的所有元素 p(hij≥hkj)(i,k∈M)是由公式(3)计算得出,那么矩阵 Pj是一个互补判断矩阵。
证明 对于任意一个属性Cj,根据定理1的性质(1)和性质(2)可得,0≤p(hij≥hkj)≤1且 p(hij≥hkj)+p(hkj≥hij)=1,∀i,k∈M ,即可能度矩阵Pj中的所有元素满足互补判断矩阵的条件。因此Pj是一个互补判断矩阵。
3.2 犹豫模糊语言线性分配模型
令 p(hij≥hkj)(k∈M)和 p(hlj≥hkj)(k∈M)分别为互补判断矩阵 Pj的第i行和第l行可能度元素,那么HFLEhij和hlj间的相对差异指数φjil计算如下:

于是在属性指标Cj下HFLEhij和hlj间的所有相对差异指数(i,l∈M)构成一个相对差异矩阵:

定理3令ψj是一个相对差异矩阵,其中的元素是由公式(5)计算得到,那么ψj是一个互补判断矩阵。
证明(1)根据定理1有0≤p(hij≥hkj)≤1且 p(hij≥hij)=0.5,所以对 ∀i,l∈M ,有:
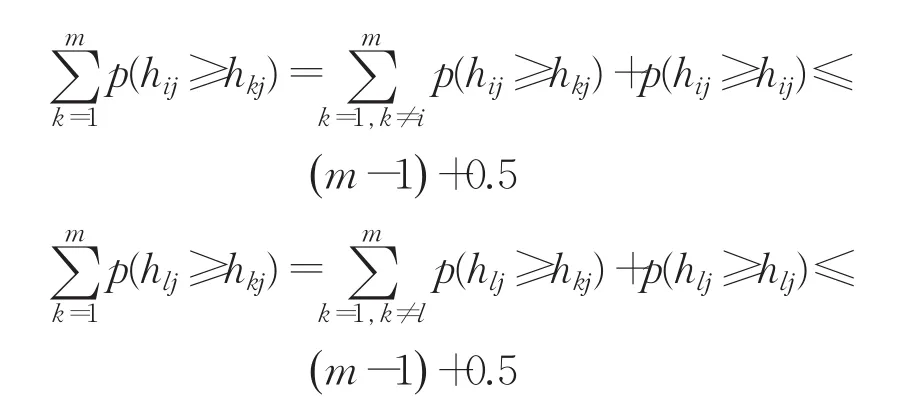
从而

用公式(6)减去公式(7),可得:

而m≥1,因此:

则有:

即0≤≤1,(i,l∈M)。
(2)又因为对 ∀i,l∈M ,有:
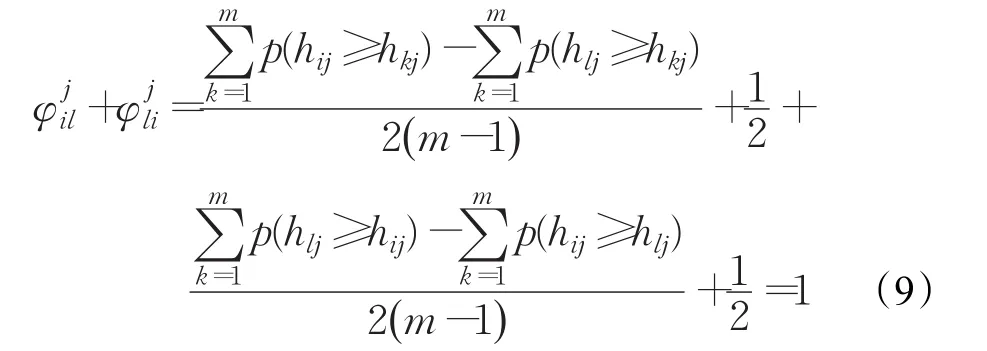
综上,ψj是一个互补判断矩阵。定理2得证。
根据相对差异指数,引入如下定义。
定义5令hij是犹豫模糊语言决策矩阵中备选方案Ai相对于Cj的评估信息值,则称

为hij的最优度,其中

表示相对差异矩阵ψj的第i行元素的相加值。
定理4设hij是犹豫模糊语言决策矩阵中备选方案Ai相对于Cj的评估信息值,则有:
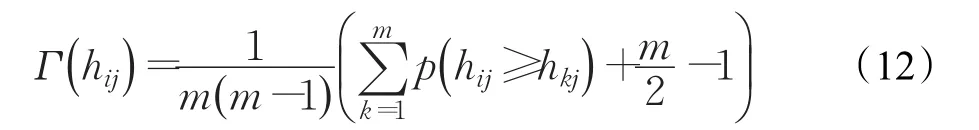
证明 将公式(11)代入公式(10)可得:

根据定理2和定理3可知,矩阵Pj和ψj均为互补判断矩阵,则有:

所以

于是结论成立。
基于上述分析过程,建立如下犹豫模糊语言线性分配算法,用以选择出性能最优的备选方案,详细步骤如下:
步骤1决策者构建犹豫模糊语言决策矩阵H=(hij)m×n,并给出属性集合C={C1,C2,…,Cm}对应的权重向量为w=(w1,w2,…,wn)T。
步骤2利用定义3和公式(3)分别计算每个HFLEhij的包络和hij≥hkj的可能度 p(hij≥hkj)(i,k∈M),于是得到属性Cj(j ∈N )对应的互补判断矩阵Pj(j ∈N )。
步骤3运用公式(5)计算相对差异指数M),并构造相对差异矩阵ψj(j ∈N )。
步骤4 依据公式(10)和(11),确定 hij的最优度Γ(hij)(i∈M,j∈N)。
步骤5基于属性权重w=(w1,w2,…,wn)T,利用公式(14)计算备选方案Ai的加权最优度Γ(hi):
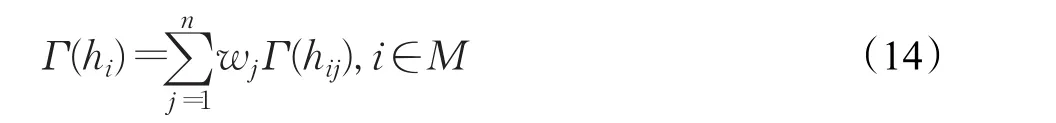
步骤6根据加权最优度Γ(hi)(i∈M)的大小对备选方案Ai(i∈M)进行优劣排序。Γ(hi)越大,则对应的备选方案越优。
4 案例分析
某一移动通信公司为了改善用户的服务体验,增加通信用户占有率,欲在第三方市场中选择一家数据产品服务商。现已筛选出四家较为合适的数据产品服务商分别为{A1,A2,A3,A4},在筛选最优数据产品服务商时,主要参考四个评估指标:产品质量(C1)、处理能力(C2)、存储性能(C3)、售后服务(C4)进行评估,且这四个属性指标的权重向量为w=(0.15,0.3,0.2,0.35)T。专家们依据自身的专业知识和经验技能,评估得到每家数据产品服务商的属性值HFLEhij={γij∈S={s-3,s-2,…,s3}},进而得到了表1所示的犹豫模糊语言决策矩阵H=(hij)4×4。运用犹豫模糊语言线性分配算法处理上述问题,详细过程如下。

表1 犹豫模糊语言决策矩阵
步骤1计算犹豫模糊语言决策矩阵H=(hij)4×4,结果如表2所示。

表2 犹豫模糊语言决策矩阵的包络
步骤2计算四种属性指标对应的互补判断矩阵Pj(j=1,2,3,4 ):

步骤3运用公式(5)计算相对差异矩阵ψj(j=1,2,3,4):
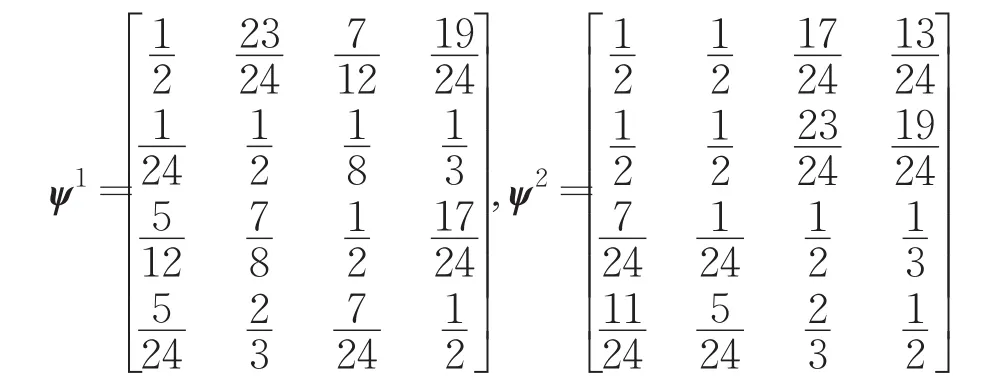

步骤4 依据公式(10)和(11),得到表3所示的最优度矩阵。
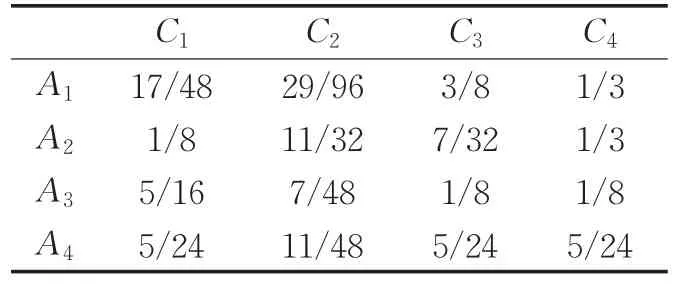
表3 最优度矩阵
步骤5利用公式(14)计算四家数据产品服务商的加权最优度分别为:

步骤6 因为 Γ(h1)>Γ(h2)>Γ(h4)>Γ(h3),所以四家数据产品服务商的优劣排序为A1≻A2≻A4≻A3,即综合表现最高的数据产品服务商为A1。
为了说明本文方法的有效性,接下来运用文献[21]中的TOPSIS方法处理上述问题,大致步骤如下。
首先计算决策矩阵的包络同本文方法一致,然后设计正负理想点如下:
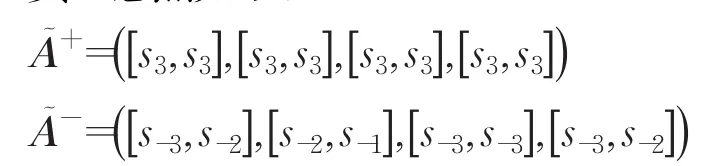
其次,根据文献[19]中的距离公式计算四家数据产品服务商距离正负理想点的距离为:
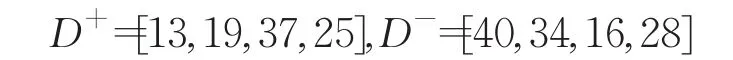
最后,分别计算四家数据产品服务商的相对贴近度为:

从而根据贴近度的大小对数据产品服务商的排序为A1≻A2≻A4≻A3,因此最理想的数据产品服务商也为A1。
根据决策结果可知,运用两种方法得到的决策结果一致,这说明本文方法是合理有效的。相比之下,本文方法将犹豫模糊语言信息通过包络方法转化为区间形式,是一种新的处理犹豫模糊语言信息的方法,同时,本文方法将整体的决策信息拆解为各属性下的信息进行分析,能够更为深刻地挖掘原始决策信息,从而使得决策结果更为合理可靠。
5 结束语
本文主要建立了一种犹豫模糊语言线性分配模型用以处理多属性决策问题。首先,基于犹豫模糊语言元的包络概念,提出了犹豫模糊语言元间的可能度和相对差异指数等定义,并得出它们构成的矩阵均为互补判断矩阵。然后,设计了犹豫模糊语言元的最优度计算公式。最后建立了一种新的犹豫模糊语言多属性决策方法,即犹豫模糊语言线性分配算法,并通过数据产品服务商选择实例说明本文方法的可行性和有效性。在本文研究的基础上,在区间犹豫模糊语言信息环境西下,将考虑决策者态度参数的连续有序加权算子引入到可能度和相对差异指数的构造和分析过程中,并将构建的决策方法应用于诸如模式识别、医疗诊断等其他领域,可以做进一步深入的研究。
[1]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-356.
[2]Atanassov K T.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.
[3]Torra V.Hesitant fuzzy sets[J].International Journal of Intelligent Systems,2010,25:529-539.
[4]Yager R R,Abbasov A M.Pythagorean membership grades,complex numbers,and decision making[J].International Journal of Intelligent Systems,2013,28(5):436-452.
[5]马庆功.广义犹豫正态模糊信息集成及其多属性群决策[J].计算机工程与应用,2015,51(22):134-140.
[6]Zhai D,Mendel J M.Uncertainty measures for general Type-2 fuzzy sets[J].Information Sciences,2011,181(3):503-518.
[7]Zadeh L A.The concept of a linguistic variable and its application to approximate reasoning[J].Information Sciences,1975,8(2):99-249.
[8]Rodríguez R M,Martínez L,Herrera F.Hesitant fuzzy linguistic terms sets for decision making[J].IEEE Transactions on Fuzzy Systems,2012,20:109-119.
[9]Liao H C,Xu Z S,Zeng X J,et al.Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets[J].Knowledge-Based Systems,2015,76:127-138.
[10]Bernardo J J,Blin J M.A programming model of consumer choice among multi-attributed brands[J].Journal of Consumer Research,1977,4(2):111-118.
[11]Borovička A.Possible modifications of the multiple criteria assignment method[J].Auco Czech Economic Review,2013,7(1):55-67.
[12]Chen T Y.A linear assignment method for multiplecriteria decision analysis with interval type-2 fuzzy sets[J].Applied Soft Computing,2013,13(5):2735-2748.
[13]时恩早,范颖.基于直觉正态模糊信息集成的多属性决策[J].控制工程,2016,23(10):1612-1617.
[14]杨欣蓉,钱钢,冯向前.基于犹豫模糊语言多属性群决策的VIKOR扩展方法[J].计算机工程与应用,2017,53(11):39-43.
[15]陈秀明,刘业政.多粒度犹豫模糊语言环境下未知权重的多属性群推荐方法[J].控制与决策,2016,31(9):1631-1637.
[16]Liao H C,Xu Z S,Zeng X J.Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making[J].IEEE Transactions on Fuzzy Systems,2015,23(5):1343-1355.
[17]Wei C P,Ren Z L,Rodriguez R M.A hesitant fuzzy linguistic TODIM method based on a score function[J].International Journal of Computational Intelligence Systems,2015,8(4):701-712.
[18]Wang J Q,Wang J,Chen Q H,et al.An outranking approach for multi-criteria decision-making with hesitant fuzzy linguistic term sets[J].Information Sciences,2014,280:338-351.
[19]Chen T Y.A likelihood-based assignment method for multiple criteria decision analysis with interval type-2 fuzzy information[J].Neural Computing&Applications,2016:1-23.
[20]Wei G,Alsaadi F E,Hayat T,et al.A linear assignment method for multiple criteria decision analysis with hesitant fuzzy sets based on fuzzy measure[J].International Journal of Fuzzy Systems,2016,19(3):1-8.
[21]Beg I,Rashid T.TOPSIS for hesitant fuzzy linguistic term sets[J].International Journal of Intelligent Systems,2013,28:1162-1171.
