求解高维复杂优化问题的改进人工蜂群算法

贺桂娇 ，周树亮 ，冯冬青

1.广州现代信息工程职业技术学院，广州 510663

2.郑州大学 电气工程学院，郑州 450001

3.中国中铁工程装备集团有限公司，郑州 450016

1 引言

Artificial Bee Colony（ABC[1]）算法是2005年由土耳其学者Karaboga提出的一种新的群体智能算法。ABC算法因原理简单、控制参数少、灵活性及适应度高等特点[2]，越来越受到学者们的青睐。ABC算法常用于解决函数离散优化[3-4]和无约束优化问题[5]，但是ABC算法存在容易早熟收敛、收敛精度低、易陷入局部最优、后期跳出局部最优能力不足等缺点。究其原因都是因为ABC算法的开发能力不足。

针对上述问题，研究者提出了很多改进方案。暴励[6]等人在ABC算法中融合差分进化算法，提出BDABC算法，两种算法互相融合，共享最优解，收敛速度提高。汪继文[7]等人改进搜索方程，提出了ABC/current-to-best算法，收敛速度提高但是容易陷入局部最优。张泰[8]等人引入自适应步长策略，提出SAABC算法。Lv[9]等在全局搜索方程中加入高斯扰动，提出GBABC算法，算法的鲁棒性提高但是收敛精度改善甚微。Sharma[10]等在搜索方程中加入所有个体的位置信息，有效防止了算法陷入局部最优。Pan[11]等在搜索方程中加入全局最优解和一些随机个体，提高了算法的收敛精度，但是对于多模态复杂问题，寻优效果并没有多大改善。李国亮[12]研究ABC算法在不同的迭代阶段设计了不同的搜索方式，从而减低了算法陷入局部极值的可能性。Amira[13]结合量子计算和ABC算法，提出量子人工蜂群（QABC）算法，不仅提高算法的多样性，而且提高了计算能力。Zhang和Liu[14]结合DE算法改进蜂群算法，提出NABC算法，从而提高了算法的收敛精度。Sharma[15]设计了一种新颖的ABC算法DABC。DABC算法在两个方向上搜索潜在蜜源，有效提高了算法的收敛精度。

在标准ABC算法中，观察蜂按照轮盘赌策略选择蜜源。这种根据随机概率选择蜜源的方法，虽然保证了优秀的蜜源更容易被选中，但是选择失败经常发生。实验证明选择失败的次数大约为观察蜂个数的10倍。这无疑会耗费计算机资源，延长迭代时间。标准ABC采用轮盘赌选择策略，本质上为了保证适应度高的蜜源更容易被选中。在不违背这种初衷的情况下，BAABC算法不再通过轮盘赌选择蜜源，而是直接选择适应度高的蜜源。BAABC算法将吸引子引入到观察蜂的搜索方程中。种群中所有观察蜂围绕吸引子等比例收缩，集中开发一片区域，增加了局部开发能力。而且收缩是有方向意识的，在单峰函数求解过程中，方向正好是两点之间梯度方向，且方向为正。

仿真实验结果表明，BAABC算法的收敛速度和收敛精度都有很大的提高。更值得一提的是BAABC算法的收敛效果与问题维数无关。在解决高维复杂问题上，收敛效果明显优于其他算法，具有良好的鲁棒性。

2 标准人工蜂群算法

蜂群由雇佣蜂、跟随蜂和侦查蜂三部分组成。雇佣蜂（employed bee）处于特定的食物源，并且携带有关食物源的信息。跟随蜂（onlookers）通过雇佣蜂共享的信息寻找食物源。侦查蜂（scouts）负责在食物源附近搜索新的潜在食物源。

2.1 初始化

设蜂群大小为2×SN，目标函数 f(x)是一个D维的优化问题。蜜源代表了算法在搜索空间里随机生成的可行解，搜索空间内的可行解依照式（1）随机产生。

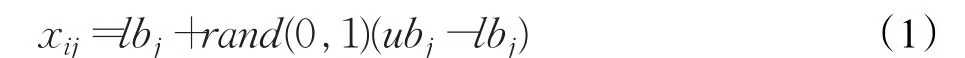
式中，j=1,2,…,D;i=1,2,…,SN,D为个体向量维数；lbj为第 j维下界；ubj为第 j维上界。

2.2 蜂群进化阶段

雇佣蜂在当前依附的蜜源附近进行邻域搜索，寻找更好的蜜源，如果发现比当前更优秀的蜜源，更新当前蜜源。雇佣蜂搜索方程式如式（2）所示：

式中，j=1,2,…,D;k=1,2,…,D;k是一个随机整数且k≠i;ϕij是在[-1,1]范围内的随机数。

跟随蜂根据雇佣蜂所携带的蜜源信息，按照轮盘赌选择策略进行依附，进而转化为雇佣蜂，并在蜜源邻域内搜索新的蜜源。跟随蜂依附后，按照式（2）进行搜索新蜜源。跟随蜂选择蜜源的方式采用轮盘赌方式，其选择概率如式（3）所示：

式中，fit(xi)是蜜源xi的适应度值；Pi是xi被选择的概率。

当雇佣蜂在迭代阈值limit范围内，未找到更好的蜜源，则雇佣蜂转变为侦查蜂，进行全局搜索，按照式（4）产生新解。

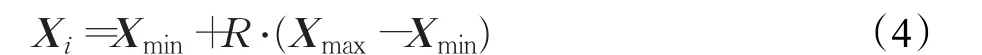
式中，向量Xmin=(lb1,lb2,…,lbD)；Xmax=(ub1,ub2,…,ubD)；R=(ϕ1,ϕ2,…,ϕD)；ϕ1,ϕ2,…,ϕD是在 [-1,1]范围内的随机数。

3 求解高维复杂优化问题的改进人工蜂群算法

在标准ABC算法中，观察蜂根据轮盘赌选择蜜源。轮盘赌虽然可以保证优秀蜜源更容易被选中，但是无法保证不出现选择失败。ABC算法通过迭代计算寻找最优解。若出现选择失败，那无疑会浪费一次迭代时间。这明显会浪费计算机资源。本文设计实验统计选择失败的次数。实验设置，种群大小20，迭代次数2 000次，运行10次。实验结果如表1所示。

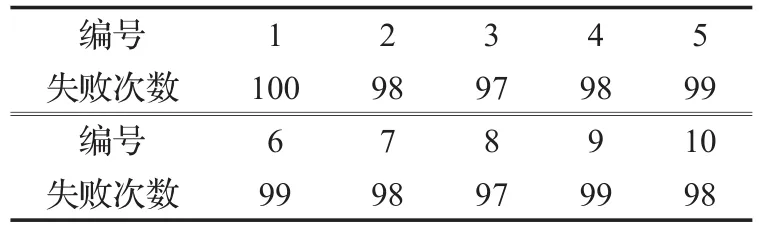
表1 观察蜂选择失败的次数

表1中数据是算法运行一次，在每次迭代中，观察蜂选择失败的次数。那么算法运行一次，观察蜂选择失败的次数是表中数据乘以2 000后的结果。可见，这个数目还是相当庞大的。根据表1得出，每次观察蜂选择失败的次数大约是100次。种群大小为20，那么观察蜂的个数为10。因此每次观察蜂搜索时，选择失败的次数大约是观察蜂个数的10倍。因此如果种群越大，选择失败的次数也就越多。进而，浪费的搜索时间也越多。

BAABC算法摒弃轮盘赌策略，并通过引进吸引子cr改变观察蜂的搜索方式。所有观察蜂都以吸引子为中心等比例收缩，共同开发同一区域，从而提高了算法的开发能力。吸引子cr作为蜂群中的“蜂王”，吸引所有观察蜂等比例靠近它，并共同开发“蜂王”所在的区域。BAABC算法的搜索示意图如图1所示。其中红色球代表吸引子cr，黑色球代表种群个体的当前位置，绿色球代表种群个体围绕吸引子cr收缩后的新位置，R为种群个体围绕吸引子收缩后的搜索空间半径。

图1 BAABC搜索示意图

BAABC算法分两种情况得到吸引子cr。当种群个体是全局最优解，吸引子cr根据式（5）得到，否则吸引子cr根据式（6）得到：

式中，vi是当前代表可行解的蜜源;r1、r2、r3是一组随机数且r1∈(0.5,1.5)，r2∈(-1,1)，r3∈(0,1)。 r1、r2、r3根据问题动态调整。如果测试函数局部最优点比较多，可以令r3∈(-1,1)。式（5）产生吸引子依赖于全局最优个体。式（6）中个体分量占主体，全局最有个体作为扰动分量。BAABC根据两种情况产生吸引子，较好地保留了种群的多样性，有效地避免了算法陷入局部最优解。在侦查蜂阶段，BAABC算法重新初始化未更新次数达到阈值的个体。这种方式进一步降低了算法陷入局部最优的可能性。

吸引子cr作为蜂群中心，每一个观察蜂都以它为中心，向它等比例收缩，既减少了个体飞出边界的可能，同时又增加了算法开发能力。收缩是有方向意识的，在单峰函数求解过程中，梯度在两点之间的分量正好为正，这说明两点之间任一可行解都会优于当前可行解，当然这是在吸引子优于当前可行解的情况下。在多峰函数求解过程中，由于局部峰值较多，难免会出现梯度在两点之间的分向量为负，但是这种收缩机制增强了局部开发能力，加快了后期的收敛速度和开采能力。对种群个体进行位置更新的公式，如式（7）所示：

式中，%是取模运算符；r=K×rand；K是大于零的整数；K的值决定了算法的缩放比例，所以对算法收敛精度有一定的影响，在本文第4章会分析K值大小对算法的影响;xmax，xmin分别是种群个体每一维的上界和下界。在算法每一代进化过程中，r的取值为定值。

本文中将雇佣蜂的搜索方程（2）改为式（8）：

式中，α是[0，1]之间的随机数；ϕij是[-1,1]之间的随机数；xg,j是全局最优解 j维。搜索方程加入全局最优解的引导，增强了算法的开发能力。

4 改进人工蜂群算法BAABC的流程步骤

步骤1设置种群规模2×SN，维数D，搜索区间等参数，按照式（1）随机生成代表可行解的初始蜜源。

步骤2雇佣蜂阶段：雇佣蜂按照式（8）进行蜜源邻域搜索新蜜源。计算适应度值，选择适应度好的蜜源。

步骤3观察蜂阶段：设定K值（每次迭代都是随机的），遍历种群中的每个观察蜂，根据式（5）和式（6）得到吸引子，根据式（7），所有观察蜂等比例向吸引子收缩。计算适应度值，选择适应度好的蜜源。

步骤4侦查蜂阶段：若存在放弃的蜜源，该处的雇佣蜂变为侦查蜂，根据式（4）产生新解。

步骤5判断是否满足循环终止条件，如果满足停止循环，输出结果，否则执行步骤2。

5 仿真实验和结果分析

为了验证改进算法的有效性，本文中选用了9个经典测试函数。

设计实验验证系数K对算法的影响。种群大小20，维数30，迭代次数2 000，实验结果如表2所示。

从表2中得出，K值影响算法收敛精度的大小。这是因为K值决定了算法的缩放比例，从而影响搜索空间。当K值比较大的时候，搜索空间的半径R就会过于小，致使算法很难跳出局部最优。如果搜索空间不对，那么无论多么努力，也找不到最优解。一般情况下，K取值不超过1.5。

为了进一步验证改进算法的效果，对比近年来几种改进ABC算法：ABCCTB算法[7]、基于交叉运算的全局人工蜂群算法CGABC[16]、基于边界改进的人工蜂群算法ABCMB和原始人工蜂群算法ABC分两组进行对比，第一组种群大小20，最大迭代次数1 000，维数100维，搜索范围(-30,30)，运行30次求平均值。两组实验结果见表3。第一组收敛曲线如图2所示。第二组种群大小20，最大迭代次数1 000，维数50维，搜索范围(-30,30)，运行30次求平均值。第二组收敛曲线如图3所示。

表2 K值对实验结果（平均值）的影响

表3 D=100,D=50,5种对比算法的实验结果

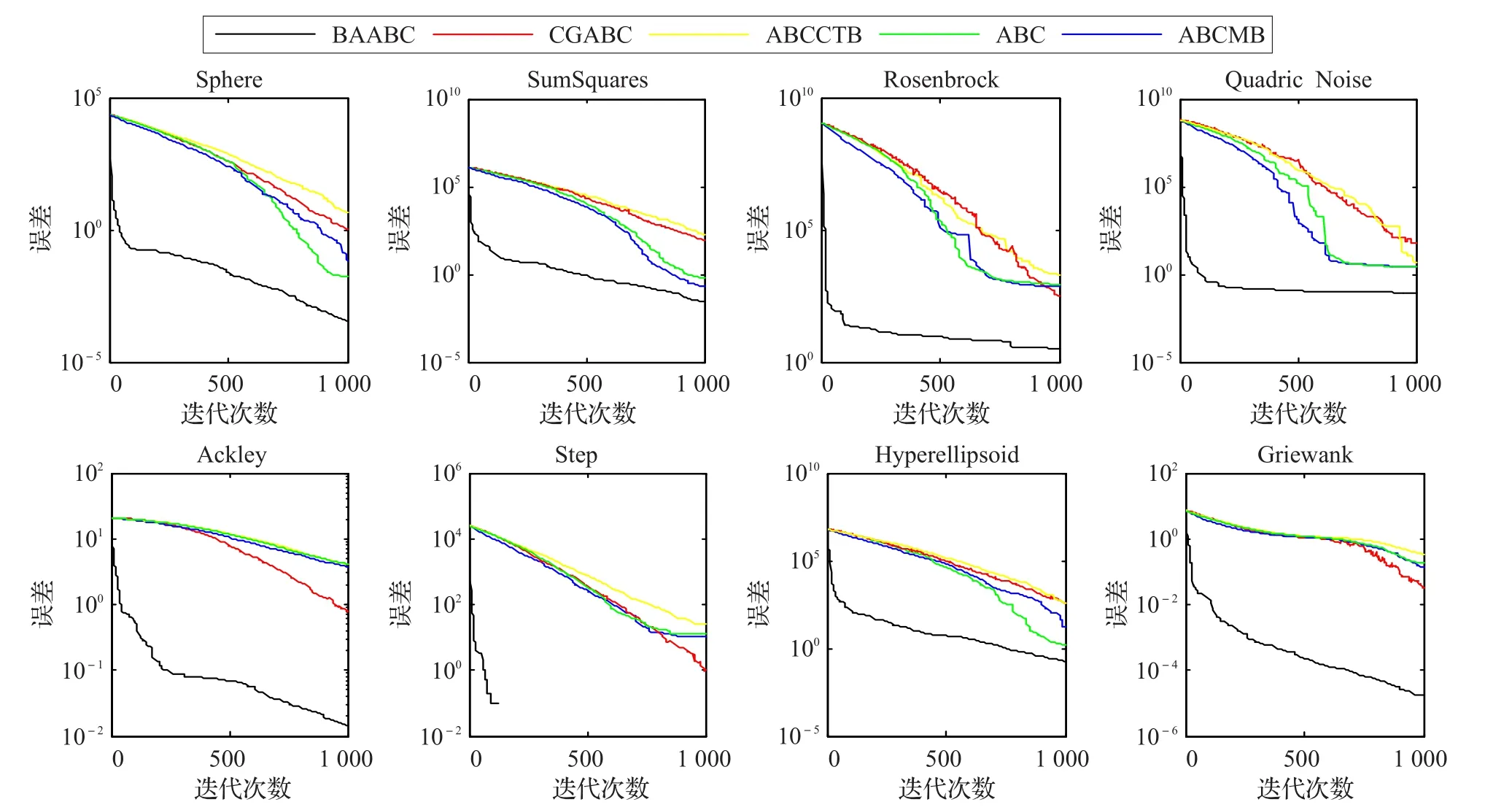
图2 D=100时，实验收敛曲线（关于迭代次数）

图3 D=50时，实验收敛曲线（关于迭代次数）

在BAABC算法中，观察蜂摒弃轮盘赌选择蜜源，而是采用围绕吸引子收缩更新蜜源。采用该方法可以省去选择失败的时间。为了验证BAABC算法关于时间的收敛速度。本文又设计了两组实验，第一组实验种群大小20，迭代时间6 s，问题维数50，运行30次；第二组实验种群大小20，迭代时间6 s，问题维数100，运行30次。实验目的就是，在有限收敛时间内，对比4种改进ABC算法和标准ABC算法的收敛效果。实验结果如图4所示。

本文选择的8个测试函数，涵盖单峰函数、多峰函数、复杂单峰函数。Sphere函数、SumSquares函数和Akely函数是收敛比较简单的单峰函数。这类测试函数主要是用来检验算法的收敛速度和全局搜索能力。Ronsenbrock函数虽然是一个单峰函数，但是很难找到它的全局最优解。这是因为在其最优解附近有一条平滑、狭长的抛物线形山谷，并且算法在这个山谷内很难辨别搜索方向。因此Ronsenbrock函数主要用来评价算法的开发能力和收敛精度。根据图2、3，从Sphere函数、SumSquares函数和Akely函数的收敛效果可以看出，BAABC算法的收敛速度是可圈可点的。从Ronsenbrock函数的收敛效果可以看出，BAABC算法的收敛精度和开发能力也是十分显著的。

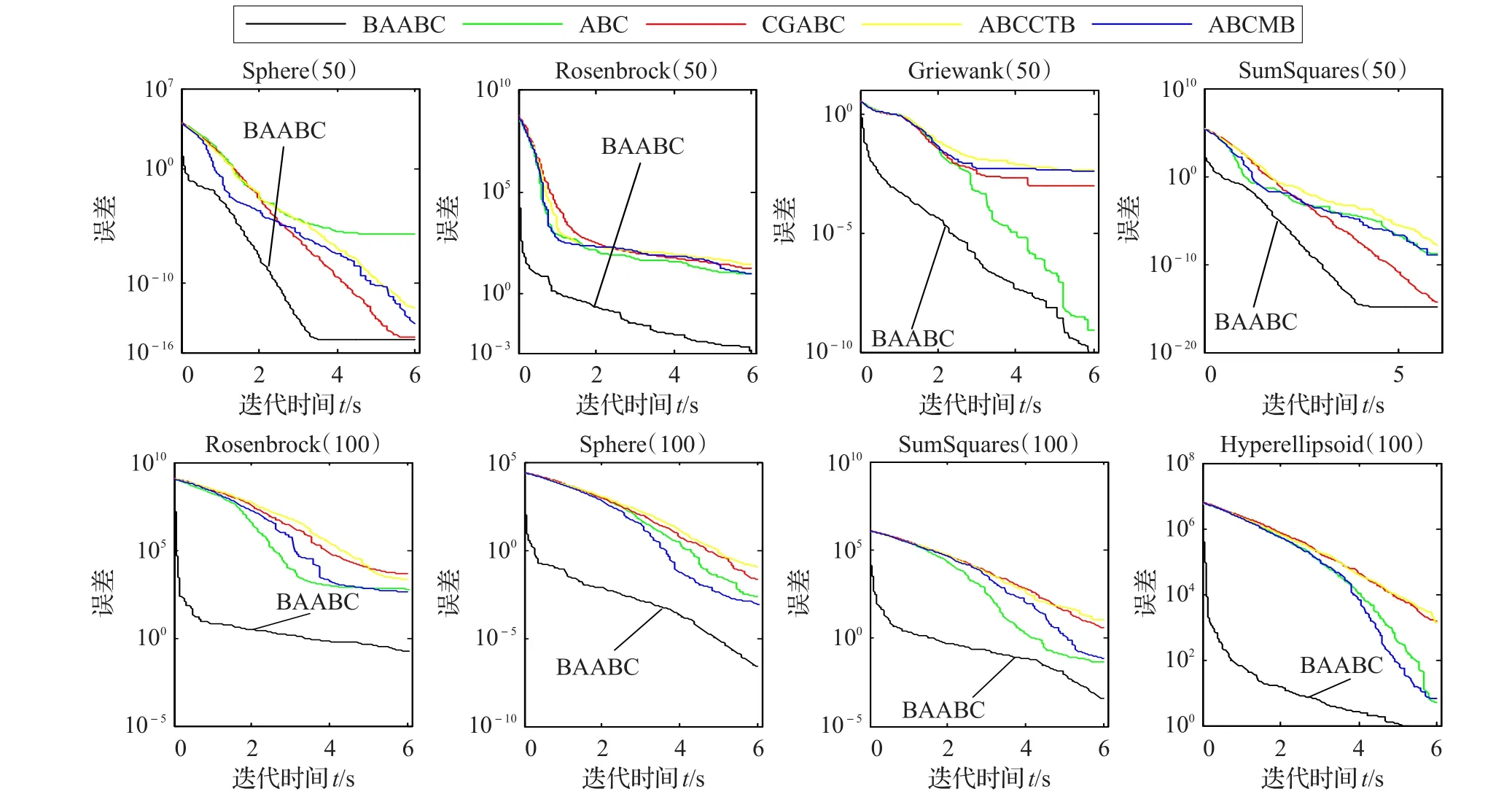
图4 D=50,100时，实验收敛曲线（关于迭代时间）

根据图4可得，BAABC算法无论在收敛速度还是在收敛精度上都优于其他算法，且其突出性能是收敛速度快。BAABC算法不仅关于迭代次数收敛速度快，而且关于迭代时间收敛速度快。BAABC算法是真正意义上的收敛速度快。

BAABC算法不同于标准ABC算法，摒弃轮盘赌方式，同时加强了鲁棒性。为了进一步测试BAABC算法的鲁棒性，本文设计了实验检验BAABC算法对高维复杂问题的优化效果，进行了两组实验，第一组设定维数200维，迭代次数1 000，搜索空间[-100,100]，运行50次，第二组设定维数300，500，…，1 000维，迭代次数2 000，搜索空间[-100,100]，运行50次，测试函数Rosenbrock、Ackley和Zakharov。运行结果和文献[13]中4种算法进行对比，数据来自于文献[13]。实验结果如表4所示，其中，MEAN代表均值；STD代表方差；OPT代表最优值；WST代表最差值。当维数为1 000维及2 000维时，BAABC算法的收敛性能如图5、6所示。

由表4可知，BAABC算法在解决高维复杂优化问题上，具有明显的优势，优化效果明显优于其他4种算法。当维数为200维时，BAABC算法收敛精度最高。当维数从300维到1 000维，对比BAABC算法的收敛效果，发现BAABC算法的收敛效果与问题维数无关，收敛精度基本上维持在10左右。从图5，6看出，即便在维数2 000维的时候，BAABC算法仍然可以得到不错的收敛精度。可见，BAABC算法具有非常好的鲁棒性，适合解决高维复杂优化问题，如无线传感器网络节点定位问题、无线Mesh网络QoS路由问题。

表4 5种算法和对比结果

图5 BAABC算法对Rosenbrock的收敛性能

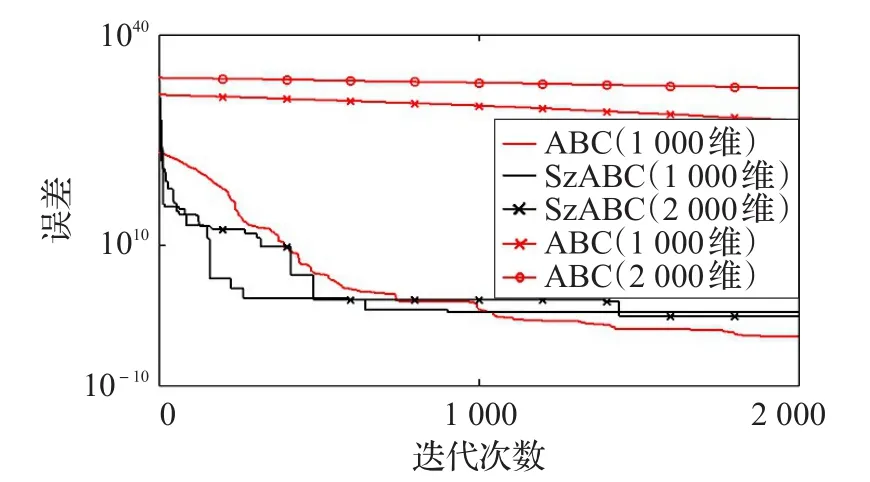
图6 BAABC算法对Zakharov的收敛性能

6 结论

在标准ABC算法中，观察蜂采用轮盘赌策略选择蜜源。但是这种方式会出现大量的选择失败，这无疑是浪费计算机资源的表现。鉴于标准ABC算法开发能力不足的情况，在观察蜂阶段，本文摒弃轮盘赌选择策略，改进观察蜂的搜索方式，以提高算法的开发能力。BAABC算法摒弃轮盘赌策略，并通过引进吸引子改变观察蜂的搜索方式。所有观察蜂以吸引子为中心等比例收缩，共同开发同一区域，从而提高了算法的开发能力。吸引子作为种群中心，所有观察蜂向吸引子靠拢，集中开发一片区域，提高算法的开发能力。通过实验证明，该方法明显提高了算法后期的局部开发能力。此外，在高维复杂优化问题上，BAABC算法的优化能力明显高于对比算法，具有良好的鲁棒性，适合在高维复杂优化问题上推广应用。

[1]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Turkey：Erciyes University，2005：1-10.

[2]Karaboga D，Basturk B.On the performance of artificial bee colony algorithm[J].Applied Soft Computing，2008，8（1）：687-697.

[3]李俊清，潘全科，王法涛.求解混合流水线调度问题的离散人工蜂群算法[J].运筹与管理，2015，24（1）：157-163.

[4]周逊，郭敏，马邈.一种求解图像分割问题的限速—离散蜂群优化算法[J].计算机工程，2014，40（8）：212-216.

[5]Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：Artificial Bee Colony algorithm[J].Journal of Global Optimization，2007，39（3）：459-471.

[6]暴励，曾建潮.一种双种群差分蜂群算法[J].控制理论与控制应用，2011，28（2）：266-272.

[7]汪继文，杨丹，邱剑锋，等.改进人工蜂群算法求解非线性方程组[J].安徽大学学报：自然科学版，2014，38（3）：16-23.

[8]张泰，屠思远.增强寻优能力的自适应人工蜂群算法[J].计算机应用研究：2016，33（10）.

[9]Lv Li，Han Longzhe，Fan Tanghuai，et al.Artificial bee colony algorithm with accelerating convergence[J].International Journal of Wireless and Mobile Computing，2016，10（1）：76-82.

[10]Sharma K，Gupta P C，Sharma H.Fully informed artificial bee colony algorithm[J].Journal of Experimental&Theoretical Artificial Intelligence，2016，28（1/2）：403-416.

[11]Pan Xiuqin，Lu Yong，Li Sumin，et al.An improved artificial bee colony with new search strategy[J].International Journal of Wireless and Mobile Computing，2015，9（4）：391-396.

[12]李国亮，魏振华，徐蕾.分阶段搜索的改进人工蜂群算法[J].计算机应用，2015，35（4）：1057-1061.

[13]Amira B，Amer D，Salim C.A quantum-inspired artificial bee colony algorithm for numerical optimization[C]//Proceedings of International Symposium on Programming and Systems，Algiers，2013：81-88.

[14]Zhang Song，Liu Sanyang.A novel artificial bee colony algorithm for function optimization[J].Mathematical Problems in Engineering，2015：1-10.

[15]Sharma T K，Pant M.Improved search mechanism in ABC and its application in engineering[J].Journal of Engineering Science&Technology，2015，10（1）：111-133.

[16]江铭炎，袁东风.人工蜂群算法及其应用[M].北京：科学出版社，2014：84-85.