大规模MIMO系统的改进RTS信号检测算法

王茜竹 ，李 楠

1.“新一代信息网络与终端”重庆市协同创新中心，重庆400065

2.重庆邮电大学 电子信息与网络工程研究院，重庆 400065

1 引言

随着无人机、VR智能体感设备、无人驾驶汽车等新型多样化的智能终端设备迅速普及开发，对无线数据业务需求也提出了新的挑战。面对车联网、虚拟现实、人工智能新技术的蓬勃发展，原有的无线接入网络暴露出频谱资源短缺的严重问题。为了更好地解决上述问题，大规模MIMO技术横空出世[1]。凭借着基站端配置上百根天线的优势，空间自由度大幅提升，大规模MIMO技术不仅可以提高频谱效率与信道容量，而且可以显著改善能耗效率[2]。但是大规模MIMO系统中上行链路信号检测算法复杂度随着天线数量增加呈指数增加，原有的信号检测算法无法应用在实际工程中。于是近些年业内相应提出了许多适用于大规模MIMO系统的复杂度较低的信号检测算法[3]，在这其中基于启发式思想的主动禁忌搜索（Reactive Tabu Search，RTS）算法凭借着近似于原有算法性能和复杂度较低的优势脱颖而出。由于RTS算法具备避免陷入局部极值，得到全局最优解性能，所以该算法性能优于其他基于局部近似搜索的检测算法[4]。

在Chockalingam的专著[5]中指出RTS算法性能主要取决于邻域函数定义和初始值算法的选择。初始值算法中最大似然检测（Maximum-Likelihood，ML）算法性能最优，可是因为其复杂度过高无法在工程中实现，目前通常使用的是迫零（ZF）和最小均方误差（MMSE）算法。由于天线数量上升到上百根，而ZF和MMSE算法不可避免地涉及到矩阵的求逆，所以传统基于MMSE求得初始值的RTS算法还是存在初始值计算复杂度过高的问题。基于这一问题，本文提出基于迭代算法求解初始值的改进RTS算法，并给出仿真结果和分析。

2 大规模MIMO系统模型

本文考虑的是单个小区上行链路的大规模多用户MIMO系统，在基站一侧配置M根天线，同时为天线总数为K的单天线或多天线用户服务。基于大规模MIMO系统上行链路特性，通常M≫K，发射天线个数为NK和接收天线个数为NM。假设信道模型为平坦衰落信道下的基带时域离散信号模型，则该系统复数模型为：

这里发射信号向量xc∈ℂNK，xc=[x1x2…xNK]T。接收信号向量信道增益矩阵Hc∈ℂNK×NM，假设 Hc中的所有元素服从独立同分布的复高斯分布，均值为0，方差为1。噪声向量nc∈ℂNM，假设nc中所有元素服从独立同分布的复高斯分布，均值为0，方差为 表示发射信号平均能量，γ为接收天线平均信噪比。为了便于分析，将式（1）化为实数型系统模型：

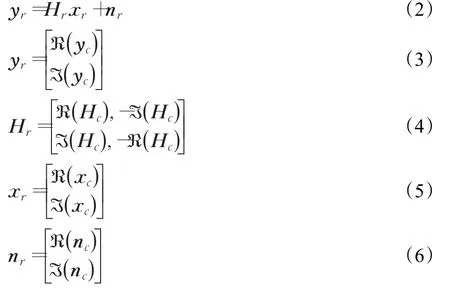
其中yr为一个2M×1维实数接收信号矩阵，xr为一个2K×1维发送信号矩阵，nr为一个2M×1维噪声信号向量，Hr为一个2M×2K维信道向量矩阵。上行链路信号检测任务就是从接收到的信号向量yr中估计出发送的信号向量xr，本文应用场景假设基站对接收端信道状态信息完全已知，也就是Hr基站接收端已知。

根据式（2）可以得到性能最优的最大似然检测（ML）算法公式为：

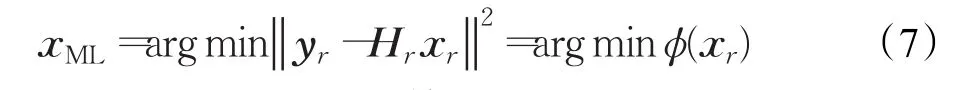
这里ML算法代价函数为：

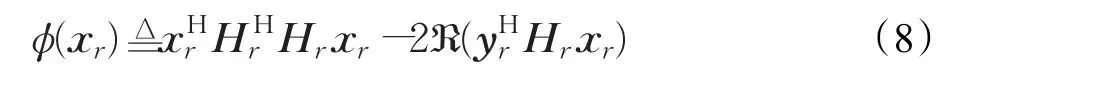
3 RTS算法

3.1 算法介绍

主动禁忌搜索算法是由Battiti和Tecchiolli将主动搜索（Reactive Search，RS）算法引入到禁忌搜索（Tabu Search）算法中得到的。RTS算法是一种基于机器学习和人工智能思想的检测算法，具备反馈机制，同时也是一种启发式算法。相比于同样基于本地邻域搜索的似然上升搜索（Likelihood Ascent Search，LAS）算法，它们共同点都是从一个初始解向量开始，接着不断尝试从当前解向量的邻域内寻找更优的解。不同点是LAS算法缺陷是容易陷入局部死循环，而RTS算法通过利用禁忌表这一反馈机制避免陷入死循环[6]。面对上百根天线数量的大规模MIMO系统，RTS算法凭借着高检测性能和复杂度低的优势成为业内研究的热点[7]。

3.2 算法实现过程

适用于大规模用于MIMO信号检测的RTS算法从初始解向量开始，这里初始解向量计算通常还是基于MIMO中传统线性信号检测算法。然后根据邻域定义的准则定义初始解向量周围的邻域，在邻域中基于上式（8）ML代价函数选出代价函数最小的最优解，即使最佳邻近向量在ML代价函数方面表现不如当前解向量，也将当前初始解向量移动到邻域向量中的最佳向量，这一举措实现了算法跳出局部最优解，得到全局最优解的效果。这样的过程经过一定数量的迭代之后，该算法被终止并得到全局最优解向量。

上述过程中解向量的邻域的定义是基于一定数量的迭代实现的，RTS算法通过标记过去几次迭代中已经移动过的解向量生成“禁忌表”（禁止再次移动到这些解向量），以确保在搜索解向量空间中避免陷入局部死循环。这些迭代的数值被定义为“禁忌周期”，其数值根据在搜索路径中观察到的解向量的重复次数动态地改变。而禁忌周期系数是为了提高算法收敛速度，提高算法性能。

4 基于RTS的改进算法

4.1 改进算法原理以及整体流程图

传统的RTS算法是从初始解向量开始的，初始解向量算法的选择很大程度决定了RTS算法的最终性能和算法实现复杂度。通过对RTS算法实现过程的分析，发现RTS算法初始解向量求解一般基于线性信号检测算法，这是因为在天线数为数十根的条件下，线性信号检测算法在复杂度方面不是很高的前提下可以获得比较优良的性能。然而当天线数量达到上百根的条件下，线性信号检测算法不可避免地进行矩阵求逆计算，信道矩阵规模大幅增加，矩阵求逆带来的算法复杂度增加问题不容小视[8]。所以本文引入基于迭代算法的信号检测算法替换传统的线性信号检测算法，应用在RTS算法中作为初始解向量求解算法。具体的基于迭代算法的改进RTS算法整体流程图如图1所示。

图1 改进的RTS流程图

4.2 线性信号检测算法求解初始解向量

初始解向量直接影响RTS算法最终的性能和复杂度，所以算法的选择至关重要。目前RTS算法初始解向量主要还是应用线性信号检测算法，比如迫零（ZF）算法[9]和最小均方误差（MMSE）算法。这里MMSE算法因为考虑到噪声因素所以性能高于ZF算法，假设发射天线数量为K，复杂度为Ο(K3)。根据文献[10]MMSE算法估计的发射信号向量x表示为：

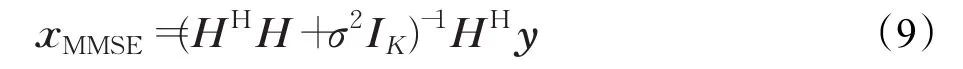
这里定义：

所以

选取MMSE作为RTS算法初始解向量算法复杂度为Ο(K3)，随着大规模MIMO系统中小区用户数量增加，应用在实际工程中还是存在复杂度过高的问题，所以考虑基于迭代算法求解初始解向量，从而避免大规模矩阵的求逆过程。

4.3 基于迭代算法求解初始解向量

在大规模MIMO系统中，随着发射和接收两端天线数量增加，天线间信道趋向正交，MMSE算法的矩阵W为对称正定性矩阵[11]。基于这一特点，考虑使用迭代算法去求MMSE算法近似发射向量x，从而降低初始值向量求解过程算法复杂度。

目前提出的迭代算法有：Neumann算法（Neumann series approximation）[12]、Richardson 算法[13]、SOR（Successive Over Relaxation）算法[14]和 GS（Gauss-Seidel）算法[15]。这些算法通过应用在大规模MIMO系统下RTS算法仿真得出，随着迭代次数增加Neumann算法复杂度过高，Richardson算法性能居中，而SOR和GS算法可以得到近似于MMSE的初始解向量结果。虽然SOR算法收敛速度最快，但是相比GS算法复杂度高，所以本文选择GS迭代算法作为RTS算法初始解向量求解算法。并在GS算法基础上提出块分星座图的BC-GS（Block-Constellations GS）优化算法，从而进一步降低算法复杂度。

GS算法应用在求解N维线性方程：

其中A是N×N维Hermitian正定矩阵，x是N×1解向量，b是N×1向量。不同于传统方法直接计算A-1b得到x，GS方法可以通过迭代方法求解方程Ax=b，降低复杂度。当小区基站天线数为M，小区用户天线总数为K，MMSE转换矩阵W是2K×2K维Hermitian正定矩阵，公式（13）和公式（14）也是一样类型，综上所述，可以分解W为：

这里D代表矩阵W的对角元素组成的矩阵，L代表矩阵W的严格下三角元素组成的矩阵，U代表矩阵W的严格上三角元素组成的矩阵。根据GS算法公式（14）可以得到：

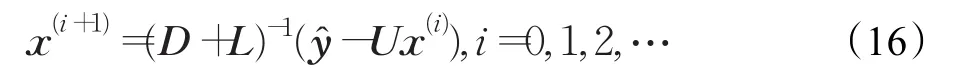
通常当i=0，作为GS迭代算法的初始解向量x(0)=为2K×1的零向量矩阵[16]。提出基于块分星座图的思想重新定义初始值，从而进一步提高GS迭代算法性能，并且BC-GS算法可以更好地应用在高阶调制中。

首先定义xi和为发射向量x和接收向量 y的第i个元素，而表示矩阵W的第i行和第 j列元素。

根据文献[17]得到，大规模MIMO随着天线增多，出现信道硬化的趋势，即矩阵W为对角元素占优矩阵（对角元素相对于非对角元素数值大很多），当然W-1也是对角占优矩阵。又因为W是对称正定矩阵，对角元素都是正数。得出：

根据上式可以判断接收向量的正负，从而判断发射向量xi的正负，基于这一点再将映射的星座图划分为A块，然后界定每块区域的边界值，通过算法确定xi属于哪个小区域，然后选取该区域的中心点最为初始解向量。基于块分星座图定义初始值实现过程如下：

（1）确定块分星座图区域个数A，根据调制确定映射星座图Q值和

（2）定义块分小区域边界值为：

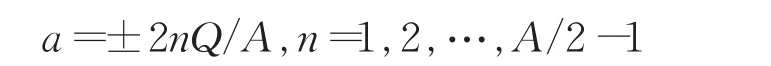
（3）根据进行判定所在区域：大于0，并选取该区域的中心点作为；如果当小于0，xi⊂选取该区域的中心点作为

（4）结束。

下面通过具体实例对上述过程说明基于块分星座图思想定义初始值过程。假设应用64QAM调制方式，所以xi可能是{ }-7,-5,-3,-1,+1,+3,+5,+7 ，即Q=8。定义A=4，也就是块分为4个小区域，所以根据步骤（2）得到区域边界值a=4,4。然后根据的值确定所在区域，比如假设，并且范围就在[0，4]之间，选取=2；如果-Wa<0，范围就在[4，8]之间，选取=6；当<0则反之。通过图2可以清楚地发现通过对GS算法引入块分星座图思想，初始值向量到发射向量距离d1明显比零向量到发射向量距离d2小，从而提高精确度，减少迭代次数，提高算法性能。

图2 BC-GS算法与传统GS算法初始解对比

所以根据公式（15）、（16），可以得到基于块分星座图思想定义的BC-GS算法流程如下：

（1）W矩阵分解为W=D+L+U；

（2）基于块分星座图思想求解GS算法初始解向量：

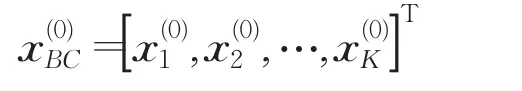
（3）计算（i表示迭代次数）：

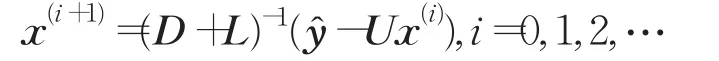
（4）i=i+1；

（5）重复进行步骤（1）～（4），得到向量序列 x(i)；

（6）结束。

5 改进的RTS算法复杂度分析

由于本文的改进RTS算法主要是对初始解向量算法进行优化，即提出BC-GS算法来替换MMSE算法作为初始解向量算法，从而减低RTS算法整体复杂度，提高算法性能。于是改进的RTS算法和传统的RTS复杂度的对比其实也就是BC-GS和MMSE算法复杂度的对比。

BC-GS算法复杂度主要分为两部分：（1）GS迭代算法本身的复杂度；（2）基于块分星座图思想改进的初始解向量算法带来的复杂度。

首先计算GS算法本身的复杂度。根据公式（16），可以将迭代方程变化为：

上式中左式2K×2K维矩阵(D +L)和2K维矩阵x(i+1)相乘次数为2K2+K，等式右边2K×2K维矩阵U和2K×1维矩阵x(i)相乘次数为2K2-K。所以进行一次GS算法需要4K2次相乘。

其次分析基于BC思想初始值求解复杂度。这部分算法复杂度主要集中在这一步骤。W为一个2K×2K维矩阵，而a为一个2K×1维只有第i个元素为常数，其他元素为0的矩阵。所以相乘次数为2K。

综上所述进行一次BC-GS算法所需4K2+2K次计算。而MMSE算法复杂度为K3。具体两种算法对比如表1所示。

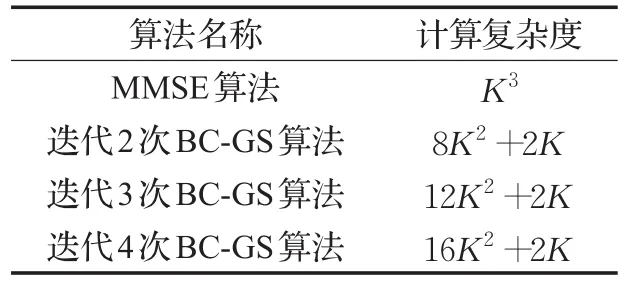
表1 计算复杂度对比

引入块分星座图思想求解初始值的BC-GS算法不仅使GS算法更适用于64QAM高阶调制方式，而且使复杂度相比传统GS算法也有所降低。例如图3中，经过两次迭代GS算法复杂度为18K2+4K，而BC-GS算法复杂度为8K2+2K。从图3中，可以发现随着迭代次数增加，GS和BC-GS算法复杂度都有所增加，而在三种算法中MMSE算法的复杂度是最高的，GS算法复杂度居中，而改进的BC-GS算法复杂度最低。例如在小区用户数为35（这里默认小区用户都为单天线用户，小区用户数等同于小区用户天线数）的条件下，MMSE复杂度为4.25×104，而迭代次数为4的GS和BC-GS算法复杂度为2.5×104和1.4×104。具体MMSE、GS、BC-GS三种算法复杂度对比如图3所示。

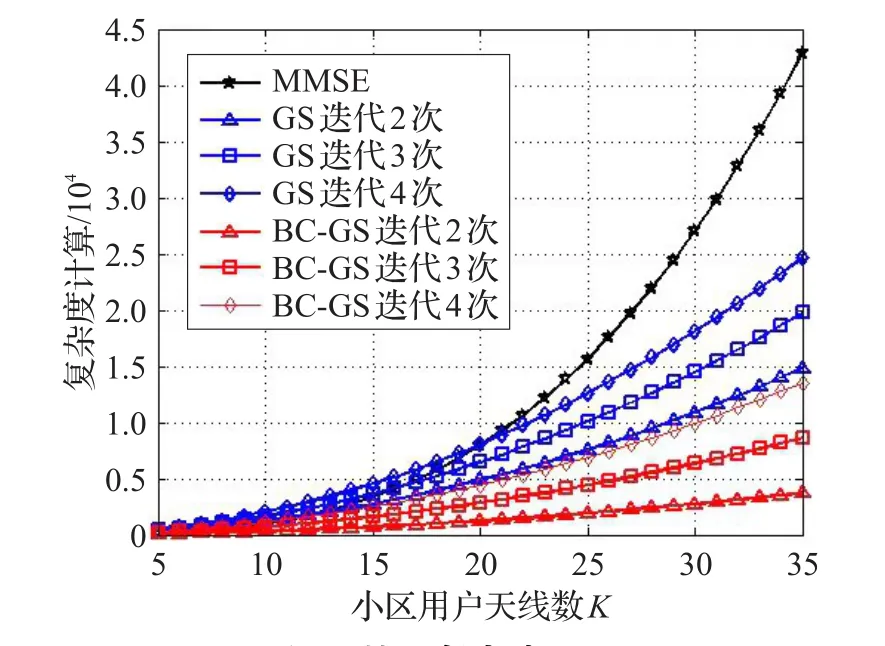
图3 算法复杂度对比

6 仿真结果分析

通过仿真，从误码率性能方面进行算法对比，从而验证改进的RTS算法在复杂度有所降低的前提下，性能在迭代次数一定的条件下几乎没有受到损失。

首先根据大规模MIMO系统配置初始仿真参数，具体参数配置如表2。

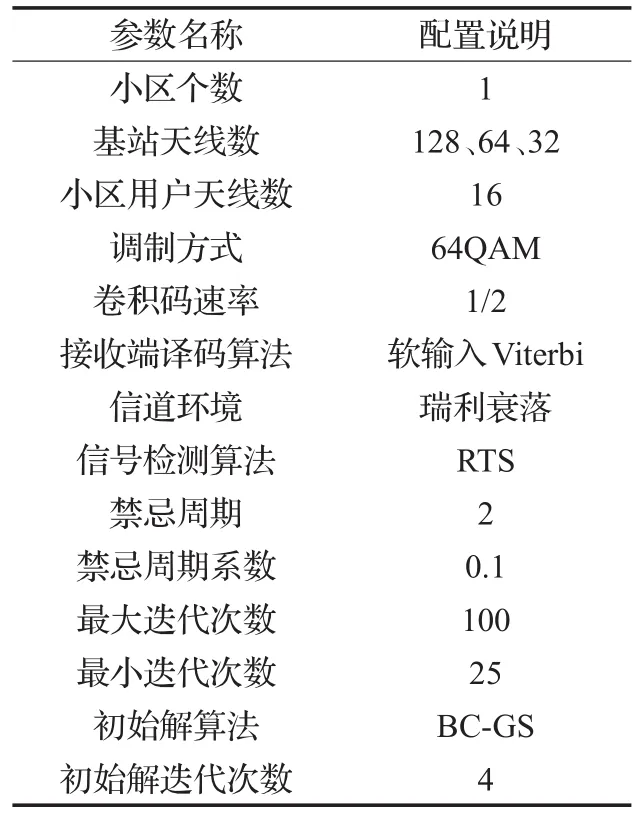
表2 初始仿真参数配置

这里针对表2小区用户天线数加以说明，根据大规模MIMO系统在基站端布置大规模天线阵列特性，带来的系统性能提升也主要来自于基站端，所以本文为了便于分析改进算法性能将初始仿真参数小区用户天线数固定为16根。

然后根据表2的相应参数，分别对MMSE、GS和BC-GS三种初始解向量算法进行BER对比。在图4中可以看出MMSE的BER性能最好，随着迭代次数增加，GS和BC-GS算法的BER性能逐渐提高。而凭借着块分星座图思想求解初始值的BC-GS算法在同样迭代次数条件下，BER性能明显好于GS算法。在迭代次数为4时，BC-GS算法的BER性能已经十分接近MMSE算法。例如当SNR为12 dB时，迭代4次的BC-GS算法的BER仅比MMSE算法高2×10－6，但是算法复杂度确实明显降低很多。

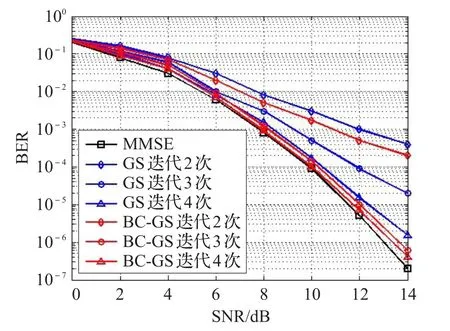
图4 三种初始值算法BER对比

其次根据表2配置小区用户天线总数为16，基站天线数目分别为32、64、128，禁忌周期为2，禁忌周期系数为0.1，设定最大迭代次数为100，最小迭代次数为25的系统参数下对改进的RTS算法（基于BC-GS作为初始解向量）和原来的RTS算法（基于MMSE最为初始解向量）进行BER对比。这里BC-GS初始解向量算法迭代次数为4，因为从图4发现迭代次数为4时，BER性能最接近MMSE算法。从图5中，可以看出随着基站天线数量的增加，BER性能得到改善，比如在SNR为40 dB时，64×16的RTS算法BER比32×16降低1.9×10－4，128×16的BER比64×16降低8×10－5。而且可以看出虽然改进的RTS算法复杂度降低很多，可是BER性能却没有受到很大影响，不论基站天线数的改变，始终BER性能都是很接近原来的RTS算法。例如在SNR为40 dB时32×16的改进RTS的BER只比原来的RTS算法高2×10－5，64×16的改进RTS的BER比原来的RTS算法高3×10－5，而天线数128×16的改进RTS算法的BER只比原来的RTS算法高7×10－5。

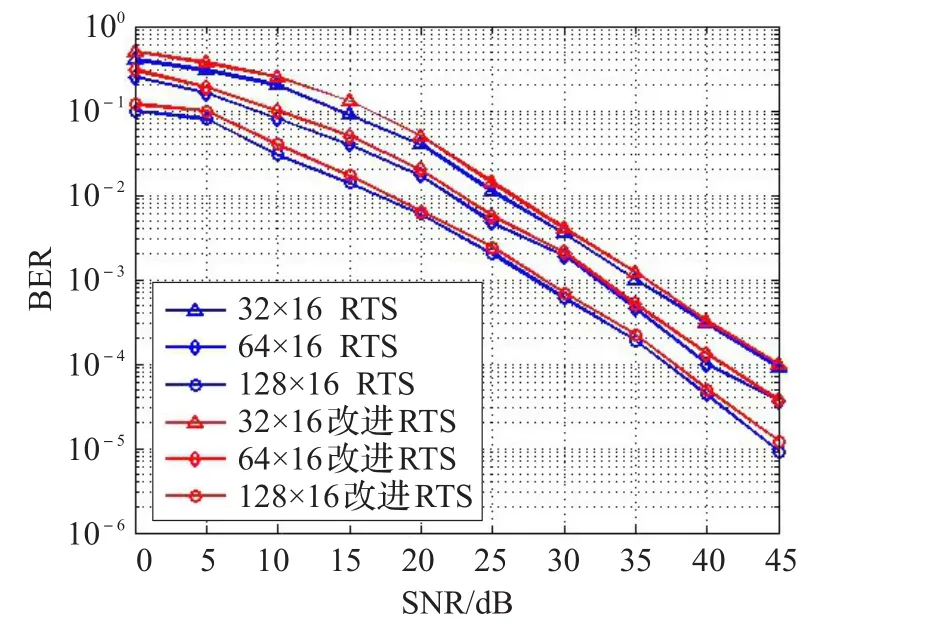
图5 改进RTS和原来RTS算法BER对比

接着分析改进算法的收敛性，通过不同迭代次数下算法性能的变化来验证这一性质。在表2配置的基础上，又增加信噪比为30 dB这一限定条件和小区用户天线数为32这一情况。从图6中，可以看出随着迭代次数的增加，不论天线数为32×16、64×16还是128×16性能都呈现出收敛性，特别是迭代次数超过70以后，这一趋势更加明显。例如，当天线数为128×16，迭代次数为70时，改进算法BER为1.1×10－4，迭代次数增加到100时，BER为0.7×10－4，只比迭代70时低4×10－5。所以随着迭代次数的递增，改进算法性能表现出稳定和优良的趋势。这里选取单输入单输出系统的高斯白噪声信道性能作为参考标准。

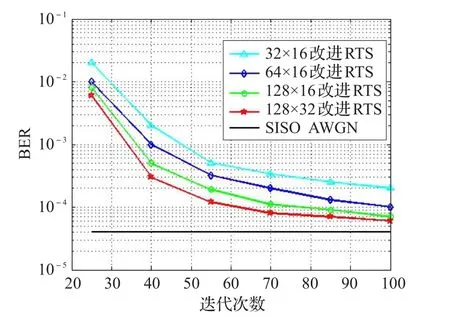
图6 不同迭代次数下改进算法BER对比

最后针对小区用户天线数对算法性能的影响做简单描述。从图6中，通过对比天线数128×16和128×32的BER，可以看出随着小区用户天线数从16增加到32性能有所提升。例如在迭代次数为70时，128×32的BER比128×16低3×10－5。所以小区用户天线数量的增加也可带来性能的改善，不过牺牲的是复杂度的相应提升。

7 结束语

本文首先对GS迭代算法进行改进，提出块分星座图思想求解初始值替换原有初始零向量的BC-GS算法，从而算法复杂度进一步降低，并且也更适用于高阶调制方式下。然后基于BC-GS迭代求解算法替代原来的MMSE算法，作为RTS算法的初始解向量算法，从而在迭代次数一定的条件下，降低算法的复杂度，而改进的RTS算法的性能也没有受到很大损失，更加利于工程实现。

[1]Marzetta T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications，2010，9（11）：3590-3600.

[2]Ngo H，Larsson E，Marzetta T.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications，2012，61（4）：1436-1449.

[3]Wu M，Yin B，Wang G，et al.Large-scale MIMO detection for 3GPP LTE：Algorithms and FPGA implementations[J].IEEE Journal of Selected Topics in Signal Processing，2014，8（5）：916-929.

[4]Datta T，Srinidhi N，Chockalingam A，et al.Random restart reactive tabu search algorithm for detection in large-MIMO systems[J].IEEE Communications Letters，2010，14（12）：1107-1109.

[5]Chockalingam A，Rajan B S.Large MIMO systems[M].[S.l.]：Cambridge University Press，2014.

[6]张中山，王兴.大规模MIMO关键技术研究及应用[J].中国科学：信息科学，2015，45（9）：1095-1110.

[7]Yang Shaoshi，Hanzo L.Fifty years of MIMO detection：The road to large-scale MIMOs[J].IEEE Communications Surverys&Tutorals，2015，17（4）：1941-1988.

[8]Rusek F，Persson D，Lau B K，et al.Scaling up MIMO：Opportunities and challenges with very large arrays[J].Signal Processing Magazine IEEE，2013，30（1）：40-60.

[9]Gao X，Dai L，Ma Y，et al.Low-complexity near-optimal signal detection for uplink large-scale MIMO systems[J].Electronics Letters，2014，50（18）：1326-1328.

[10]Yin B，Wu M，Studer C，et al.Implementation trade-offs for linear detection in large-scale MIMO systems[C]//IEEE International Conference on Acoustics，Speech and Signal Processing（ICASSP’13），2013：2679-2683.

[11]Larsson E，Edfors O.Massive MIMO for next generation wireless systems[J].IEEE Communications Magazine，2013，52（2）：186-195.

[12]Wu M，Yin B，Vosoughi A，et al.Approximate matrix inversion for high-throughput data detection in the largescale MIMO uplink[C]//IEEE International Symposium on Circuits and Systems，2013：2155-2158.

[13]Gao X，Dai L，Yuen C.Low-complexity MMSE signal detection based on Richardson method for large scale MIMO Systems[C]//Vehicular Technology Conference（VTC Fall），2014：1-5.

[14]秦闯，郑紫微，娄达平.基于近似信息传递算法的大规模MIMO信号检测[J].电信科学，2016，32（9）：16-20.

[15]Qian M，Wang Y，Zhou Y.A super base station based centralized network architecture for 5G mobile communication systems[J].DigitalCommunicationsand Networks，2015，54（2）：152-159.

[16]Bjork A.Numerical methods in matrix computations[M]//Texts in Applied Mathematics.[S.l.]：Springer International Publishing，2015.

[17]Tulino A，Verdu S.Random matrix theory and wireless communications[J].Foundations and Trends in Communications and Information Theory，2004，1（1）：1-182.