综合TOPSIS法和RSR法对医院运行管理的评价

郭文燕, 梅文华, 方国伦, 刘军卫, 江鸿, 叶仲书, 郭伟文

医院运行质量管理工作是一个多因素多指标的复杂系统,单用某个指标对其进行评价已经不适用,必须用多指标综合评价的方法,才能较为全面、客观地反映出医院运行管理的状况。秩和比(rank sum ratio,RSR)法是非参数的统计方法,其综合了多项评价指标的信息,表明多个指标的综合水平,被广泛运用于综合评价和分组中[1-2]。TOPSIS(technique for order preference by similarity to ideal solution)法是系统工程中有限方案多目标决策分析中的一种决策方法,其运用灵活、结果量化、客观合理,在医院综合服务质量评价、卫生决策、卫生事业管理等多个领域中广泛运用[3]。本文运用RSR法、TOPSIS法、TOPSIS和RSR相结合的方法,分别对2016年某市7家公立医院的运行管理情况进行综合评价和分析,找出各医院间的不足和差距,为卫生行政和医院管理部门制定决策提供科学依据,从而全面提高医院管理水平与竞争力。

1　资料和方法

1.1　资料来源

本研究涉及的7家公立医院,除医院G外,均为三级医院。研究数据来源于2016年《广东省卫生计生统计信息网络直报系统》,其中满意度指标由暨南大学基础医学院流行病与卫生统计教研室现场调查收集,医院医疗纠纷统计数据由市医疗纠纷人民调解委员会提供。本研究参考《公立医院绩效评价指标体系(试行)》,查阅相关文献资料[4-6],遵循有意义、能明显区分优差等级、与医改同步、代表性强、指标相关性不强的原则,选取医疗服务效率、管理水平、医疗费用、医疗服务质量、满意度5个方面17项指标进行综合评价和分析。医疗服务效率指标包括X1(医师人均每日担负诊疗人次)、X2(医师人均每日担负住院床日)、X3(病床周转次数)、X4(病床使用率)、X5(出院者平均住院日);管理水平指标包括X6(管理费支出占业务收入比例)、X7(药品收入占业务收入比例)、X8(药品收入占业务收入比例同比下降率)、X9(卫生材料收入占业务收入比例)、X10(每医生业务收入)、X11(百元医疗收入成本)、X12(人员支出占业务支出比例);医疗费用指标包括X13(次均门诊费用)、X14(次均住院费用);医疗服务质量指标包括X15(每百床医疗纠纷案件数);满意度指标包括X16(患者满意度)、X17(职工满意度)。

1.2　研究方法

1.2.1RSR法 ①编秩、计算RSR值、排序。拟纳入的17项指标中有8项低优指标,包括X5、X6、X7、X9、X11、X13、X14、X15,其余均为高优指标。高优指标由小到大进行编秩,低优指标由大到小进行编秩。运用计算各医院运行管理情况的秩和比,并按其大小进行排序。其中,m为指标数;n为医院数[7]。②确定RSR的分布,计算回归方程、分档。以RSR值由小到大排序,列出不同组段的频数(ƒ),累计频数(∑ƒ),秩次(R),平均秩次(),向下累计频率[(/n)×100%],并将百分率p换算成概率单位Probit[8],再建立Probit与Ci的回归方程、分档[7]。

1.2.2TOSIS法 ①同趋势化处理。建立数据矩阵,将指标同趋势化,通常将低优指标转化成高优指标[9]。绝对数指标用倒数法(100/Xi)进行转换,包括X5、X11、X13、X14、X15;相对数 指 标 用 差 值法(100-Xi)进行转换,包括X6、X7、X9。②归一化处理。对同趋势化后的数据矩阵进行归一化处理,建立归一化矩阵…,7;j=1,2,…,17,采用Excel函数计算。③确定最优向量Z+和最劣向量Z-。其中,=max=min{Zij},i=1,2,…,7。④根据Zj+和确定最优值的距离Di+、最劣值的值的距离以及Ci值,并进行排序[11]:

1.2.3TOPSIS和RSR相结合的方法 TOPSIS法方法简便、运用灵活,可充分利用原始数据信息,数据损失较少,但不能进行分档。在TOPSIS法的基础上,结合RSR法对Ci值进一步分析,对评价对象可以排序的同时也可以分档,不仅可弥补TOPSIS法的不足,又能改善RSR法直接取秩次进行分析评价时损失部分信息的弊端,做到了优势互补[12]。

2　结果

2.1　RSR法的应用

2.1.1用RSR法对原始数据进行处理 根据指标的性质编秩,计算RSR值并排序,确定RSR的分布。见表1及表2。

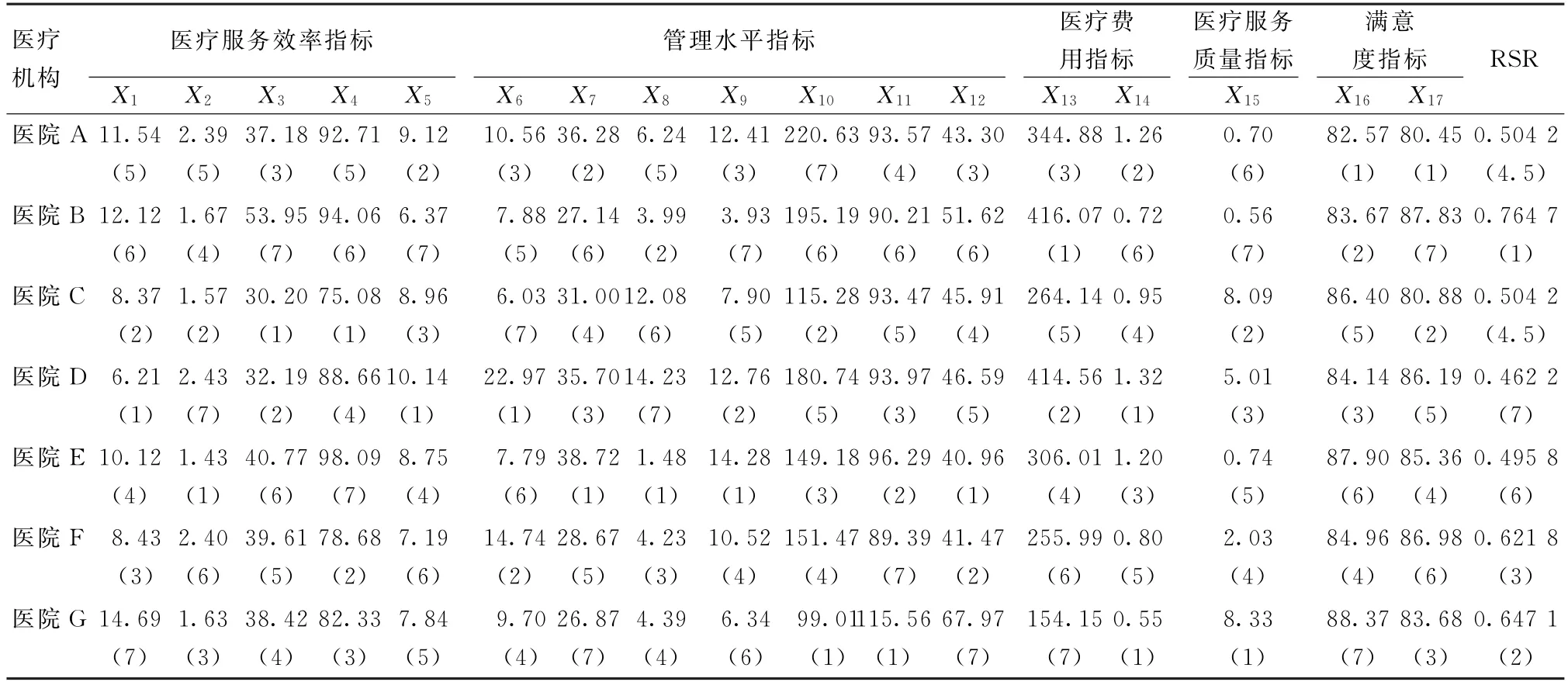
表1　2016年某市7家公立医院17项指标的秩次和RSR值

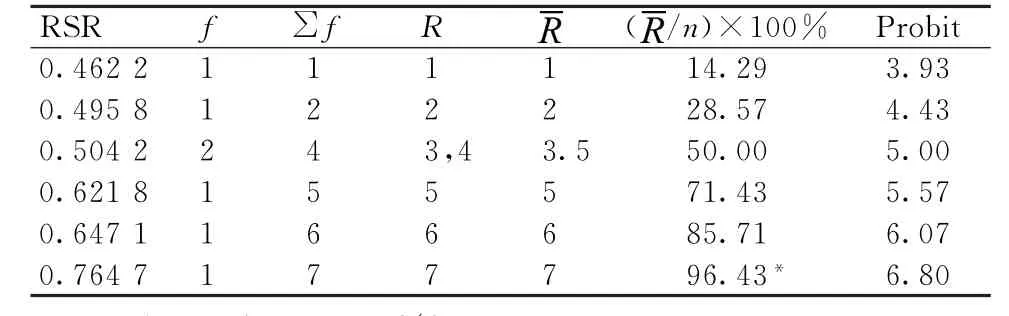
表2　RSR值的频数分布及概率单位

2.1.2计算回归方程与分档 对RSR值进行正态分布检验,符合正态分布;经相关性分析,Probit与RSR相关系数r=0.972,具有统计学意义(P=0.001),说明Probit与RSR呈正相关关系。以累计频率所对应的概率单位值Probit为自变量,以RSR值为因变量,建立回归方程,RSR=0.021+0.106 Probit,回归方程具有统计学意义(P=0.001),且R2=0.944,提示模型拟合优度好。结合最佳分档原则和合理分档数表,先拟将7家公立医院的运行管理情况分为3档。见表3。

由表3可知,该市7家公立医院的运行管理状况分为上、中、下3档。方差齐性检验显示,各档方差一致(P=0.810);但方差分析结果表明,各档间差异无统计学意义(P=0.126)。

表3　2016年某市7家医院运行管理情况基于RSR值的分档

由于各档间差异无统计学意义,再拟将7家公立医院的运行管理情况分为4档。无任何一家医院归为差档,故7家公立医院的运行管理情况实际分为优、良、中3档,其中优档为医院B,良档为医院F、G,中档为医院A、C、D、E。方差齐性检验显示,各档方差一致(P=0.555);方差分析结果显示,各档间差异具有统计学意义(P=0.003)。见表4。

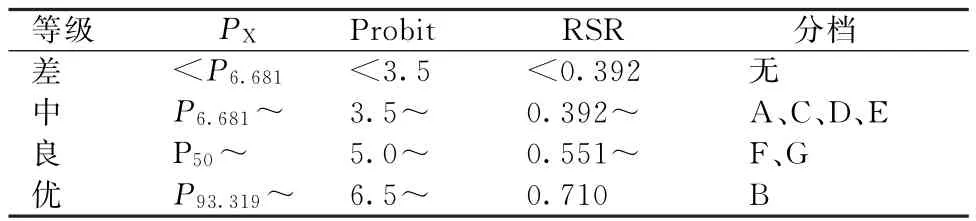
表4　2016年某市7家医院运行管理情况基于RSR值分成4档的分档

2.2　用TOPSIS法对原始数据进行处理

将表1中的原始数据进行同趋势化和归一化处理,得到矩阵Z,其最优向量和最劣向量分别为:

Z+=(0.526 7,0.464 8,0.515 6,0.424 3,0.478 8,0.400 1,0.405 9,0.676 4,0.402 0,0.509 2,0.402 6,0.523 9,0.641 3,0.580 7,0.657 9,0.390 9,0.392 7)

Z-=(0.222 6,0.273 5,0.288 6,0.324 8,0.300 7,0.327 9,0.340 2,0.070 3,0.358 7,0.228 5,0.312 7,0.315 7,0.236 8,0.242 0,0.045 5,0.365 2,0.359 7)

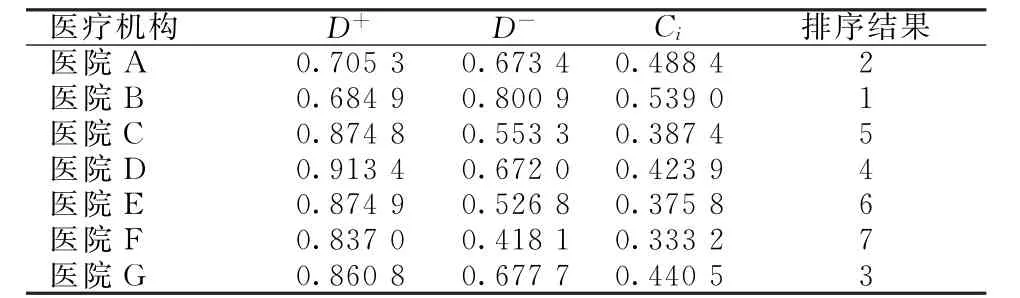
表5　2016年某市7家医院运行管理情况TOPSIS综合评价结果及排序

2.3　结合RSR法对Ci值作进一步处理

以Ci值由小到大排序,列出不同组段的频数(ƒ),累计频数(∑ƒ),秩次(R),平均秩次(),向下累计频率(/n×100%),并将百分率p换算成概率单位Probit[8]。见表6。

表6　Ci值的频数分布及概率单位

计算回归方程与分档。对RSR值进行正态分布检验,符合正态分布;经相关性分析,Probit与Ci相关系数r=0.996,具有统计学意义(P＜0.000 1),说明Probit与Ci呈正相关关系。以累计频率所对应的概率单位值Probit为自变量,以Ci值为因变量,建立回归方程,Ci=0.053+0.071 Probit,回归方程具有统计学意义(P＜0.000 1)。且R2=0.992,提示模型拟合优度较好。分析显示,该市7家公立医院的运行管理状况分为上、中、下3档,其中上档为医院A、B,中档为医院C、D、E、G,下档为医院F。方差齐性检验显示,各档方差一致(P=1.000);方差分析结果表明,各档间差异具有统计学意义(P=0.019)。见表7。

表7　2016年某市7家医院运行管理情况综合TOPSIS法和RSR法的分档排序

3　讨论

3.1　评价方法分析

采用横向比较法对各医院的指标进行比较,可以在一定程度上反映各医院运行管理情况,发现自身不足与差距,并发挥自身优势,改善不足,有利于医院的发展[13]。RSR法综合能力较强,综合了多项指标的信息,且对离群值不敏感,但直接取秩次信息进行评价会导致损失部分信息[14]。RSR法得到的回归方程的R2为0.944,分别对分成3档与4档的结果进行方差齐性检验与方差分析,均具有方差一致性。若分成3档,各档之间差异无统计学意义;若分成4档,各档之间差异具有统计学意义。TOPSIS法方法简单、运用灵活,充分利用原始数据的信息,对原始数据进行同趋势化、归一化处理后,消除了量纲的影响,能定量评价不同指标的优劣程度,但易受异常值影响。TOPSIS和RSR联合法得到的回归方程的R2为0.992,大于仅用RSR法求得的R2值,提示模型拟合优度更好,且各档间差异均具有统计学意义。通过两者联合的方法,对TOPSIS法的排序结果作RSR分档分析,充分利用了原始数据信息,克服了TOPSIS法不能分档评价,RSR法直接取秩次评价而损失部分信息的局限性,起到优势互补的作用,更加科学、全面、客观地反映出各医院的实际运行管理情况,与医院的实际相符,因此宜推广应用。

3.2　评价结果分析

医院B是一所专科医院,与综合医院比较具有一定的优势,如每位医生工作量饱和,病床周转率和使用率高,次均出院费用、药费占比和运行管理费用低,但其门诊、住院费用较高,运行管理费用较大。医院B应加强医院内部的建设,降低运行管理费用占比,在诊治病人的同时,减轻患者的经济负担,争取让每一位患者享受到质高价廉的医院服务。医院C的病床周转次数、病床使用率处于7家医院中的最低水平,且每百床医疗纠纷案件数较高。医院C应提高医院诊疗水平,提高收治病人质量,在诊治常见病、多发病的基础上,发展重点专科和特色专科,吸引更多的患者,提高床周转次数和病床使用率。医院D的医师人均每日负担诊疗人次少,出院者平均住院日高。可能因为其是该市规模最大的综合医院,也是卫生技术人员、床位数最多的医院。医院D应规范诊疗流程,提高住院各环节的效率,减少相对低效的诊疗服务时间,缩短平均住院日[16-17]。医院E的医师人均每日负担住院床日少,药品收入、卫生材料收入占业务收入的比例高,可能与该院是中医院有关。虽然珠海市已于2015年3月29日实施药品和医用耗材零差率政策,但该政策不包括中药饮片,未对该院的药费占比起到显著作用。医院E的人员支出占比在7家医院中比较差,提示应提高医务人员的福利待遇。医院G是7家医院中唯一的二级医院,每百床医疗纠纷案件数明显高于其他医院,医生业务收入低,百元医疗收入成本较高,提示应加大对医疗成本的控制,减少浪费;医护人员提高医疗技术水平的同时也要学习医患之间沟通的技巧,耐心对待患者及家属。医院F处于最下档,提示需要进行全面监管与改进管理,特别是在病床使用率、管理费支出占业务支出的比例、人员支出占业务支出的比例等方面。

综上所述,运用TOPSIS和RSR相结合的综合评价法能客观综合反映医院的运行管理情况,克服以往单一评价方法的局限性,且与医院实际情况一致,适宜在医院运行管理评价中推广运用。

参考文献