基于正交试验的空间绳网展开参数灵敏度分析*

刘海涛 杨乐平 张青斌 宋旭民

(1.航天工程大学,北京 101416) (2.国防科技大学空天科学学院,长沙 410073)

引言

近年来,空间绳网捕获在非合作目标捕获、远距离捕获等方面展现了极大的应用潜力,受到了航天领域日益广泛的关注[1-3].如图1所示,轨道拖船机动接近目标后,利用发射机构为连接于绳网顶点的质量块提供初始动量,质量块牵引绳网展开并向前飞行,绳网与目标接触碰撞后包裹目标,此时通过收口机构(内置于质量块)将网口收拢并锁死,从而形成拖船与目标的可靠连接[3].

图1 空间绳网捕获示意图Fig.1 Sketch map of space net capture

空间绳网的展开效果是空间绳网捕获任务成功的关键所在,因此需要考察影响空间绳网展开效果的多个设计参数,对其进行灵敏度分析,即分析空间绳网展开的性能指标对各设计参数的敏感程度.目前已有学者利用空间绳网展开仿真试验,对影响空间绳网展开效果的设计参数进行研究.陈钦等[4]讨论了发射角度和绳索阻尼对展开面积的影响,并给出了这两个参数在一定的系统配置下的最优值.李京阳等[5]提出了飞网展开效果衡量标准,分析了质量块质量、抛射速度、抛射角度以及绳索阻尼等抛射参数对多个性能指标的影响规律.然而在这些研究中,都只对设计参数逐个进行了分析,没有体现多个设计参数之间的交互作用.

影响空间绳网展开效果的设计参数数量较多,为了全面分析不同设计参数的交互作用,需要进行大量的仿真试验.考虑到空间绳网的仿真模型较为复杂,单次空间绳网展开的程序运算时间较长,为了节省仿真试验的时间,需要采用合适的试验设计方法以减小试验次数.正交试验设计是依据正交表,从所有因素的所有水平可能的组合中挑选部分有代表性的组合进行试验的一种试验设计方法[6-8],该方法可在大幅度精简试验次数的同时,不失试验的代表性.正交试验的结果具有正交性、典型性以及综合可比性等优点,可以应用极差分析、方差分析等方法对试验结果进行灵敏度分析,得出很多有价值的结论[6].近年来,正交试验设计方法已在系统参数分析方面得到了广泛的应用[9-11].

本文针对影响空间绳网展开效果的设计参数开展灵敏度分析.首先定义空间绳网展开效果的性能指标和设计参数；然后基于正交试验设计安排仿真试验,获得各设计参数不同水平值条件下对应的各性能指标值,也就是正交试验结果；然后介绍针对正交试验结果进行分析处理的极差法和方差法；最后综合运用极差法和方差法,对正交试验结果的各项性能指标依次进行参数灵敏度分析,此外还对各指标的相关性进行分析.

1 性能指标与设计参数

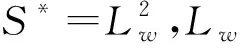
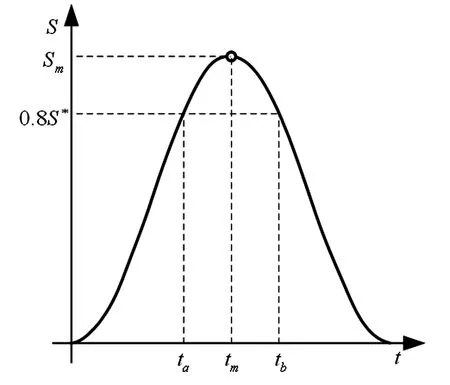
图2 基于展开面积的性能指标Fig.2 Performance index based on the deployment area

这些性能指标中,最大展开面积Sm表征了空间绳网所能展开的最大程度,决定了所能捕获目标的极限尺寸；最大展开时间tm表征了空间绳网展开过程的快速程度；最大展开距离dm和有效作用距离de分别表征了空间绳网的最佳捕获距离以及作用范围的大小.

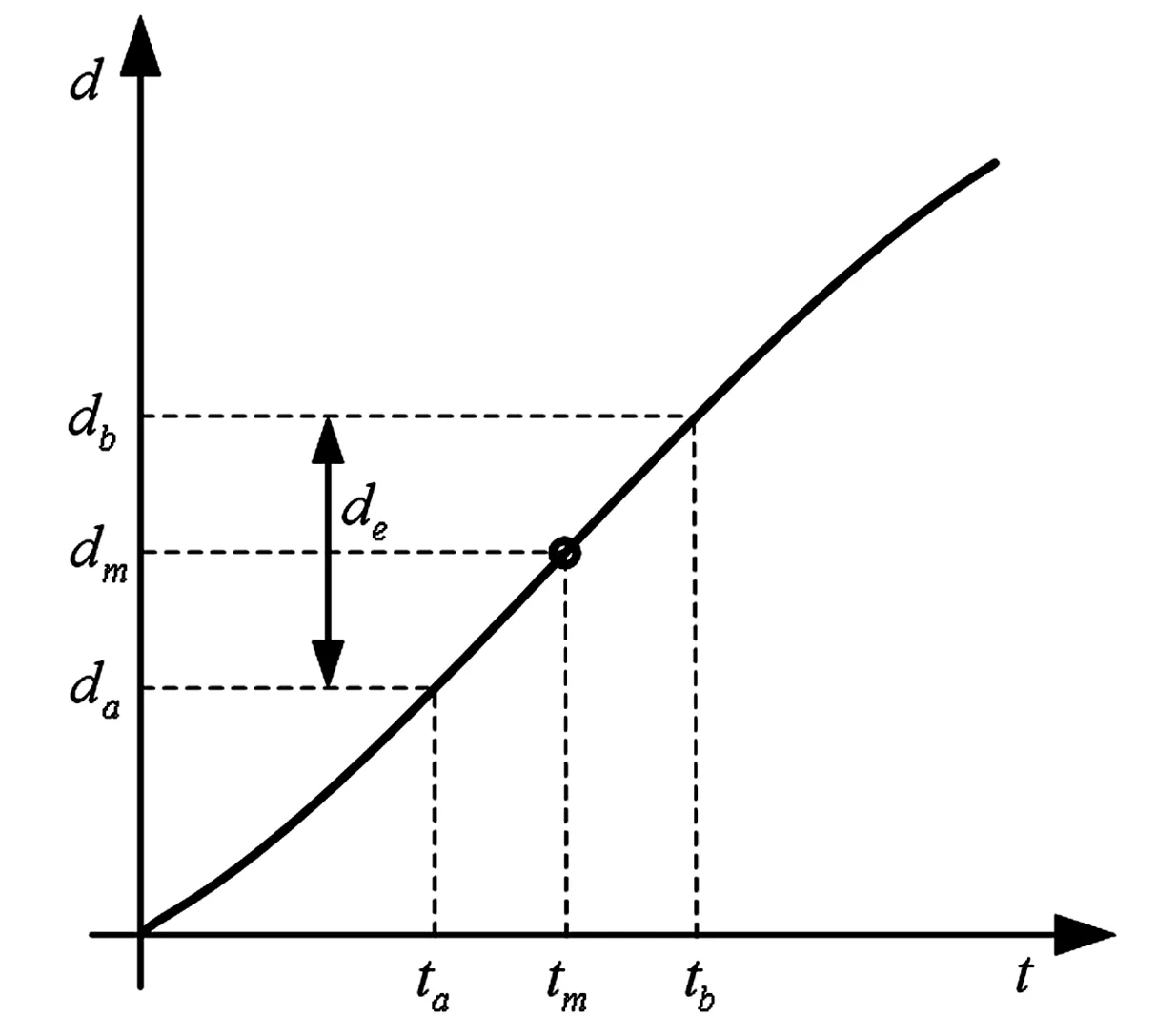
图3 基于飞行距离的性能指标Fig.3 Performance index based on the flight distance

结合相关文献并通过初步仿真分析,影响空间绳网展开效果的设计参数有绳网边长Lw、绳网质量mw、质量块质量ms、发射速率υ、发射张角α及绳索阻尼比ζ等.考虑到工程中绳网边长Lw主要是根据待捕获目标的尺寸而选取相应的大小,因此Lw不作为待优化参数,而是在下面的分析中将其设为常量,重点考察其它五个设计参数.

2 基于正交试验的仿真试验

一次空间绳网展开仿真试验即为运行一次空间绳网展开程序,仿真中,目标位于GEO轨道,拖船位于目标V-bar方向,绳网材料为Zylon®纤维,绳网边长固定为Lw=40m.由于空间绳网的仿真模型较为复杂,单次空间绳网展开的程序运算时间往往耗时数个小时,因此对所有仿真参数进行全析因试验的时间消耗难以承受.为了减少仿真试验次数,同时不失试验的代表性,下面通过正交试验设计方法来安排仿真试验.

在正交试验设计中,试验因素为上述五个设计参数,各因素划分为表1所示的五个水平.

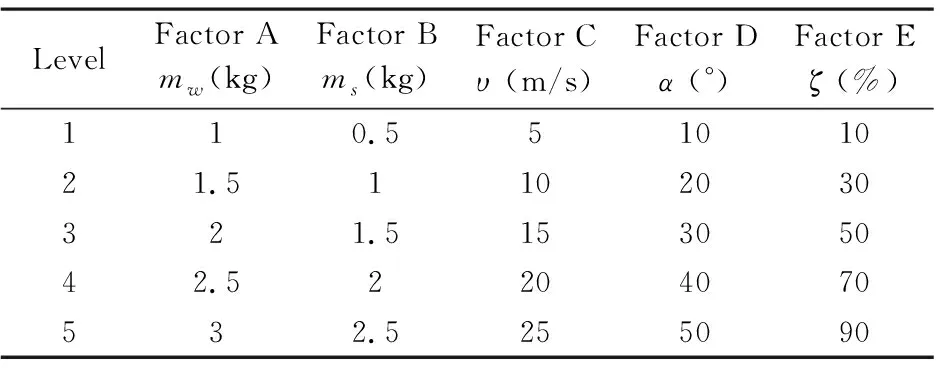
表1 正交试验设计的因素与水平Table 1 Factor and level of the orthogonal test design

如表2所示,根据正交表L25(56)的前五列安排仿真试验,最后一列作为空列模拟误差项.从表2可以看出,正交表具有如下性质:任一列中各水平都出现,且出现次数相等；任两列间各种不同水平的所有可能组合都出现,且出现次数相等.因此根据正交表安排的试验,具有“均匀分散、齐整可比”的特点.从表2还可看出,本文正交试验的总试验次数为25次,远远低于相同因素和水平的全析因试验的55=3125次,体现了正交试验设计能大大减少试验次数的优势.

仿真试验中,绳网质量mw、质量块质量ms、发射速率υ、发射张角α及绳索阻尼比ζ根据表2进行取值,仿真得到的各项性能指标的数值如表2中右侧四列所示.

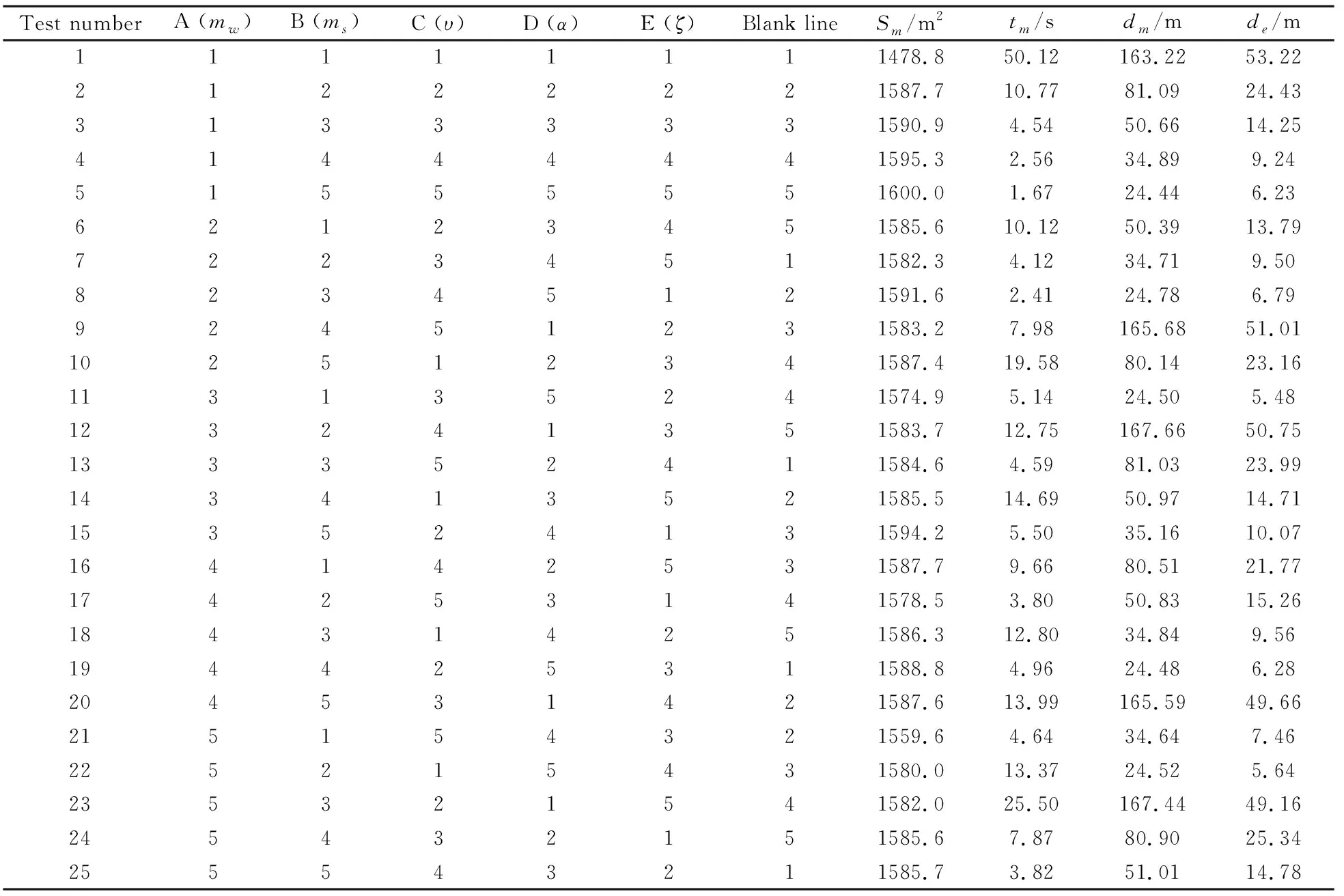
表2 正交试验及其结果Table 2 Orthogonal test and its results

3 正交试验结果的分析方法

针对正交试验结果的灵敏度分析方法主要包括极差法和方差法[7,8].

3.1 极差法

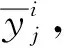
(1)

式中,pj为第j因素所划分水平的数目.Rj越大说明该因素对该指标的影响越大,该因素越重要,据此可将各因素按重要性进行排序.极差法的优点在于简单直观,计算量少,但是它无法估计试验误差的大小,也无法提出一个标准来判断因素的作用是否显著.

3.2 方差法

方差法的基本思想是将指标值的总离差分解成因素的水平变化引起的离差和误差引起的离差两部分,然后构造F统计量,作F检验,从而判断因素的显著程度.设因素j的水平变化引起某指标值的离差为:

(2)

(3)

式中fj、fe分别为因素j和误差的自由度.Fj越大说明该因素对该指标的影响越大,该因素越重要,也可据此进行重要性排序.若Fj>F1-α(fj,fe),α为置信水平,则认为因素j对该指标有显著影响,否则无显著影响.由此可见,方差法相对于极差法的一大优势在于可以判断因素的显著程度.

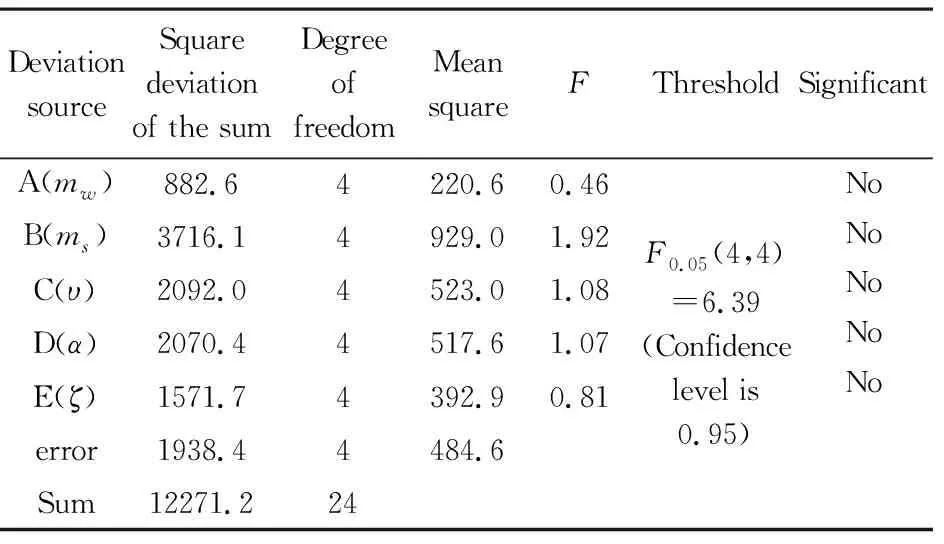
表3 最大展开面积的方差分析Table 3 Variance analysis of maximum deployment area

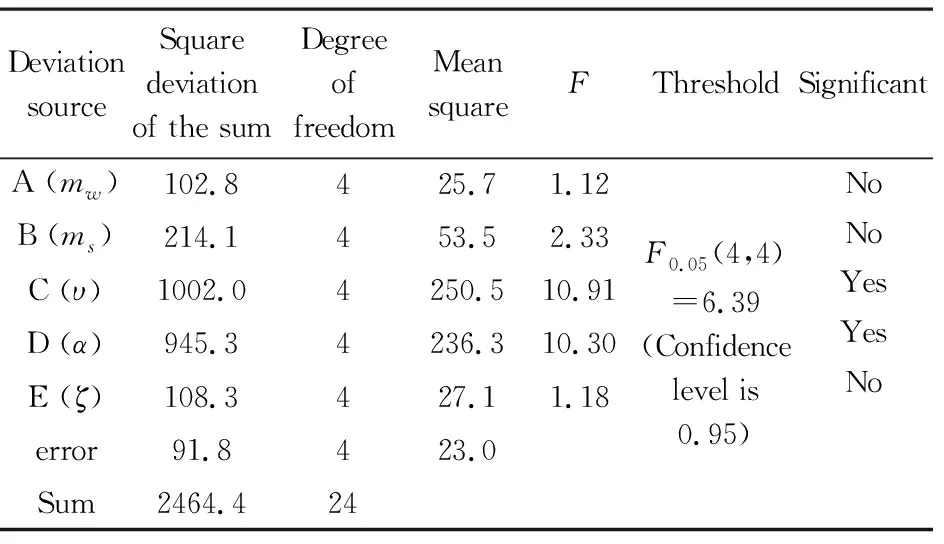
表4 最大展开时间的方差分析Table 4 Variance analysis of maximum deployment time

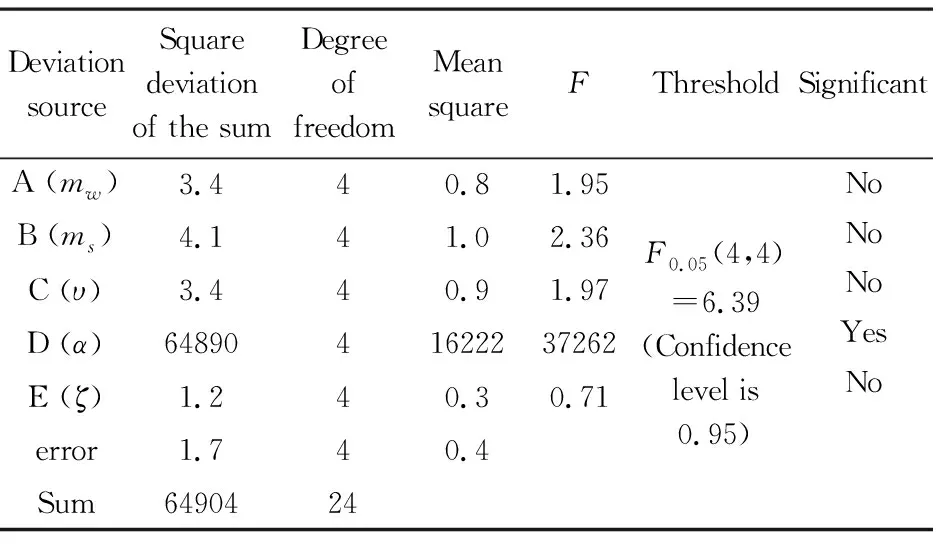
表5 最大展开距离的方差分析Table 5 Variance analysis of maximum deployment distance

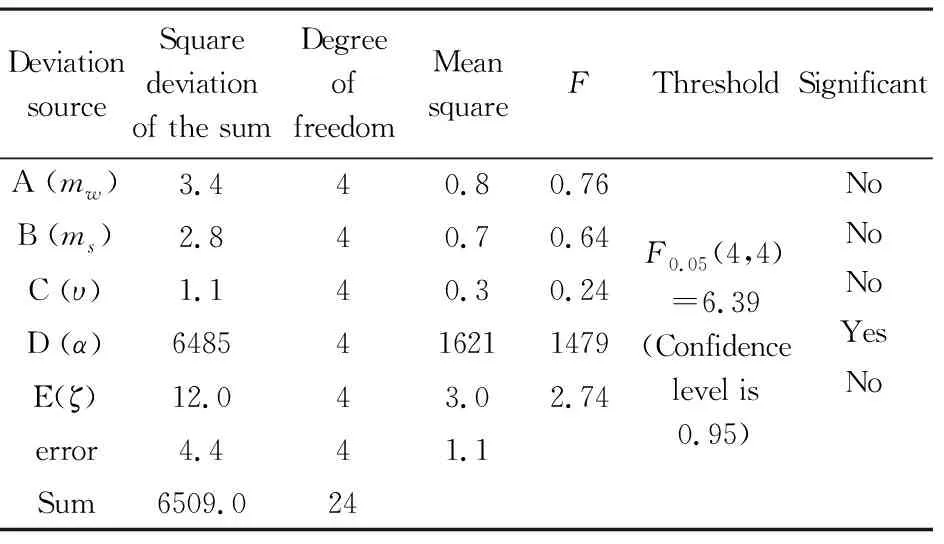
表6 有效作用距离的方差分析Table 6 Variance analysis of effective action distance

4 空间绳网展开参数灵敏度分析

针对表2中的正交试验结果,运用极差法和方差法,分最大展开面积、最大展开时间、最大展开距离和有效作用距离四项指标,依次进行参数灵敏度分析,确定各因素的主次顺序和显著程度等.

4.1 最大展开面积的参数灵敏度分析

最大展开面积的极差分析与方差分析的结果如表7、表3所示,各因素不同水平下的最大展开面积的变化规律如图4所示.可以看出,对最大展开面积的影响中,5个因素的重要程度为ms>υ>α>ζ>mw,然而在0.95的置信水平下,各个因素对最大展开面积都不显著.还可看出,在不同因素的不同水平下,最大展开面积的数值都大于设计值的80%(1280m2),这说明在所有给定的试验条件下,空间绳网都能有效展开.另外,最大展开面积的相对变化很小,其数值基本在1557～1591m2之间,这也说明了最大展开面积对这些因素都不敏感.

表7 最大展开面积的极差分析表Table 7 Range analysis of maximum deployment area

图4 各因素不同水平下的最大展开面积Fig.4 Maximum deployment areas in various levels of every factor

4.2 最大展开时间的参数灵敏度分析

最大展开时间的极差分析与方差分析的结果如表8、表4所示,各因素不同水平下的最大展开时间的变化规律如图5所示.可以看出,对最大展开时间的影响中,5个因素的重要程度为υ>α>ms>ζ>mw,其中υ和α为显著性因素,ms、ζ和mw无显著性影响.由图5还可看出,随着υ和α的增大,最大展开时间都不断减小.

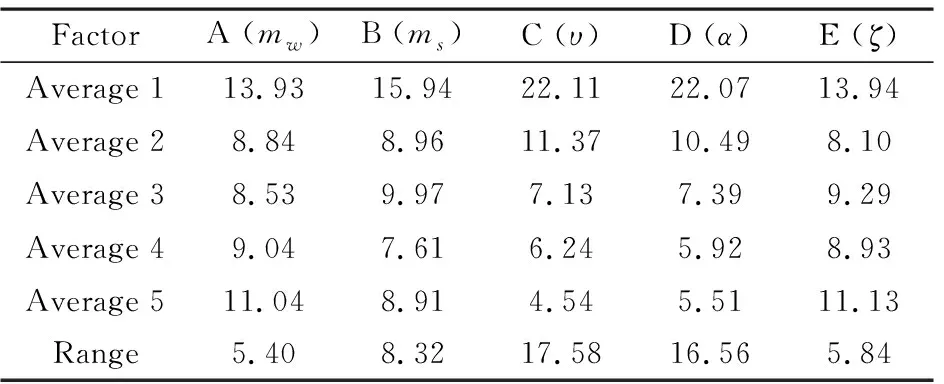
表8 最大展开时间的极差分析Table 8 Range analysis of maximum deployment time

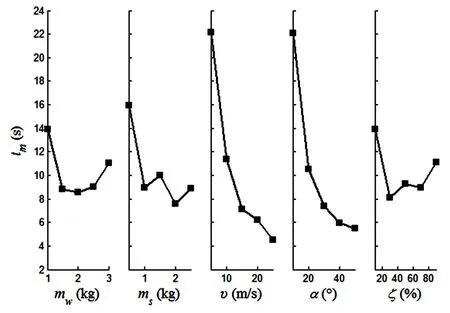
图5 各因素不同水平下的最大展开时间Fig.5 Maximum deployment times in various levels of every factor

4.3 最大展开距离的参数灵敏度分析

最大展开距离的极差分析与方差分析的结果如表9、表5所示,各因素不同水平下的最大展开距离的变化规律如图6所示.可以看出,对最大展开距离的影响中,5个因素的重要程度为α>ms>υ>mw>ζ,其中α为显著性因素,ms、υ、mw和ζ无显著性影响.由图6还可看出,随着α的增大,最大展开距离有不断减小的趋势.

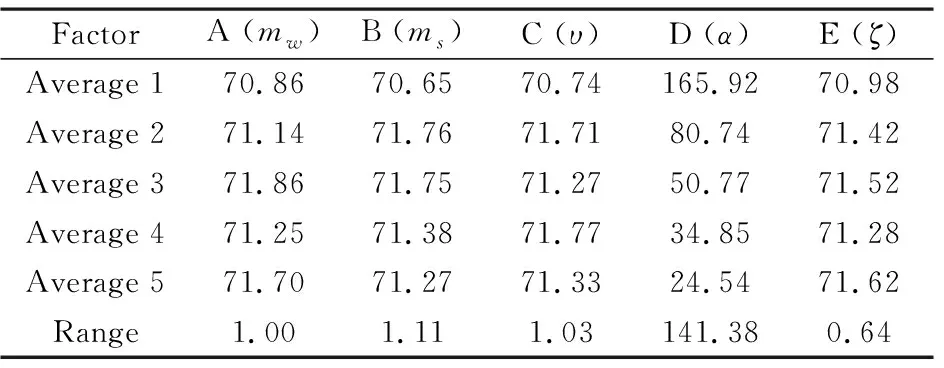
表9 最大展开距离的极差分析Table 9 Range analysis of maximum deployment distance

4.4 有效作用距离的参数灵敏度分析

有效作用距离的极差分析与方差分析的结果如表10、表6所示,各因素不同水平下的有效作用距离的变化规律如图7所示.可以看出,对有效作用距离的影响中,5个因素的重要程度为α>ζ>mw>ms>υ,其中α为显著性因素,ζ、mw、ms和υ无显著性影响.由图7还可看出,随着α的增大,有效作用距离有不断减小的趋势.

图6 各因素不同水平下的最大展开距离Fig.6 Maximum deployment distances in various levels of every factor

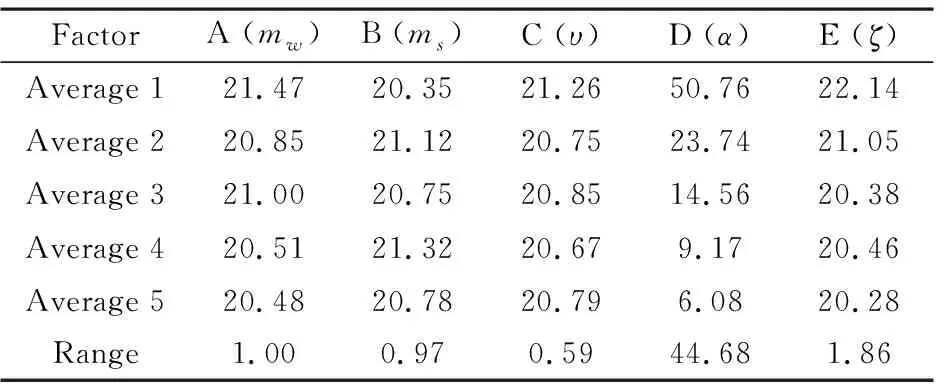
表10 有效作用距离的极差分析Table 10 Range analysis of effective action distances

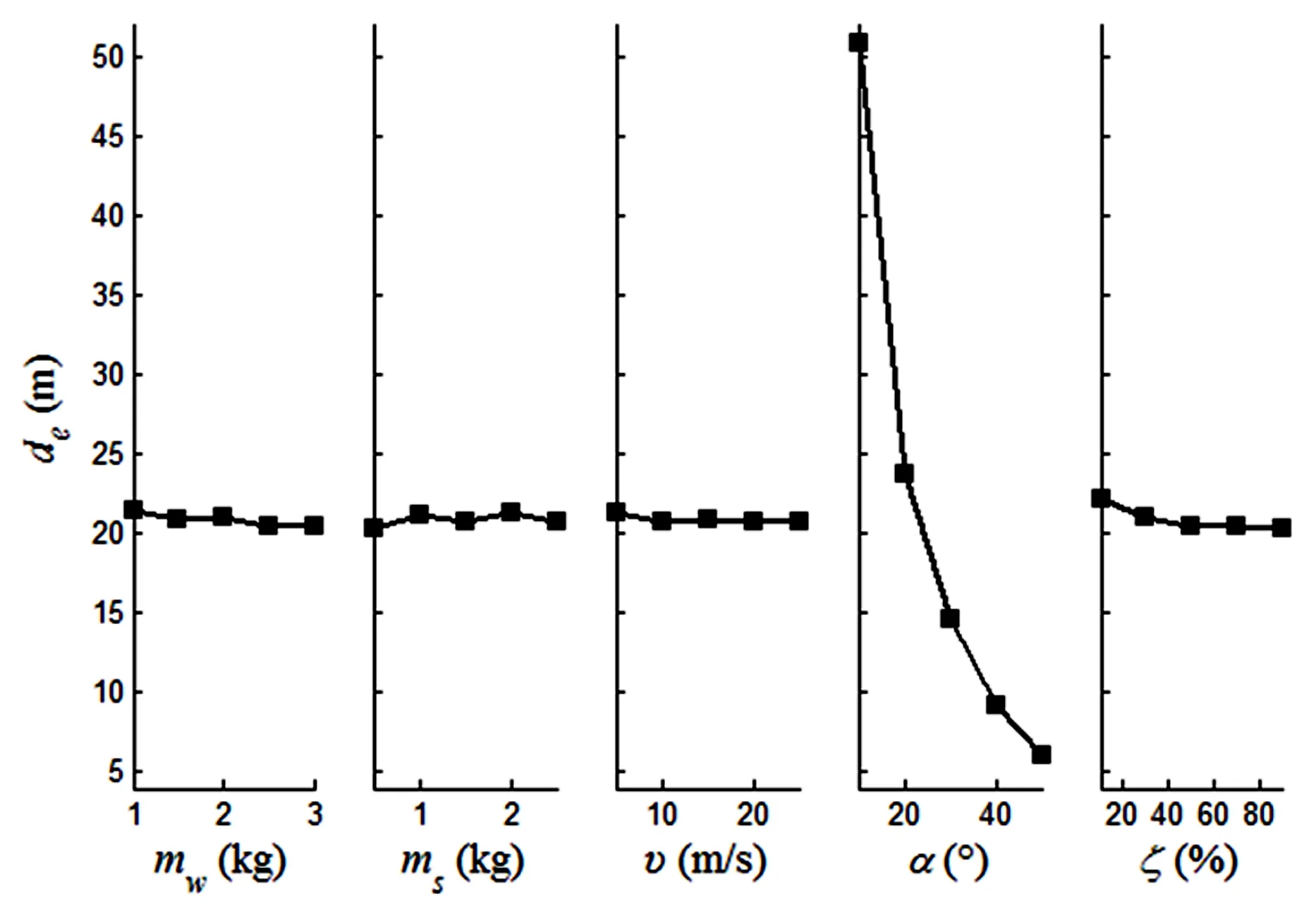
图7 各因素不同水平下的有效作用距离Fig.7 Effective action distances in various levels of every factor

5 指标间相关性分析

通过对比图6与图7可以发现,最大展开距离dm与有效作用距离de这两个性能指标受各因素的影响规律基本相似,也就是说这两个指标可能存在较强的相关关系.为了进一步考察所有指标的相关关系,下面进行指标间相关性分析.

求出各指标间相关系数如表11所示,同时为了能更直观显示指标间相关性,绘制各指标间相关性散点图如图8所示.可以看出,在指标自相关之外,不同指标间的相关性中:dm与de高度相关,相关系数为0.9985,两者的散点图也几乎成一条直线；tm与dm、tm与de中等相关,相关系数为分别为0.5769与0.5603；Sm与其它指标相关性都较为微弱.

表11 各指标间相关系数Table 11 Correlation coefficients between the indicators

图8 各指标间相关性散点图Fig.8 Scatter plot of the correlationship between the indicators

6 小结

本文基于正交试验对影响空间绳网展开效果的设计参数进行了灵敏度分析,通过研究得出以下基本结论:

(1)在所有给定的试验条件下,空间绳网都能有效展开,而且所有考察的设计参数都对最大展开面积无显著性影响,因此在下一步参数优化设计中,可不再将最大展开面积作为待优化性能指标.

(2)绳网质量、质量块质量与绳索阻尼比这三个设计参数对本文所考察的所有性能指标都无显著性影响,为简便起见,可在下一步参数优化设计中剔除这三个设计参数,直接取为常量.

(3)最大展开距离与有效作用距离高度正相关,而且工程设计中希望这两个指标都尽量大,因此当两者之一的指标达到最优时,另一个也基本为最优,于是在下一步参数优化设计可只选两者之一作为待优化的性能指标.

于是,本文通过空间绳网展开参数灵敏度分析,确定了各设计参数的主次顺序和显著程度,剔除了低灵敏度的参数；同时为下一步的空间绳网展开参数优化设计,精简了待优化性能指标的个数.

1陈钦. 空间绳网系统设计与动力学研究[博士学位论文]. 长沙:国防科学技术大学, 2010 (Chen Q. Design and dynamics of an orbital net-capture system[Ph.D Thesis]. Changsha:National University of Defense Technology, 2010 (in Chinese))

2Zhai G, Qiu Y, Liang B, et al. On-orbit capture with flexible tether-net system.ActaAstronautica, 2009,65(5-6):613～623

3刘海涛. 空间绳网展开及复合体离轨动力学与控制[博士学位论文]. 长沙:国防科学技术大学, 2014 (Liu H T. Dynamics and control of space net deployment and combination reorbiting[Ph.D Thesis]. Changsha:National University of Defense Technology, 2014 (in Chinese))

4陈钦,杨乐平. 空间绳网系统发射动力学问题研究. 宇航学报, 2009,30(5):1829～1833 (Chen Q, Yang L P. Research on casting dynamics of orbital net systems.JournalofAstronautics, 2009,30(5):1829～1833 (in Chinese))

5李京阳,于洋,宝音贺西. 空间飞网系统抛射参数优化研究. 宇航学报, 2012,33(6):823～829 (Li J Y, Yu Y, Baoyin H X. Simulation and comparison of different dynamical models of space webs.JournalofAstronautics, 2012,33(6):823～829 (in Chinese))

6邱清盈,冯培恩. 基于正交试验的灵敏度分析法. 机械设计与制造, 1997(5):4～7 (Qiu Q Y, Feng P E. A method of sensitivity analysis based on orthogonal test.JournalofMachineDesign, 1997(5):4～7 (in Chinese))

7李云雁,胡传荣. 试验设计与数据处理. 北京:化学工业出版社, 2008 (Li Y Y, Hu C R. Experiment design and data processing. Beijing:Chemical Industry Press, 2008 (in Chinese))

8陈魁. 试验设计与分析. 北京:清华大学出版社, 2015 (Chen K. Design and analysis of experiments. Beijing:Tsinghua University Press, 2015 (in Chinese))

9张武,陈剑,陈鸣. 采用正交试验的发动机悬置系统灵敏度分析. 噪声与振动控制, 2011(5):168～172 (Zhang W, Chen J, Chen M. Sensitivity analysis of engine′s mounting system based on orthogonal experiments.NoiseandVibrationControl, 2011(5):168～172 (in Chinese))

10 闫晓东,韩冰. 试验设计方法在飞行器性能仿真验证中的应用. 飞行力学, 2012,30(1):79～82 (Yan X D, Han B. Application of experiment design method in performance simulation validation for flight vehicle.FlightDynamics, 2012,30(1):79～82 (in Chinese))

11 王志伟,樊文欣,赵俊生等. 基于二次回归正交试验的强力旋压连杆衬套性能分析. 锻压技术, 2014,39(1):69～73 (Wang Z W, Fan W X, Zhao J S, et al. Performance analysis of power spinning connecting rod bushing based on quadratic regression orthogonal test.Forgine&StampingTechnology, 2014,39(1):69～73 (in Chinese))

12 于洋. 空间飞网抛射过程动力学研究[博士学位论文]. 北京:北京航空航天大学, 2009 (Yu Y. Deployment dynamics of launched space webs[Ph.D Thesis]. Beijing: Beijing University of Aeronautics and Astronautics, 2009 (in Chinese))

13 刘海涛,张青斌,杨乐平等. 空间绳网系统展开动力学特性分析. 国防科技大学学报, 2015,37(3):68～77 (Liu H T, Zhang Q B, Yang L P, et al. The deployment dynamic characteristics analysis of space web system.JournalofNationalUniversityofDefenseTechnology, 2015,37(3):68～77 (in Chinese))