基于分布式计算的大数据聚类算法预测强度优化研究

郭烨旻

(吉林工程技术师范学院信息工程学院，吉林长春 130052)

大数据聚类算法的应用主要集中在图形处理、模式匹配、市场分析等领域。大数据的聚类分析研究存在着各种困难，而这些困难是由大数据本身的特点所决定的。进入大数据时代后需要处理的数据量规模剧增，使用串行方式进行数据分析的传统聚类方法已经难以适应当前云计算网络环境下的数据处理需求，本研究采用并行的方式，以预测强度为切入点对大数据聚类算法进行研究和优化。

对某一指定的数据集以其一项或几项属性为出发点，对其进行分类的这一过程被称为聚类，而在聚类的过程中并不需要对数据集的全部属性进行充分的了解。一般将所分的多个类别中的每一个称为一个蔟(Cluster)，以数据在一项或几项特定属性上的相似度，作为不同蔟之间的划分标准。所以，在聚类的过程中并不需要预先设置分类标准，而是以数据本身的特定属性为依据，自动进行分类。

1 数据分析系统

当前大数据分析处理系统主要有两大方向：以Hadoop为代表的批处理系统；为特定应用所开发的流处理(Stream Processing)系统。其主要区别在于批处理系统需要储存后再处理，而流处理系统则是直接处理。单一的数据分析处理系统对当前云计算网络环境下数据量剧增的情况难以适应，应用体系结构与底层设计语言混合以及大数据处理高层计算模式混合的混合式数据分析系统更加适应当前的应用需要。

2 预测强度优化的聚类算法

预期中要将数据集划分为蔟的数量是聚类过程中的重要参数，本研究在计算聚类数时使用Tibshirani在2001年提出的基于预测强度的方法。

具体的计算步骤为：

(1)将当前数据集以随机划分的方式分为测试集A和测试集B；

(2)以k作为当前聚类数，对两个子集进行聚类，记录结果；

(3)将两个子集的聚类结果进行判别；

(4)统计集合A所有蔟中的样本在集合B中的分类误差，计算分配的正确率；

(5)以k为聚类数的预测强度为所有正确率中的最小值。

在预测强度定义中，C(A,k)表示将集合A聚为k类，Akj表示集合B聚成的第j类，nkj代表Akj中的元素数量，D[C(A,k),B]ii′为聚类结果判别矩阵中i行i′列的元素值。由此可见，预测强度值pk(s)∈[0,1]，受聚类数影响。预测强度值越大，说明当前聚类算法能够将新数据元素划分到正确的蔟的预测能力越强。

预测集合和测试集合对数据的随机划分，会导致预测强度受到偶然因素干扰比较严重。本文提出将数据先行划分成多个随机类，分别作为测试集计算预测强度，取多个预测强度的平均值作为当前聚类数下的最终预测强度，从而减小偶然因素对预测强度的干扰，起到优化算法的作用。

通过预测强度确定聚类数k，从而进行聚类的对应算法如下：

输入：数据集D={d1,d2,…,di,…,dn}，当前最佳聚类数k

(1)从D集合中选取k个属于D的数据点d1′,…,dk′作为聚类后的蔟的质心；

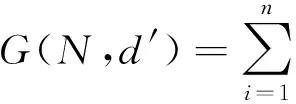
(5)循环运行步骤(2)和步骤(3)，直到(4)的值不再变化，显而易见，准则函数值是在不断缩小的。

其中，Nj应为距数据di最近的质心dj′所在的蔟，sign(Nj=j)表示当Nj=j时其值为1，其他所有情况其值为0。

输出：质心d1′,…,dk′所在的蔟N1,…,Nk

取某直播平台访客在不同栏目上停留时间的数据，输入三个栏目的数据，以主播数量3作为变量数进行分析。选用BIC准则建立模型，生成变量数与聚类数之间的函数曲线，对比优化后的基于预测强度的变量数与聚类数关系函数曲线如图1所示。

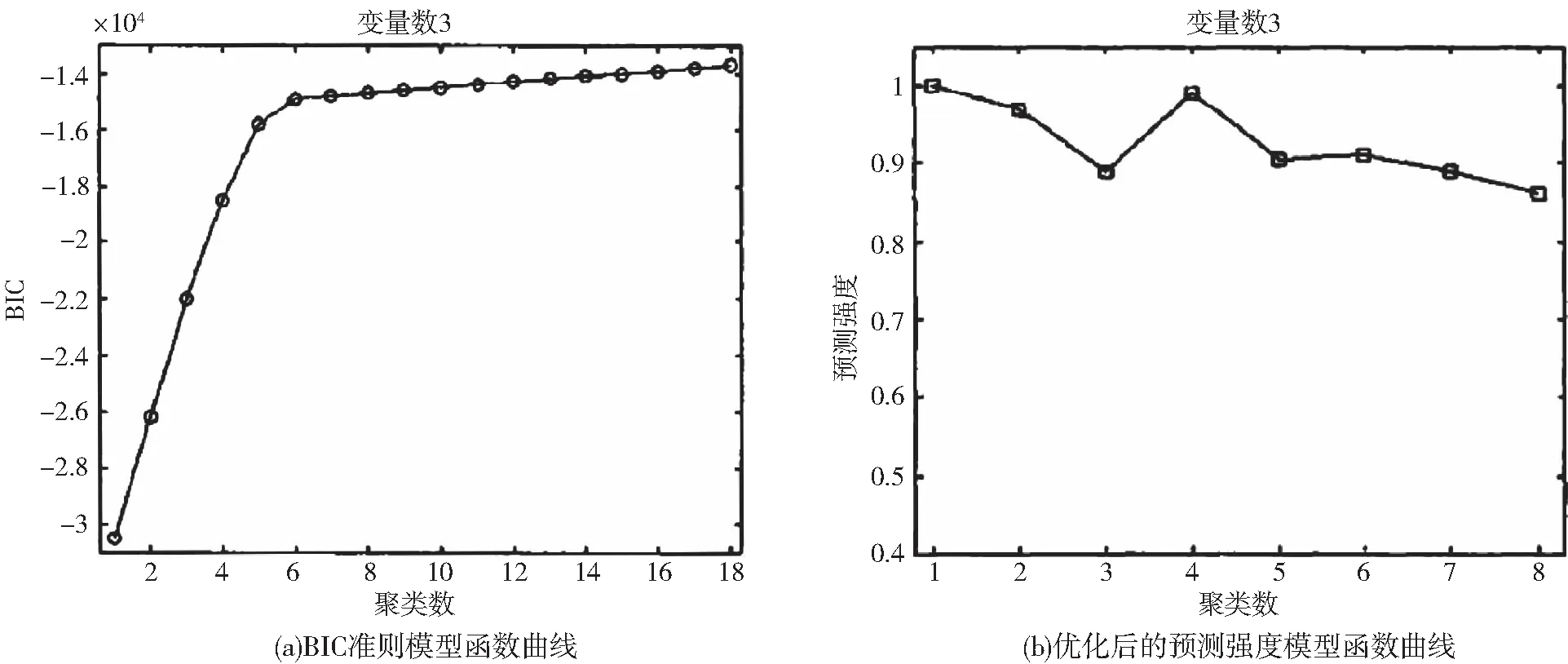
图1 优化后算法与已有算法对比图

在相同变量数的条件下，BIC准则本身对聚类数的确定没有影响，从使用BIC准则的图1中可看出，当聚类数超过4之后图像趋于平稳，受偶然因素干扰程度较小，聚类数应为超过4的值，但无法完全确定具体取值。而使用优化后的算法可得到聚类数为4时预测强度有最大值，能够较为准确地确定聚类数。

按照测试强度确定聚类数为4，聚类分析后的曲线如图2所示。

通过对图2的分析可以明显看出，具有第一类属性的访客对大部分栏目都有较大的兴趣，他们所具有的属性与平台的栏目设置方向一致性较大，对该属性用户的服务可以做适当的倾斜。而第四类用户明显对平台当前的内容兴趣欠缺，在没有开设新栏目之前可以对具有第四类属性的用户适当忽略。

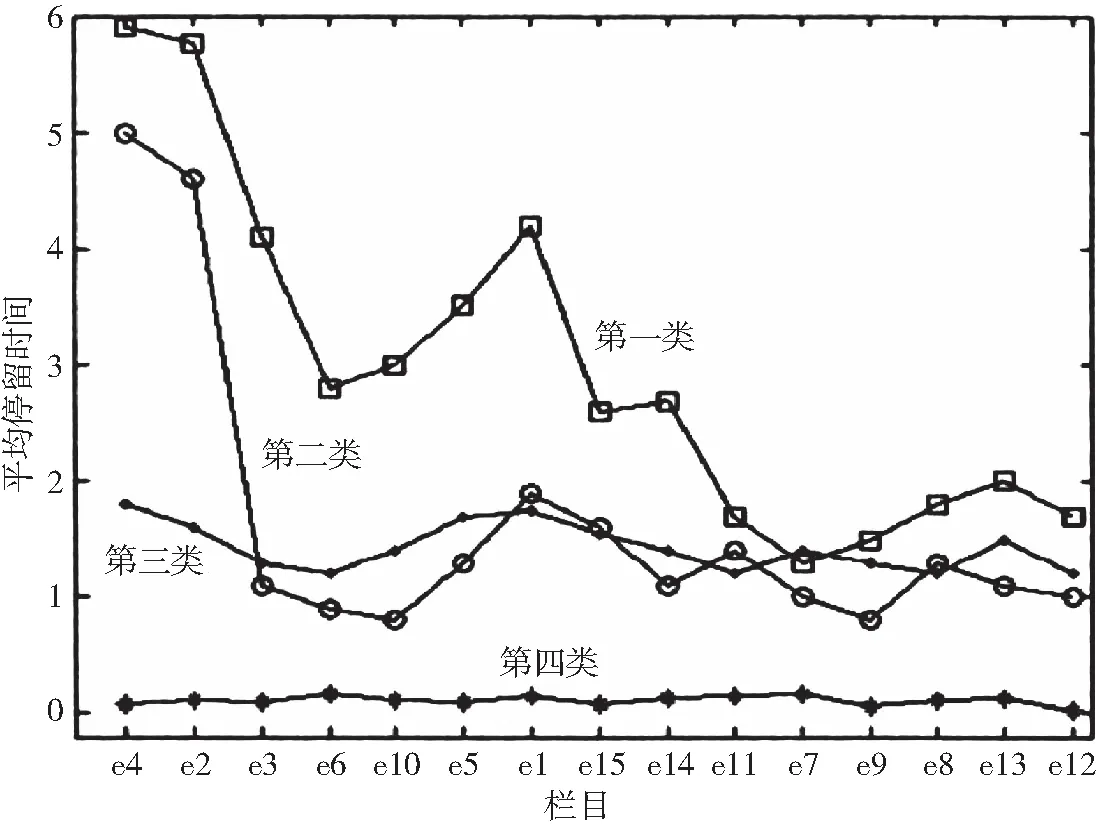
图2 不同类访客在所有栏目上的平均停留时间

3 结语

通过以上测试可以看到优化后的聚类算法在实际应用中的作用。以传统聚类算法为基础，对确定具体聚类数量的方法进行适当的优化，可以有效地减少偶然因素对聚类结果的干扰，使用该算法在进行大量数据聚类分析时能够有效地减少时间复杂度以及经济支出，具有一定的应用价值。

[参考文献]

[1]李国杰,程学旗.大数据研究:未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考[J].网络新媒体技术,2012(6):647-657.

[2]黄宜华.深入理解大数据:大数据处理与编程实践[M].北京:机械工业出版社,2014.

[3]杨彦侃.并行的聚类算法研究[D].包头:内蒙古科技大学,2010.

[4]R Tibshirani,G Walther.Cluster Validation by Predication Strength[J].Journal of Computational & Graphical Statistics,2005(3):511-528.