基于Lévy飞行的风驱动优化算法

张 超

(宿州职业技术学院计算机信息系，安徽宿州 234101)

空气相对于地面的运动称为风，风驱动优化算法[1](Wind Driven Optimization，WDO)是对空气质点受力运动达到气压平衡的状态进行模拟，推导出算法的速度更新计算方式。与其他智能算法相比，WDO算法的速度更新方程是从物理学公式推导而来，包含了各种自然界中真实存在的力对速度的影响，具有实际物理意义，其具有较强的全局搜索能力和较快的收敛速度[2]，已被成功应用于机器人未知静态和动态环境路径规划[3]、锅炉NO_x排放模型优化[4]、各种电磁学问题优化[5-7]等领域。

WDO算法对参数取值敏感，涉及4个参数：RT系数、g(重力加速度常数)、a(摩擦力系数)、c(科里奥利力系数)彼此紧密联系相互耦合，不同的取值组合对算法性能影响较大且不易确定；在算法迭代后期易陷入局部极值，导致算法“早熟”，使种群失去多样性。鉴于此，国内外学者对WDO算法进行了优化和改进研究。Bayraktar Z[8]借助CMAES算法(Covariance Matrix Adaptation Evaluation Strategy，CMAES)的自适应评价策略确定WDO算法的参数取值，有效地提升了通过人工试探确定参数的效率。Javaid N[9]等将遗传算法和风驱动算法混合，使用遗传算法的交叉变异操作替换风驱动算法的速度更新步骤，解决因更新速度过大而导致的算法性能下降问题。Boulesnane A[10]根据大气层中真实存在的低压区和高压区划分不同区域，采取有效避碰措施防止种群之间的冲突，实现了一种适应动态环境优化的风驱动优化算法。

鉴于WDO算法存在的缺陷，本文旨在增强算法的寻优性能。维护种群多样性是提升群智能算法性能的有效策略，而变异操作是群智能算法中群体多样性产生的重要机制之一。为此，本文实现了基于Lévy飞行变异的风驱动算法(Wind driven optimization algorithm with Lévy Flight，LWDO)，针对10个经典测试函数做仿真实验，实验结果表明，LWDO算法的寻优性能较传统WDO算法及相关对比算法有提升，从而验证了改进策略的有效性。

1 风驱动优化算法

风驱动优化算法，使用牛顿第二运动定律和理想气体状态方程，作为算法速度更新方式推导的主要理论依据，其方程如下：

(1)

P=ρRT.

(2)

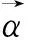
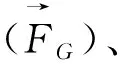
(3)

(4)

(5)

(6)

(7)

为了简化模型便于公式推导，WDO算法令δV=1，假定Δt=1，得到：

(8)

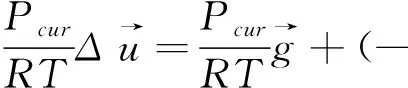
(9)

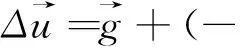
(10)

(11)

(12)

综上所述，(12)式即为WDO算法的空气质点的速度更新方式。(12)式右边包含的4项，分别代表了摩擦力、重力、气压梯度力和科里奥利力对空气质点速度的影响。对于(12)式中包含的4个算法参数：a(摩擦力系数)、g(重力加速度常数)、RT系数和c(科里奥利力系数)，Bayraktar Z[11]在数值实验的基础上，给出了推荐取值范围，一般地，a取[0.8,0.9]，g取[0.6,0.7]，RT取[1.0,2.0]，c取[0.05,3.6]。

WDO算法的位置更新方式通过(13)式计算：

(13)

(14)

2 基于Lévy飞行的风驱动优化算法

2.1 Lévy飞行

Lévy飞行是特殊的随机游走模式，是一种马尔科夫过程，它行走的随机步长服从于一个重尾的Lévy分布。Lévy分布一般用一个简单的幂律公式表示：

(15)

其中，s为随机步长，β为指数参数。Lévy飞行在未知的大规模空间搜索时，比布朗随机运动更加有效，原因之一是Lévy飞行拥有快速增长的无限方差，它比布朗随机运动的方差增长得更快[12]。(16)式和(17)式分别为Lévy飞行和布朗随机运动的方差增长表示形式。

σ2(s)～s3-β，1<β≤2.

(16)

σ2(s)～s.

(17)

Lévy飞行在搜索过程中，频繁的短距离局部搜索与偶尔较长距离的游走相间，如图1所示。因此，在搜索到最优解附近时，能够加速局部搜索，而少数较长距离跳跃式游走，有利于拓展搜索范围，使之更易逃离局部极值的束缚。研究表明，自然界中很多生物的运动轨迹都具有Lévy飞行特征[13]。Lévy飞行已被成功应用于粒子群优化算法、布谷鸟算法、花授粉算法、萤火虫算法等智能优化算法中，并且效果良好[14]。

图1 100次的二维Lévy飞行轨迹(从原点(0,0)开始，标记为□)

在文献[15]中，Lévy飞行的随机步长s，计算公式如下：

(18)

其中，u和v由(19)式正态分布获得：

(19)

其中，

(20)

2.2 LWDO算法

2.2.1 LWDO算法思想

WDO算法在迭代搜索过程中，易受到局部极值的干扰，使算法出现“早熟”现象，导致种群的多样性丧失，算法进化陷入停滞。增加变异机制是维护种群多样性的有效策略，通过变异操作能够增加算法获得新的候选解机会，有助于算法跳出当前局部极值陷阱，保障算法正常进化，获得全局最优解。鉴于Lévy飞行的频繁短距离局部搜索特性，当搜索到最优解附近时，能够增强、加速局部搜索速度。为此，本文提出一种基于Lévy飞行变异的风驱动优化改进算法LWDO，LWDO算法通过设置一个变异参数P∈[0,1]控制空气质点变异，如果随机产生一个随机数小于等于P，那么该空气质点将被选择发生变异，变异的空气质点使用公式(21)进行位置更新计算。

(21)

其中，xi为被选择空气质点变异后的新位置，Levy(s)为Lévy分布，xopt为到目前位置最优空气质点位置。式(21)将到目前为止最优空气质点位置，通过Lévy飞行变异后赋予被选择变异的空气质点，一是充分利用了种群中最优个体的优势信息；二是通过Lévy飞行对最优空气质点附近的搜索空间进行频繁局部搜索，加快了局部搜索的收敛速度；三是伴随Lévy飞行的少数较长距离跳跃式游走，又能使算法跳出局部机制的束缚，搜索到更大空间，提升了算法收敛到全局最优解的概率。

2.2.2 LWDO算法流程

LWDO算法的执行流程如图2所示。

图2 LWDO算法流程

3 仿真实验与性能分析

3.1 实验设计与测试函数

为了验证LWDO算法的寻优性能，本节使用10个经典测试函数进行仿真实验，其中包括单峰函数、多峰函数和旋转函数，函数具体信息见表1，表1中f9、f10两个旋转函数的旋转方法具体可参见文献[16]。

本节实验着重比较LWDO算法与传统WDO算法、改进AWDO算法及其将2.2.1节(21)式中Lévy分布变异替换为高斯分布变异的风驱动改进算法，为比较方便，记为GWDO。与粒子群算法(Particle Swarm Optimization，PSO)、花授粉算法(Flower Pollination Algorithm，FPA)、遗传算法(Genetic Algorithm，GA)等经典和新兴的智能算法进行比较。

算法的参数设置：7种算法的种群规模设为n=30，最大迭代次数T=200，函数维度d=30。LWDO、WDO和GWDO算法的a=0.8，g=0.7，RT=1.0，c=0.7，maxV=0.3。PSO的学习因子c1=c2=2，最大速度为搜索空间的一半。GA的交叉概率为0.9，变异概率为0.08。FPA算法的p=0.2，γ=16。

表1 测试函数

3.2 实验结果和性能分析

算法性能评价使用50次实验的平均值和标准差两个指标，实验结果见表2。可以看出，在f1、f2和f3三个单峰函数上，LWDO算法和传统WDO算法及其改进算法AWDO、GWDO一样，都能收敛到函数的理论极值，优于PSO、GA和FPA三种智能算法。在f4函数上，LWDO算法的寻优性能略优于其他6种对比算法。

在f5、f6、f7、f8四个多峰函数上，LWDO算法的平均值和标准差均为0，说明LWDO算法50次仿真实验均能收敛到四个函数的理论极值，寻优性能较好；WDO、AWDO、GWDO三种算法在f7、f8函数上的平均值和标准差均为0，说明与LWDO算法一样，50次仿真实验均能收敛到这两个函数的理论极值，也优于PSO、GA和FPA三种智能算法；而在f5、f6函数上WDO、AWDO、GWDO三种算法的寻优性能不如LWDO算法，在f5函数上WDO、AWDO、GWDO三种算法的寻优性能也明显低于PSO算法，寻优性能不高。

在f9、f10两个旋转函数上，LWDO算法的平均值和标准差均为0，说明50次实验均能收敛到函数的理论极值，寻优性能明显优于其他6种对比算法。

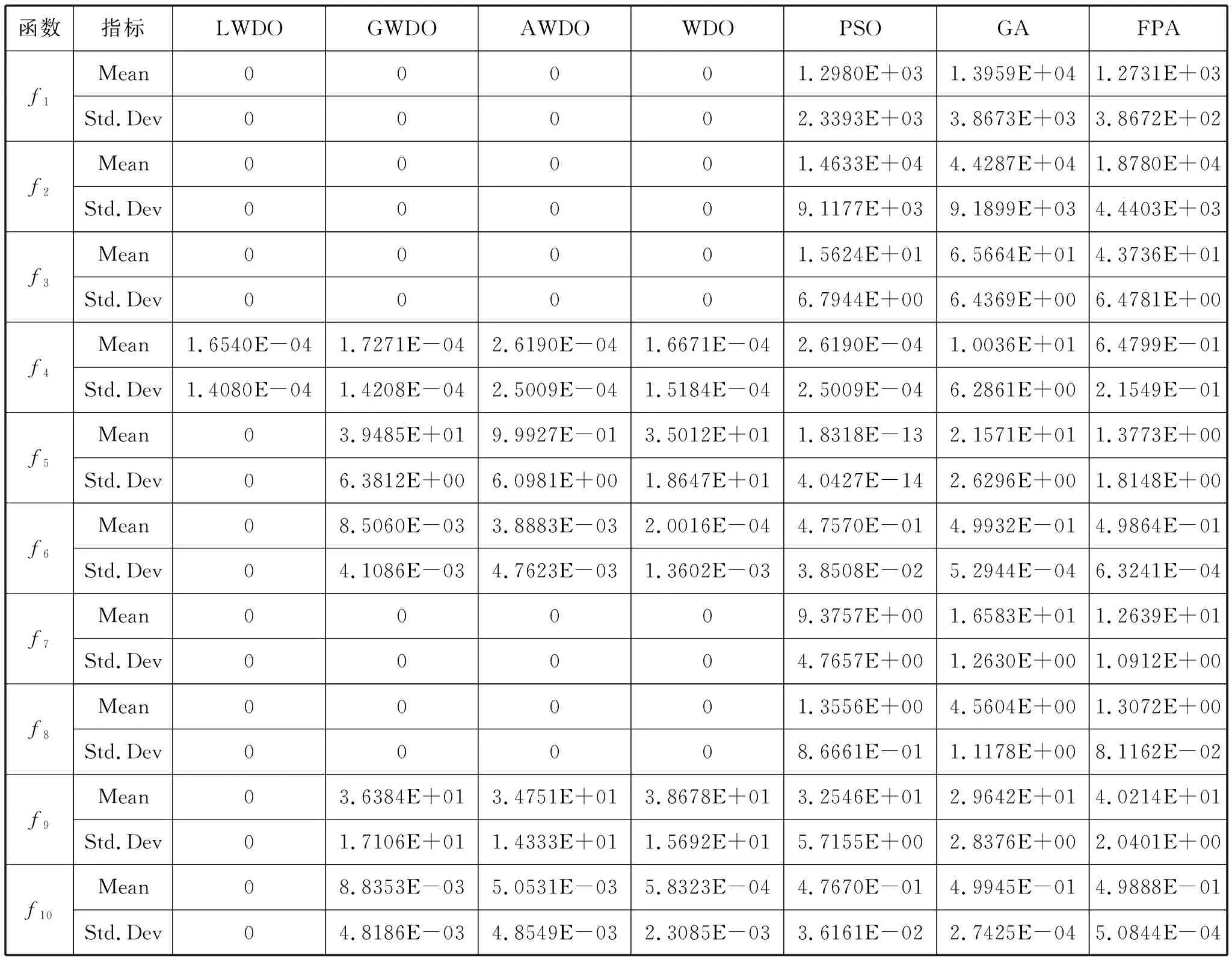
表2 实验结果

图3为7种算法在测试函数上的适应度值收敛曲线(适应度值做10为底的对数处理)。由图3可以看出，LWDO算法在除了f4的其他9个函数上，收敛曲线出现间断，说明LWDO算法已收敛到函数的理论极值0，对数真数为0时曲线不显示，并且算法收敛到函数最优值的速度显著快于其他6种对比算法；对于f4函数，LWDO算法虽未能收敛到函数的理论极值，但从适应度的收敛曲线看，也优于对比算法。

高斯变异是智能算法优化中最常使用的增强局部搜索的方法，从图3亦可获知，使用了高斯变异的GWDO算法，在f1、f2、f3、f7、f8五个函数上，收敛到函数最优值的速度显著快于WDO、AWDO、PSO、GA和FPA算法，但与使用了Lévy分布变异的LWDO算法比，寻优性能不如LWDO算法，从而说明通过对风驱动优化算法的当前最优解实施Lévy分布扰动，作为被选择变异空气质点的新位置，充分利用了Lévy分布频繁短距离局部搜索的特征，使最优解附近的搜索区域充分被搜索，提升了算法局部搜索的速度，而Lévy分布偶尔长距离搜索的特性又拓展了算法的可行搜索空间，增强了算法跳出局部极值的概率，进而加快了算法收敛到全局最优解的速度。

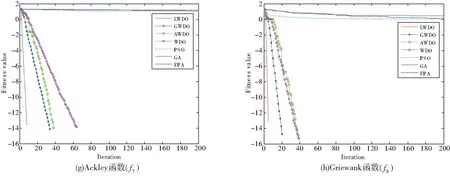
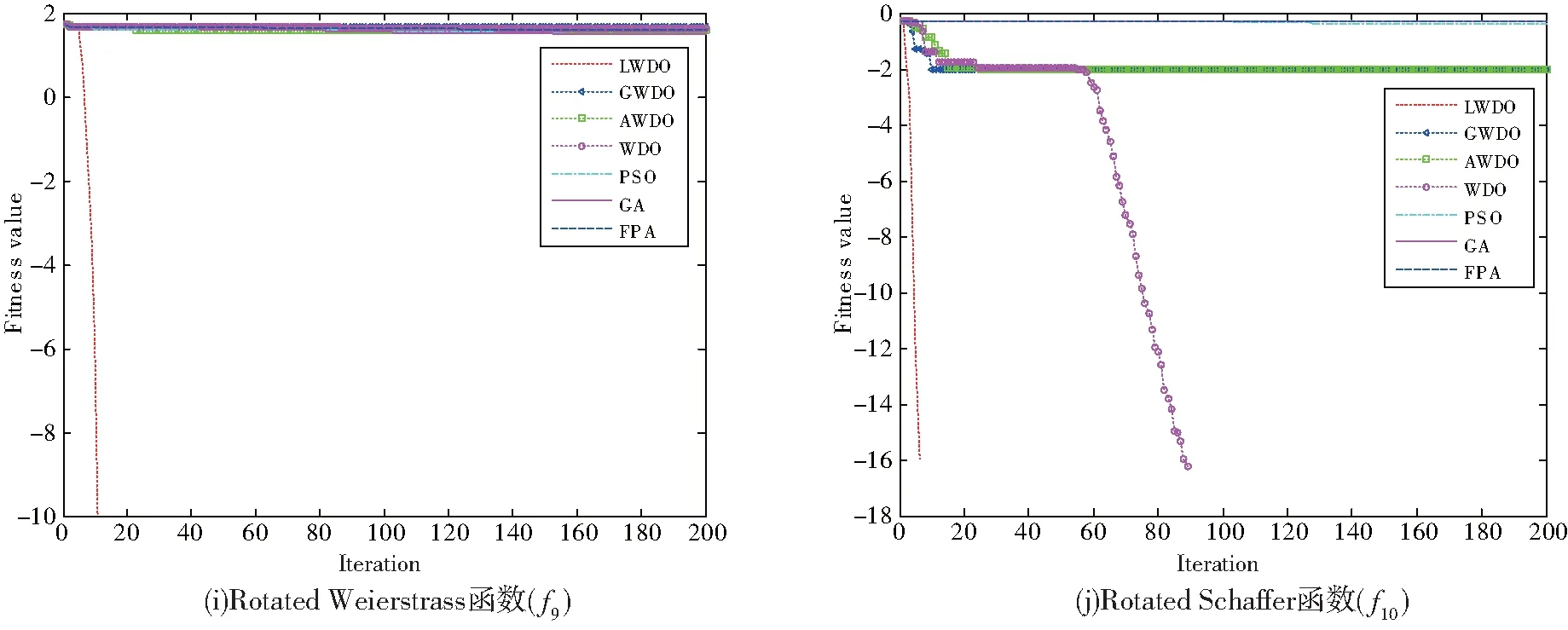
图3 适应度收敛曲线

图4为7种算法针对10个测试函数连续独立进行50次实验的全局最优值方差分析，由图4可以看出，LWDO算法50次实验的最优值分布稳定，特别在f5、f6、f9、f10函数上，比传统的WDO算法和改进的AWDO算法、GWDO算法寻优性能要好。

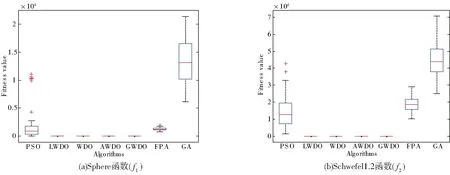
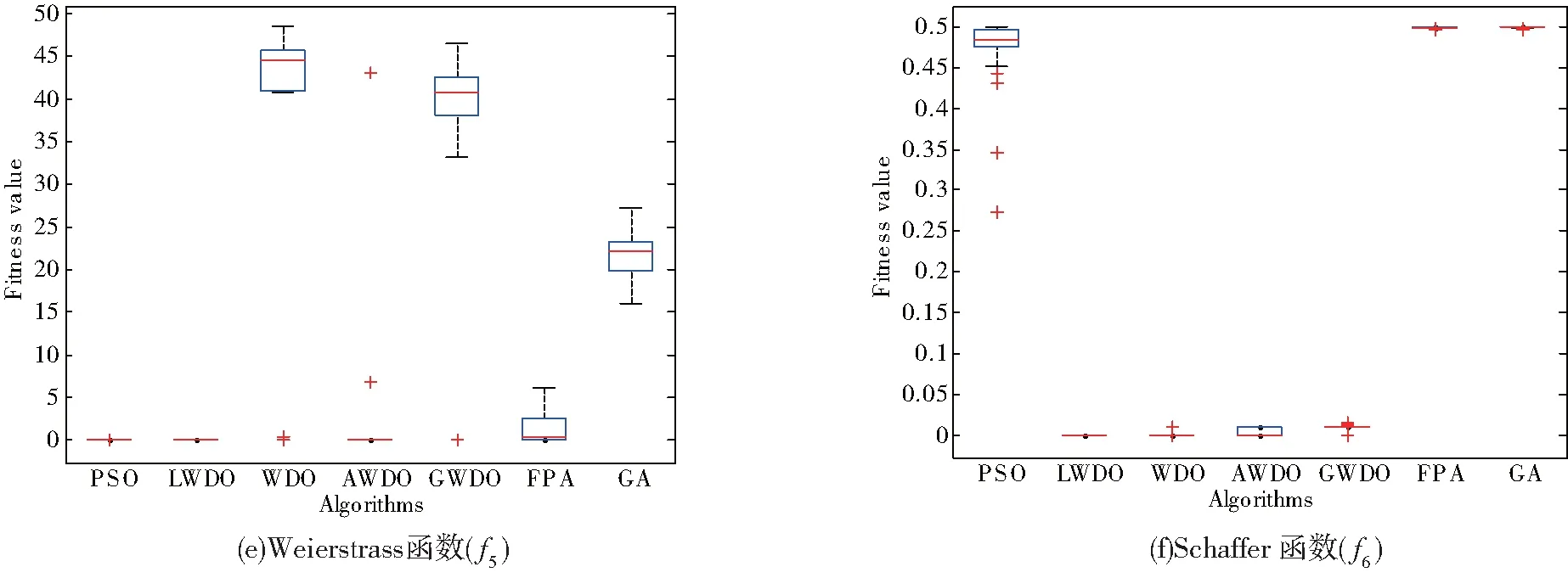
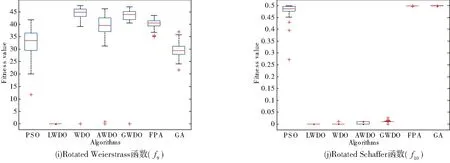
图4 7种算法的全局最优值方差分析

综上所述，LWDO算法在9个函数上的平均值和标准差均为0，在f4函数上的寻优结果也优于其他6种对比算法，因此本文改进的LWDO算法与对比算法相比具有一定竞争性。

4 结语

本文使用Lévy飞行对风驱动优化算法进行了改进。使用10个包括单峰函数、多峰函数和旋转函数在内的测试函数，验证所提改进算法LWDO的性能。LWDO算法在9个函数上，分别独立进行50次实验的结果表明，LWDO算法每次都能够收敛到函数的理论极值，并且所用迭代次数少于对比算法，说明本文提出的改进策略能够加快风驱动优化算法的局部搜索速度，并有效地防止了算法陷入局部极值，比传统风驱动算法的寻优性能有所增强。本文将LWDO算法应用在连续空间的函数优化问题中，下一步我们将继续研究风驱动算法解决离散空间的问题，以及利用LWDO算法解决实际工程应用中比较常见的多目标优化问题。

[参考文献]

[1]Bayraktar Z,Komurcu M,Wemer D H.Wind Driven Optirnization(WDO):A novel nature-inspired optimization algorithm and its application to electromagneties[C].2010 IEEE Antennas and Propagation Society International Symposium (APSURSI),IEEE,2010:1-4.

[2]陈彬彬,曹中清,余胜威.基于风驱动优化算法WDO的PID参数优化[J].计算机工程与应用,2016(14):250-253,260.

[3]Anish Pandey,Dayal R Parhi.Optimum path planning of mobile robot in unknown static and dynamic environments using Fuzzy-Wind Driven Optimization algorithm[J].Defence Technology,2017(1):47-58.

[4]牛培峰,赵振,马云鹏,等.基于风驱动算法的锅炉NO_x排放模型优化[J].动力工程学报,2016(9):732-738.

[5]金雪,夏伟杰,潘彦均,等.基于改进风驱动优化算法的稀疏阵列旁瓣抑制方法[J].数据采集与处理,2017(6):1169-1178.

[6]费晓,张贞凯,田雨波,等.风驱动优化的共享孔径方向图综合[J/OL].电光与控制:1-5[2018-03-20].http://kns.cnki.net/kcms/detail/41.1227.TN.20180314.0920.018.html.

[7]毛晟,张贞凯,田雨波.基于风驱动算法的机会阵雷达波束图综合[J].江苏科技大学学报:自然科学版,2017(4):485-489.

[8]Bayraktar Z,Komurcu M.Adaptive wind driven optimization[C].Eai International Conference on Bio-Inspired Information and Communications Technologies,ICST,2016:124-127.

[9]Javaid N,Javaid S,Abdul W,et al.A Hybrid genetic wind driven heuristic optimization algorithm for demand side management in smart grid[J].Energies,2017(10):1-27.

[10]Boulesnane A,Meshoul S.WD2O:a novel wind driven dynamic optimization approach with effective change detection[J].Applied Intelligence,2017(1):1-17.

[11]Bayraktar Z,Komurcu M,Bossard J A,et al.The wind driven optimization technique and its application in electromagnetics[J].IEEE Transactions on Antennas and Propagation,2013(5):2745-2757.

[12]Yang X S.Nature-Inspired Metaheuristic Algorithms[M].Luniver Press,2008.

[13]朱晓恩,郝欣,夏顺仁.基于Levy flight的特征选择算法[J].浙江大学学报:工学版,2013(4):638-643.

[14]Jamil M.Levy Flights and Global Optimization[M].Swarm Intelligence and Bio-Inspired Computation: Theory and Applications,2013:49-72.

[15]Mantegna RN.Fast,accurate algorithm for numerical simulation of Levy stable stochastic processes[J].Physical Review E,1994(49):4677-4683.

[16]Liang J J,Qin A K,Suganthan P N,et al.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation,2006(3):281-295.