从“随机过程”的角度认识测量误差及其分类

李冰莹， 李永新， 马宇明， 葛方丽

(1.南京理工大学， 江苏 南京 210094； 2.江苏省计量科学研究院， 江苏 南京 210023)

1 引 言

测量是人类认识自然、探索自然必不可少的一种重要手段。由于多种因素的影响，在测量过程中难免存在误差，由测量误差的定义、分类、“随机误差”的分布形式、标准偏差等概念，衍生相应的实用处理方法，形成了测量误差理论体系[1]。

经典误差理论中将误差分为系统误差和随机误差两类不同性质误差。但近年来，在评估误差范围时发现，作为系统误差遗留在测量结果中的误差分量都是不确定的，具有随机性。随着近年来不确定度的推广和应用，人们对测量结果的“测量不确定度”进行评估时，发现作为“系统误差”最终遗留在测量结果中的误差分量，即所谓“未定系统误差”，是不能通过修正消灭的，对“测量不确定度”有不可忽视的贡献。这些所谓“未定系统误差”实际都是不确定的量，也就是通常意义下的“随机量”。因此，经典误差理论中关于“系统误差”和“随机误差”的命名分类需重新认识。

2 经典误差理论中测量误差定义

此处所论测量误差，是指测量仪器(系统、方案)所给出的“测得值”[输出量]与“被测量(的真)值”[输入量]的差值。它包含在对测量仪器(系统)进行“校准”时，由于“校准”方法的不完善(譬如所用测量标准的“不确定”等)所引起的成分，受测量仪器(系统)自身性能结构的不稳定性、被测量的大小及环境条件等影响，是反映测量仪器(系统、方案)综合计量特性的参量。

经典误差理论将正常的测量误差分为系统误差和随机误差两类，以便有效简化“重复测量”时的测量结果处理(测量结果的“测量不确定度”估计；或经典误差理论中的“误差”估计)。

2007年的《国际通用计量学基本术语》(简称《VIM》)第3版对系统误差定义：在重复测量时保持恒定不变或按可预见的方式变化的测量误差分量[2]。其中的“重复测量”可以理解为所论测量仪器(系统、方案)在宏观应用条件相同时(所谓的“重复性测量”条件下)进行的多次测量，包括对同一“工件”的多次测量，也包括对同型号的一批“工件”各测一次而形成的多次测量。定义中的“保持恒定不变”是实际应用中便于辨识、掌握的唯一性客观特征，但“按可预见的方式变化”却千差万别，有所谓的线性系差、周期性系差和复杂规律变化的系差[3]，没有统一的辨识方法可用。

《VIM》第3版对随机误差定义：在重复测量时按不可预见的方式变化的测量误差的分量。该定义与上述“系统误差”相对，以变化方式“不可预见”表明“随机”之名。但定义并未明确“不可预见”的客观标准，对其进行“统计”辨识时便难免带有主观随意性，实际“统计”中往往将“重复测量”时测量误差的所有变化成分都认作“随机误差”分量，这在许多情况下将不能达成对测量误差区分两类的期望效果。

3 测量误差与随机过程

按常规理解，随机的对面应该是确定，因此与随机误差对应的系统误差应该是确定性成分。但其实，到了评估误差范围的阶段，所有的测量误差分量都已被当成随机量看待。测量误差的总体属性或应是“零均值的随机量”，与之对应的时空序列便是所谓的“零均值的随机序列”。

在测量仪器(系统、方案)的工作范围内所进行的任一次测量，都将生成该测量仪器(系统、方案)“测量误差”的一个“样本值”，所有“样本值”构成的序列，便是一个表达该测量仪器(系统、方案)“测量误差”的“随机过程”，并且测量误差作为随机过程具有统计特性。此“随机”的本意是表达其值(各个“样本值”)是不确定的(不能由当前可知的信息确定)，而不是说它在某个考察范围内是否会变化。

“随机过程”的各个元素之间可能“完全无关”，也就是所谓“白噪声”型的“随机过程”，这是一种理想化的“随机过程”； 也可能存在一定的“相关性”，与“白噪声”对应，不妨称之为“有色”的“随机过程”。“有色”的“随机过程”是“随机过程”的一般情形。

虽然“随机过程”属于不能完全掌握其规律的“随机”误差，但“随机过程”中各因素引起的误差分量具有统计规律，可通过自相关函数、概率密度函数、功率谱密度等特性参量分析其特点。

有的误差分量随时间变化非常剧烈，如图1所示ε1(t)，ε1(t)的自相关系数为

(1)

其波形如图1所示γ1(τ)，只在时延τ较小时非零，且ε1(t)的前后取值几乎不相关。

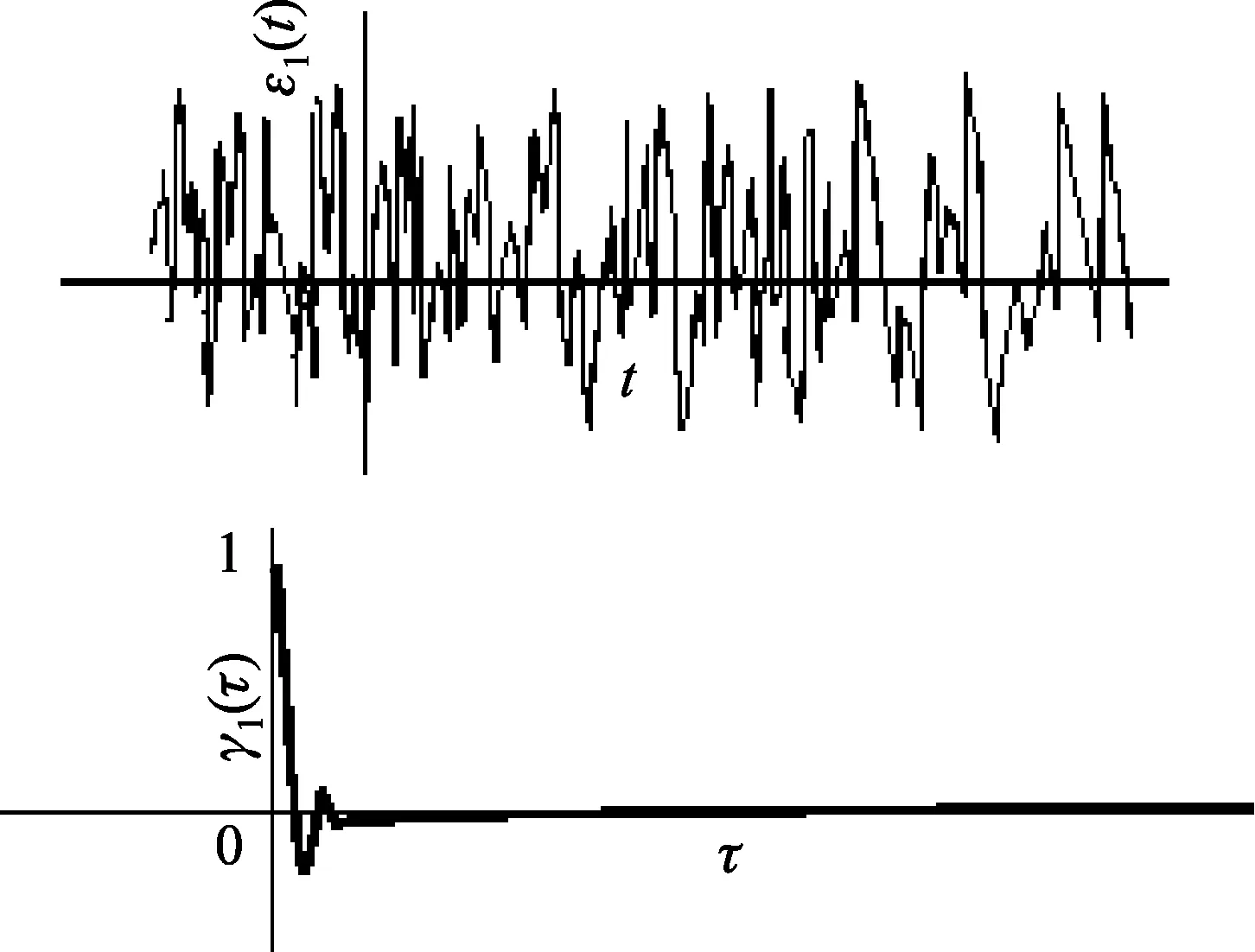
图1 ε1(t)随时间变化示意及其自相关系数γ1(τ)波形

有的误差分量取值随时间变化相对比较缓慢，如图2所示ε2(t)。其自相关系数波形如图2所示γ2(τ)，在较大的时延τ范围内非零，且ε2(t)的前后取值有一定相关性。

图2 ε2(t)随时间变化示意及其自相关系数γ2(τ)波形

有的误差分量则可能在一段相当长的时间内基本不变，只在特定时刻发生跃变，但取值大小是随机、不确定的，如图3所示的ε3(t)。其自相关系数波形如图3所示γ3(τ)，在较大的时延τ范围内接近于1，且ε3(t)的前后取值相关性较大。

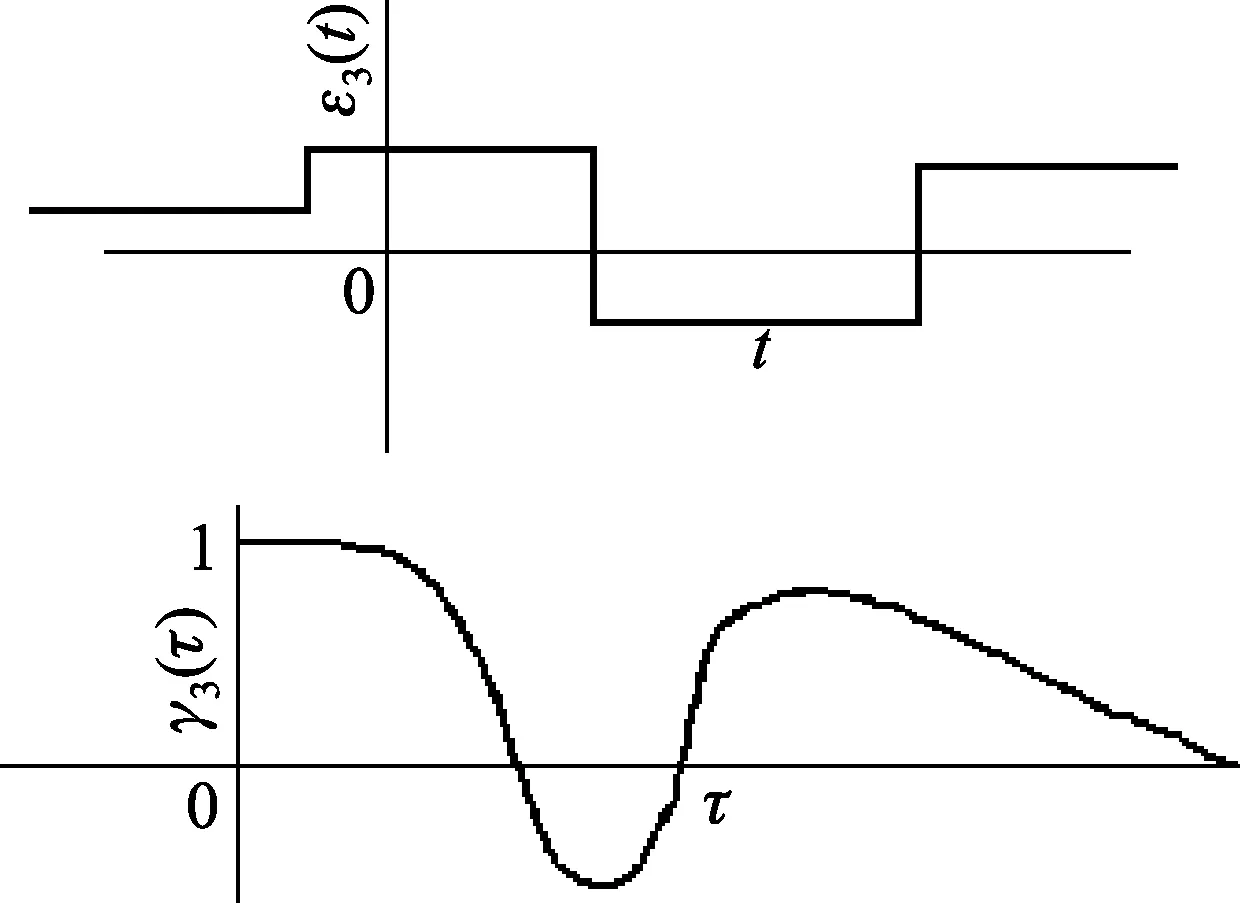
图3 ε3(t)随时间变化示意及其自相关系数γ3(τ)波形

假定某“随机过程”中同时容留上述3个误差分量，即

x*=x+ε1+ε2+ε3

(2)

式中:x*是测量结果；x表示被测量真值。

如果在有限时间内进行m次重复测量，计算m次重复测量结果的平均值，有

(3)

4 系统误差和随机误差新认识

如果对测量仪器(系统、方案)的测量工作不做任何计划安排，完全随机实施测量，大多数因素引起的测量误差分量都可能简化当作“白噪声”型的“随机过程”处理，相应的，对测量误差的“分类”也失去必要。

但测量仪器(系统、方案)的实际测量工作通常并不会随机进行，大多是有计划按步骤进行，其中，“重复性测量”是一种广泛应用的工作模式。在重复性测量条件下，“随机过程”在某个考察范围内是否变化、变化的特征等可根据其测量结果的相关性进行分类。但如果对“随机过程”中各因素引起的测量误差分量都确切求解自相关函数的结果、获取时间关联的定量数据(相关系数的确切值)，不仅工作量巨大，而且实际应用效果也未必理想。

实用的处理方案是将所有“随机过程”分量理想化地分为在时间上完全关联和完全不关联两大类。经典误差理论中系统误差和随机误差之分应是对此“随机过程”的实用分类，其实质是“自相关性”的两种极限情况：系统误差是自相关系数等于1的完全正相关，随机误差是自相关系数等于0的完全不相关。

在时间上前后密切关联的误差分量，其归一化自相关函数的绝对值|γ(τ)|将在较大的时延τ范围内取值接近于1，如图3所示的γ3(τ)。其功率谱密度是如图4所示有色谱G2(f)，误差功率只在一个不太宽的频率范围内相对较大，覆盖的频率范围有限。不妨称之为“有色”误差(colored error)分量εS(t)。

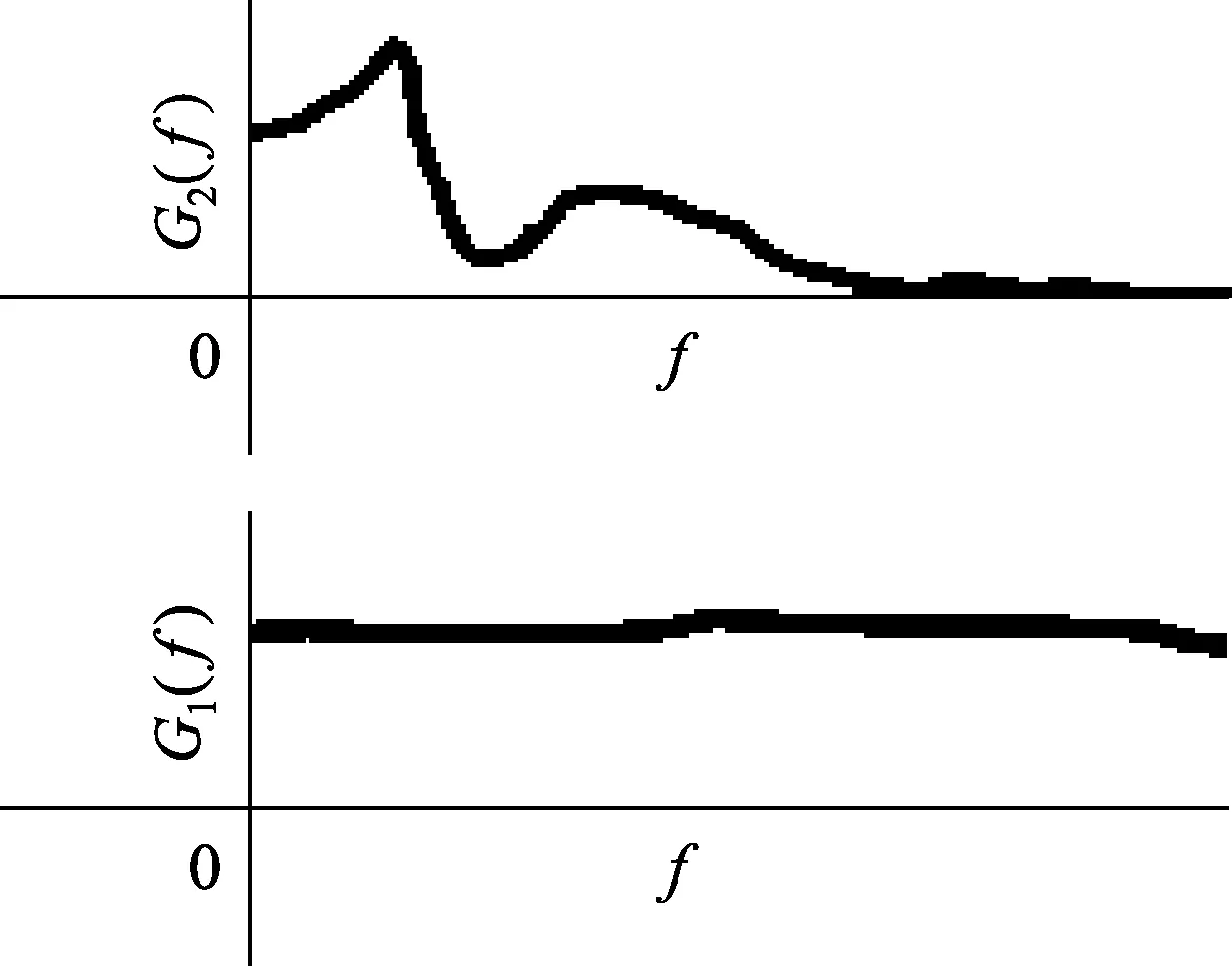
图4 白噪误差、有色误差的功率谱密度

在时间上前后近似完全不关联的误差分量，其自相关函数只在时延τ较小时不等于零，如图1所示的γ1(τ)。其功率谱密度如图4所示G1(f)，近似于“白噪声”，误差功率在较宽的频率范围内近似一致，几乎覆盖全屏。不妨称之为“白”误差(white error)分量εW(t)。

将完整的“随机过程”ε(t)理想化地分为“白”误差εW(t)和“有色”误差εS(t)两大类后，将有

ε(t)=εW(t)+εS(t)

(4)

且εW(t)与εS(t)是互不相关的，与经典误差理论中“测量误差=随机误差+系统误差”一致。

5 结 论

实际上，“系统性的”与“随机性的”并不是两个能够完全划清界限的概念，人为从概念上区分“系统误差”、“随机误差”于误差分析和补偿的实用意义也许并不大。尝试摒弃将经典误差理论中测量误差区分为“系统误差”与“随机误差”的做法，努力探索误差的具体形成规律，找到规律确定、补偿可行的误差分量，加以硬件或软件补偿，对切实提高测量精度实用意义可能更大。

[参考文献]

[1] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2010.

[2] 耿维明. 测量误差的概念及其分类[J].中国计量,2010，(12):68-71.

[3] 肖明耀.误差理论与应用[M].北京:计量出版社,1985.

[4] BIPM,IEC,IFCC,IUPAC,IUPAP,ISO,OIML. Guide to the Expression of Uncertainty in Measurement(GUM)[S]. 1995.

[5] 王立吉.计量学基础[M].北京:中国计量出版社,2006.

[6] 张世箕.测量误差及数据处理[M].北京:科学出版社,1979.

[7] ISO/IEC GUIDE 98-3:Uncertainty in Measurement-Part3: Guide to the Expression of Uncertainty in Measurement)(GUM)[S].2008.

[8] ISO/IEC GUIDE 99:International vocabulary of metrology-Basic and general concepts and associated terms (VIM)[S]. 2007.

[9] 沙定国.实用误差理论与数据处理[M].北京:北京理工大学出版社,1993.

[10] JCGM_200:International vocabulary of metrology-Basic and general concepts and associated terms (VIM 3rd edition)[S].2012.